ESERCITAZIONE_4_Valerio Minella

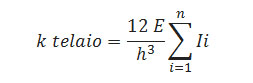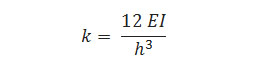
Il procedimento che segue descrive il calcolo relativo alla ripartizione delle forze orizzontali (sisma, vento…) sui telai che compongono la struttura rappresentata si seguito, attraverso il metodo delle rigidezze.

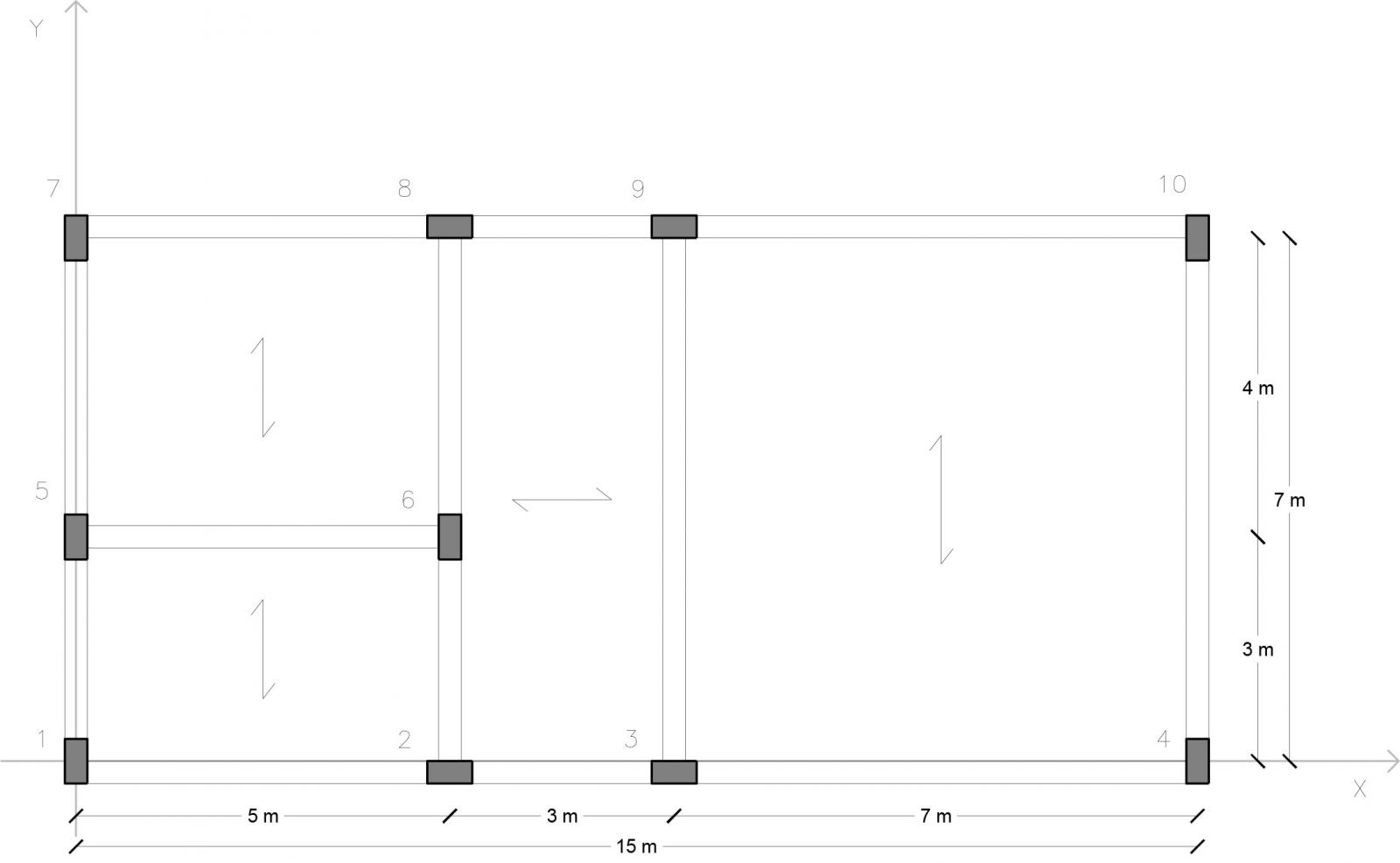
Si identificano nell’impalcato tutti i telai che fungono da controventi per le forze orizzontali che agiscono sulla struttura, quindi:

v1 - pilastri: 1-5-7

v2 - pilastri: 2-6-8

v3 - pilastri: 3-9

v4 - pilastri: 4-10

o1 - pilastri: 1-2-3-4

o2 - pilastri: 5-6

o3 - pilastri: 7-8-9-10

questi possono essere rappresentati come “molle”, e costituiscono i vincoli cedevoli elasticamente dell’impalcato:

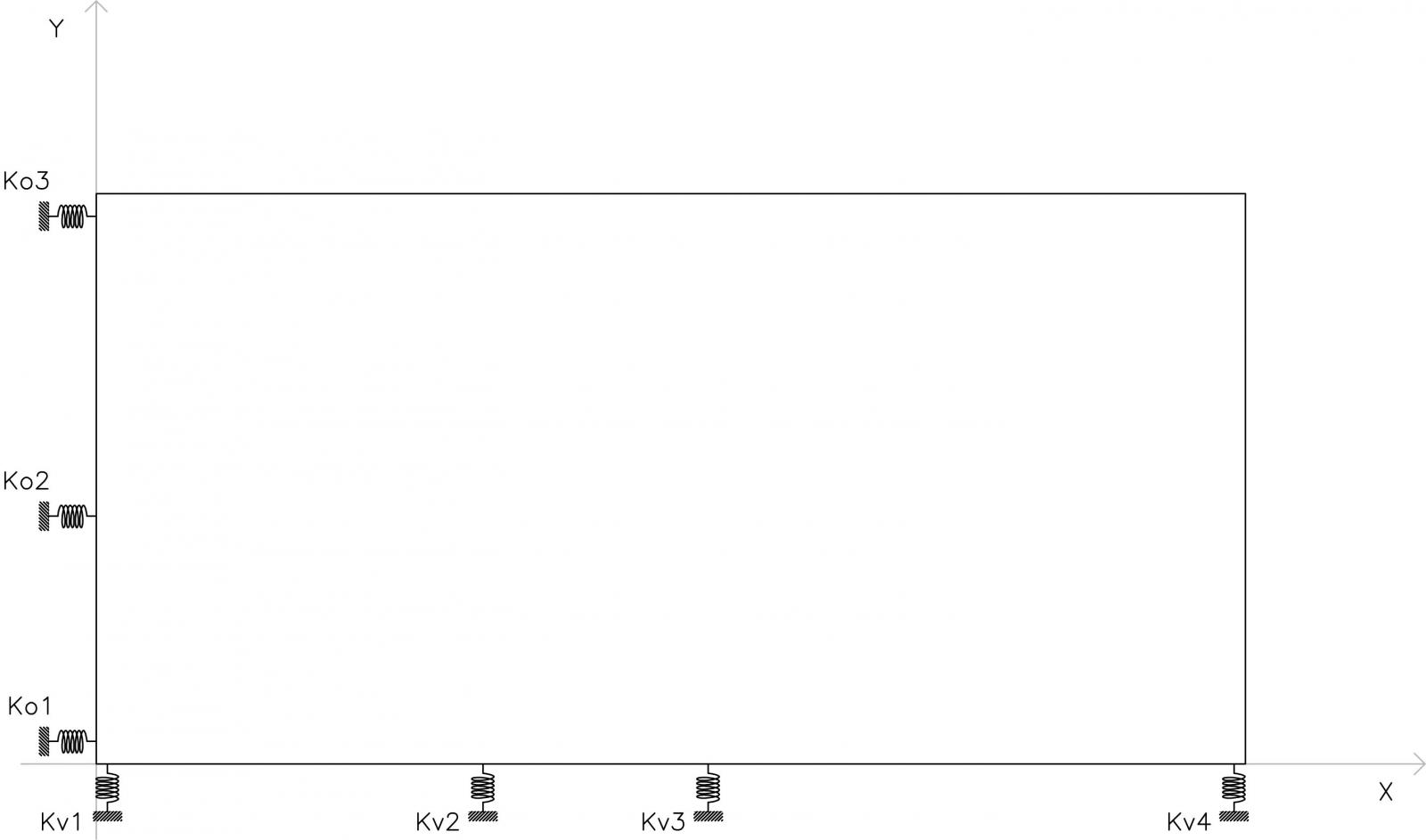
Ipotizzando che il solaio, rappresentato successivamente, sia rigido a sufficienza da considerare la struttura composta da telai Shear-Type, possiamo calcolare la rigidezza traslante K_T di ogni telaio, ovvero la somma delle rigidezze dei singoli pilastri che lo compongono, la quale come sappiamo dipende dal modulo di Young E, dal Momento d’Inerzia I e dalla luce L (nello specifico l’altezza h).

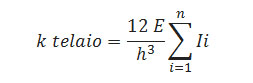
poiché il telaio Shear-Type ha una rigidezza pari a:

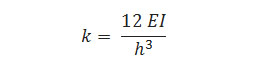
meglio sintetizzata nell’immagine qui sotto:

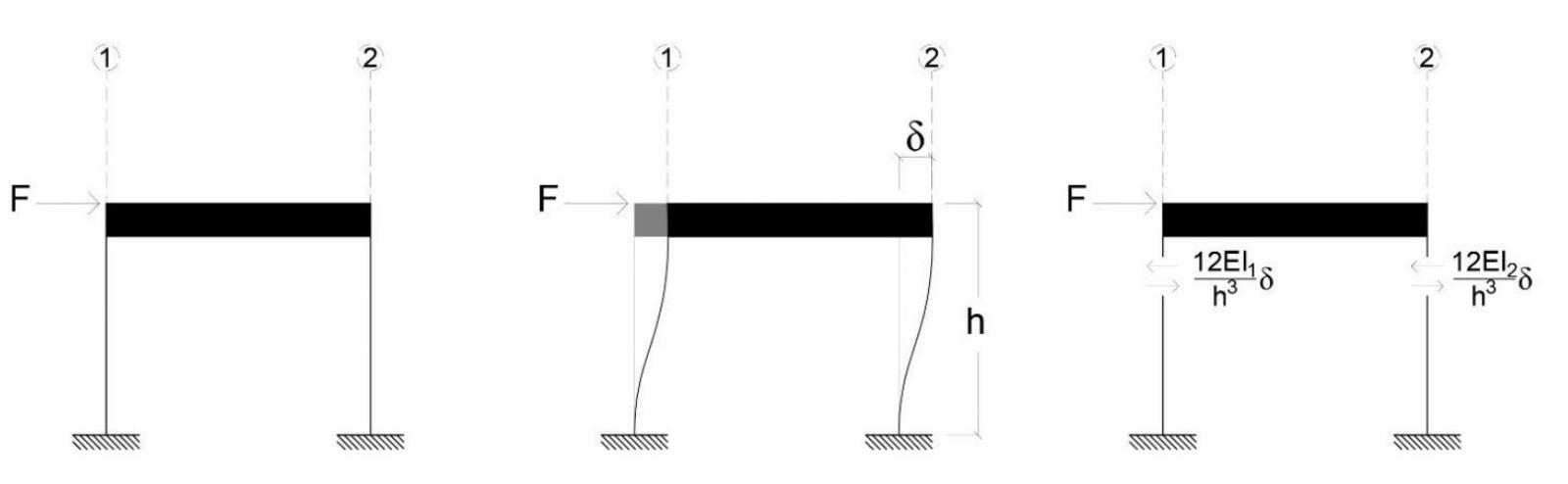
Step-1: Con la formula della rigidezza vista prima possiamo calcolarla per tutti i telai orizzontali e verticali identificati, definendo:

E = 21000 N/mm²

H = 4mt

Ix = bh³/12 *

Iy = b³h/12 *

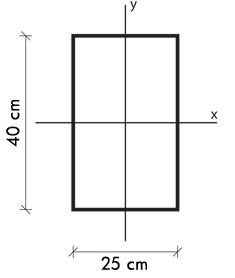
*rappresentazione della sezione rettangolare scelta per i pilastri dei telai Shear-Type

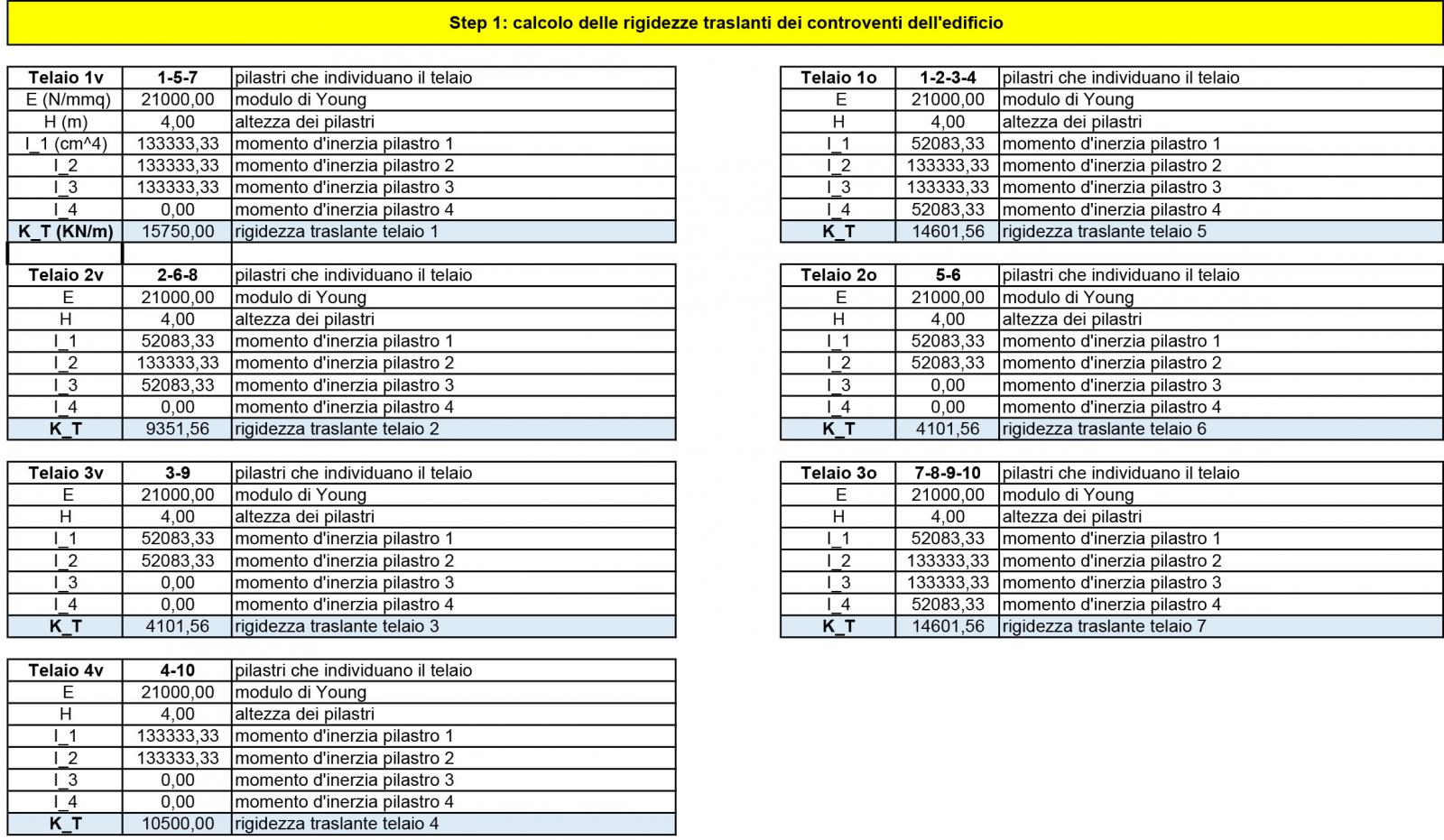
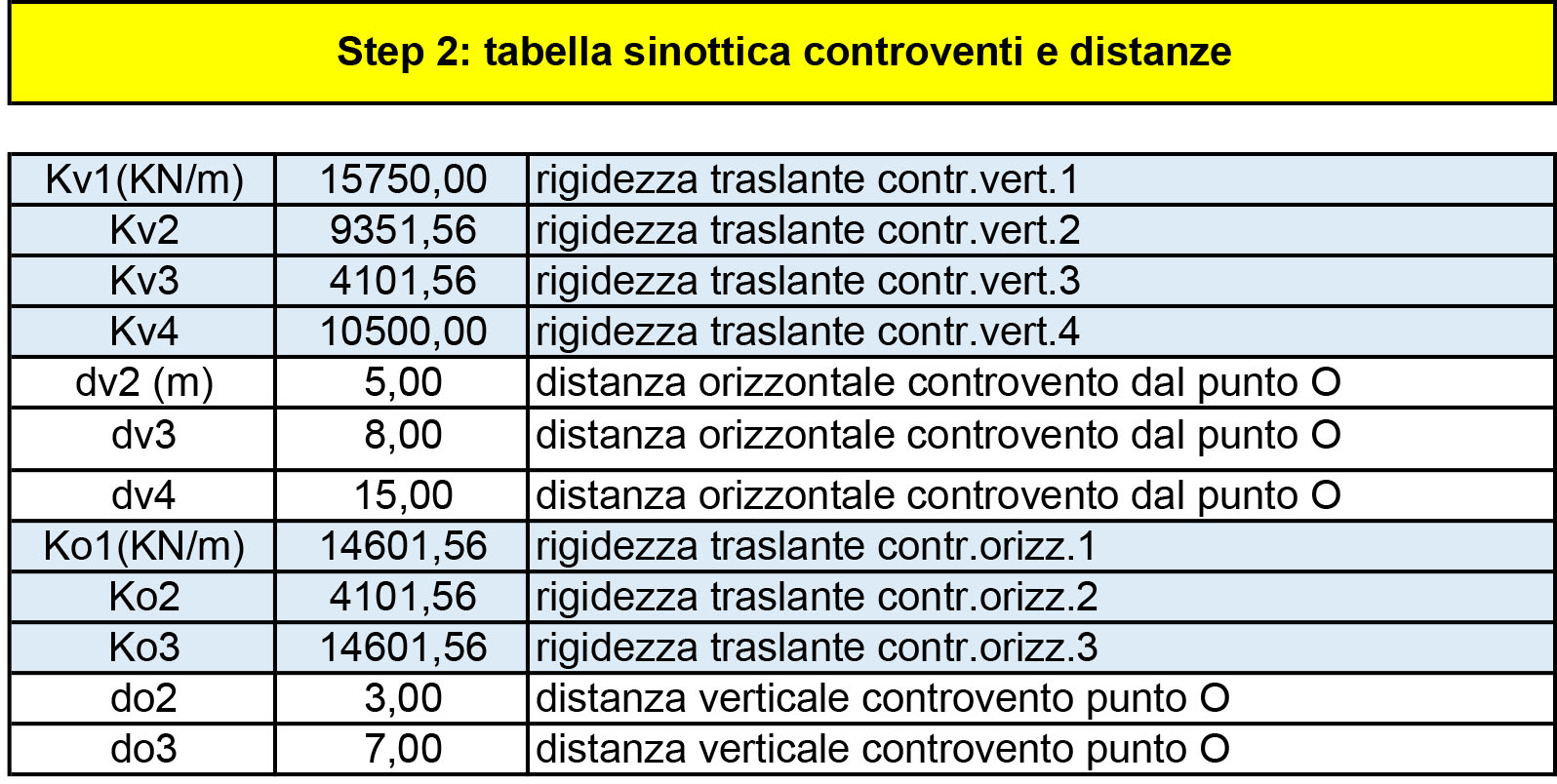
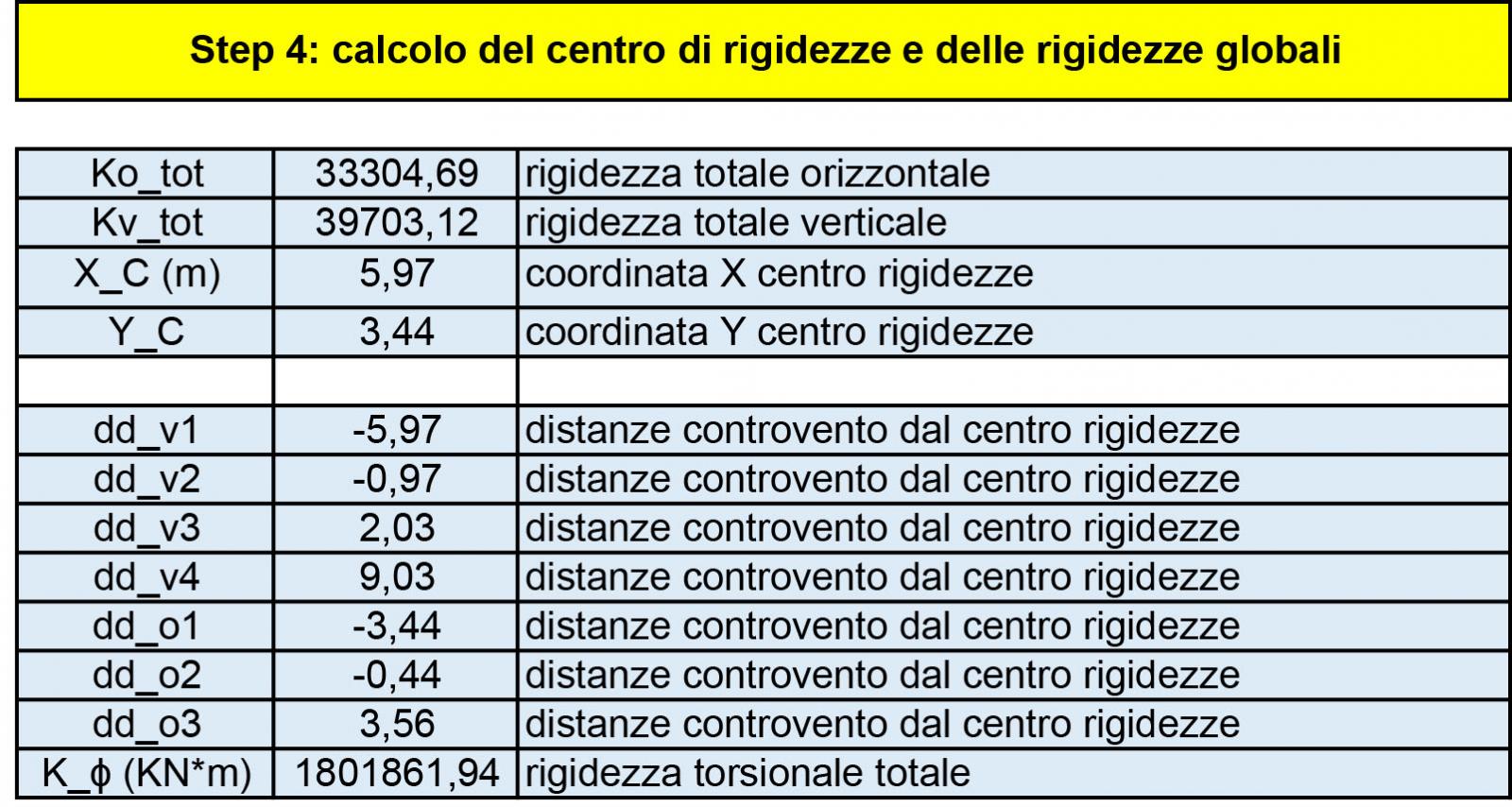
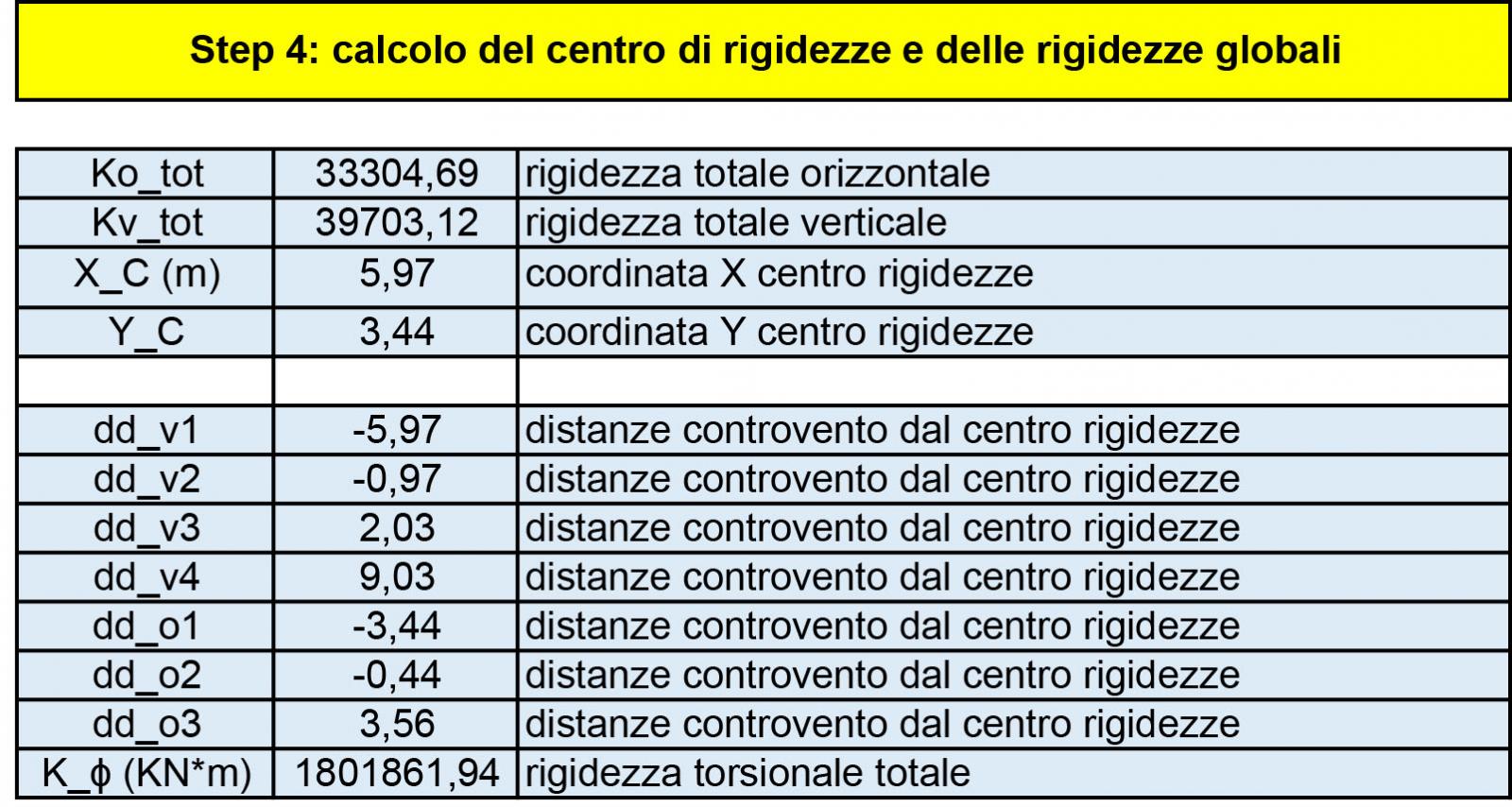
Step-2: Si riportano in tabella tutte le rigidezze calcolate nello step-1, con relative distanze tra esse e l’origine degli assi posto in basso a sinistra dell’impalcato:

La tabella riassuntiva riportata qui sopra servirà poi per velocizzare i calcoli del centro di rigidezza che viene calcolato nello step-3

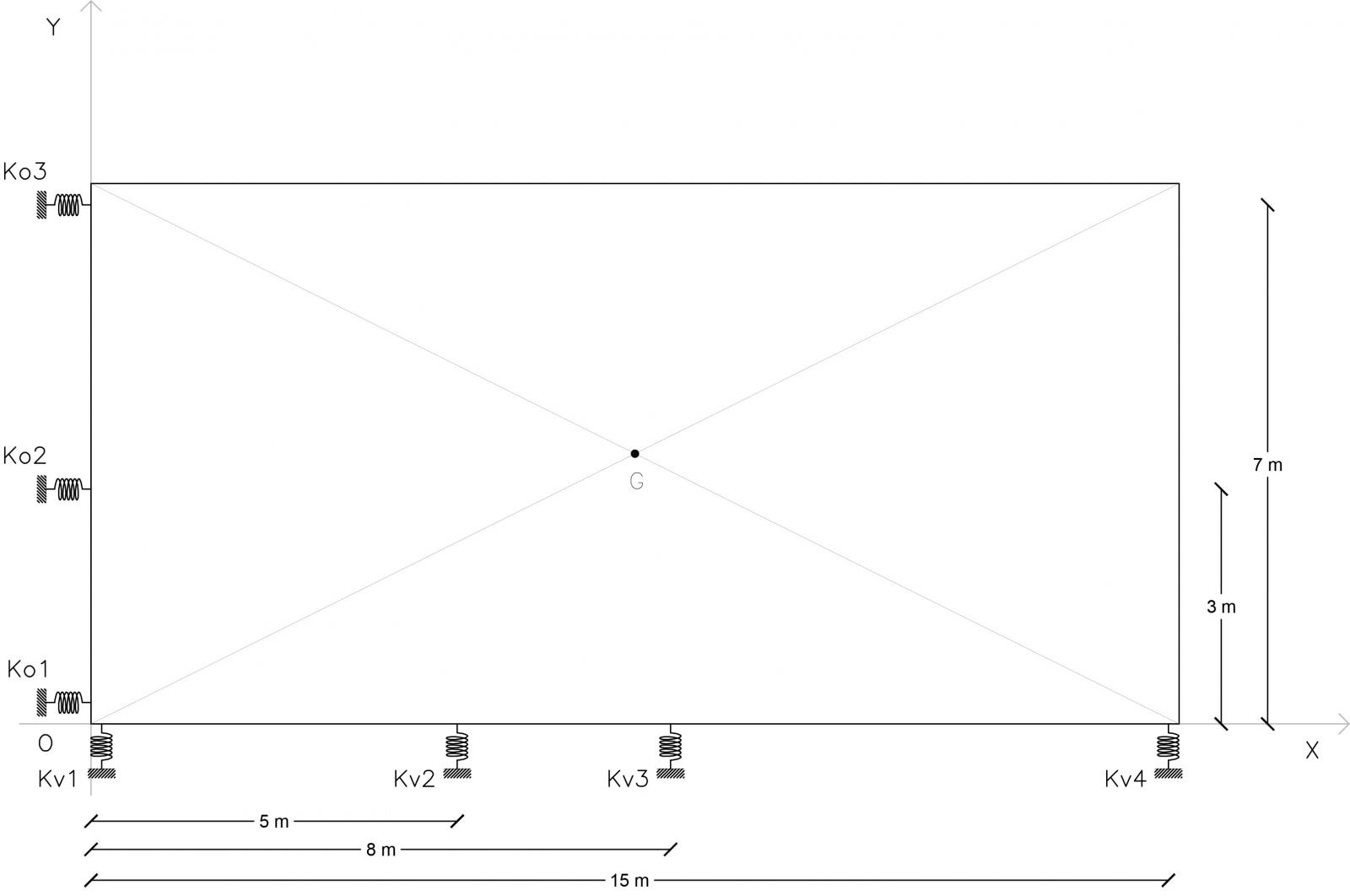
Step-3: Per capire dove applicare la forza orizzontale, che servirà per i calcoli successivi, si ricava il centro di massa dell’impalcato dal procedimento che segue:

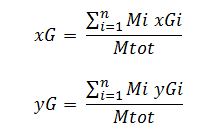
Così procedendo si ricavano le coordinate xG e yG che descrivono il centro di massa, ipotizzando che questo abbia la stessa densità per tutta la sua estensione, si ricava ponendo come la massa l’area della parte di impalcato in esame, poiché a parità di densità di tutto l’impalcato, il centro di massa coincide con il centro d’area.

Il procedimento è sintetizzato nella tabella sottostante che evidenzia un'unica area poiché essendo questo un impalcato “semplice” non vi è l’esigenza di dividerlo in parti:

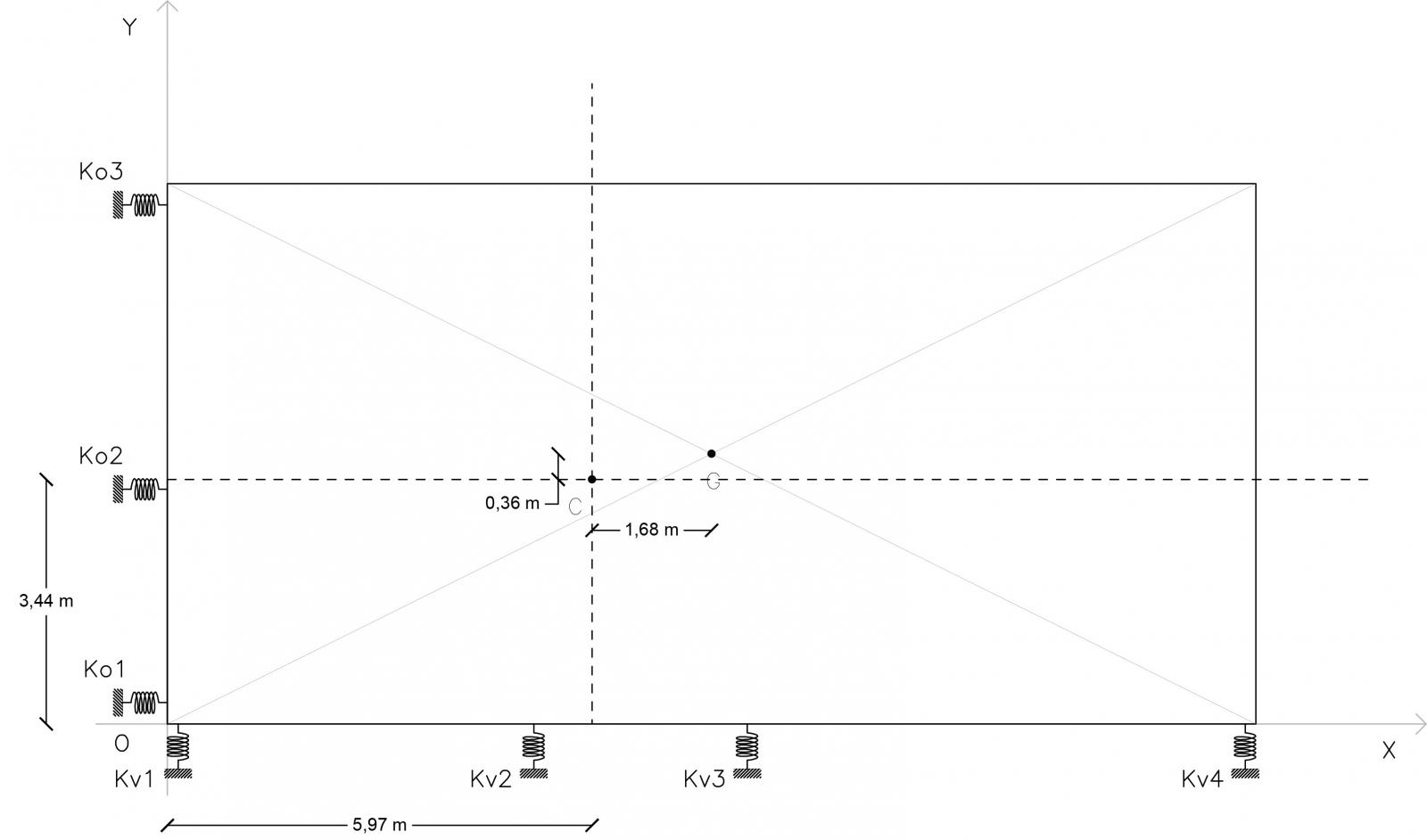
Nell’immagine qui sopra è riportato l’impalcato con i due punti del centro di massa e del centro di rigidezza con le quote della loro distanza.

Non coincidendo questi due punti, nel momento in cui si applica una forza orizzontale (nel centro di massa dell’impalcato) si produrrà uno spostamento sull’asse in cui è applicata la forza ed un momento che farà ruotare l’impalcato con perno nel centro delle rigidezze e braccio pari alla coordinata che informa sulla distanza di questa forza dal centro delle rigidezze.

Qualora questi due punti coincidessero allora non vi sarà alcun momento ma solo spostamento.

Step-5: Nella seconda parte della tabella esposta prima, che si riporta di seguito, viene calcolata “Kφ” la rigidezza torsionale che si ricava tramite la sommatoria di tutte le rigidezze ricavate nello step-1 per la loro distanza dal centro delle rigidezze, ricavato nello step-4.

Questa rigidezza torsionale “Kφ” verrà utilizzato in seguito per il calcolo della rotazione dell’impalcato secondo una direzione:

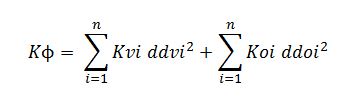
Step-5: Per analizzare la ripartizione delle forze orizzontali, manca ora solo il carico orizzontale, essendo questo ipotizzabile come una forza sismica, si ricava tale carico dalle operazioni che seguono:

Nella tabella qui sopra sono riportati i carichi qs, qp e qa che equivalgono ai valori del solaio in figura e dei carichi accidentali attribuiti a residenza:

Si ricavano i carichi G e Q, in accordo con le norme tecniche vigenti, dalle seguenti formule:

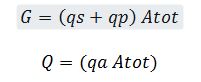
Si distinguono due carichi differenti per il calcolo dei carichi sismici W poiché il carico G presenta tutti i carichi “permanenti” legati ad elementi strutturali e non, mentre il carico Q racchiude tutti i carichi accidentali che vengono compresi nella combinazione sismica ridotti di un coefficiente di contemporaneità ψ.

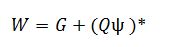
*Il valore di ψ è tabellato in normativa.

Questo carico W rappresenta la forza peso dell’edificio, espresso dalla massa dell’edificio per l’accelerazione di gravità.

Poiché il sisma ha un’accelerazione poco più piccola di quella di gravità, può essere introdotto un coefficiente riduttivo calcolato secondo la sismicità del luogo in cui si progetta la struttura:

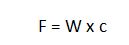
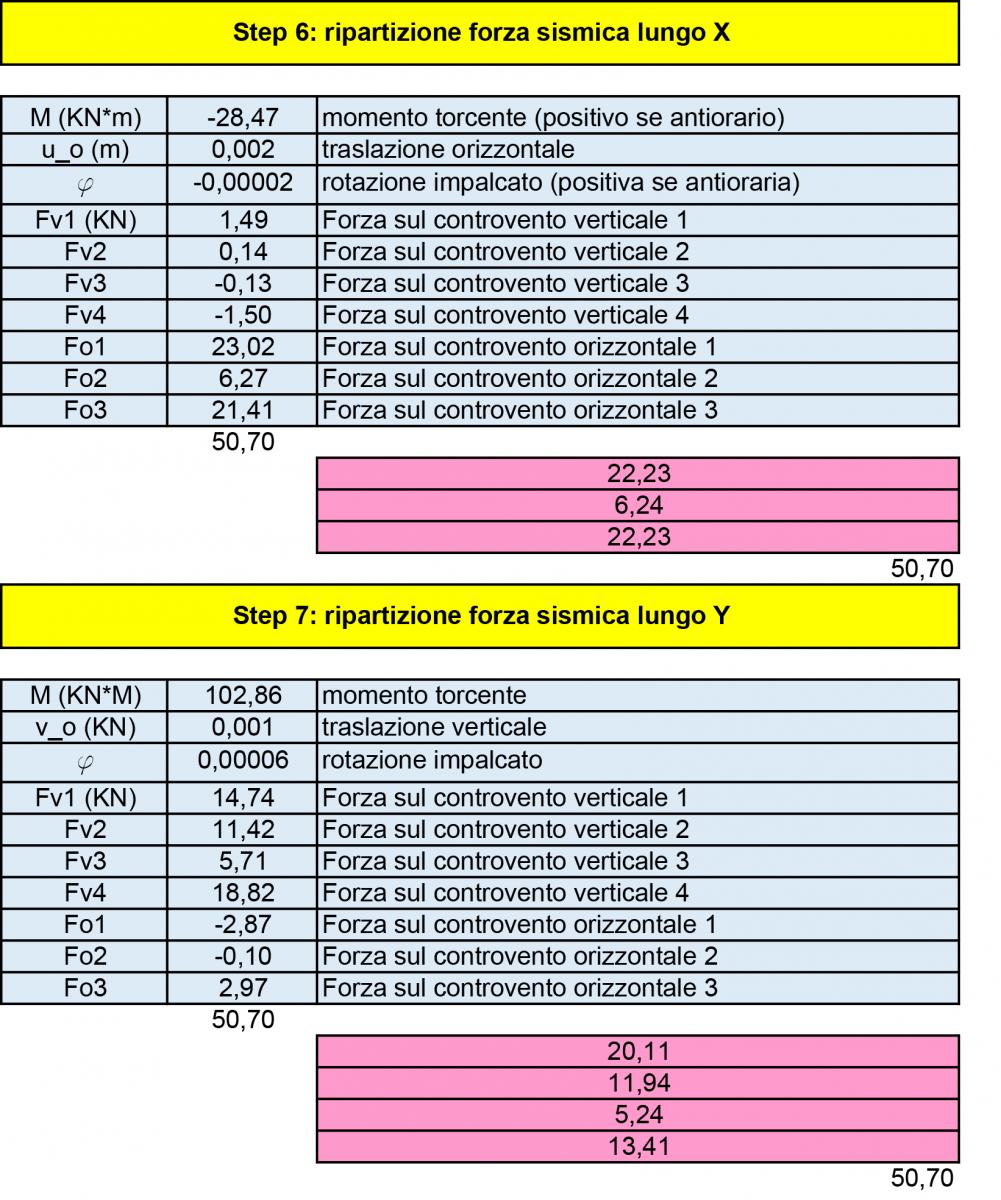
Step-6: Si dovrà ora quantificare la ripartizione della forza sismica F lungo l’asse x e lungo quello y e, nello specifico, per ognuno dei controventi. Si ricorda che nel momento in cui la forza agente abbia un asse differente da quello del centro delle rigidezze (come nel caso dell’impalcato in questione), il corpo non si limita a traslare, ma ha anche una rotazione. Per poter conoscere il valore di questa rotazione, si calcola il Momento Torcente M per l’asse x, moltiplicando la forza sismica F per il suo braccio, ovvero la differenza tra l’ordinata del centro delle rigidezze e quella del centro di massa, e per l’asse y, utilizzando come braccio la differenza tra le ascisse dei due centri. Poi, si calcola la traslazione orizzontale, dividendo F per la rigidezza traslante orizzontale, la traslazione verticale, dividendo F stavolta per la rigidezza traslante verticale, e le rotazioni, dividendo i rispettivi Momenti Torcenti per la rigidezza rotazionale “Kφ”: