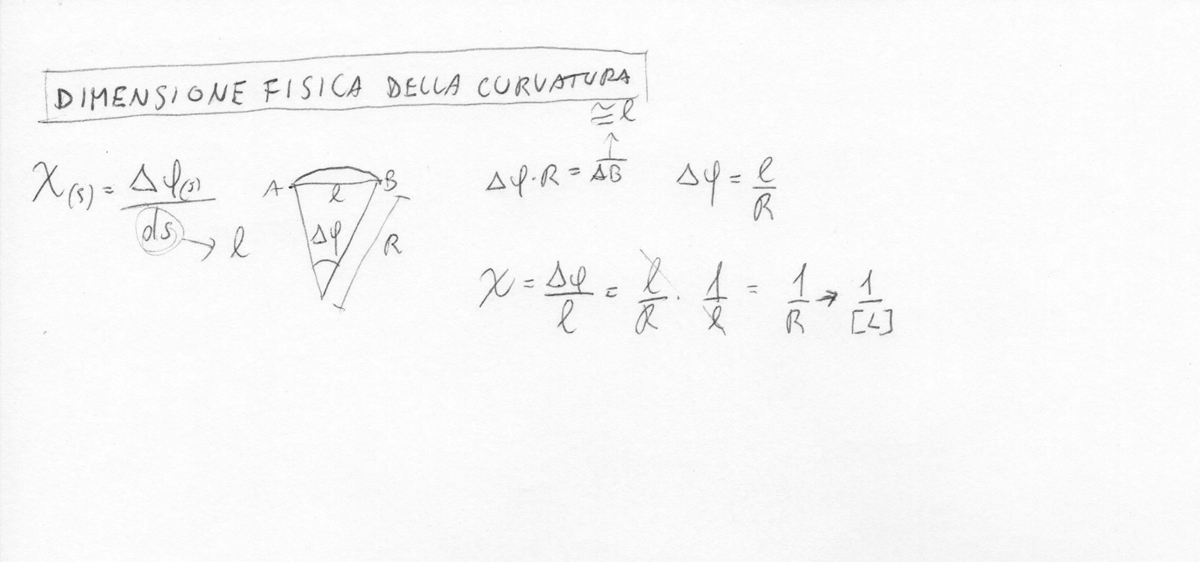
dimensione fisica della curvatura

considerando che la dimensione di v(s) e quindi uno spostamento sia (facendo le dovute semplificazioni dimensionali del termine per es. il primo (qs4/24EJ) sia [L]), di Phi(s) invece un numero adimensionale tale è l'ampiezza in radianti di un angolo è lecito pensare che continuando a togliere una dimensione al termine di Chi(s)=-qs2/2EJ, questa sia 1/[L] ovvero [L]-1; ed in effetti è così (fatte le dovute semplificazioni), ciò potrebbe esser dovuto al fatto che Chi in sostanza essendo la curvatura, ovvero un rapporto fisso tra angolo è lunghezza (ovvero l'arco di inflessione non per forza di circonferenza), ripresenta la dimensione lunghezza, la l'angolo è in radianti (quindi adimensionale) la lunghezza d'arco invece è dimensionalmente [L], che stando al denominatore è [L]-1

ecco algebricamente da dove viene la dimensione fisica, tramite una piccola dimostrazione