ESERCITAZIONE 4_ RIPARTIZIONE DELLE FORZE SISMICHE E CENTRO DI RIGIDEZZA

Con questa esercitazione analizziamo la ripartizione di una forza orizzontale (per esempio vento o sisma) su un edifico, possiamo così vedere la reazione di ogni telaio che compone l’impalcato e calcolare il centro di rigidezza.

L’impalcato analizzato è formato da telai piani in cls armato, di cui conosciamo la rigidezza poiché li considero come modelli Shear-type, un modello teorico che ipotizza l’uso di travi infinitamente rigide che non subiscono flessione, in modo da considerare solo il cedimento vincolare δ di ogni pilastro e quindi la rigidezza di questi.

Conosciamo la rigidezza di ogni controvento modello Shear-type che è:

F=kδ

k=12EI₁/hᶟ + 12EI₂/hᶟ

Generalizzando la formula da 2 a n pilastri

k=12EI/hᶟ ∑ᶰᵢ‗₁ Iᵢ

F= (12EI₁/hᶟ + 12EI₂/hᶟ) δ

Dall’analisi dell’impalcato possiamo individuare 8 telai piani (5 verticali e 3 orizzontali).

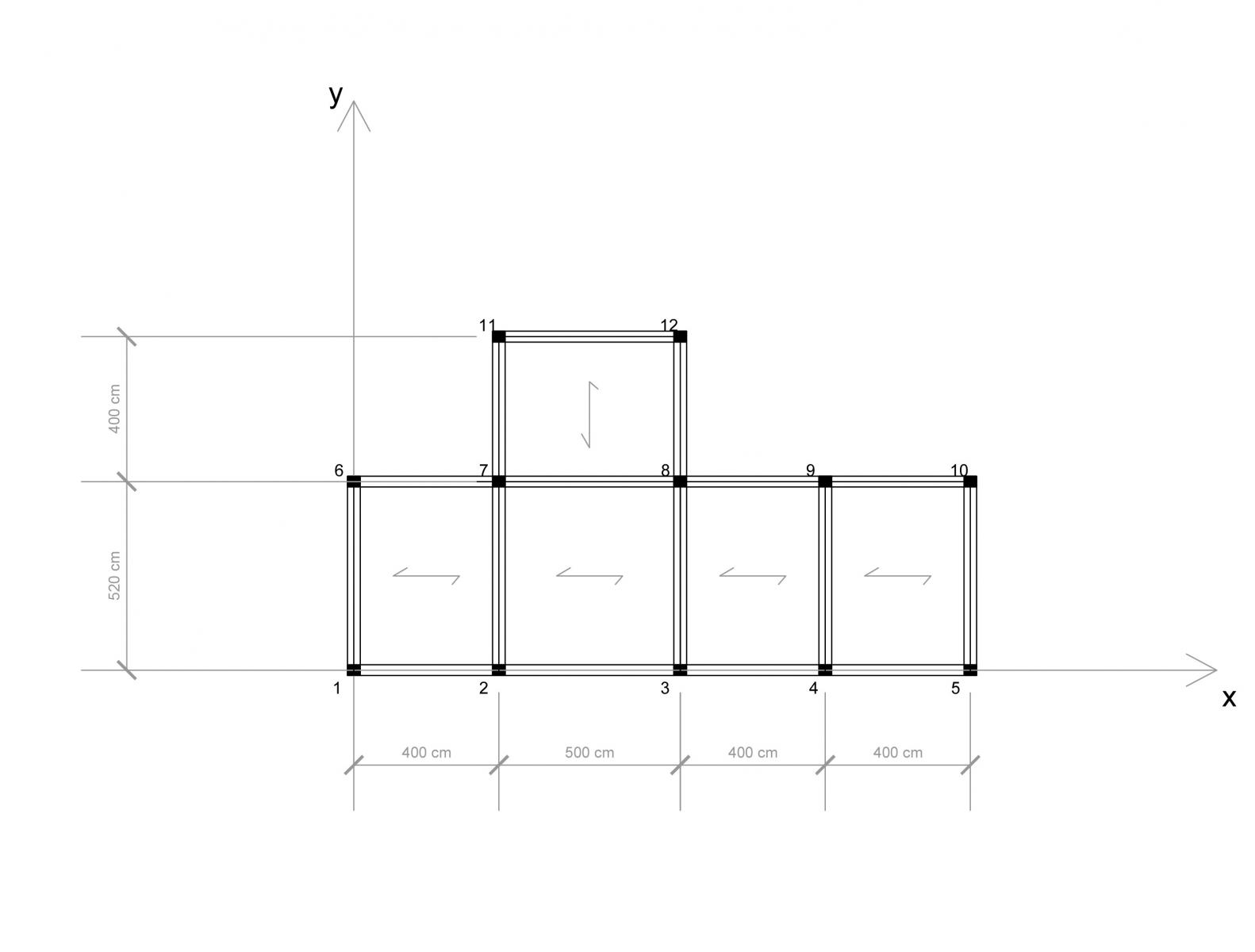
Telai verticali

Telaio 1v               1-6

Telaio 2v               2-7-11

Telaio 3v               3-8-12

Telaio 4v               4-9

Telaio 5v               5-10

Telai orizzontali

Telaio 1o               1-2-3-4-5

Telaio 2o               6-7-8-9-10

Telaio 3o               11-12

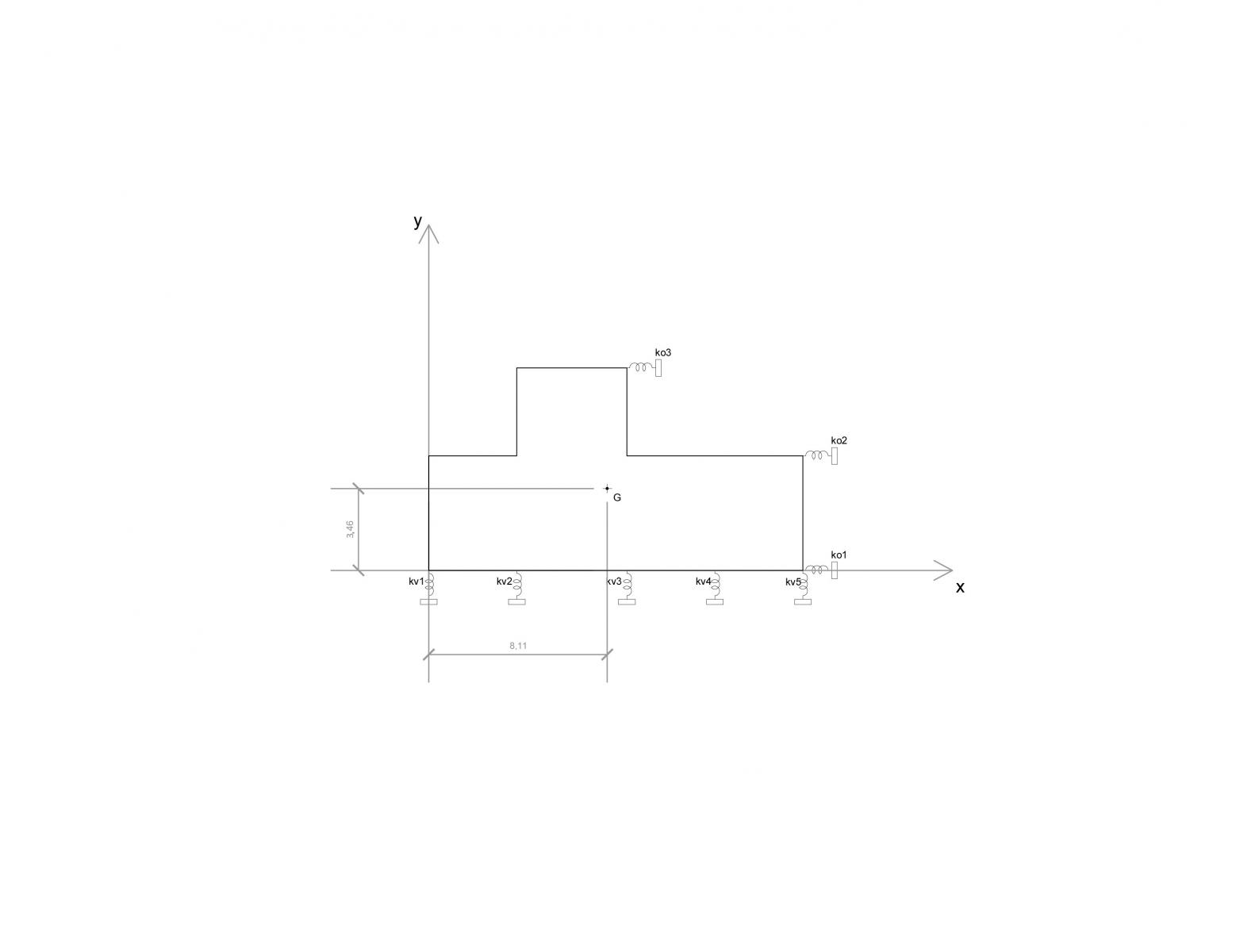
Ipotizzo i telai/controventi come vincoli cedevoli elasticamente e rappresentabili nel piano dell’impalcato xy (i telai vivono nei piani xz e yz) come molle di adeguata rigidezza k.

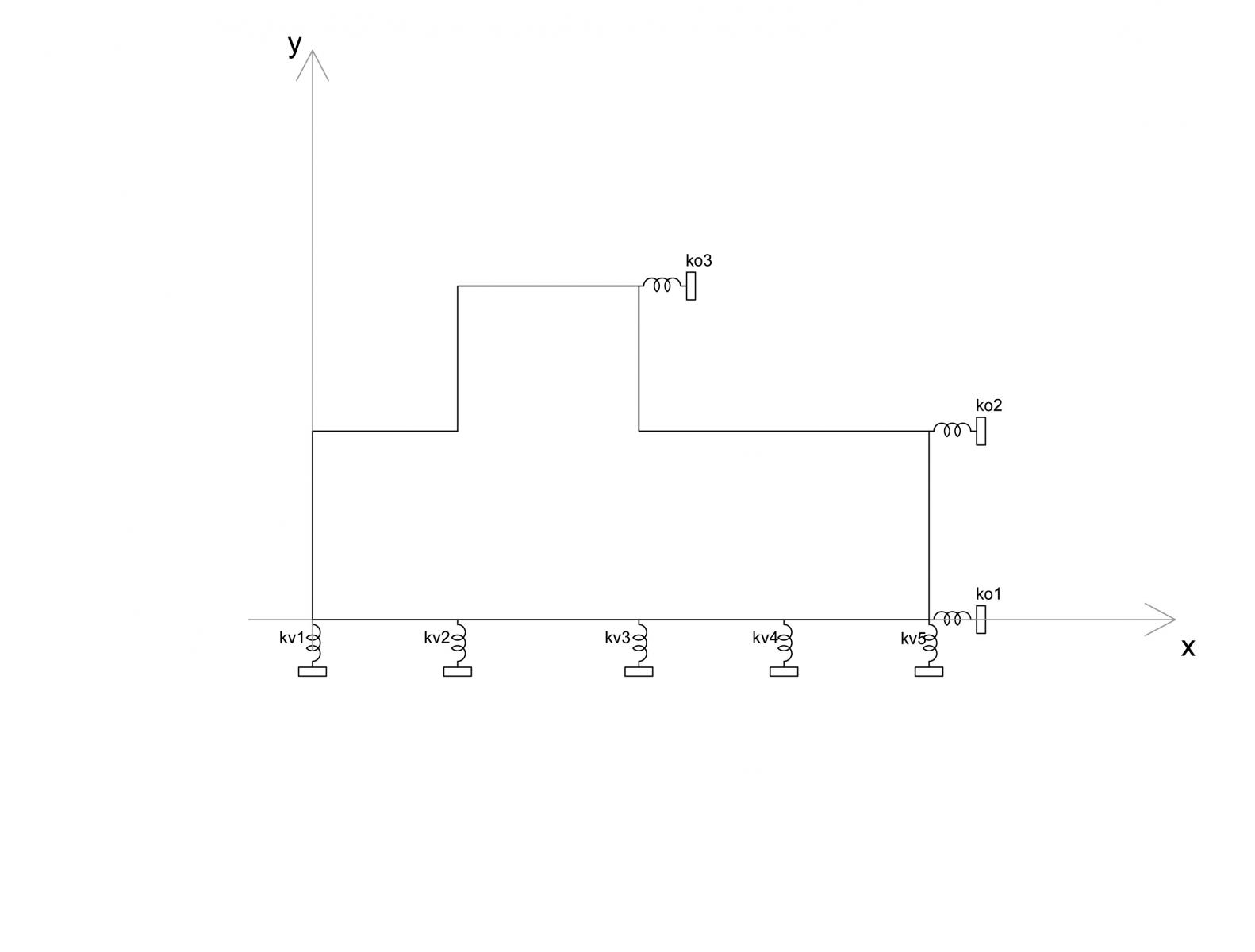
-Ora grazie ad un foglio Excel posso calcolare la rigidezza di ogni singolo controvento, tenendo presente che:

I pilastri sono a sezione rettangolare e misurano 40x40 cm quindi Ix=Iy

I = 40cm x 40 cm³/12 = 213333,33 cm⁴

-Trovate le rigidezze traslanti k calcoliamo le loro distanze dal punto d’origine O.

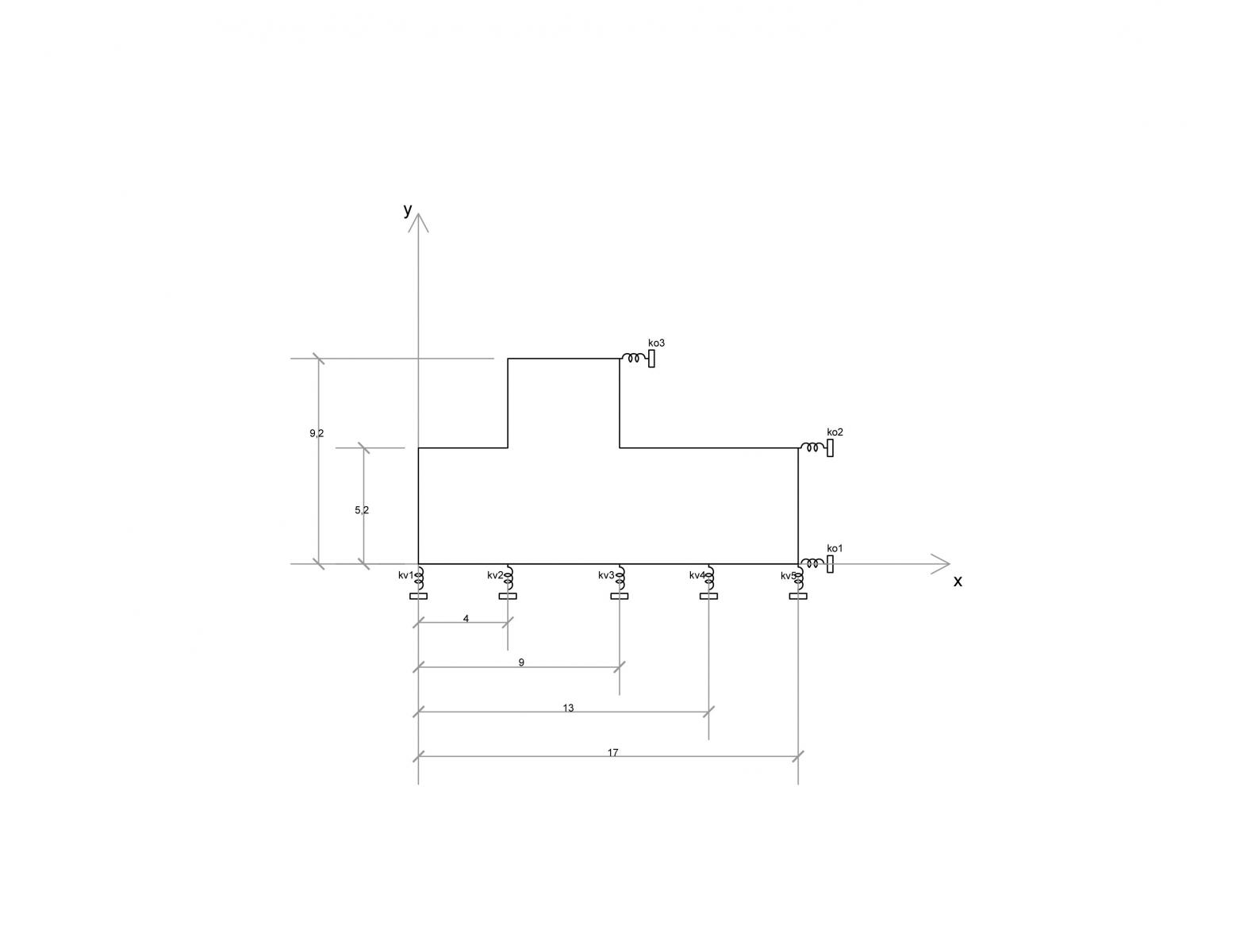
-Ora è possibile trovar il centro d’area dell’edificio: G. poiché si tratta di una geometria “complessa”, scompongo la pianta in due rettangoli di cui conosco i rispettivi centri d’area.

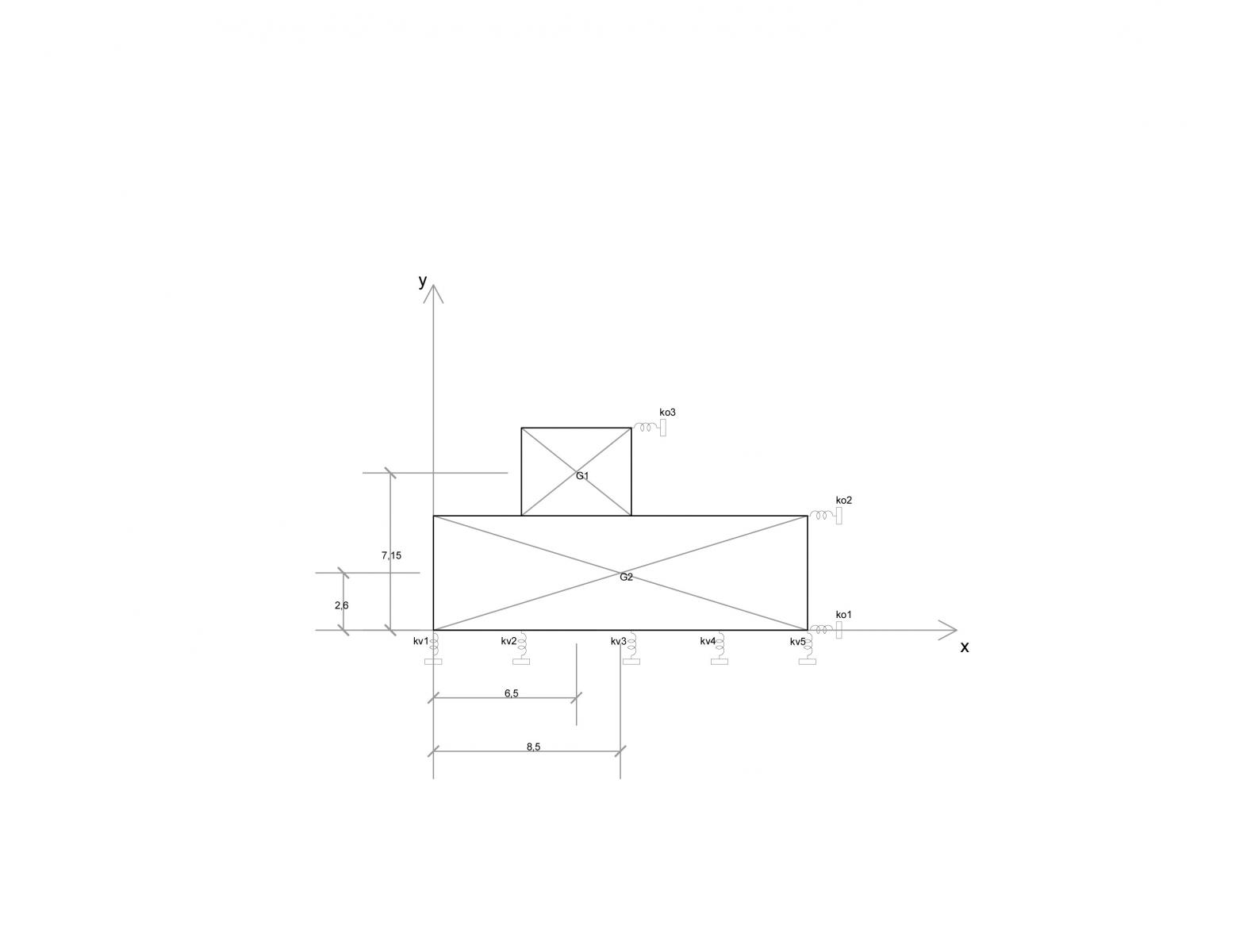
G1:                             x1 = 7 ,15m

                                   y1 = 6,5m

G2:                             x2 = 2,6m

                                   Y2 = 8,5m

Per trovare G sappiamo che

                                   xG = (A1 xG1 + A2 xG2 )/Atot     

                                   xG = (20mq  7,15m + 85mq 2,6 )/105mq = 3,45 m                          

                                   yG = (A1 yG1 + A2 yG2 )/Atot     

                                   yG = (20mq  6, 5m + 85mq 8,5m )/105mq = 8,13m          

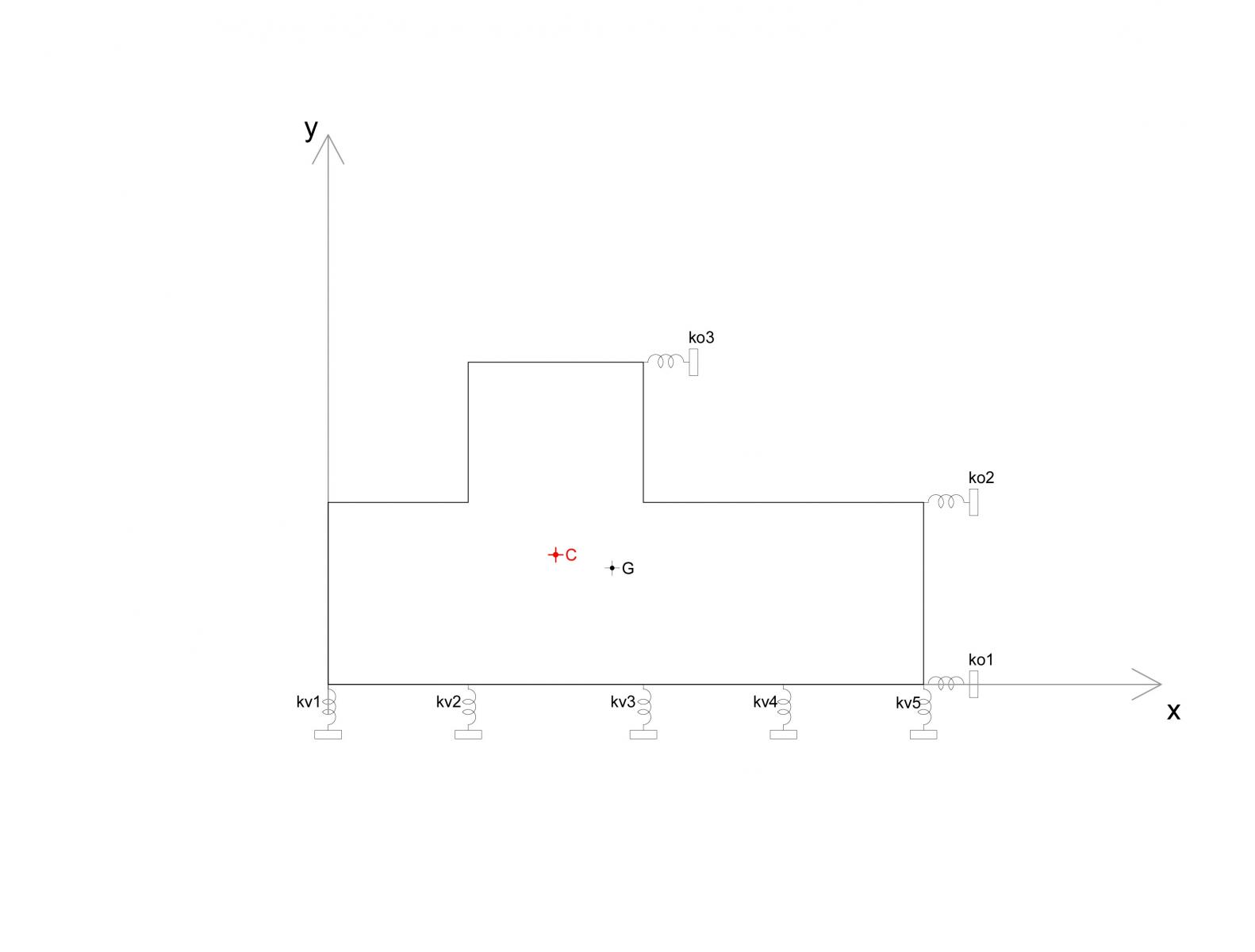
-Tramite Excel calcoliamo la rigidezza totale orizzontale (somma delle rigidezze di ogni controvento orizzontale), e allo stesso modo le calcoliamo le rigidezze verticali e la rigidezze torsionale globale e il centro delle rigidezze C. Dove:

xC=∑kvᵢ dvᵢ/kvtot

xC=∑koᵢ doᵢ/kotot

kφ=∑kvᵢ dd2vᵢ + ∑koᵢ dd2oᵢ

In questo modo posso vedere quanta è la distanza tra G e C. I due punti devono essere il più vicino possibile; infatti la forza orizzontale agisce direttamente sul centro delle rigidezze C e è necessario diminuire il più possibile il la distanza tra G e C che è il braccio per cui si moltiplica la forza che provoca la rotazione del corpo intorno a G.

Naturalmente per avvicinare i due punti tra loro devo agire sulle singole rigidezze dei telai e quindi sui momenti di inerzia dei pilastri. 

-Da normative è possibile fare un’analisi approssimativa per valutare la forza sismica (Fs).

                       Fs =W c

Dove W rappresenta la forza peso dell’edificio, data dal prodotto tra la massa e l’accelerazione di gravità permanente g. per definire il peso è necessario conoscere i carichi agenti sull’edificio.

Quindi definiti i carichi q_s, q_p e q_a agenti sull'impalcato, trovo il carico totale permanente G tramite la formula:

                                                      G = (q_s +  q_p  ) A_tot

ed il carico totale accidentale Q tramite la formula:

                                                      Q = qa x A_tot

Ora è possibile calcolare il peso sismico W:

                                          W = G + Ψ_2j x Q 

Ψ_2j = coefficiente di contemporaneità.

 -Poiché è impossibile sapere in che direzione si applicherà la forza orizzontale ipotizzo che essa agisca nei due casi peggiori, quindi lungo l’asse x (dove reagiscono solo i telai verticali) e lungo l’asse y (dove reagiscono solo gli orizzontali).

La Fs applicata lungo l’asse x comporterà quindi una possibile rotazione e traslazione orizzontale.

La Fs applicata lungo l’asse y comporterà quindi una possibile rotazione e traslazione verticale.

Dove :

lo spostamento orizzontale         u= F/ko_tot

Lo spostamento verticale             v= F/kv_tot

La rotazione                                     φ=M/k φ

E M è il momento torcente dato da Fs per il braccio (distanza C e G).

Determinati i valori dei gradi di libertà è possibile ricavare la forza sui singoli controventi nei due casi di carico.