Es_3 Dimensionamento e verifica di una trave a sbalzo

La seguente esercitazione mostra il dimensionamento di una trave a sbalzo di un generico solaio in c.a., in acciaio e in legno.

L'impalcato di riferimento è il seguente:

Troviamo l’area d’influenza maggiore tra le tre travi a sbalzo, esattamente come abbiamo fatto per l’esercitazione precedente, considerando però che non si tratta più di una trave doppiamente appoggiata, ma di una mensola quindi il M_max = Ql²/2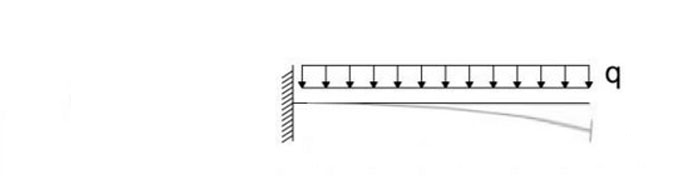 

Una volta dimensionata la sezione della mensola sarà necessario verificare la sua deformabilità controllando che l’abbassamento massimo dell’elemento non sia maggiore di 1/250 della luce. Questo procedimento si effettua allo Stato Limite di Esercizio in quanto ci interessano spostamenti e deformazioni della trave, azioni che possono compromettere l’uso e la funzione dell’edificio. Attraverso il foglio Excel calcoliamo la combinazione frequente allo SLE. 

 l/ v_max > 250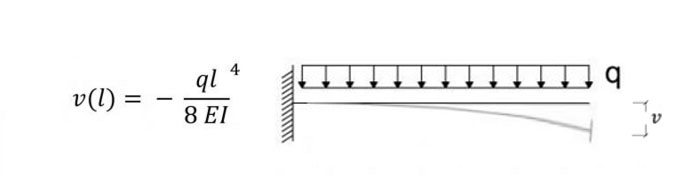   

Solaio incalcestruzzo armato

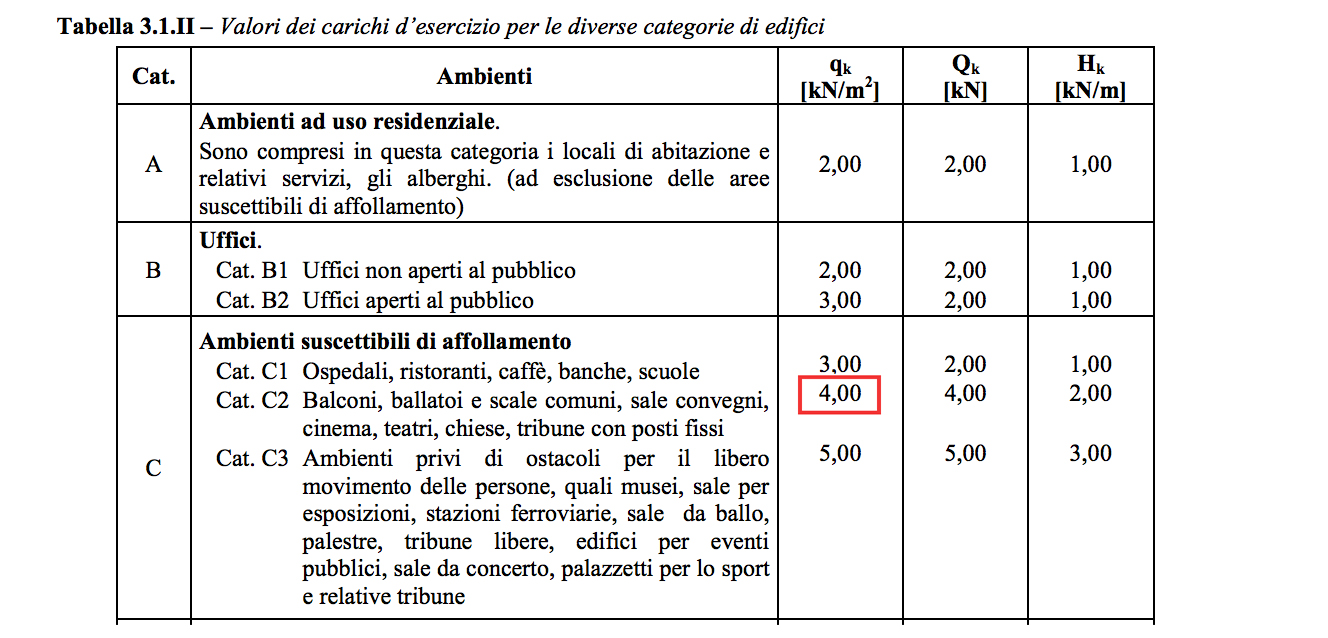
Il solaio analizzato è in latero cemento armato, con categoria di destinazione d’uso C2, cioè ambienti suscettibili di affollamento come i balconi o ballatoi.  

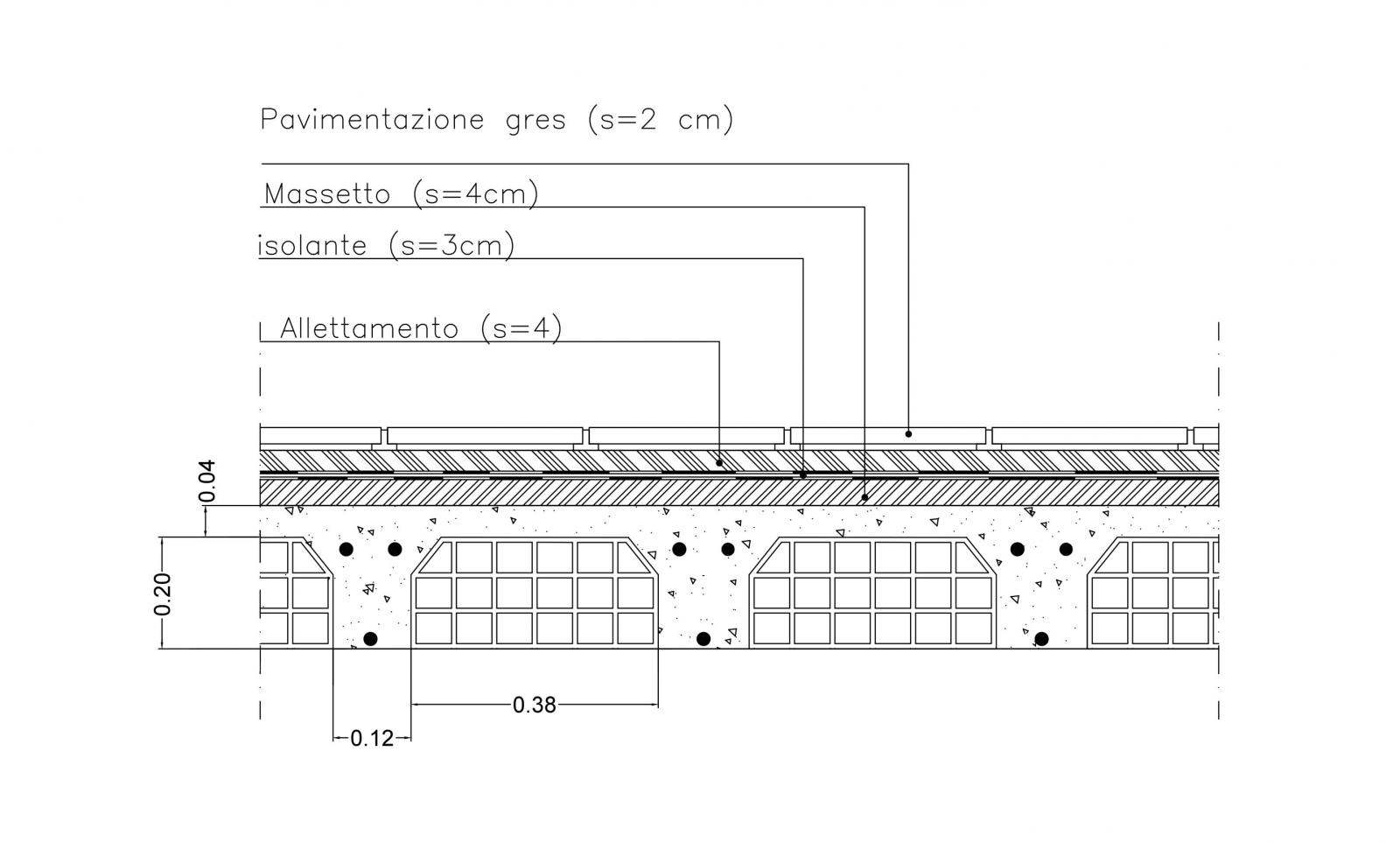
Peso proprio della struttura

q_s = 3,12 KN/m²

Peso portato dalla struttura:

q_p = 3,95 KN/m²

Carico accidentale:

q_a  = 4,00 KN/m²

Calcoliamo il carico totale attraverso una tabella Excel

KN/ m² (3,12 + 3,95 + (4,00 · 1,5)) 5,5 m =54,29 KN/m = q_u

Calcoliamo il momento massimo

M_max =  434,28 KNm

Una volta trovato il valore del momento massimo procediamo scegliendo il tipo di acciaio (nel nostro caso acciaio S450) e di calcestruzzo (C30) determinando i valori delle tensioni caratteristiche di progetto del calcestruzzo f_cd e quella delle barre d’acciaio f_yd attraverso i valori della resistenza dei due materiali:

 f_cd = α_cc f_ck/g_c

f_yd = f_yk/g_m

Definendo ora la base della sezione e noti i valori delle tensioni di progetto calcoliamo l’altezza utile da sommare al copri ferro per ottenere l'altezza minima della sezione anche attraverso b e r.

Andiamo ora a verificare le dimensioni appena definite della sezione (40x60) aggiungendo il peso proprio della trave e ricontrollando l’abbassamento. 

Solaio in Legno

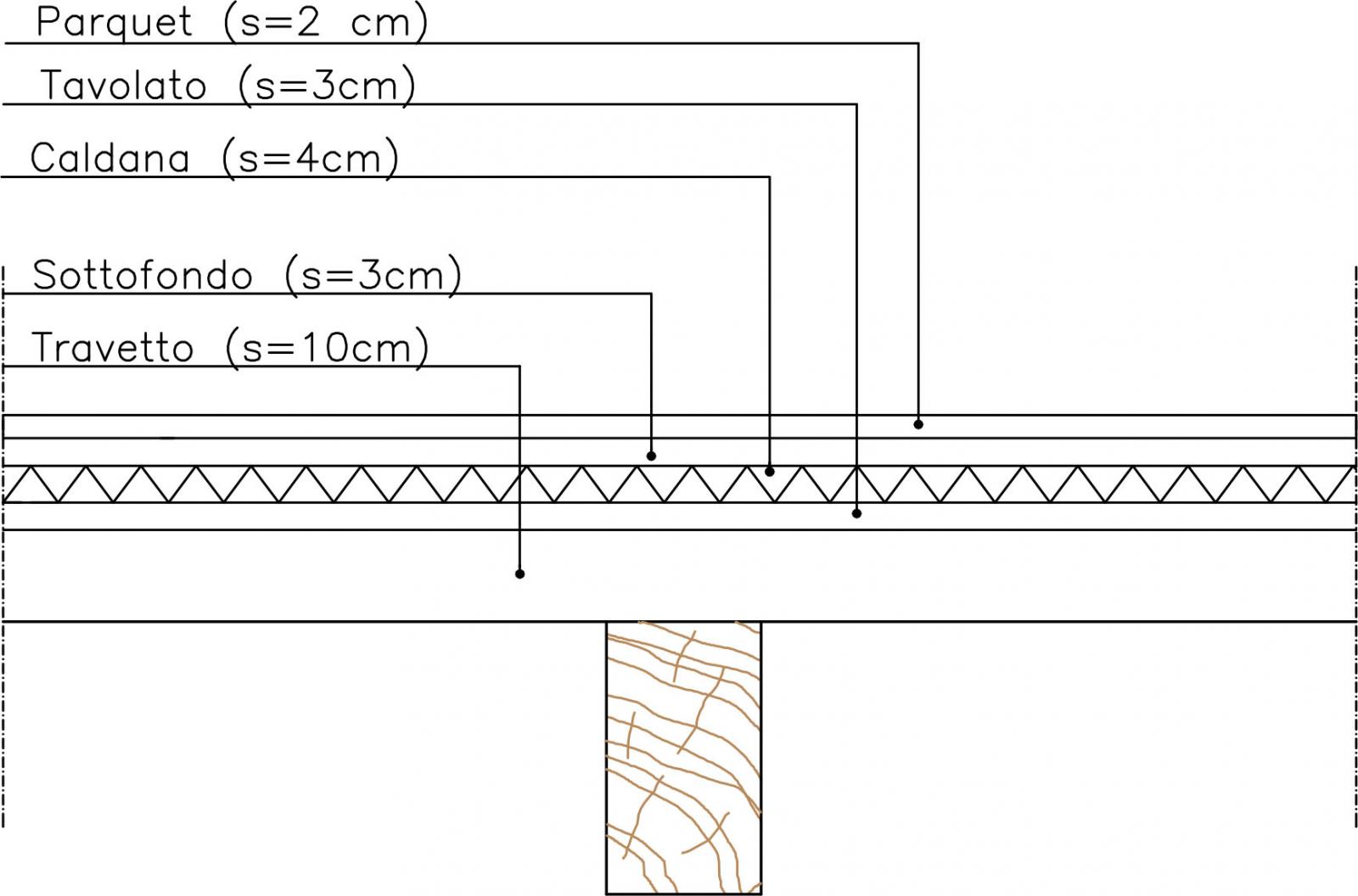
Peso proprio della struttura

q_s = 0,27 KN/m²

Peso portato dalla struttura:

q_p = 2,74KN/m²

Carico accidentale:

q_a  = 4,00 KN/m²

E procediamo inserendo il valore caratteristico a flessione del legno che scegliamo in base alla classe di resistenza f_mk, il coefficiente parziale di sicurezza g_M, e il coefficiente diminutivo del valore di resistenza. Attraverso questi valori calcoliamo la tensione di progetto f_d.                

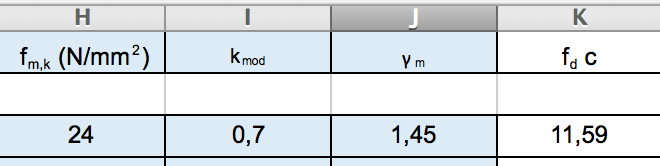
Stabiliamo ora la misura della base, e troviamo attraverso la formula 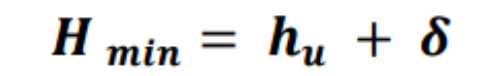l’altezza minima che dovrà avere la nostra sezione.

Una volta trovata l’altezza minima la sezione ingegnerizzata risulta essere di 60x65 cm.

In questo caso il peso proprio della trave in legno non viene considerato in quanto è un materiale leggero.

Solaio in Acciaio

Peso proprio della struttura

q_s = 2,55 KN/m²

Peso portato dalla struttura:

q_p = 3,45 KN/m²

Carico accidentale:

q_a  = 4,00 KN/m²

In base hai carichi calcolati, troviamo il momento massimo e scegliamo il tipo di acciaio: S355. 

Calcoliamo ora il modulo di resistenza a flessione -W_x- che deve essere minore di quello di progetto -W_d- e andiamo a scegliere il profilo della nostra IPE sul sagomario.

Il profilo adottato è un’IPE 500.

Verifichiamo ora che il rapporto tra la luce della trave e l’abbassamento massimo non sia superiore a 250, come prevede la normativa. 

Per calcolare l’abbassamento quindi aggiungo al -q_u- il peso proprio della trave data dal sagomario, calcolato nella combinazione allo SLE -q_e-, definisco il modulo elastico del materiale -E- e il momento d’inerzia -I-.

Il profilo risulta essere verificato.