blog di matilde.panascì

Questa esercitazione è finalizzata a calcolare come viene ripartita una forza orizzontale, come può essere il vento o il sisma, su un generico impalcato strutturale ad un piano. Calcoleremo quindi le rigidezze dei controventi, il centro d’area e il centro delle rigidezze dell’impalcato trovando così gli spostamenti prodotti dalla forza.

L’impalcato preso in considerazione è costituito da telai piani in cemento armato con controventi di tipo Shear-type, la cui caratteristica è di avere travi infinitamente rigide questo fa sì che ai pilastri non vengano trasmesse rotazioni.

Per prima cosa poniamo l’impalcato in un sistema di riferimento cartesiano dove andiamo ad individuare i telai paralleli all’asse y e quindi verticali e i telai paralleli all’asse x quindi orizzontali:

 

Telaio 1v  composto da: pilastri  1, 7 e 11

Telaio 2v  composto da: pilastri  2, 4 e 8

Telaio 3v  composto da: pilastri  9 e 12

Telaio 4v  composto da: pilastri  3 e 5

Telaio 5v  composto da: pilastri  6 e 10

 

 Telaio 1o composto da: pilastri  1, 2 e 3

 Telaio 2o composto da: pilastri  4, 5 e 6

 Telaio 3o composto da: pilastri  7, 8, 9 e 10

 Telaio 4o composto da: pilastri  11 e 12

 

I controventi, che per il solaio rappresentano vincoli cedevoli elasticamente, possono essere schematizzati nel piano dell'impalcato come molle, aventi un’adeguata rigidezza.

Trattandosi di telai shar-type la loro rigidezza sarà data da:

 

Quindi in generale per un telaio di n pilastri la rigidezza sarà: 

Dove E rappresenta il modulo elastico del cls armato mentre I è il momento d’inerzia del pilastro secondo la direzione in cui resiste meglio. 

quindi per il pilastro da noi adottato avremo: 

Iy=(30*40^3)/12=160000

Ix=(40*30^3)/12=9000

       

Andiamo ora a calcolare la rigidezza traslante associata ad ogni controvento sapendo che l’altezza di ogni nostro pilastro è di 3,5 m e il modulo elastico del nostro materiale  è di 21000 N/mm^2.

Una volta definita la rigidezza di ogni controvento le riportiamo in tabella insieme alla sua distanza dall’origine. 

Ora vediamo come calcolare il centro di massa dell’impalcato (G).

Innanzi tutto dividiamo l’impalcato in forme geometriche elementari come i rettangoli, nel nostro caso tre, di cui definiamo l’area e il baricentro:

Area A: 11,70 m²

Area B: 6,43 m²

Area C:  8,43 m²

 

Centro A: (1,5 ;  3,9)

Centro B: (4,6 ;  2,9)

Centro C: (2,5 ;  0,97)

 

 

 

 

 

 

Applichiamo ora attraverso il foglio Excel la formula della sommatoria per trovare il centro di massa che risulta avere coordinate G (2,58 ; 2,73).

Definiamo ora le coordinate del centro delle rigidezze (Xc, Yc) attraverso la sommatoria che moltiplica le rigidezze traslanti  (kv, ko) per la distanza del controvento dall’origine (dv, do). 

Ricaviamo ora il valore delle rigidezza torsionale calcolando tutte le distanze dei diversi controventi (ddv, ddo) dal centro delle rigidezze (C) data dalla formula:

Nella tabella successiva possiamo calcolare il valore della forza sismica agente  sull’impalcato attraverso l’analisi dei carichi sismici.

Per far ciò riprendiamo i valori dei carichi strutturali, permanenti, e accidentali dell’esercitazione sul dimensionamento della trave:

q_s = 3,12 KN/m²

q_p = 3,95 KN/m²

q_p  = 2,00 KN/m²

Attraverso il foglio Excel e il valore dei carichi per unità di superficie (KN/mq) calcoliamo il carico totale permanete (G), il carico totale accidentale (Q) come segue:

La seguente esercitazione mostra il dimensionamento di una trave a sbalzo di un generico solaio in c.a., in acciaio e in legno.

L'impalcato di riferimento è il seguente:

Troviamo l’area d’influenza maggiore tra le tre travi a sbalzo, esattamente come abbiamo fatto per l’esercitazione precedente, considerando però che non si tratta più di una trave doppiamente appoggiata, ma di una mensola quindi il M_max = Ql²/2 

Una volta dimensionata la sezione della mensola sarà necessario verificare la sua deformabilità controllando che l’abbassamento massimo dell’elemento non sia maggiore di 1/250 della luce. Questo procedimento si effettua allo Stato Limite di Esercizio in quanto ci interessano spostamenti e deformazioni della trave, azioni che possono compromettere l’uso e la funzione dell’edificio. Attraverso il foglio Excel calcoliamo la combinazione frequente allo SLE. 

 l/ v_max > 250   

Solaio incalcestruzzo armato

Il solaio analizzato è in latero cemento armato, con categoria di destinazione d’uso C2, cioè ambienti suscettibili di affollamento come i balconi o ballatoi.  

 

Peso proprio della struttura

q_s = 3,12 KN/m²

Peso portato dalla struttura:

q_p = 3,95 KN/m²

Carico accidentale:

q_a  = 4,00 KN/m²

Calcoliamo il carico totale attraverso una tabella Excel

KN/ m² (3,12 + 3,95 + (4,00 · 1,5)) 5,5 m =54,29 KN/m = q_u

Calcoliamo il momento massimo

M_max =  434,28 KNm

Una volta trovato il valore del momento massimo procediamo scegliendo il tipo di acciaio (nel nostro caso acciaio S450) e di calcestruzzo (C30) determinando i valori delle tensioni caratteristiche di progetto del calcestruzzo f_cd e quella delle barre d’acciaio f_yd attraverso i valori della resistenza dei due materiali:

 f_cd = α_cc f_ck/g_c

f_yd = f_yk/g_m

Definendo ora la base della sezione e noti i valori delle tensioni di progetto calcoliamo l’altezza utile da sommare al copri ferro per ottenere l'altezza minima della sezione anche attraverso b e r.

Andiamo ora a verificare le dimensioni appena definite della sezione (40x60) aggiungendo il peso proprio della trave e ricontrollando l’abbassamento. 

 

Solaio in Legno

Peso proprio della struttura

q_s = 0,27 KN/m²

Peso portato dalla struttura:

q_p = 2,74KN/m²

Carico accidentale:

q_a  = 4,00 KN/m²

E procediamo inserendo il valore caratteristico a flessione del legno che scegliamo in base alla classe di resistenza f_mk, il coefficiente parziale di sicurezza g_M, e il coefficiente diminutivo del valore di resistenza. Attraverso questi valori calcoliamo la tensione di progetto f_d.                

Stabiliamo ora la misura della base, e troviamo attraverso la formula l’altezza minima che dovrà avere la nostra sezione.

Una volta trovata l’altezza minima la sezione ingegnerizzata risulta essere di 60x65 cm.

In questo caso il peso proprio della trave in legno non viene considerato in quanto è un materiale leggero.

 

Solaio in Acciaio

Peso proprio della struttura

q_s = 2,55 KN/m²

Peso portato dalla struttura:

q_p = 3,45 KN/m²

Carico accidentale:

q_a  = 4,00 KN/m²

In base hai carichi calcolati, troviamo il momento massimo e scegliamo il tipo di acciaio: S355. 

Calcoliamo ora il modulo di resistenza a flessione -W_x- che deve essere minore di quello di progetto -W_d- e andiamo a scegliere il profilo della nostra IPE sul sagomario.

Il profilo adottato è un’IPE 500.

Verifichiamo ora che il rapporto tra la luce della trave e l’abbassamento massimo non sia superiore a 250, come prevede la normativa. 

Per calcolare l’abbassamento quindi aggiungo al -q_u- il peso proprio della trave data dal sagomario, calcolato nella combinazione allo SLE -q_e-, definisco il modulo elastico del materiale -E- e il momento d’inerzia -I-.

Il profilo risulta essere verificato.

 

Per la seconda esercitazione dobbiamo occuparci del dimensionamento della trave di un solaio realizzato con tre tecnologie diverse: in legno, in acciaio e in calcestruzzo.

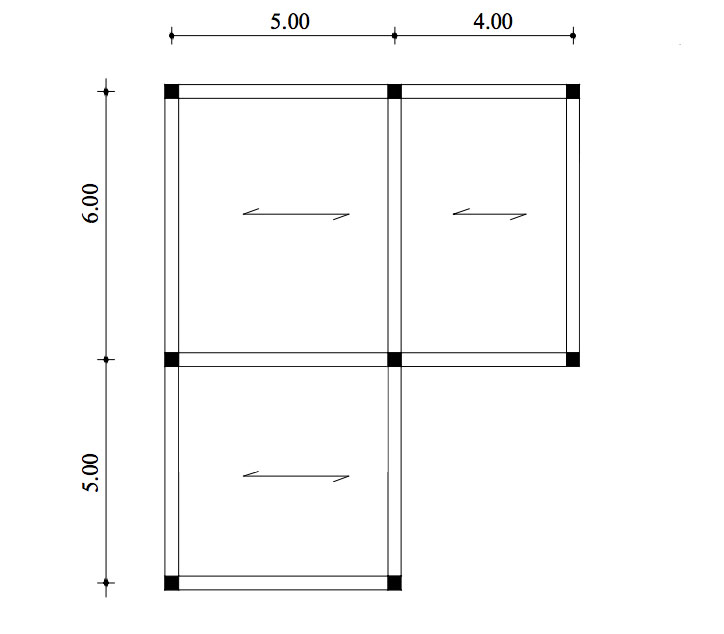
Scelto lo schema di un telaio piano con interasse variabile, dobbiamo innanzitutto, predimensionare le travi, in base alla luce e alla funzione che devono svolgere, cioè in base ai carichi che devono sostenere durante tutta la vita dell’opera.

Individuiamo quindi la gerarchia delle travi e l’area d’influenza della trave maggiormente sollecitata (con il maggior carico a metro lineare di trave), ricordandoci che a parità di area d’influenza si considera la trave con la luce maggiore.

Per ognuna delle tecnologie costruttive procediamo con l’analisi dei carichi agenti sul solaio, che si dividono in carichi strutturali - q_s -,  carichi permanenti - q_p - (azioni agenti sulla struttura) e carichi accidentali -q_a- (azioni agenti sulla struttura che variano sensibilmente nel tempo, queste azioni dipendono anche dalla destinazione d’uso dell’opera). Questi carichi vengono poi moltiplicati per dei coefficienti di combinazione, che aumentano il margine di sicurezza della struttura, che possiamo trovare nella normativa (NTC2008-Norme tecniche per le costruzioni – D.M. 14 Gennaio 2008). Hai fini della nostra esercitazione consideriamo la combinazione fondamentale allo stato limite ultimo.

 Andiamo ora a calcolare i vari carichi 

Solaio in cls:

Il solaio analizzato è in latero cemento armato, con destinazione residenziale

Peso proprio della struttura:

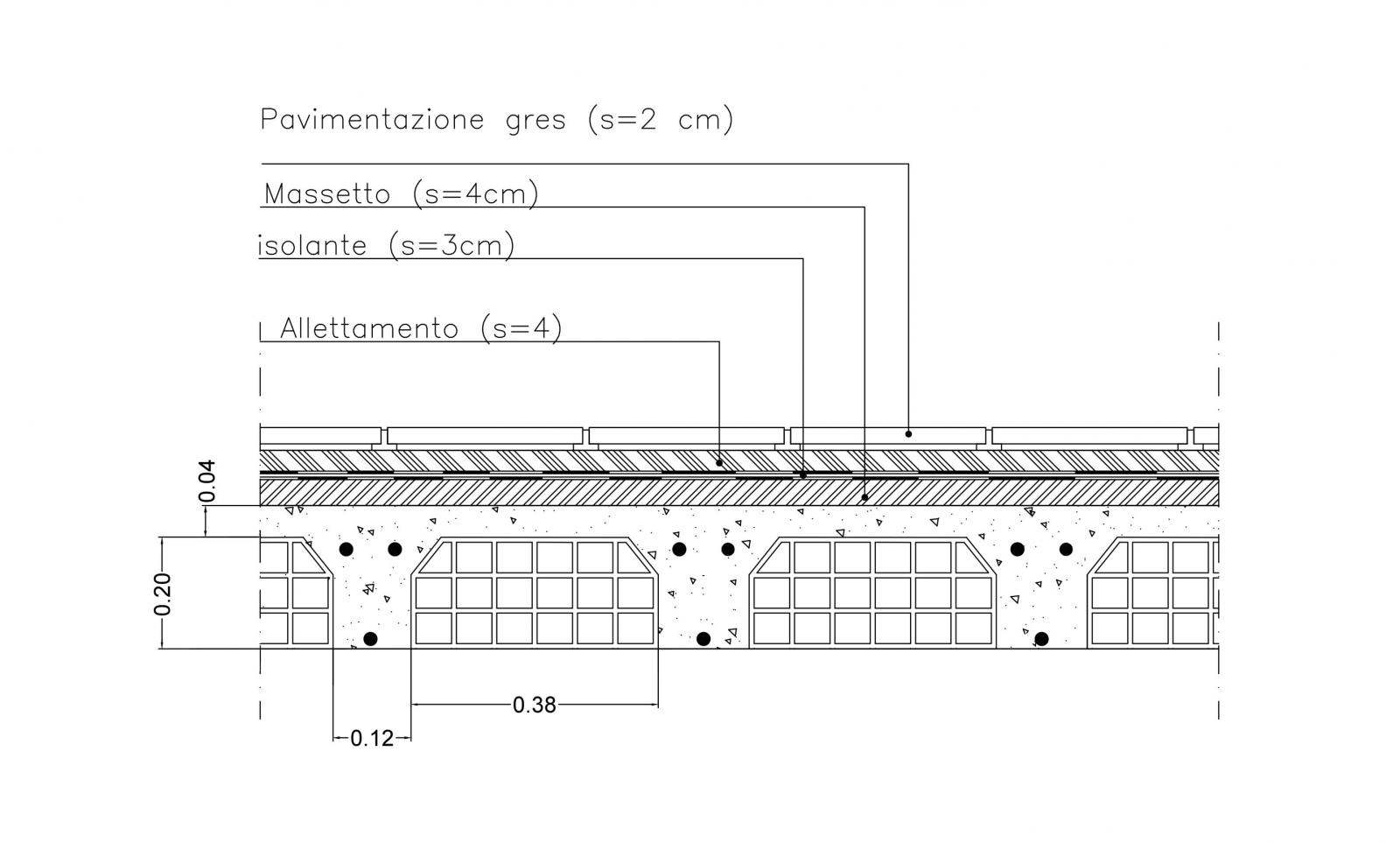
soletta in cemento armato _ 0,4 m · 25 KN/m³ = 1 KN/m² 

travetti _ 0,12 m (0,24 - 0,04)m · 25 KN/m³ = 1,2 KN/m²

pignatte _ 0,38 m (0,24 - 0,04)m · 6 KN/m³ = 0,92 KN/m²

q_s = 3,12 KN/m²

 

Peso portato dalla struttura:

pavimento piastrelle _ 0,02 m × 20 KN/m³ = 0,4 KN/m² 

allettamento _ 0,04 m · 20 KN/m³ = 0,8 KN/m² 

massetto _ 0,04 m · 18 KN/m³ = 0,72 KN/m² 

isolante _ 0,03 KN/m² 

intonaco _ 0,02 m · 20 KN/m³ = 0,4 KN/m² 

incidenza tramezzi  1,6 KN/m² 

q_p = 3,95 KN/m²

 

Carico accidentale:

cat A. – civile abitazione q_a  = 2,00 KN/m²

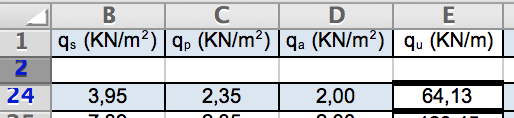
Calcoliamo il carico totale attraverso una tabella Exel

(KN/ m²(3,95 · 1,3) + (2,35 · 1,5) + (2,00 · 1,5)) 5,5 m = 64,13 KN/m = q_u

Possiamo ora procedere con il calcolo del momento massimo, che è dato dal prodotto del carico totale q_u per la luce al quadrato tutto diviso 8

M_max= ql²/8= 200,4 KNm

Una volta trovato il valore del momento massimo procediamo scegliendo il tipo di acciaio e di calcestruzzo determinando i valori delle tensioni di progetto del calcestruzzo f_cd e quella delle barre d’acciaio f_yd attraverso i valori della resistenza dei due materiali:

 f_cd = α_cc f_ck/g_c

f_yd = f_yk/g_m

Definendo ora la base della sezione e noti i valori delle tensioni di progetto calcoliamo l’altezza utile da sommare al copri ferro per ottenere l'altezza minima della sezione anche attraverso b r che sono rispettivamente

b= f_cd/ (f_cd+( f_yd/n))

r=(2/(f_cd(1-(b/3)b))^1/2

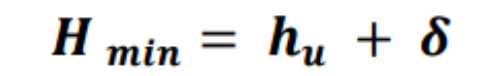
Il peso proprio della trave ci permette di verificare se la sezione da noi scelta è in grado di portare i carichi precedentemente calcolati. Per verificarlo dobbiamo sommare al carico totale q_u il peso proprio appena calcolato moltiplicato per il relativo fattore di sicurezza e rifare i calcoli. 

Se l'H_min dovesse risultare maggiore dell'H ingegnerizzata bisognerà rivedere l'altezza utile della sezione.

 

Solaio in legno:

Il solaio preso in esame è un solaio realizzato con travi principali con interasse maggiore pari a 5,5m con dei travetti 10x10cm disposti trasversalmente.

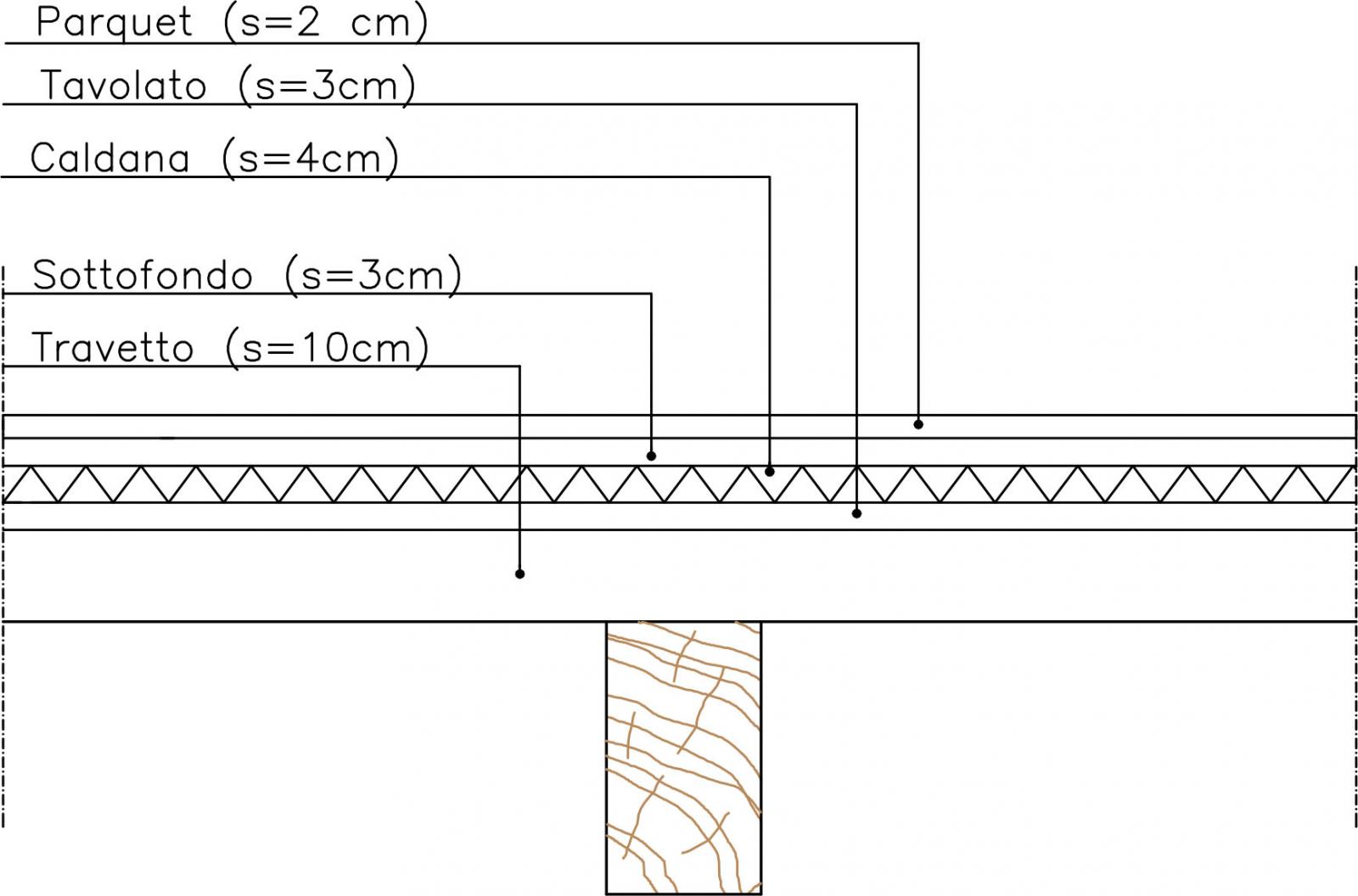
Analisi dei carichi

Peso proprio della struttura:

travetti _ (0,1 × 0,1 × 1)m 6 KN/m³ = 0,06 KN/m²

tavolato _ 0,03 m × 18 KN/m³ = 0,21 KN/m² 

q_s = 0,27 KN/m²

 

Peso portato dalla struttura:

parquet _ 0,02 m × 7,5 KN/m³ = 0,15 KN/m² 

sottofondo _ 0,03 m × 18 KN/m³ = 0,54 KN/m² 

caldana _ 0,04m × 21KN/m³ = 0,84 KN/m² 

incidenza tramezzi _ 1 KN/m² 

q_p = 2,74 KN/m²

 

Carico accidentale:

cat A. – civile abitazione q_p  = 2,00 KN/m²

Una volta calcolato il carico totale, troviamoci il momento massimo della nostra trave doppiamente appoggiata, sempre attraverso il foglio Excel.

M_max= ql²/8= 114,13 KNm

Procediamo inserendo il valore caratteristico a flessione del legno (che si differenzia da quello della resistenza a trazione o compressione, in quanto non è un materiale che reagisce allo stesso modo nelle diverse direzioni) scelto in base alla classe di resistenza. Nel  nostro caso utilizziamo il valore del legno lamellare.

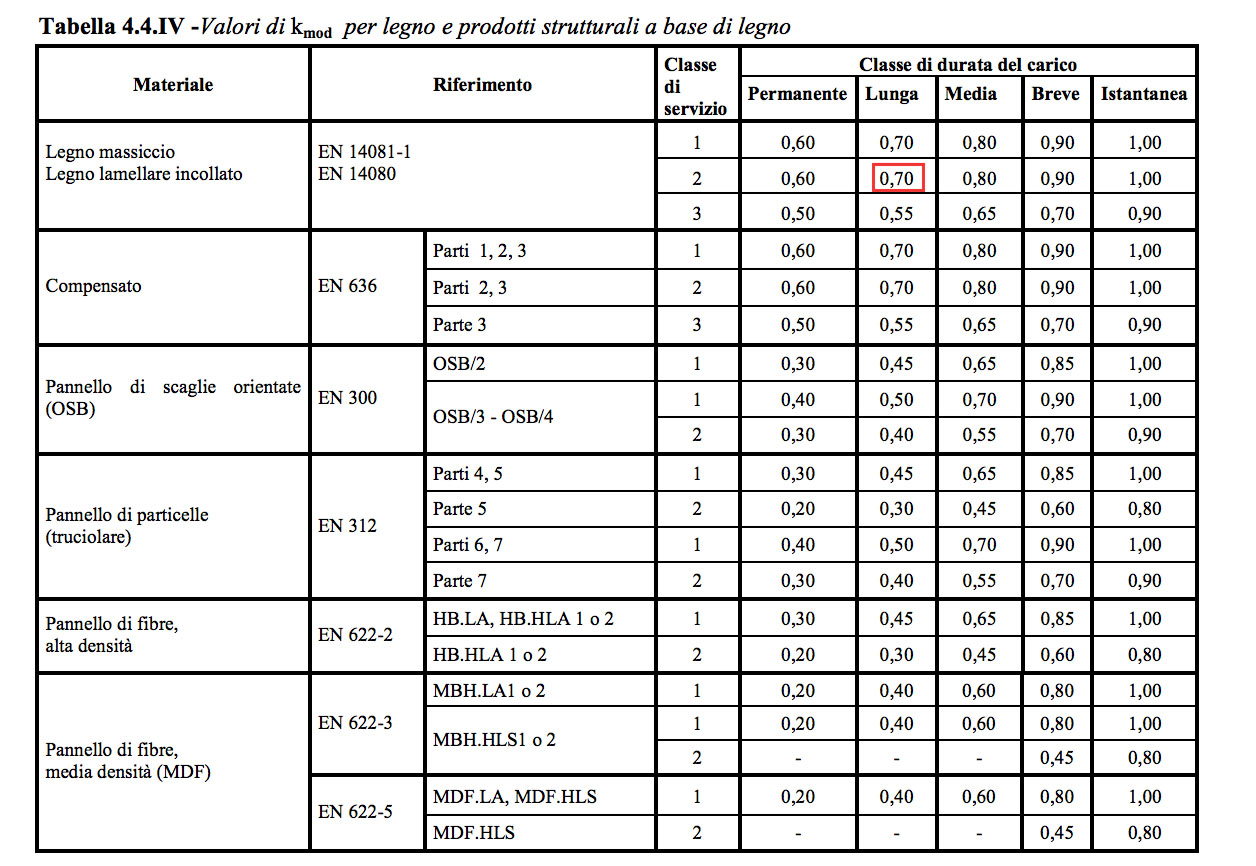
La resistenza caratteristica del materiale f_mk insieme al coefficiente parziale di sicurezza del materiale γ_M e

 al coefficiente diminutivo del valore di resistenza k_mod, che tiene conto dell’effetto della durata del carico e delle condizioni in cui la struttura si andrà ad inserire, ci permettono di ricavare la tensione di progetto f_d, in base al materiale prescelto.  

Ricavata la tensione di progetto procediamo determinando una dimensione della base della sezione e andiamo a calcolare l’altezza minima:

 

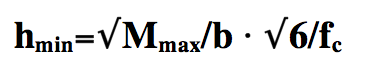
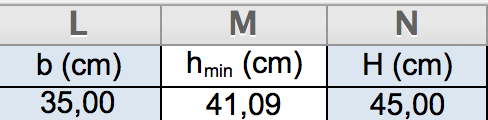
Una volta trovata l’altezza minima la sezione va ingegnerizzata cioè va scelto un valore superiore all’altezza minima

che sia compatibile con i profili esistenti sul mercato.

La trave adottata avrà dimensioni 35x45 cm

 

Solaio in acciaio:

Analisi dei carichi

Peso proprio della struttura:

travetti secondari IPE 140 _ 12,9 Kg/m _ 0,129 KN/m²

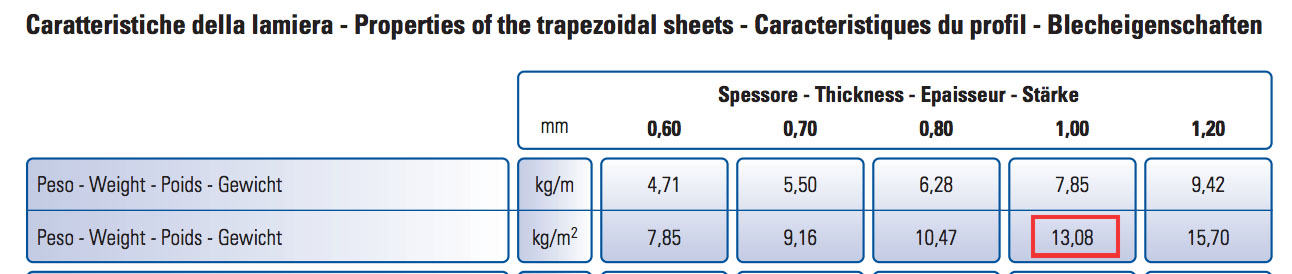
lamiera grecata s=1 mm _ 13,08 Kg/m² = 0,13 KN/m² 

 

soletta in c.a. s = 0,065 + (0,055/2) = 0,0925 m _ 25 KN/m³ × 0,0925 = 2,31 KN/m² 

q_s = 2,55KN/m²

 

Peso portato dalla struttura:

pavimento piastrellato _ 0,02 m × 20 KN/m³ = 0,15 KN/m² 

massetto _ 0,1 m × 19 KN/m³ = 1,9 KN/m² 

controsoffitto _ 0,40 KN/m²

incidenza tramezzi _ 1 KN/m² 

q_p = 3,45 KN/m²

 

Carico accidentale:

cat A. – civile abitazione q_a  = 2,00 KN/m²

Una volta calcolato il carico e il momento massimo scegliamo il tipo di acciaio, nel nostro caso acciaio S275 che quindi avrà come tensione di snervamento caratteristica del materiale f_yk = 275 Mpa.  

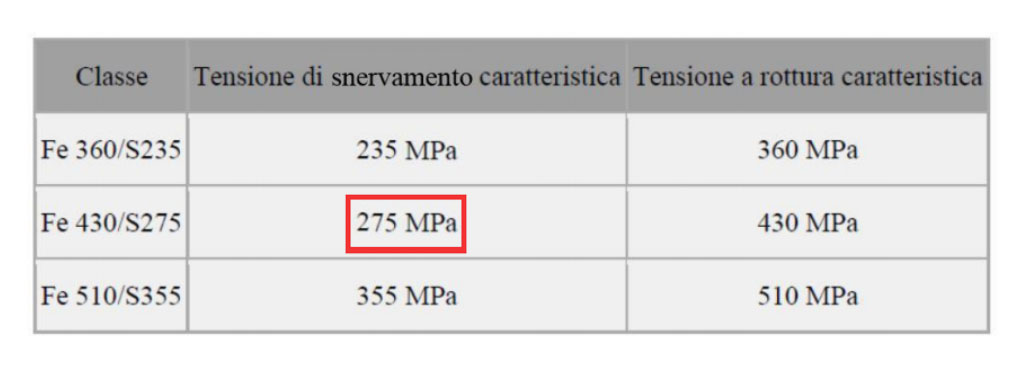
Calcolata poi la tensione di progetto applichiamo la formula di Navier per ricavare il modulo di resistenza a flessione W_x. che ci serve per sapere il valore minimo che può avere la nostra sezione.

Andiamo ora sul sagomario e scegliamo un valore di resistenza maggiore e ingegnerizzato rispetto a quello trovato. 

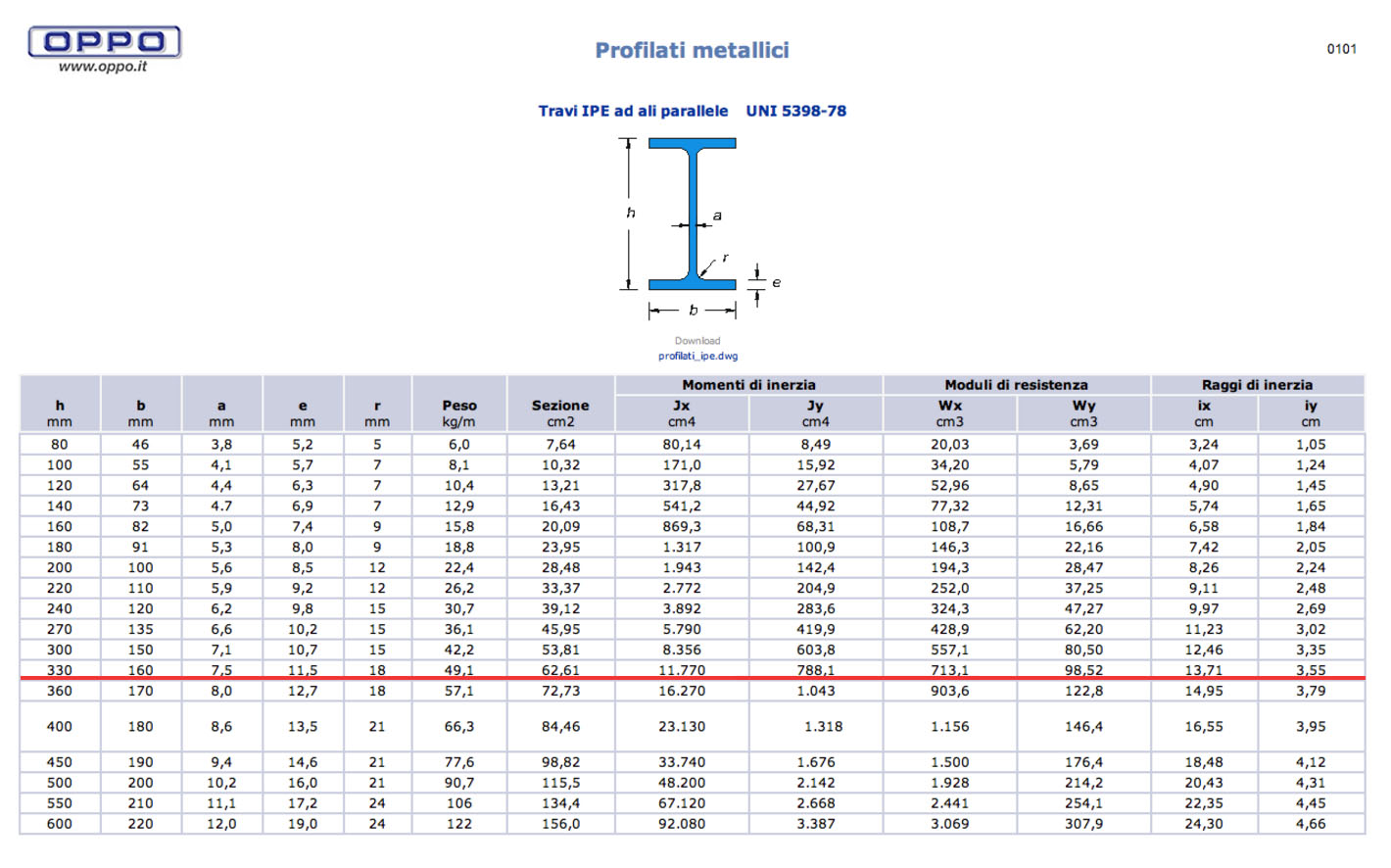
La trave adottata sarà un IPE 330