Es_4 Ripartizione forza sismica

Questa esercitazione è finalizzata a calcolare come viene ripartita una forza orizzontale, come può essere il vento o il sisma, su un generico impalcato strutturale ad un piano. Calcoleremo quindi le rigidezze dei controventi, il centro d’area e il centro delle rigidezze dell’impalcato trovando così gli spostamenti prodotti dalla forza.

L’impalcato preso in considerazione è costituito da telai piani in cemento armato con controventi di tipo Shear-type, la cui caratteristica è di avere travi infinitamente rigide questo fa sì che ai pilastri non vengano trasmesse rotazioni.

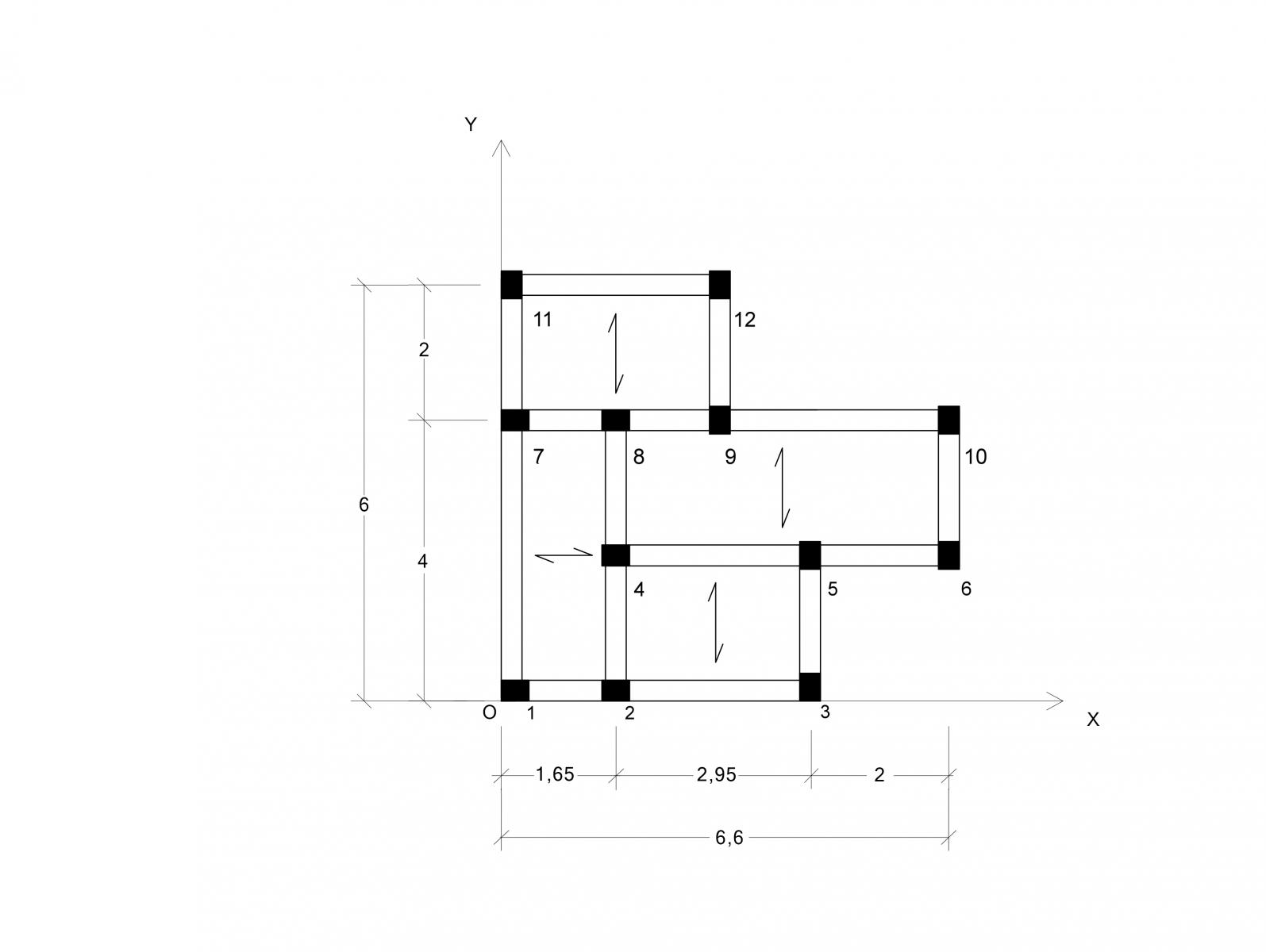
Per prima cosa poniamo l’impalcato in un sistema di riferimento cartesiano dove andiamo ad individuare i telai paralleli all’asse y e quindi verticali e i telai paralleli all’asse x quindi orizzontali:

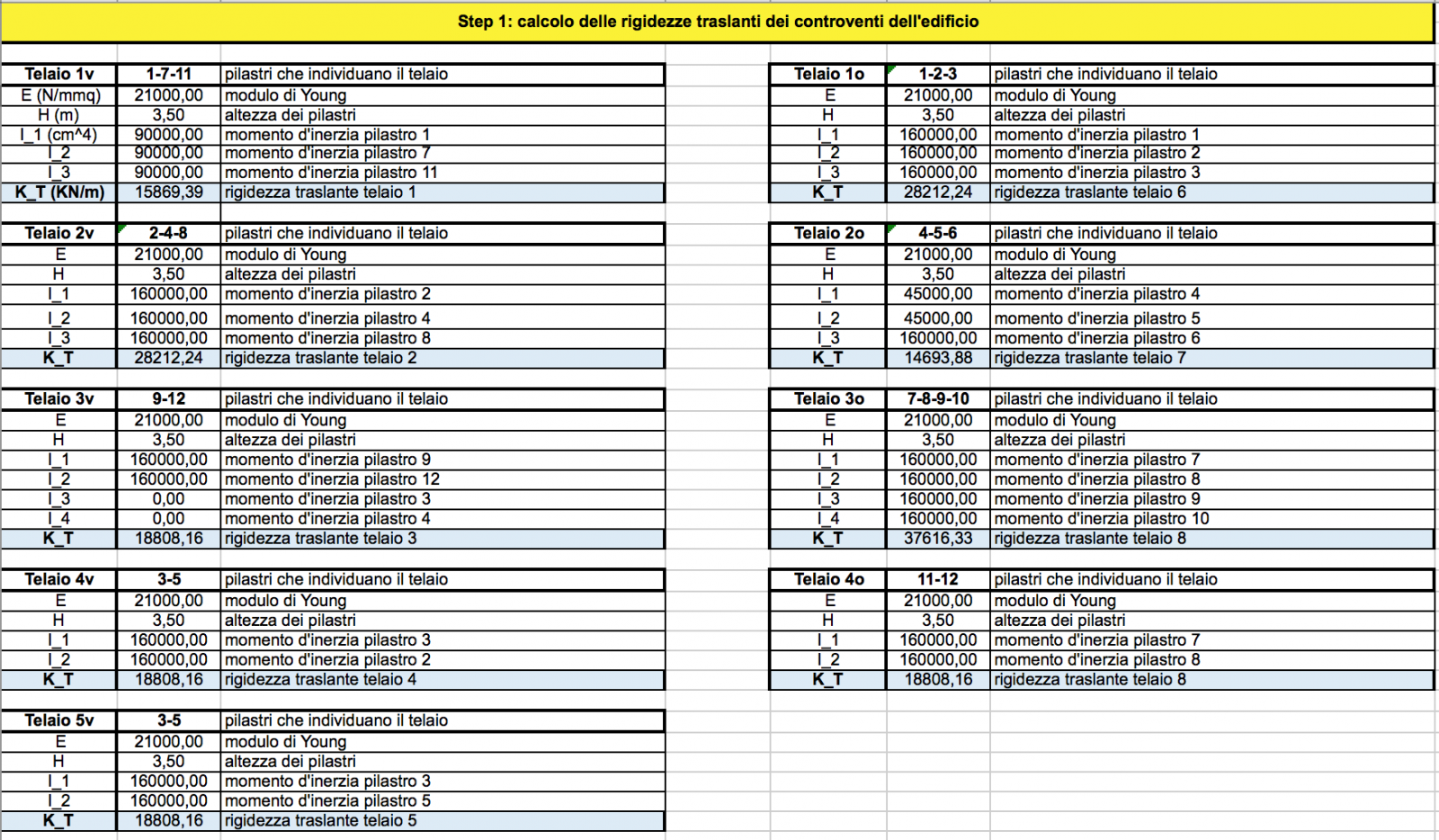
Telaio 1v  composto da: pilastri  1, 7 e 11

Telaio 2v  composto da: pilastri  2, 4 e 8

Telaio 3v  composto da: pilastri  9 e 12

Telaio 4v  composto da: pilastri  3 e 5

Telaio 5v  composto da: pilastri  6 e 10

 Telaio 1o composto da: pilastri  1, 2 e 3

 Telaio 2o composto da: pilastri  4, 5 e 6

 Telaio 3o composto da: pilastri  7, 8, 9 e 10

 Telaio 4o composto da: pilastri  11 e 12

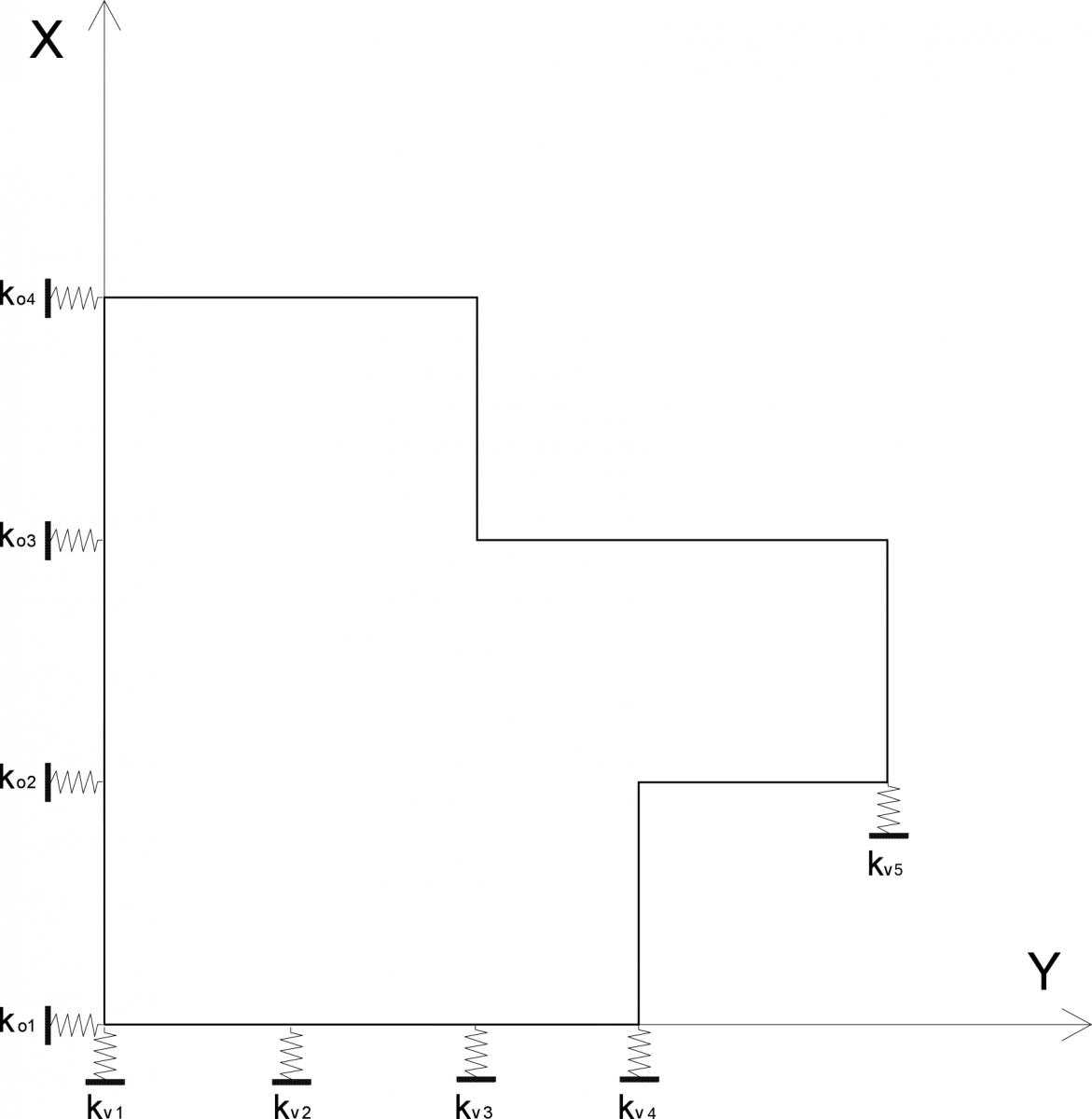
I controventi, che per il solaio rappresentano vincoli cedevoli elasticamente, possono essere schematizzati nel piano dell'impalcato come molle, aventi un’adeguata rigidezza.

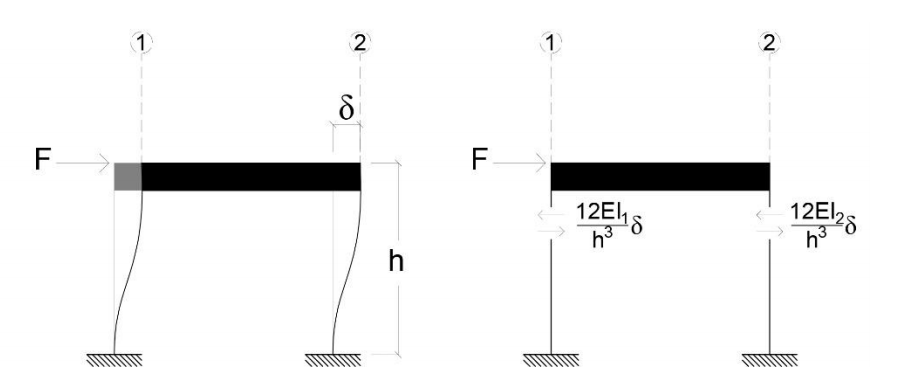
Trattandosi di telai shar-type la loro rigidezza sarà data da:

Quindi in generale per un telaio di n pilastri la rigidezza sarà: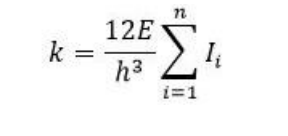 

Dove E rappresenta il modulo elastico del cls armato mentre I è il momento d’inerzia del pilastro secondo la direzione in cui resiste meglio. 

quindi per il pilastro da noi adottato avremo: 

Iy=(30*40^3)/12=160000

Ix=(40*30^3)/12=9000

Andiamo ora a calcolare la rigidezza traslante associata ad ogni controvento sapendo che l’altezza di ogni nostro pilastro è di 3,5 m e il modulo elastico del nostro materiale  è di 21000 N/mm^2.

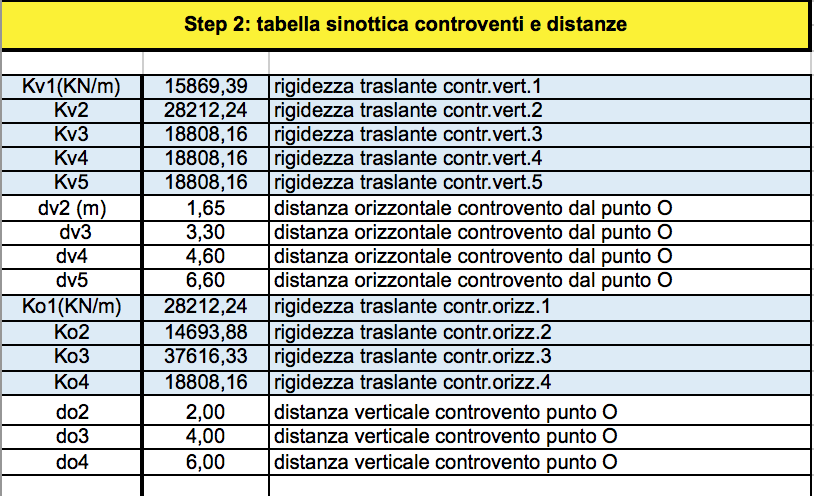
Una volta definita la rigidezza di ogni controvento le riportiamo in tabella insieme alla sua distanza dall’origine. 

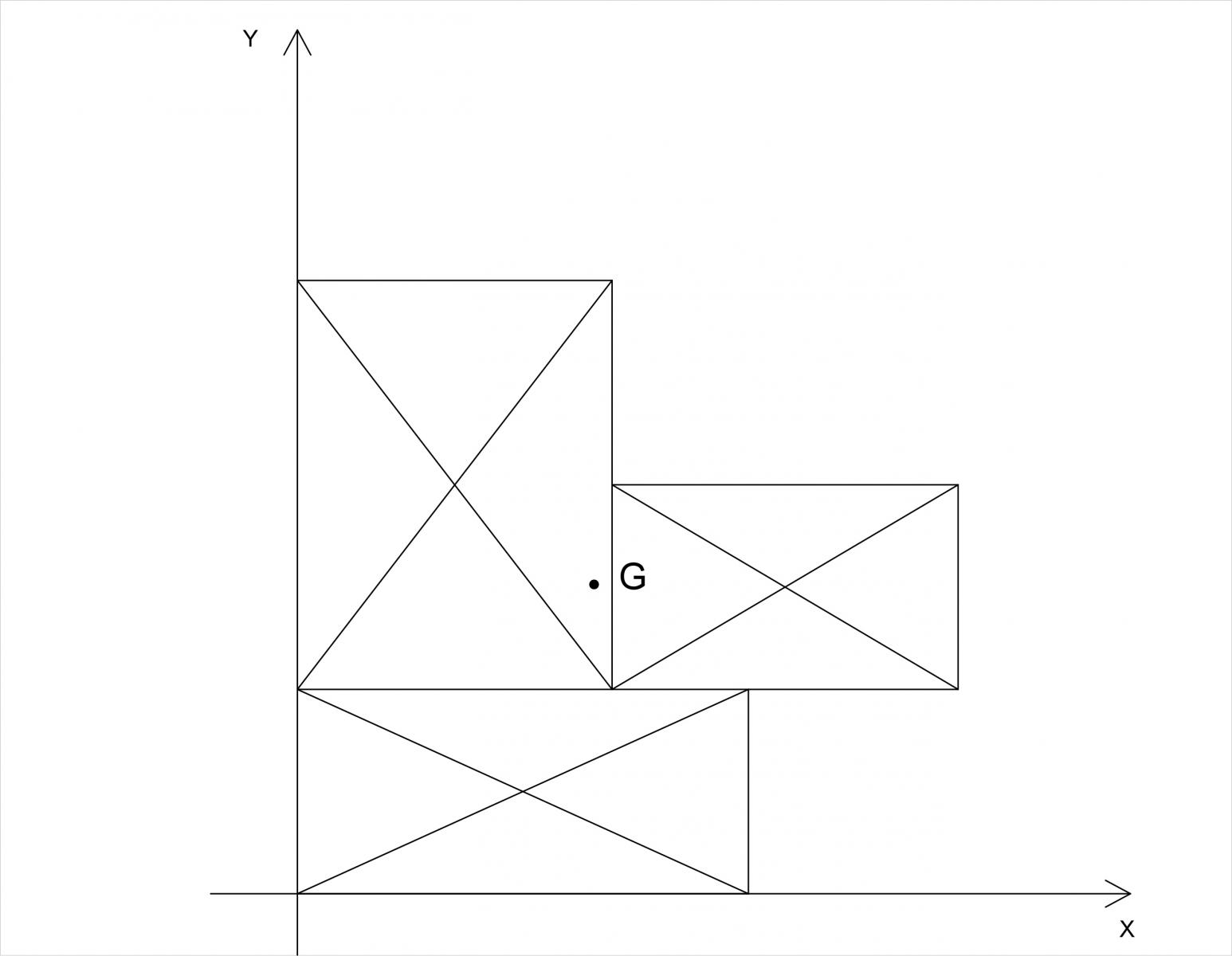
Ora vediamo come calcolare il centro di massa dell’impalcato (G).

Innanzi tutto dividiamo l’impalcato in forme geometriche elementari come i rettangoli, nel nostro caso tre, di cui definiamo l’area e il baricentro:

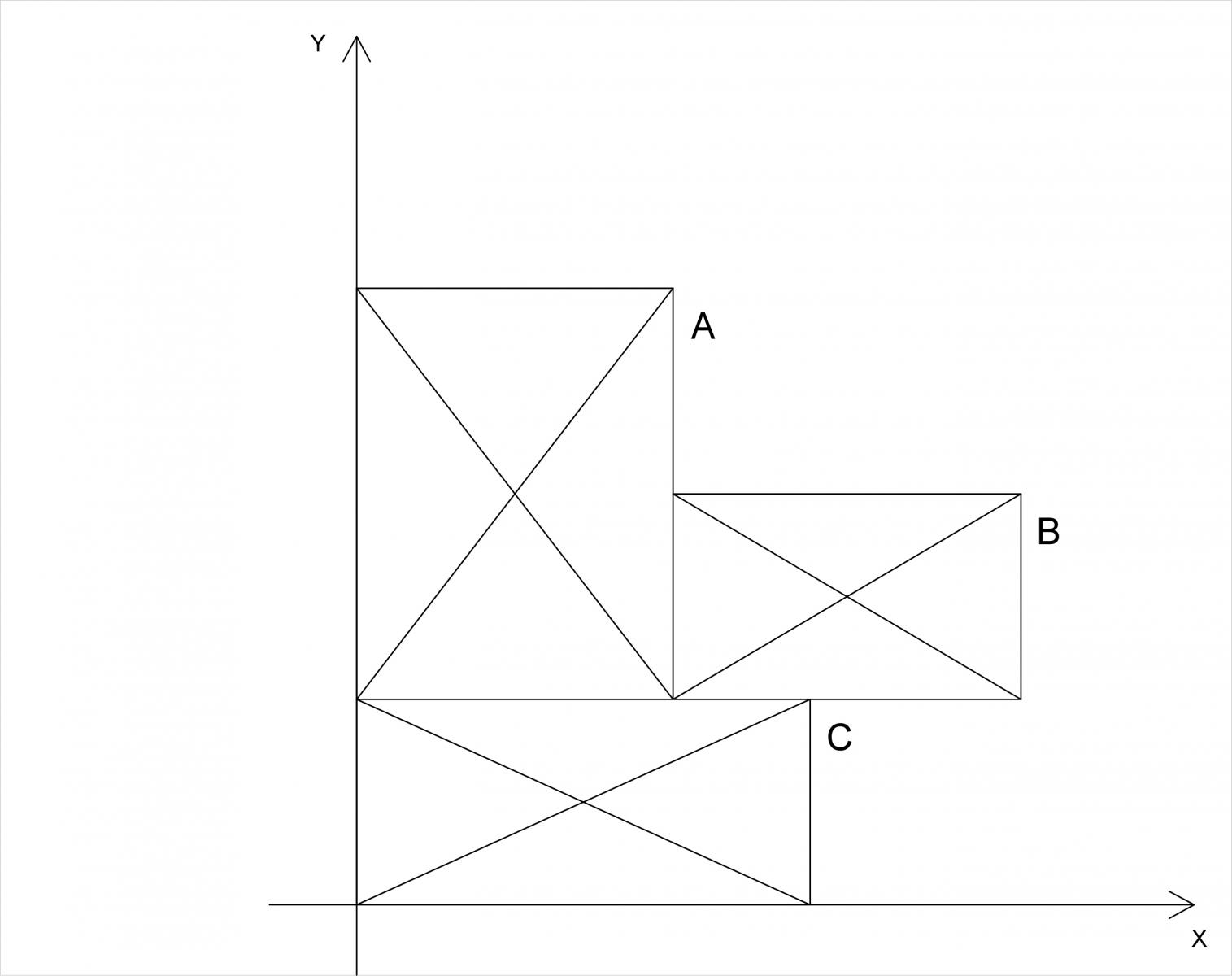
Area A: 11,70 m²

Area B: 6,43 m²

Area C:  8,43 m²

Centro A: (1,5 ;  3,9)

Centro B: (4,6 ;  2,9)

Centro C: (2,5 ;  0,97)

Applichiamo ora attraverso il foglio Excel la formula della sommatoria per trovare il centro di massa che risulta avere coordinate G (2,58 ; 2,73).

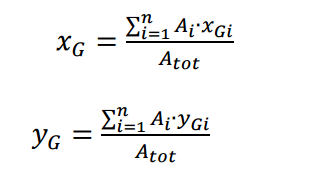
Definiamo ora le coordinate del centro delle rigidezze (Xc, Yc) attraverso la sommatoria che moltiplica le rigidezze traslanti  (kv, ko) per la distanza del controvento dall’origine (dv, do). 

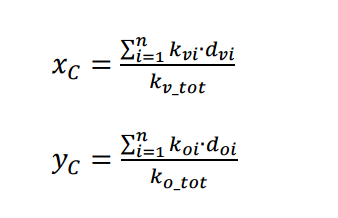
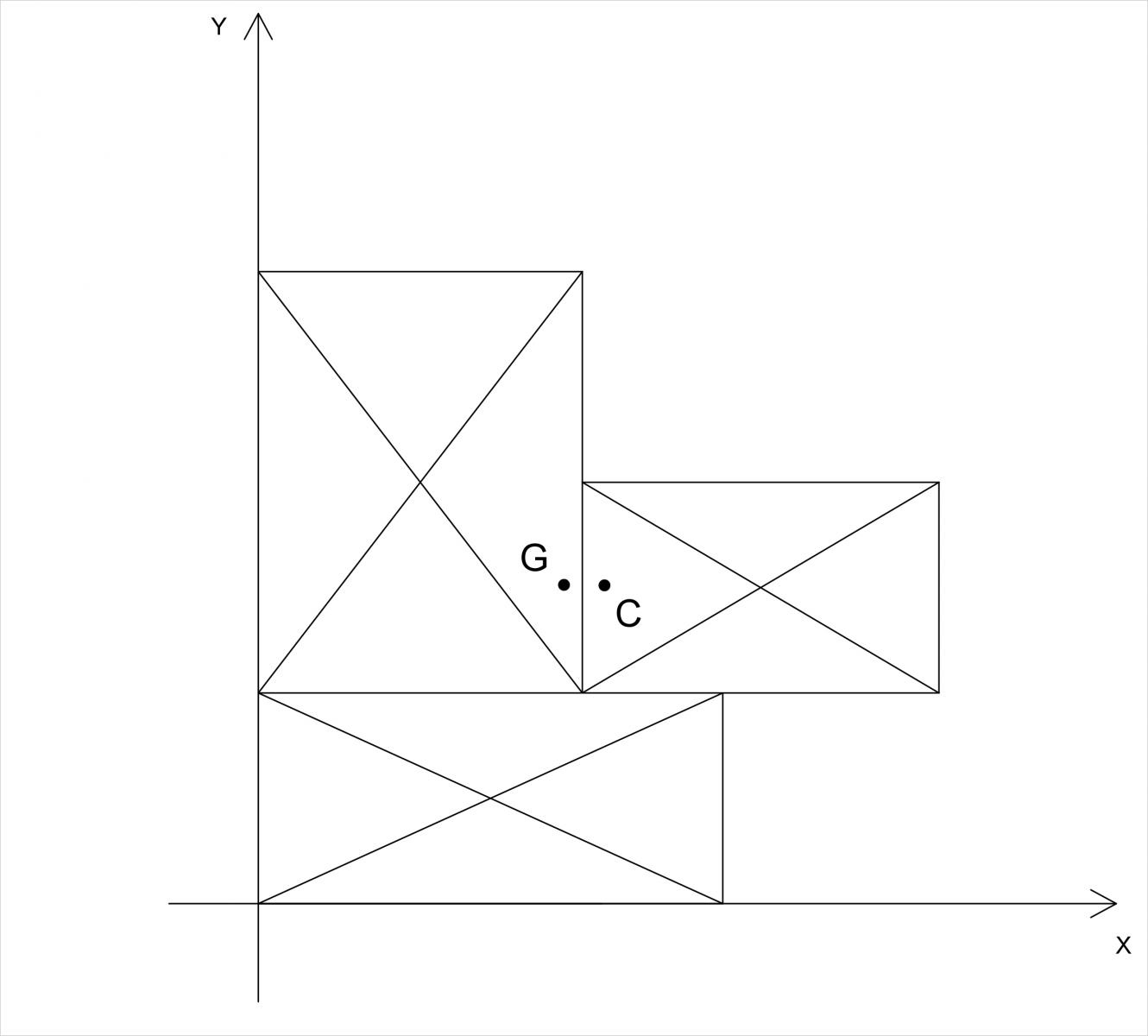
Ricaviamo ora il valore delle rigidezza torsionale calcolando tutte le distanze dei diversi controventi (ddv, ddo) dal centro delle rigidezze (C) data dalla formula:

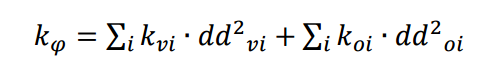
Nella tabella successiva possiamo calcolare il valore della forza sismica agente  sull’impalcato attraverso l’analisi dei carichi sismici.

Per far ciò riprendiamo i valori dei carichi strutturali, permanenti, e accidentali dell’esercitazione sul dimensionamento della trave:

q_s = 3,12 KN/m²

q_p = 3,95 KN/m²

q_p  = 2,00 KN/m²

Attraverso il foglio Excel e il valore dei carichi per unità di superficie (KN/mq) calcoliamo il carico totale permanete (G), il carico totale accidentale (Q) come segue: