Esercitazione IV: Ripartizione di una Forza sismica

Per questa quarta esercitazione vogliamo vedere gli effetti di una forza orizzontale (nello specifico una forza sismica) su di un telaio piano, utilizzando il metodo delle rigidezze e applicnado la forza come F_x e F_y lungo le coordinate x e y .

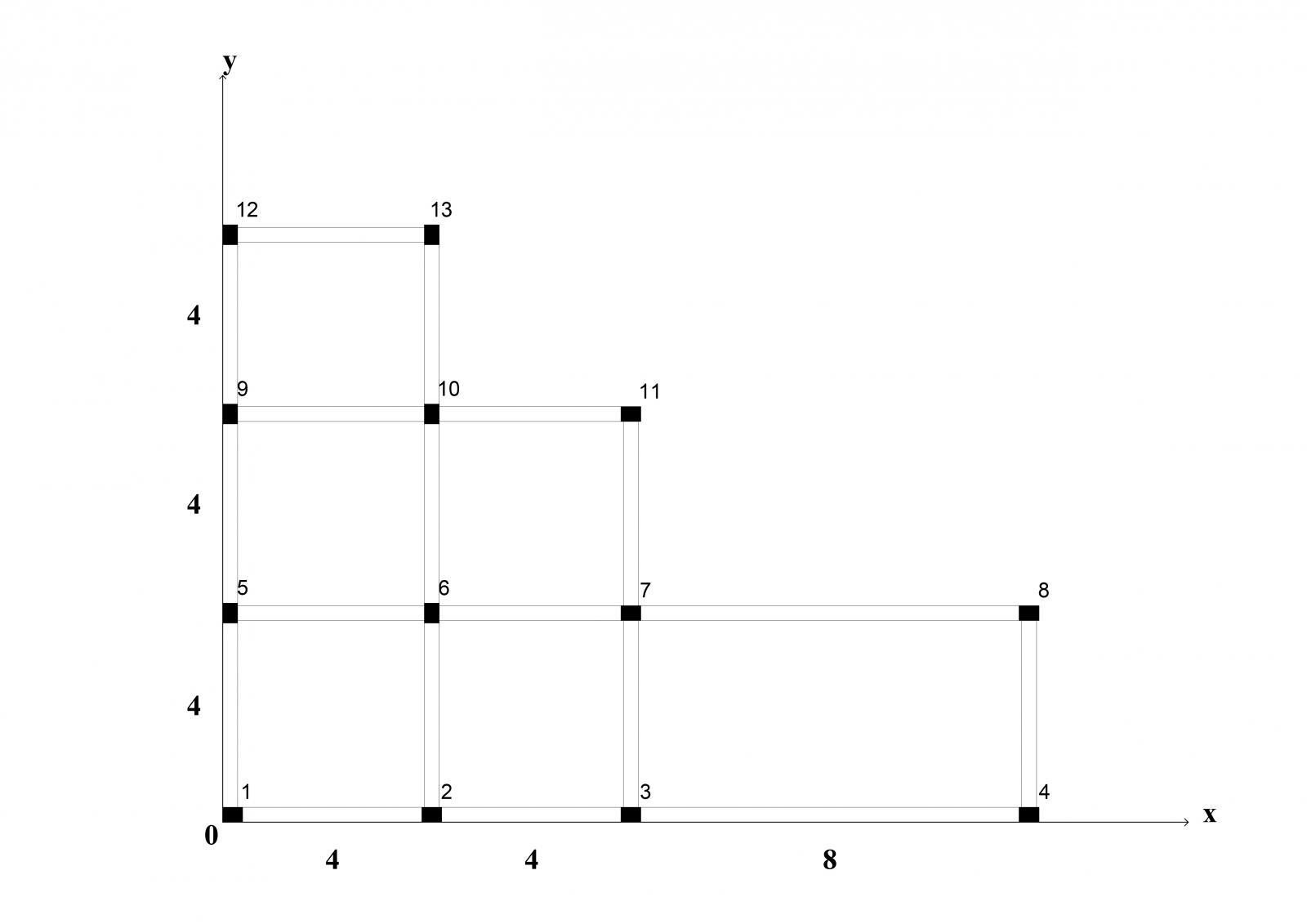
Prendiamo in esame l'impalcato di un solaio appartenente ad un edificio monopiano,  di cui la struttura sia composta da telai piani realizzati in cemento armato. Questo telaio non soltanto permette di scaricare a terra i carichi mediante il flusso di carico verticale, ma anche di sopportare le azioni orizzontali ( che possono,ad esempio, essere causate da vento o sisma), funzionando come veri e propri controventi. Per prima cosa dobbiamo individuare i telai che compongono il nostro impalcato: avremo 4 telai paralleli alla direzione x  e 4 paralleli a y

1v- Pilastri: 1-5-9-12              1o- Pilastri: 1-2-3-4

2v- Pilastri: 2-6-10-13            2o- Pilastri: 5-6-7-8

3v- Pilastri: 3-7-11                 3o- Pilastri: 9-10-11

4v- Pilastri: 4-8                      4o- Pilastri: 12-13

Il controvento può essere definito come un appoggio cedevole elasticamente, in quanto corpo rigido sul proprio piano che si oppone elasticamente ad una forza orizzontale applicata.La capacità del controvento di opporsi (più o meno) a questa forza è la sua rigidezza. Per questo motivo possiamo vedere questi controventi come molle

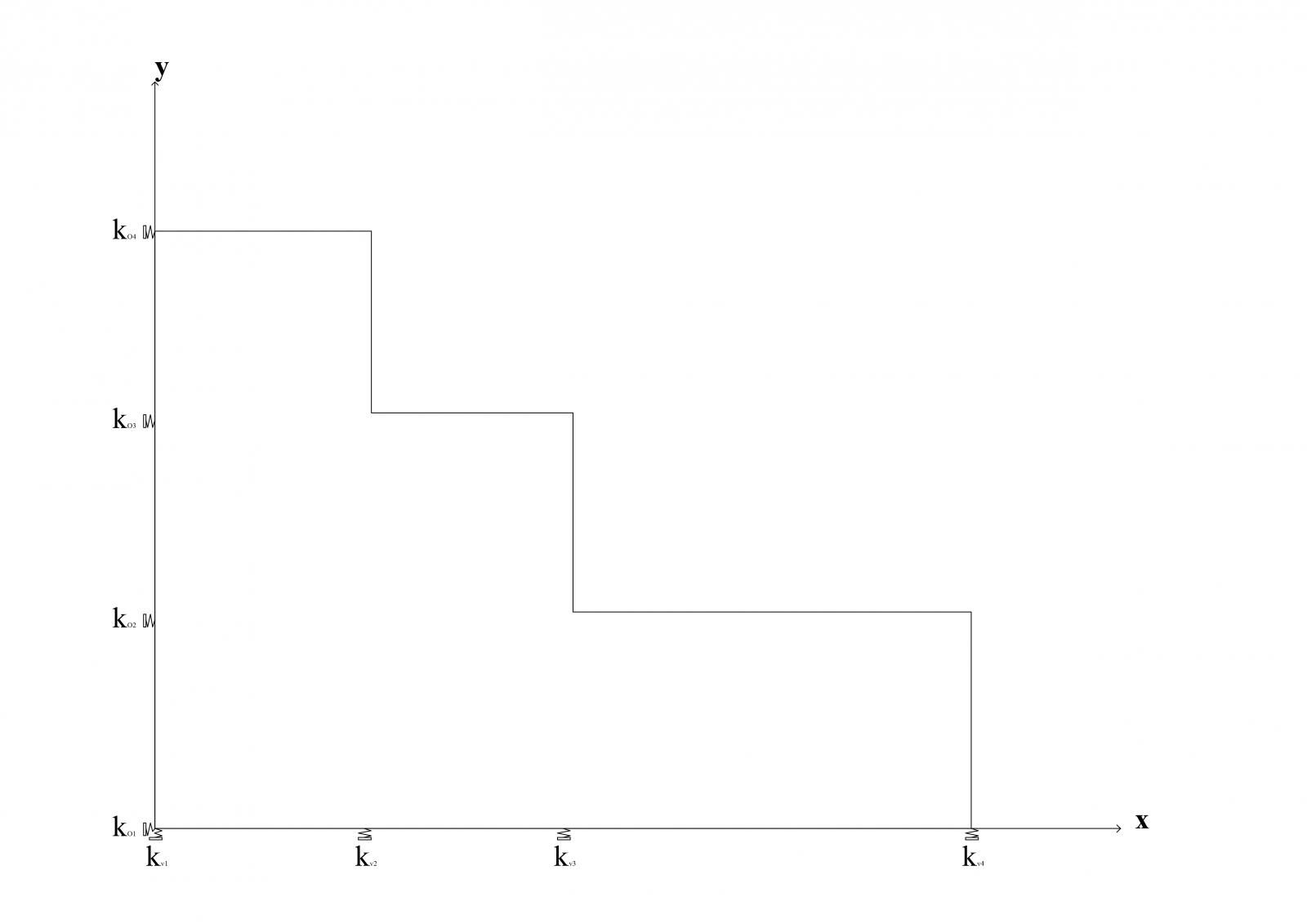Per questa esercitazione ipotizziamo che il telaio sia modellato come un telaio di tipo Shear-Type, la cui rigidezza traslante è:

Dobbiamo quindi tenere conto del modulo di elasticità E del materiale ( E c.a.= 21.000 MPa) e dei diversi Momenti di Inerzia legati alla forma della sezione del pilastro

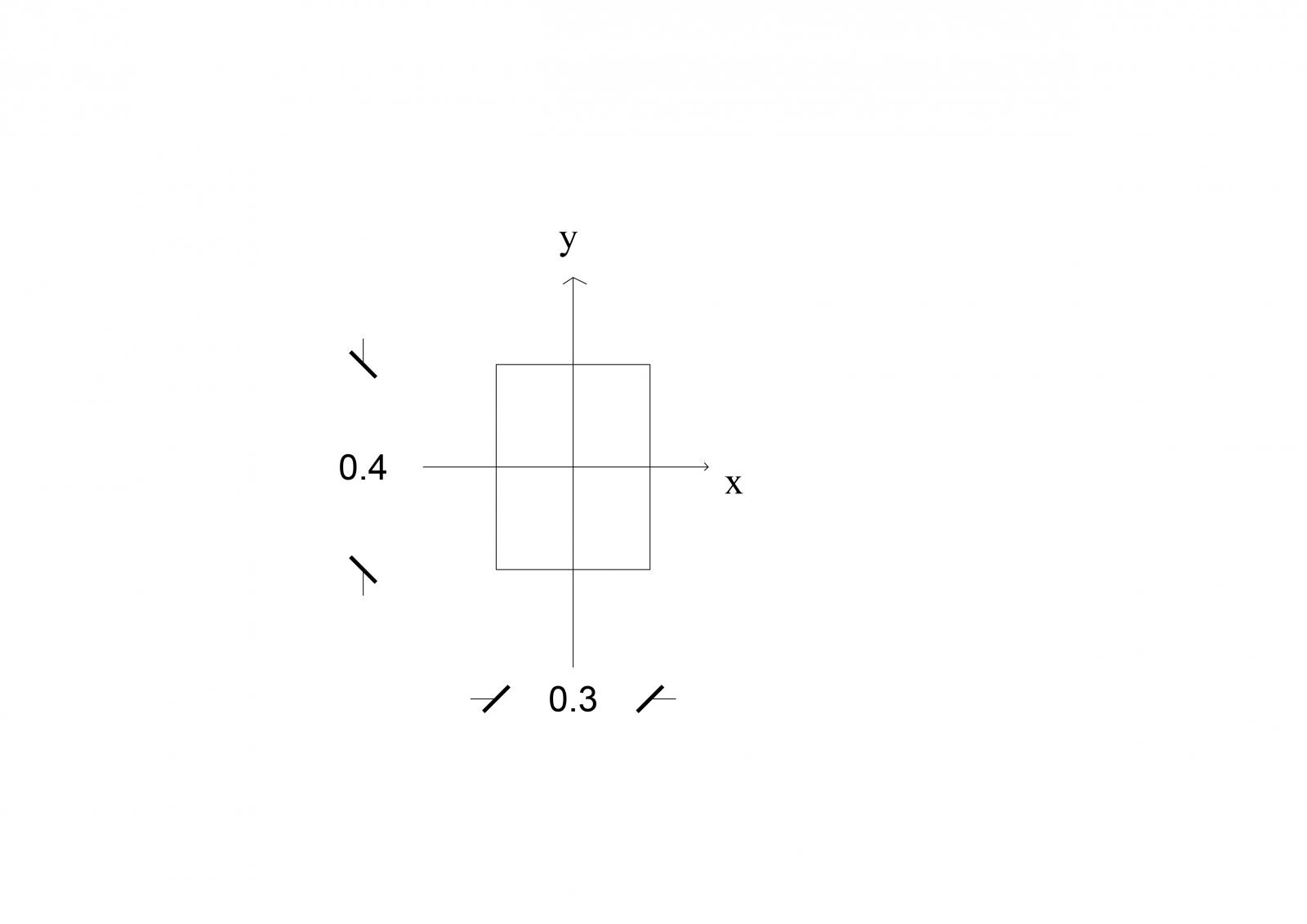
• I_x= (bh³)/12=160.000 cm⁴
• I_y= 90.000 cm⁴

Nello STEP1, calcoliamo la rigidezza traslante associata a tutti i controventi, in base alle altezze H al modulo di elasticità E e ai momenti d'inerzia I, come già anticipato:

Nello STEP2 viene riportata una tabella riassuntiva dei valori delle rigidezze traslanti e delle distanze dei controventi da un polo O, origine di un sistema di riferimento cartesiano da me scelto.

Con lo STEP 3 intendiamo calcolare le coordinate del centro di massa dell'impalcato; per far questo lo suddividiamo in 3 Aree rettangolari i cui centri di massa relativi sono più immediati da individuare. 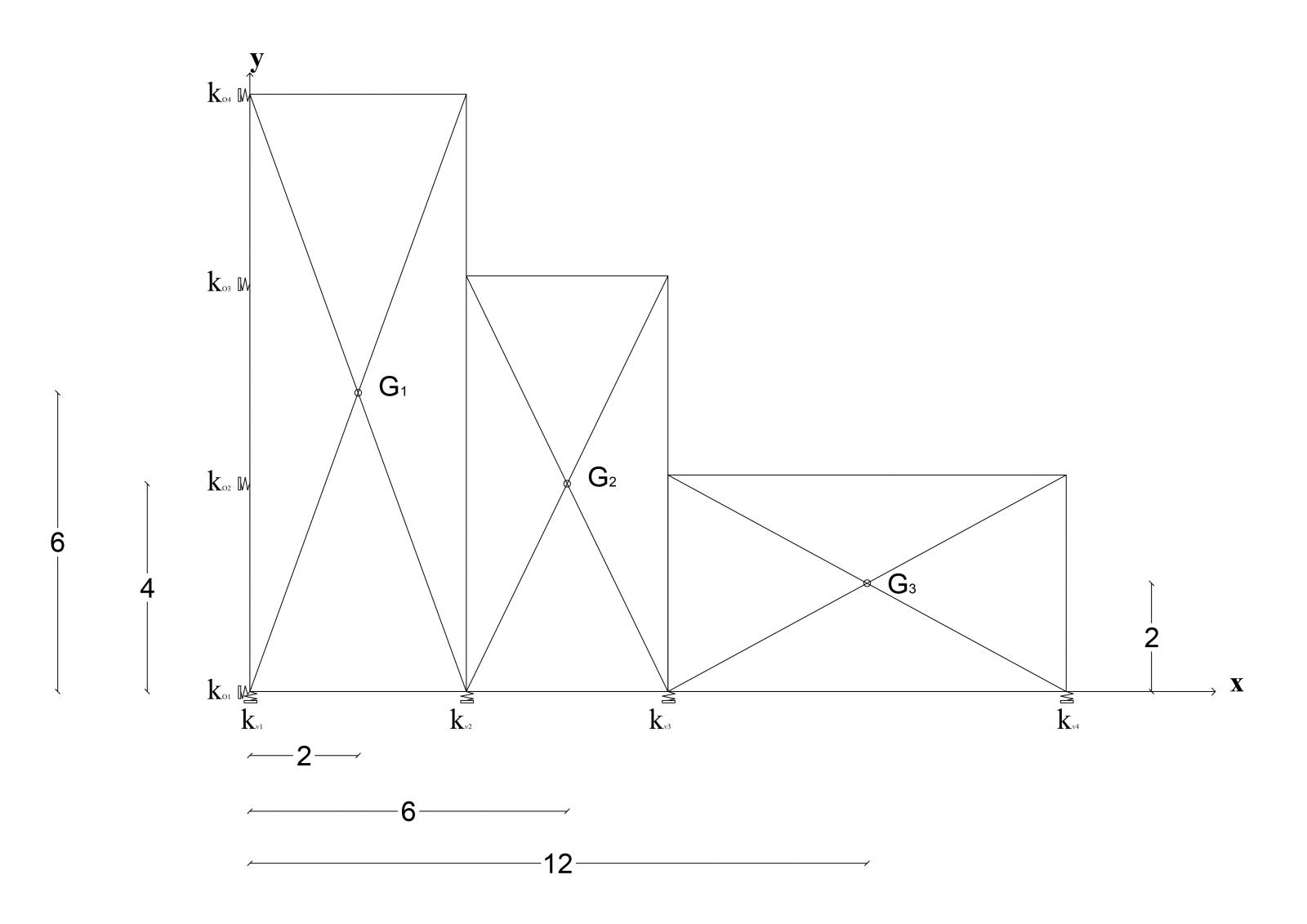Una volta noti questi, possiamo conoscere le coordinate x ed y di G grazie alla formula (derivata da quella per le coordinate del centro di un sistema di vettori paralleli:

Nello STEP 4 vengono calcolate le rigidezze totali sia verticale che orizzontale, nonché la rigidezza torsionale totale e il centro delle rigidezze come segue:

A questo punto possiamo applicare all'impalcato i centri di massa e rigidezza, confrontarne le posizioni relative e applicare una forza (sismica) orizzontale al centro di massa G per valutarne gli effetti cinematici.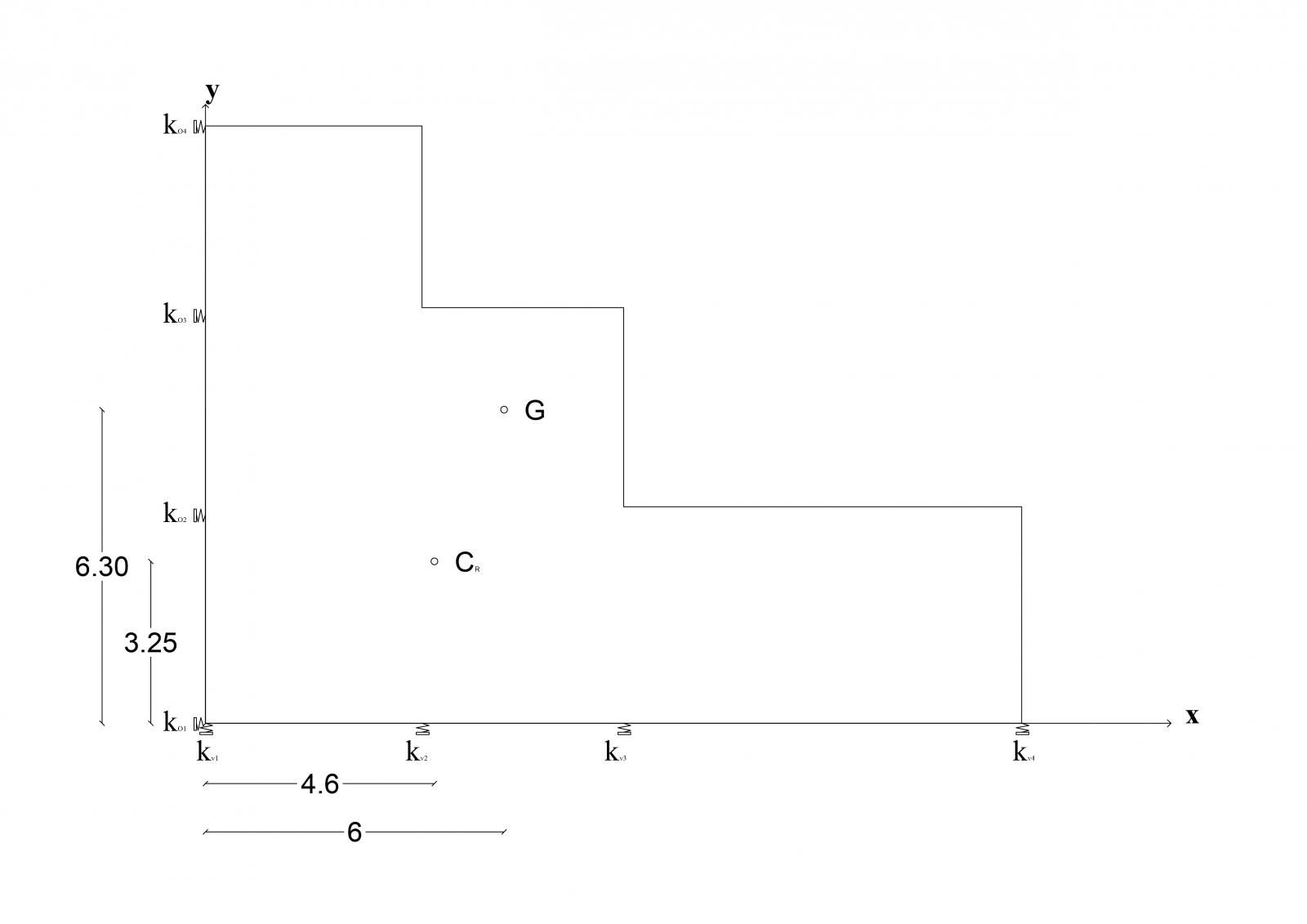

Come è possibile immediatamente evincere dall'immagine soprastante, i due centri non coincidono, il che vuol dire che applicando forze in entrambe le direzioni la nostra struttura subirà non solo una traslazione ma anche una rotazione, provocata da un momento di intensità pari a F applicata in G per la distanza tra i due centri (braccio).

Nello STEP 5 analizziamo i carichi gravanti sulla struttura per conoscere l'effetto del carico sismico, tenendo presente che il solaio ipotizzato è in latero-cemento per un ufficio aperto al pubblico ( CAT-B2); l'analisi prevede:

dove: -G= carichi permanenti; - Q= carichi variabili; W= peso sismico; psi= fattore di contemporaneità; c= coeff. intesità sismica; F= forza sismica orizzontale

Infine, negli STEP 6 e 7 passiamo alla valutazione degli effetti cinematici della forza orizzontale, rispettivamente orientata lungo x e lungo y. Come già detto, prevediamo di avere sia traslazioni che rotazioni in entrambi i casi, in quanto i due centri C e G non combaciano.

-Effetti di forze orizzontali lungo x ed y: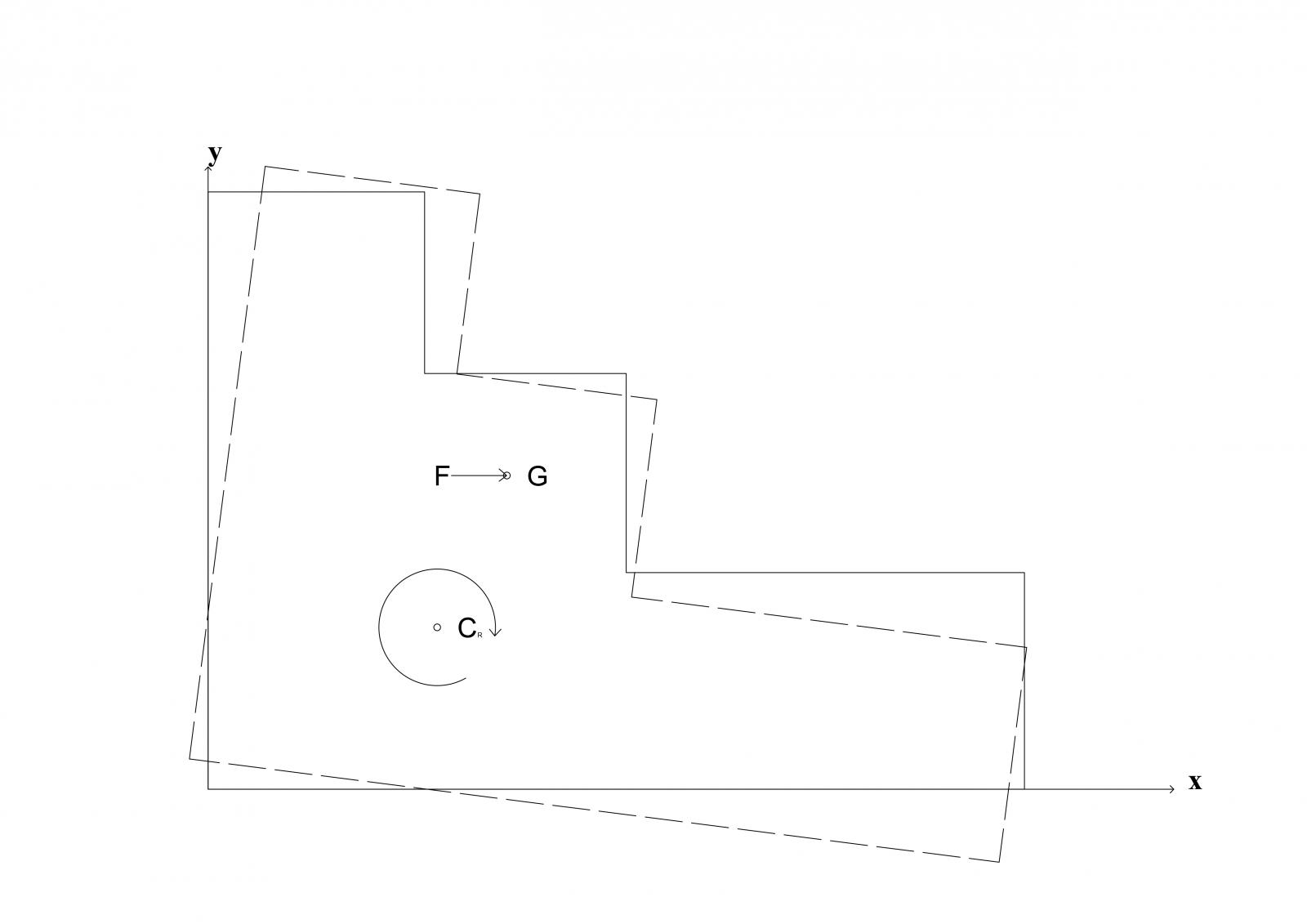

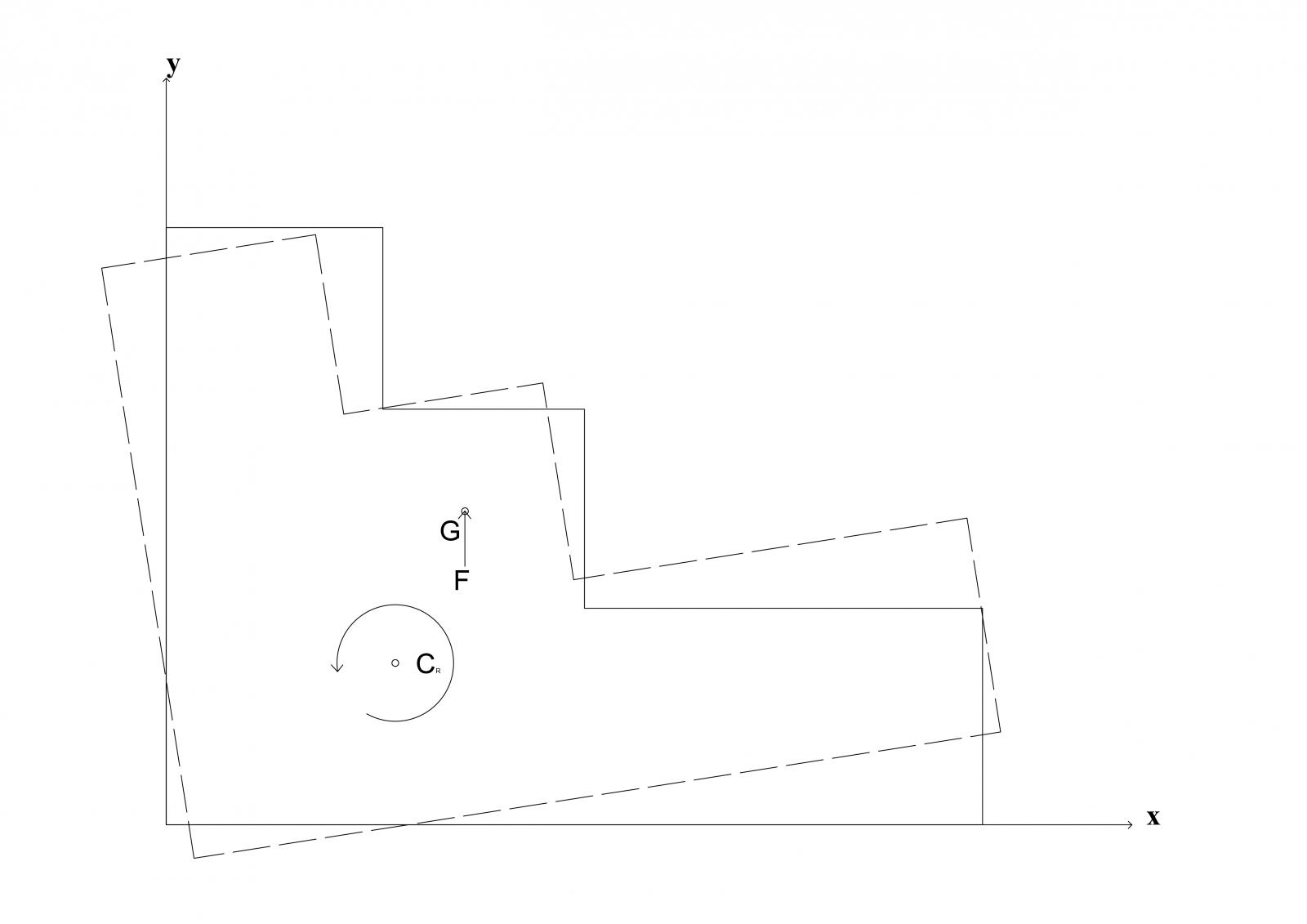Valuteremo le incognite cinematiche come segue:

Come possiamo vedere dalle tabelle le nostre previsioni erano corrette, ma possiamo vedere anche come i nostri controventi reagiscano bene, grazie alle loro rigidezze, offrendoci valori piuttosto contenuti di v, u e phi.