blog di pierluigi.ortolani

Per questa quarta esercitazione vogliamo vedere gli effetti di una forza orizzontale (nello specifico una forza sismica) su di un telaio piano, utilizzando il metodo delle rigidezze e applicnado la forza come F_x e F_y lungo le coordinate x e y .

Prendiamo in esame l'impalcato di un solaio appartenente ad un edificio monopiano,  di cui la struttura sia composta da telai piani realizzati in cemento armato. Questo telaio non soltanto permette di scaricare a terra i carichi mediante il flusso di carico verticale, ma anche di sopportare le azioni orizzontali ( che possono,ad esempio, essere causate da vento o sisma), funzionando come veri e propri controventi. Per prima cosa dobbiamo individuare i telai che compongono il nostro impalcato: avremo 4 telai paralleli alla direzione x  e 4 paralleli a y

1v- Pilastri: 1-5-9-12              1o- Pilastri: 1-2-3-4

2v- Pilastri: 2-6-10-13            2o- Pilastri: 5-6-7-8

3v- Pilastri: 3-7-11                 3o- Pilastri: 9-10-11

4v- Pilastri: 4-8                      4o- Pilastri: 12-13

Il controvento può essere definito come un appoggio cedevole elasticamente, in quanto corpo rigido sul proprio piano che si oppone elasticamente ad una forza orizzontale applicata.La capacità del controvento di opporsi (più o meno) a questa forza è la sua rigidezza. Per questo motivo possiamo vedere questi controventi come molle

Per questa esercitazione ipotizziamo che il telaio sia modellato come un telaio di tipo Shear-Type, la cui rigidezza traslante è:

Dobbiamo quindi tenere conto del modulo di elasticità E del materiale ( E c.a.= 21.000 MPa) e dei diversi Momenti di Inerzia legati alla forma della sezione del pilastro

• I_x= (bh³)/12=160.000 cm⁴
• I_y= 90.000 cm⁴

Nello STEP1, calcoliamo la rigidezza traslante associata a tutti i controventi, in base alle altezze H al modulo di elasticità E e ai momenti d'inerzia I, come già anticipato:

Nello STEP2 viene riportata una tabella riassuntiva dei valori delle rigidezze traslanti e delle distanze dei controventi da un polo O, origine di un sistema di riferimento cartesiano da me scelto.

Con lo STEP 3 intendiamo calcolare le coordinate del centro di massa dell'impalcato; per far questo lo suddividiamo in 3 Aree rettangolari i cui centri di massa relativi sono più immediati da individuare. Una volta noti questi, possiamo conoscere le coordinate x ed y di G grazie alla formula (derivata da quella per le coordinate del centro di un sistema di vettori paralleli:

Nello STEP 4 vengono calcolate le rigidezze totali sia verticale che orizzontale, nonché la rigidezza torsionale totale e il centro delle rigidezze come segue:

A questo punto possiamo applicare all'impalcato i centri di massa e rigidezza, confrontarne le posizioni relative e applicare una forza (sismica) orizzontale al centro di massa G per valutarne gli effetti cinematici.

Come è possibile immediatamente evincere dall'immagine soprastante, i due centri non coincidono, il che vuol dire che applicando forze in entrambe le direzioni la nostra struttura subirà non solo una traslazione ma anche una rotazione, provocata da un momento di intensità pari a F applicata in G per la distanza tra i due centri (braccio).

Nello STEP 5 analizziamo i carichi gravanti sulla struttura per conoscere l'effetto del carico sismico, tenendo presente che il solaio ipotizzato è in latero-cemento per un ufficio aperto al pubblico ( CAT-B2); l'analisi prevede:

dove: -G= carichi permanenti; - Q= carichi variabili; W= peso sismico; psi= fattore di contemporaneità; c= coeff. intesità sismica; F= forza sismica orizzontale

Infine, negli STEP 6 e 7 passiamo alla valutazione degli effetti cinematici della forza orizzontale, rispettivamente orientata lungo x e lungo y. Come già detto, prevediamo di avere sia traslazioni che rotazioni in entrambi i casi, in quanto i due centri C e G non combaciano.

-Effetti di forze orizzontali lungo x ed y:

Valuteremo le incognite cinematiche come segue:

Come possiamo vedere dalle tabelle le nostre previsioni erano corrette, ma possiamo vedere anche come i nostri controventi reagiscano bene, grazie alle loro rigidezze, offrendoci valori piuttosto contenuti di v, u e phi.

Per la terza esercitazione dimensioniamo la  mensola maggiormente sollecitata di un solaio generico, realizzato in acciaio, c.a. e legno.

1. Definizione dell'impalcato del solaio

Consideriamo un telaio 11.5 x 6 m, costituito da più campate, delle quali le ultime due siano sorrette da mensole; la mensola maggiormente sollecitata risulterà essere quella con l'area di influenza maggiore, di luce 2,5 m, interasse 3 m e area d'influenza 7,5 m² .

Oltre al dimensionamento delle tre mensole nelle tre tecnologie scelte, dovremo verificare per ognuna di esse l'abbassamento massimo verticale v_max e il rapporto tra la luce e l'abbassamento l/ v_max tale che I/v_max>250, ossia che l'abbassamento verticale non sia maggiore di 1/250 della luce in esame.

2. Dimensionamento delle tre mensole

Procederemo al dimensionamento delle mensole seguendo le modalità di procedimento del dimensionamento delle travi,discusso nell'esercitazione precedente:

• a. analisi dei carichi e calcolo di q_u
• b. calcolo del momento
• c. dimensionamento a flessione della trave

ricordandoci però che, data la geometria e la distribuzione delle forze della mensola,

il Mmax non risulterà uguale a quello di una trave doppiamente appoggiata; esso sarà dato dall'equazione:

                                                                     M_max= (q_u x l²)/2

2.a. ACCIAIO

Data la seguente stratigrafia, i carichi agenti ed il conseguente M_max risulteranno:

In questo caso, scelto un acciaio S235, avremo un profilato IPE 270, ottenuto sulla base del calcolo del modulo di resistenza a flessione W_x,min< W_d:

2.b. CALCESTRUZZO ARMATO

Per quanto riguarda il calcestruzzo armato, avremo carichi e Momento M_max come segue:

In base al momento, data una base di progetto b_d , dimensioniamo l'H_d e verifichiamo che l'aggiunta del peso proprio della trave al carico ultimo q_u non ne comprometta il dimensionamento iniziale:

In questo modo otterremo una sezione in c.a. 25x40 cm con acciaio B450C e cls C50/60

2.c. LEGNO

I carichi e il M_max agenti sulla trave lignea saranno:

e di conseguenza, tenendo conto della destinazione d'uso, della classe di servizio e del coefficiente di riduzione della resistenza k_mod, avremo una trave la cui sezione viene ingegnerizzata partendo dalla b_d di 30 cm:

Otteniamo così una sezione in GL24h 30 x 45 cm.

3. Calcolo e verifica degli abbassamenti per le tre mensole

Una volta dimensionate le tre mensole, come da precedente esercitazione, dobbiamo  calcolare e verificare per Normativa l'abbassamento verticale massimo della mensola; esso non deve superare 1/250 della luce ed è influenzato dalle caratteristiche geometriche e meccaniche del materiale, nonché dalla luce e dal carico agente sulla sezione, essendo dato da:

Poiché esso non compromette la capacità portante ultima della mensola, ma ne compromette comunque le prestazioni di esercizio, la combinazione di carico in analisi non è quella calcolata allo SLU q_u, bensì quella allo SLE per una combinazione di carico frequente q_e; esso è dato da:

         q_e= (q_s+ q_p+ psi₁₁ x q_a) x i

3.a ACCIAIO

• Calcolo di v_max:  noto il profilo IPE270 realizzato in acciaio S235, ne conosco anche il momento d'inerzia I_x e il modulo elastico E; posso pertanto calcolare il v_max= 0,14 cm come da formula ( tenendo conto del fatto che il peso della trave in acciaio viene sommato agli altri carichi nel calcolo di q_e)
• Verifica: l= 2,5 m, v_max= 0,14 cm l/v_max=1724,49>250    la verifica è soddisfatta

​

3.b. CALCESTRUZZO ARMATO

• Calcolo di v_max: determinata la sezione 25x40 e i due materiali costituenti, conosco il mod. elastico E e posso calcolare il momento d'inerzia I_x= (b x h³)/12; tenendo conto che anche per il c.a. il peso proprio della trave va sommato al carico, possiamo conoscere v_max= 0,46 cm
• Verifica: l=2,5 m, v_max=0,46 cm l/v_max= 536,72>250    la verifica è soddisfatta

3.c. LEGNO

• Calcolo di v_max: dimensionata la nostra sezione 30x45 cm in GL24h, ne conosco il modulo elastico e posso ricavare il mom. d'inerzia I_x= 227815,5 cm4 come visto in precedenza; ora possiamo conoscere l'abbassamento massimo v_max, sapendo che per il legno non si tiene conto del peso proprio della trave: v_max= 0,79 cm 
• Verifica: l=2,5 m, v_max=0,79 cm l/v_max= 316,06>250       la verifica è soddisfatta

Per la seconda esercitazione vogliamo dimensionare la trave principale  maggiormente sollecitata di un solaio generico, che venga realizzato in acciaio, c.a. e legno. 

1. Definizione dell'impalcato del telaio

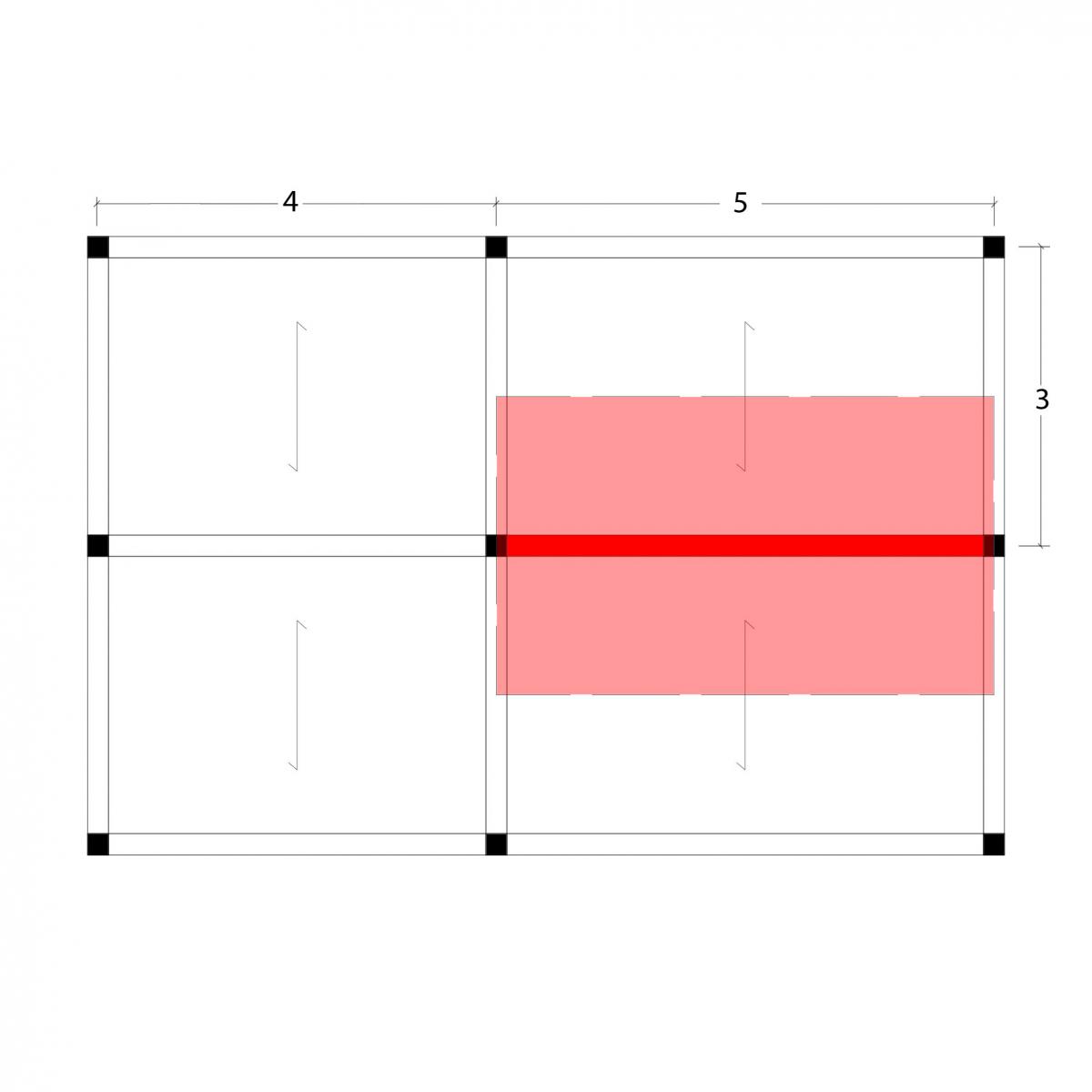
Ipotizziamo di considerare un telaio elementare 9x6m costituito da 4 campate; la trave maggiormente sollecitata risulterà essere quella con l'area d'influenza maggiore, di luce 5m, interasse 3, e area d'influenza 15 m². Questa sarà la trave che prenderemo in considerazione per le nostre tre tecnologie.

Poiché ogni tecnologia impiegata porta con sé una stratigrafia differente, avremo anche carichi e sollecitazioni agenti differenti. Consideriamo quindi i tre materiali separatamente.

2. Dimensionamento della trave in ACCIAIO

Immaginiamo un solaio in acciaio la cui stratigrafia comprenda un'orditura secondaria fatta da una lamiera grecata e da un getto di completamento in c.a., uno strato isolante e una pavimentazione in grès ceramico con strato di allettamento.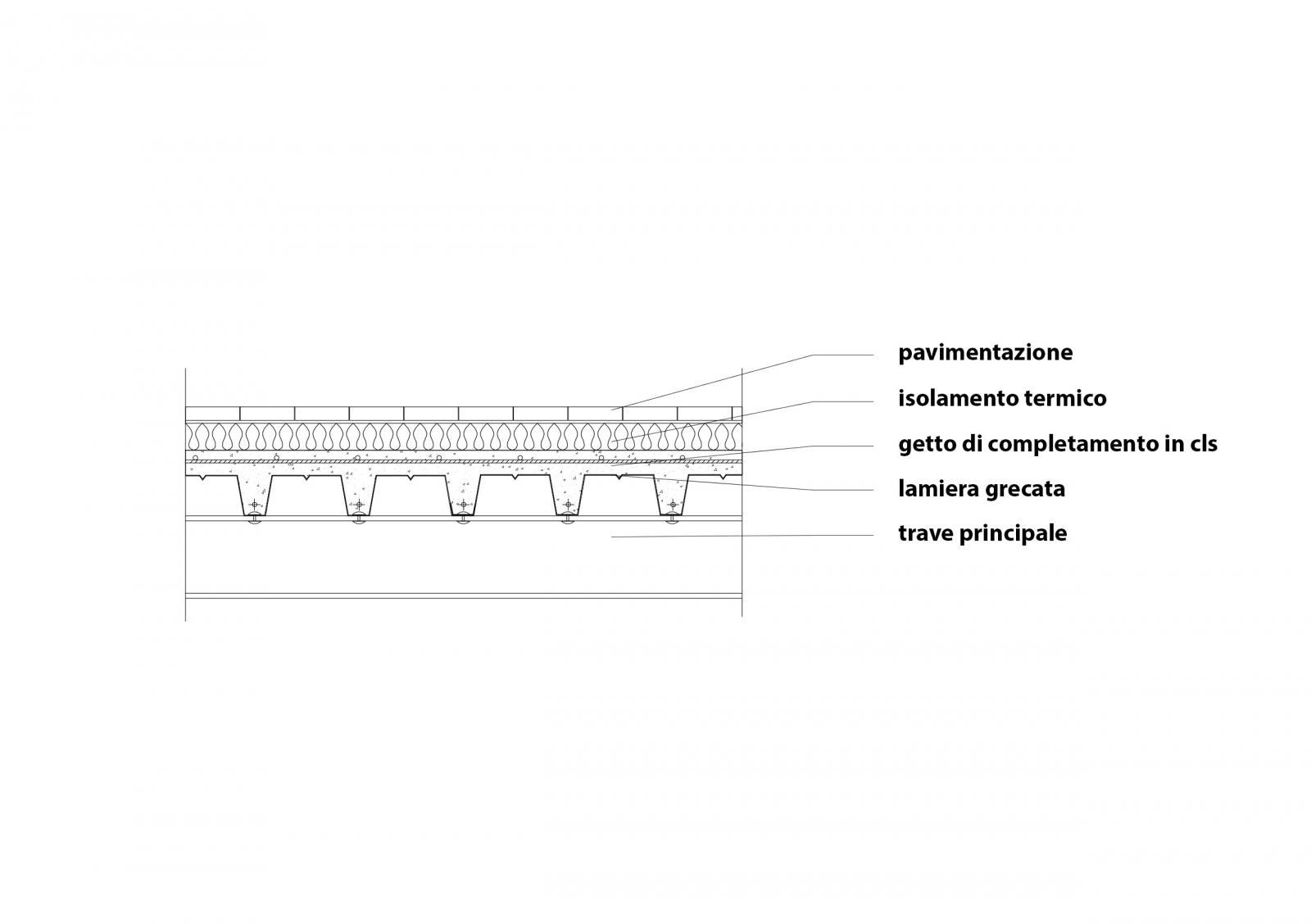

2.a. Analisi dei carichi

Per poter dimensionare la trave la prima cosa da fare è conoscere i carichi agenti su di essa; a tale scopo individuiamo carichi strutturali, permanenti e accidentali, sulla base degli elementi che compongono il solaio e della destinazione d'uso dell'edificio in questione. Un carico areale è il prodotto dello spessore per il peso per unità di volume gamma. La combinazione di carico allo SLU per il calcolo del carico lineare agente sulla trave, tiene conto dei carichi areali così definiti, dei coefficienti di sicurezza ad essi assegnati dalla norma e dall'interasse su cui essi agiscono:

                                                    q_u= i x (1,3 x q_s + 1,5 x q_p + 1,5 x q_a) [kN/m]

• q_s( kN/m²)= carichi strutturali:
  • lamiera grecata (sp. 10 mm x p.s.=10,47 kg/m³)= 0,1047 kN/m^2​
  •  getto cls (sp. medio (9,67+2,3)/2=5,98 cm x p.s.=25 kg/m³) = 1,5kN/m²
  • TOT.= 1,6 kN/m²
• q_p (kN/m²)= carichi permanenti:
  • pavimento in grès ceramico (sp. 0,02 m x0,2 kg/m³)= 0,4 kN/m²
  • isolante termico ( sp. 0,05 m)= 0,05 kN/m²
  • incidenza dei tramezzi= 1 kN/m²
  • incidenza degli impianti= 0,5 kN/m²
  • TOT.= 1,95 kN/m²
• ^​q_a (kN/m²)= carichi accidentali ( cfr. NT- D.M.14.01.2008)
  • cat. B2- Uffici aperti al pubblico= 3 kN/m²
• ^​q_u = 28,5 kN/m

2.b. Momento massimo

Trattandosi di una trave doppiamente appoggiata, il M_max  si troverà in mezzeria e sarà

                                     M_max= ql²/8

Nel caso in analisi avremo M_max= 89,06 kNm

2.c. Dimensionamento a flessione della trave

Per prima cosa scegliamo il tipo di acciaio che vogliamo utilizzare per la nostra trave, il che influenzerà le sue caratteristiche meccaniche e quindi geometriche. Ipotizziamo di utilizzare un acciaio S235 con tensione caratteristica di snervamento f_yk=235 MPa e una tensione di progetto f_yd= 223,8 MPa. Perché la trave resista a flessione dobbiamo trovare il modulo di resistenza a flessione minimo W_x,min tale che W_x,min<W_d per cui la trave resisterà alle sollecitazioni cui è sottoposta. A questo punto, basandoci sulle caratteristiche forniteci dai produttori che rispettano la normativa vigente, scegliamo un profilo adatto per la nostra trave. W_x,min può essere ricavato dalla seguente equazione:

                                 W_x,min= M_max/f_yd

Nel nostro caso W_x,min= 398 cm³; ne consegue che W_x,min<W_d=484 cm³ (profilo IPE 270)

3.Dimensionamento della trave in C.A.

Il secondo solaio ipotizzato viene realizzato con travi principali in c.a., un'orditura secondaria costituita da pignatte laterizie, una soletta di completamento e travetti di armatura in acciaio, e completato da uno strato isolante e da una pavimentazione in grès ceramico.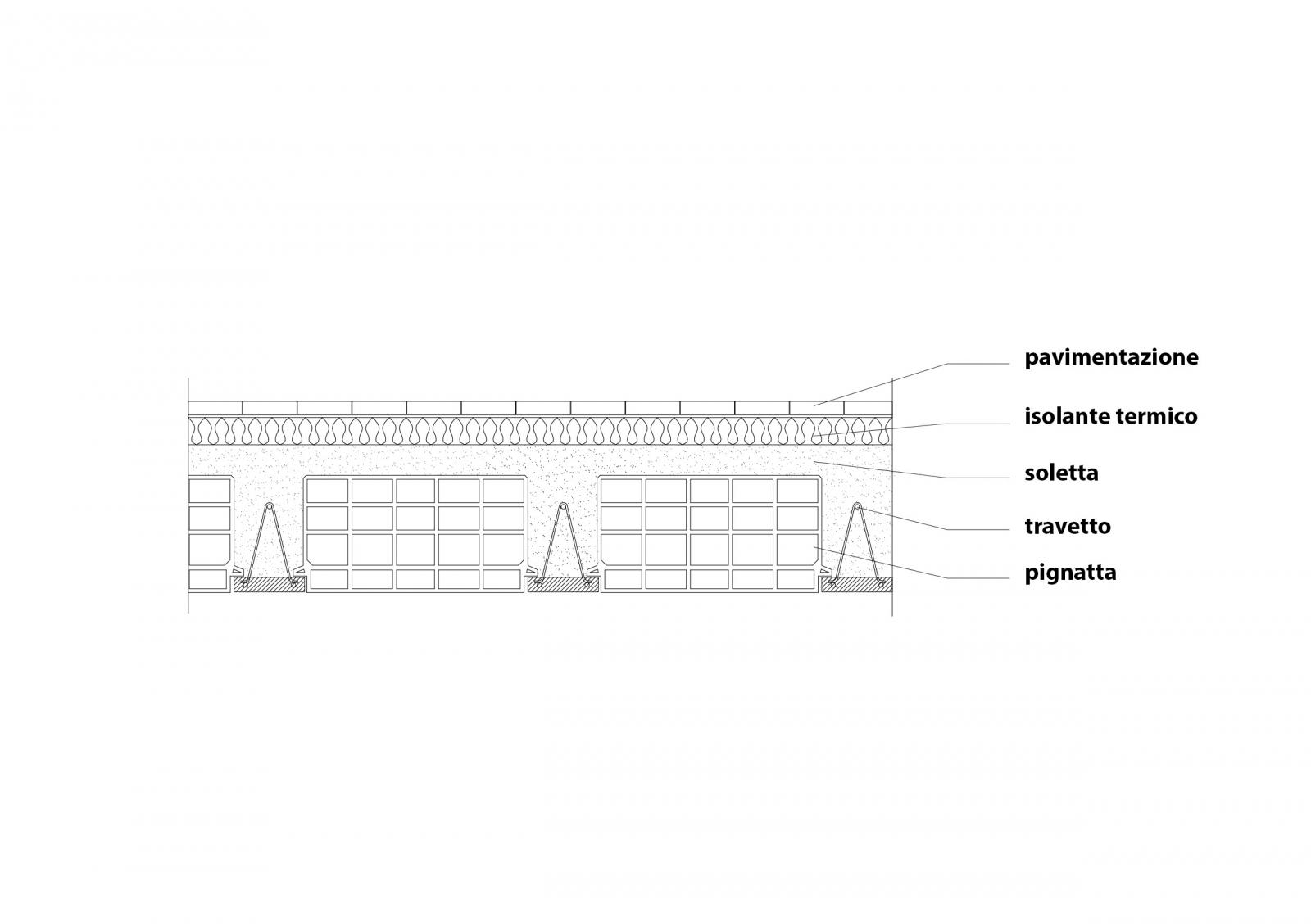

3.a. Analisi dei carichi

• q_s ( kN/m²)= carichi strutturali:
  • pignatta (38 cm x 0,2 cm x 6 kN/m³)= 0,92 kN/m²
  • soletta di completamento ( sp. 4 cm x 25 kN/ m³)= 1 kN/m² 
  • travetti in acciaio ( 12x20 cm)= 1,2 kN/m²
  • TOT.= 3,12  kN/m²
• ^​q_p (kN/m²)= carichi permanenti:
  • pavimento in grès ceramico (sp. 0,02 m x0,2 kg/m³)= 0,4 kN/m²
  • isolante termico ( sp. 0,05 m)= 0,05 kN/m²
  • incidenza dei tramezzi= 1 kN/m²
  • incidenza degli impianti= 0,5 kN/m²
  • TOT.= 1,95 kN/m²
• ^​​q_a (kN/m²)= carichi accidentali ( cfr. NT- D.M.14.01.2008)
  • cat. B2- Uffici aperti al pubblico= 3 kN/m^2​
• ^​q_u (kN/m)= 34,44 kN/m

3.b. Momento massimo

         M_max= 107,63 kNm

3.c. Dimensionamento a flessione della trave

Prima di tutto dobbiamo scegliere quali classi di materiali usare sia per l'acciaio che per il calcestruzzo. Definiti questi e fissata una base, possiamo trovare un H_min t.c. H_min<H_d, valore ingegnerizzato dell'altezza della sezione. Fatto ciò, a differenza del legno e dell'acciaio, il c.a. necessita di una verifica del peso proprio: essendo questo un dato rilevante dovremo verificare che l'aggiunta del peso della trave al carico q_u non comprometta la stabilità della trave appena dimensionata; dobbiamo cioè verificare che  anche la nuova H_min,2< H_d.

3.c.1. Materiali: 

• ACCIAIO B450C ( f_yd=391,3 MPa)
• CLS C50/60 ( f_cd=28,33 MPa)

3.c.2. Definizione di H_min: essa è il risultato della somma 

      H_min= h_u + d

  dove     - d (delta) = distanza tra l'asse dell'armatura inferiore e la fibra inferiore

               - h_u= distanza tra l'asse dell'armatura e la fibra superiore      

3.c.3. Definizione di H_d

Ponendo b_d= 25 cm  e d= 5 cm otteniamo H_min= 31,5 cm e H_d= 40 cm

3.c.4. Verifica di H_d

Una volta ingegnerizzata la sezione, verifichiamo infine il nuovo carico q_u, tenendo conto del peso della trave; perché sia soddisfatta la verifica dovremo avere che H_min,2< H_d.

4. Dimensionamento della trave in LEGNO 

L'ultimo solaio che prendiamo in considerazione è formato da un tavolato in legno d'abete con travetti secondari di quercia, un massetto e una pavimentazione in grès ceramico.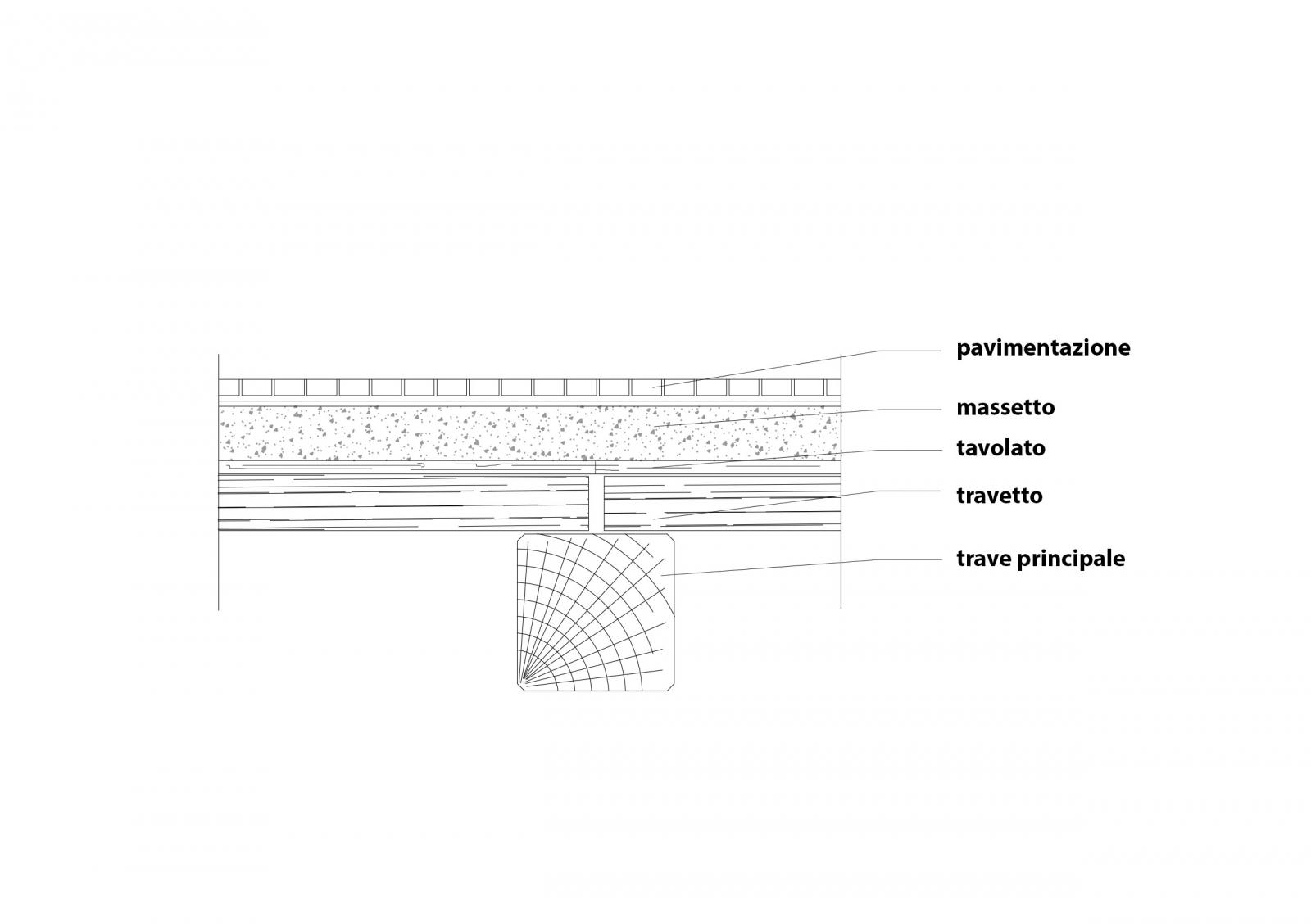

4.a. Analisi dei carichi:

• q_s (kN/m²)= carichi strutturali:
  • tavolato abete ( sp. 3 cm x 6 kN/m³)= 0,18 kN/m²
  • travetto secondario quercia ( sp. 8 cm x 8 kN/m³)= 0,64 kN/m²
  • TOT.= 0,82 kN/m²
• ^​q_p(kN/m²)= carichi permanenti:
  • pavimento in grès ceramico (sp. 0,02 m x0,2 kg/m³)= 0,4 kN/m²
  • massetto ( sp. 0,05 m x  19 kN/m³)= 0,95 kN/m²
  • incidenza dei tramezzi= 1 kN/m²
  • incidenza degli impianti= 0,5 kN/m²
  • TOT.= 2,85 kN/m²
• ^​​q_a (kN/m²)= carichi accidentali ( cfr. NT- D.M.14.01.2008)
  • cat. B2- Uffici aperti al pubblico= 3 kN/m^2​
• ​q_u (kN/m)= 29,52 kN/m

4.b. Momento massimo:

          M_max= 92,25 kNm

4.c. Dimensionamento a flessione della trave:

Per poter dimensionare la trave in legno devo decidere a priori il tipo di legno impiegato, perché le caratteristiche meccaniche cambiano in funzione della classe del legno prescelto. Avendo deciso di utilizzare un legno lamellare, ci rifacciamo alla normativa UNI EN 1194 per scegliere la classe da impiegare:

prendiamo per esempio il GL24h, che ha una resistenza caratteristica a flessione f_m,k= 24 MPa.

A questo punto per conoscere la resistenza di progetto fd, dobbiamo tener conto dei coefficienti k_mod ( coeff. diminutivo del valore di resistenza del materiale) e g_m ( coeff.parziale di sicurezza), poiché

                                                f_d= k_mod x (f_m,k/ g_m)

dove            - k_mod=0,6 dipende dalla classe di durata del carico( durata permanente) e dalla                       classe di servizio ( classe 1)

                   - g_m= 1,45  ( per legno lamellare incollato)

Ne consegue che f_d= 9,93 MPa.

Ora, fissata b_d= 30 cm, possiamo calcolare h_min e quindi H_d t.c. h_min<H_d

h_min= {[(6 x M_max) / (f_d x b)]}^0,5= 43,1 cm < H_d=45 cm

Per la prima esercitazione dimensioniamo una trave reticolare a nostra scelta. Io ho pensato ad una travatura costituita da profili in acciaio a sezione circolare cava con  una maglia di 4x4 moduli piramidali ( dimensioni: 8x8x2 m).

1. Creare un nuovo modello

Per prima cosa ho bisogno di creare un nuovo modello per poter lavorare: quindi seleziono File> New Model> Select Template> Grid Only, facendo attenzione a scegliere le unità di misure corrette [ kN, m, C]; a questo punto posso inserire i dati che mi servono per costruire la mia griglia e il mio modulo di base:

Una volta creato il modulo iniziale, lo copio per formare la mia struttura reticolare 4x4; nel copiare faccio attenzione a non sovrapporre frame nelle direzioni x,y perché porterebbero a errori nel calcolo della struttura. Una volta ultimata, la mia struttura si presenta così:

2. Carichi e vincoli

A questo punto carichiamo la struttura attraverso una serie di forze concentrate nei nodi strutturali: forze di entità maggiore nei nodi centrali ( 100 kN), e minore in quelli perimetrali ( 50 kN); questo perché le aree di influenza dei nodi laterali sono la metà di quelli centrali, ciò significa che saranno sottoposti a forze più piccole. Per aggiungere delle forze seleziono le frame che mi interessano e poi Assign>Joint Loads> Forces, da questa finestra di dialogo posso creare nuove forze con intensità e direzione variabile: io creo forze f con direzione Z di intensità -100 o -50, perché rivolte verso il basso.

In seguito, assegno i vincoli cerniera sul piano xy ( per visualizzarlo: View> Set 2D View) selezionando i Grid Point che mi interessano e Assign>Joints>Restraints>Fast Restraints>Cerniera . Perché i nodi tra le aste vengano considerati dal programma tutte delle cerniere, dobbiamo poi effettuare il rilascio dei momenti: per questo seleziono tutti i frame e Assign>Frame>Release/Partial fixity> Release e spunto Start e End dei due Momenti flettenti che si generano nei due piani, l'uno minore l'altro maggiore. In questo modo in ogni nodo il momento sarà pari a 0. Per completare questa fase, assegno a tutti i frame una sezione circolare cava selezionando Assign>Frame>Frame Sections>Add new Property e creando  una sezione con le caratteristiche geometriche e i materiali che preferisco.

3. Analisi

Ora posso far analizzare al programma la mia struttura. Essendo una travatura reticolare con forze concentrate sui nodi mi aspetto che essa sia sottoposta a soli sforzi assiali N, senza quindi che si producano T (Shear) o M ( Moment). Per far partire l'analisi seleziono Run> Select Load Cases to Run e spunto solo le forze f; una volta salvato il file, SAP mi restituisce l'analisi del modello: da qui, posso verificare che la mia ipotesi di soli sforzi assiali sia corretta, oppure posso visualizzare la deformata della struttura.

Arrivati a questo punto, per poter lavorare con i dati fornitimi dal programma su Excel, ho bisogno delle Tabelle: quindi con CTRL+T ottengo delle tabelle su diverse caratteristiche della struttura; a me interessa la tabella Element Forces-Frames, da cui deduco il numero e il nome delle aste e le loro caratteristiche di sollecitazione.

A questo punto posso importare i dati su Excel, e procedere col dimensionamento delle sezioni.

4.Dimensionamento delle Aste Tese

Una volta che i dati relativi alle aste sono stati suddivisi tra aste tese e aste compresse, posso passare a riorganizzare quelli riguardanti le aste sottoposte a trazione e quindi procedere col dimensionamento delle sezioni.

Prima di tutto eliminiamo i doppioni che alle varie Station SAP ha calcolato, poi le riordiniamo dal più piccolo al più grande. Per progettare un'asta soggetta a trazione dobbiamo ricavare l'A_min, che ci assicura la resistenza della sezione a trazione. Una volta ottenuto, questo valore va ingegnerizzato, cioè confrontato con la tabella dei profili a sezione cava (da noi scelti per queste aste), per trovare l'area immediatamente più grande che soddisfi le nostre esigenze, di modo che A_d> A_min. La formula di progetto per le aste tese è

A_min= N/f_yd 

Dai calcoli così eseguiti, troviamo che per le 71 aste tese avremo bisogno di soli due profili diversi: 4 profilati 33,7x3,2 e 67 profilati 33,7x2,6.

5. Dimensionamento delle Aste Compresse

Le aste compresse, oltre a tener conto dell'A_min per la resistenza della sezione, sono soggette anche a instabilità, che dipende dalla luce e dalla snellezza dell'elemento che andiamo a dimensionare; per questo motivo dobbiamo tener conto dell'Inerzia e del raggio di inerzia offerti dalle sezioni; dobbiamo quindi verificare che A_min<A_d, I_min<I_d, rho_min<rho_d e che per Normativa lam<200. Eseguiti questi calcoli,dal confronto con le tabelle dei Profilati metallici ottengo 11 profili 76,1x3,6, 12 profili 60,3x2,9, 6 profili 60,3x3,6, 8 profili 48,3x2,6, 4 profili 42,4x3,2, 18 profili 42,4x2,6, 6 profili 33,7x2,9 e 22 profili 33,7x2,6.

Infine, per semplificare, raggruppo alcuni profilati insieme, sulla base delle caratteristiche geometriche ( sempre tenendo conto che per due sezioni diverse con momenti d'inerzia e aree maggiori/minori, devo dimensionarle prendendo in esame il caso più svantaggioso, cioè la sezione più sollecitata). Avrò quindi le mie 87 aste compresse così dimensionate:

• 11 profili 76,1x3,6
• 18 profili 60,3x3,6
• 8 profili 48,3x2,6
• 22 profili 42,4x3,2
• 28 profili 33,7x2,9