ESERCITAZIONE 4: Ripartizione delle forze sismiche

Con questa esercitazione vedremo come una forza orizzontale (ad esempio vento o sisma) si ripartiasce su un edificio, per eseguire questa analisi utilizzeremo il metodo delle rigidezze per vedere le reazioni del nostro impalcato.

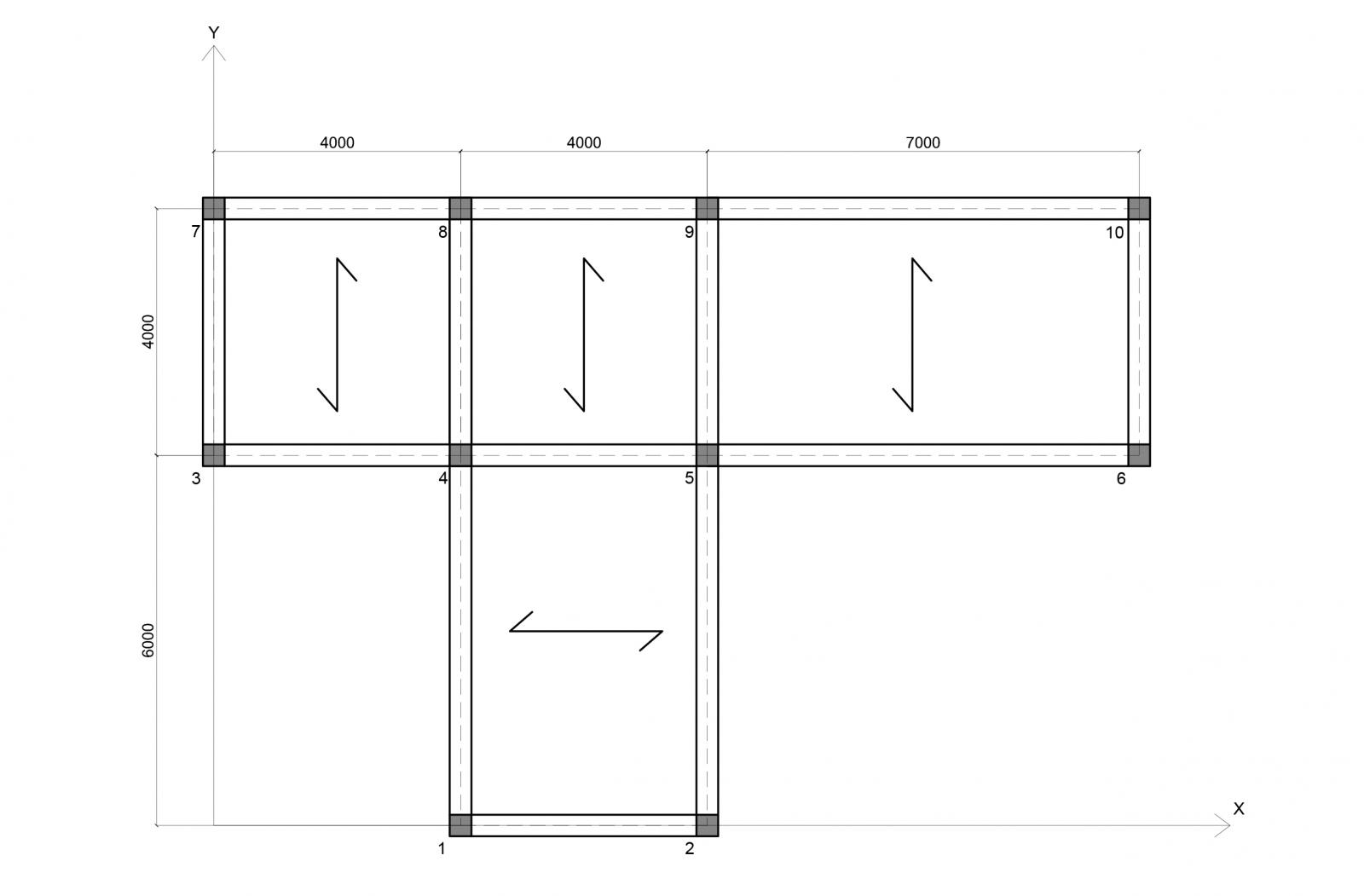
L'oggetto in analisi è un edificio ad un piano con una struttura i cemento armato composta da 7 telai (3 orizzontali e 4 verticali)

Telai orizzontali    

Telaio 1o: 1-2

Telaio 2o: 3-4-5-6

Telaio 3o: 7-8-9-10

Telai vertical

Telaio 1v: 3-7

Telaio 2v: 1-4-8

Telaio 3v: 2-5-9

Telaio 4v: 6-10

Di questi telai analizzeremo le rigidezze considerandoli come modelli shear-type, un modello teorico che descrive un telaio con tutti nodi ad incastro e travi infinitamente rigide a flessione, questo ci permette di concentrarci solo sul cedimento vincolare dei pilastri (i controventi della struttura) e quindi sulla loro rigidezza.

Vediamo che la rigidezza dei telai dunque è direttamente proporzionale al modulo di Young E, al momento di inerzia I e inversamente proporzionale all'altezza h del pilastro. Per conoscere la rigidezza del nostro telaio basterà dunque sommare le rigidezze dei singoli controventi disposti sul rispettivo asse in analisi

kᵢ=12EI₁/hᶟ

k_tot=∑ᶰᵢ‗₁ kᵢ

Detto ciò visualizzo l'impalcato come un corpo rigido dotato di massa omogenea, controventato da vincoli cedevoli elasticamente rappresentabili sul piano xy come molle di adeguata rigidezza k

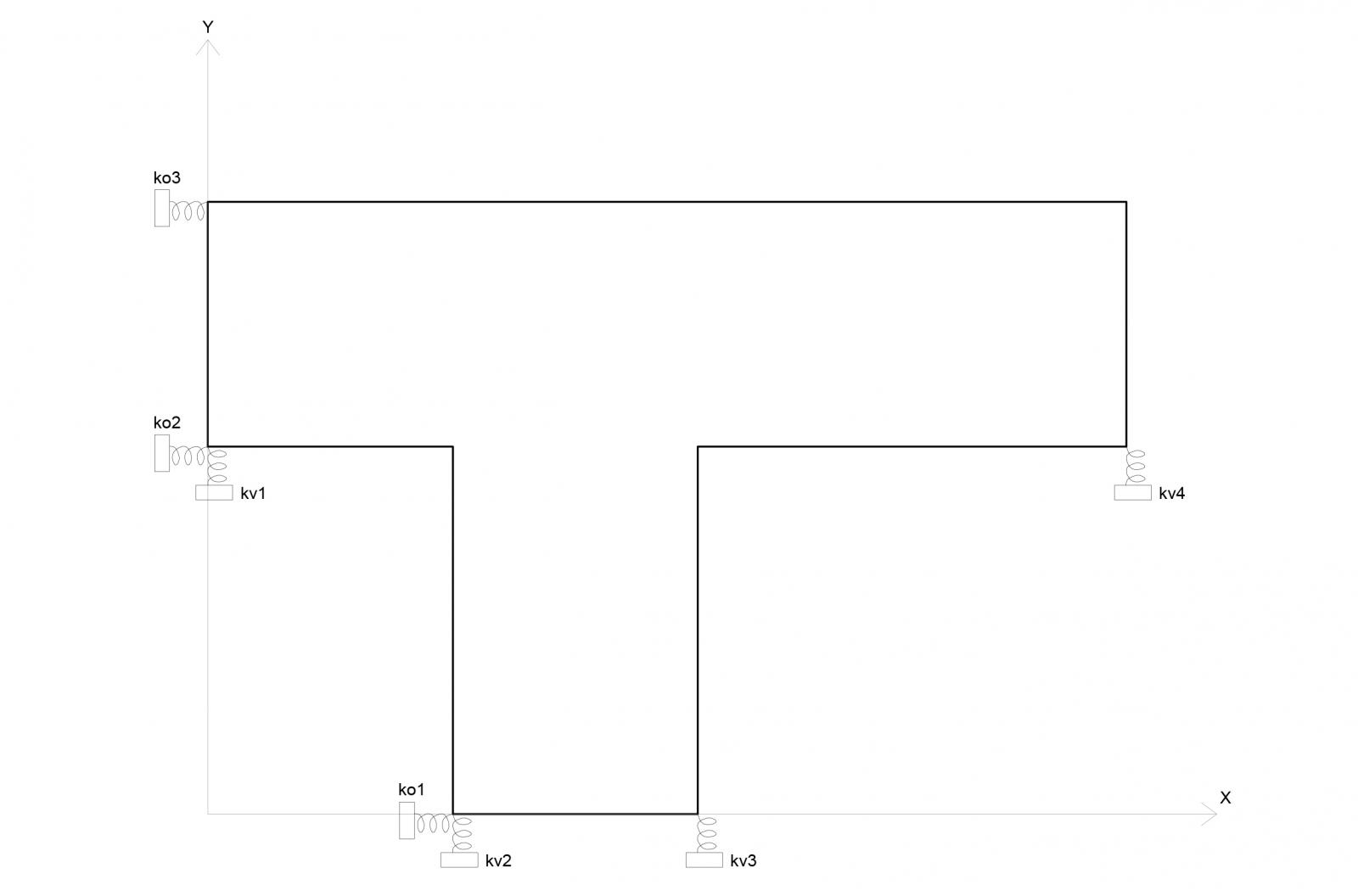
Prima di utilizzare il foglio excell per calcolare sistematicamente le rigidezze dei telai definisco che:

H= altezza = 3,4 m

E= Modulo di Young = 21000 N/mm²

Pilastri a sezione quadrata 30cmx30cm con un momento di inerzia unico

I= Momento d’Inerzia = b⁴/12 = 67 500 cm⁴

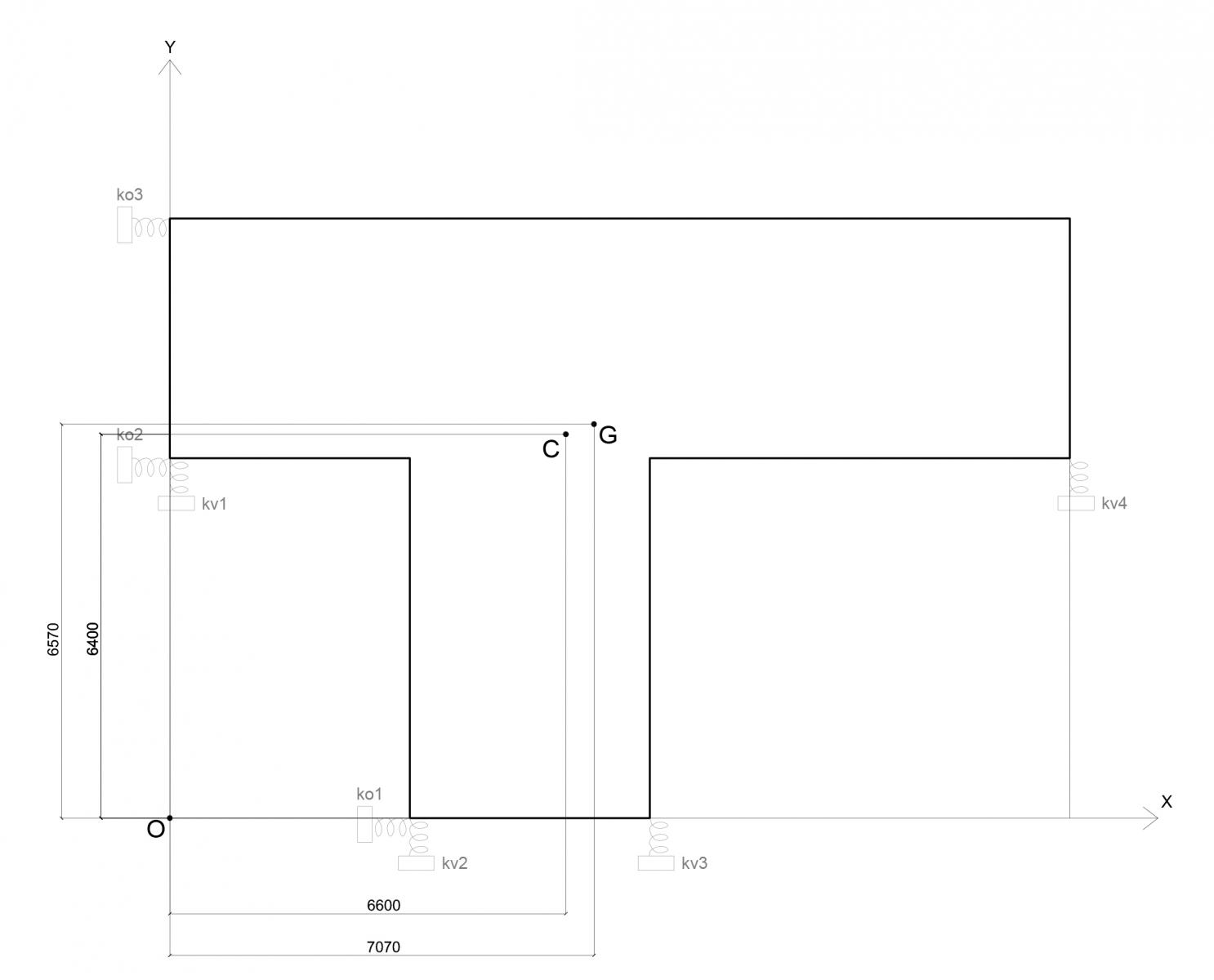
Una volta ricavate le rigidezze dei diversi telai riportiamo le distanze degli stessi da un punto d' origine (da noi scelto) chiamato O.

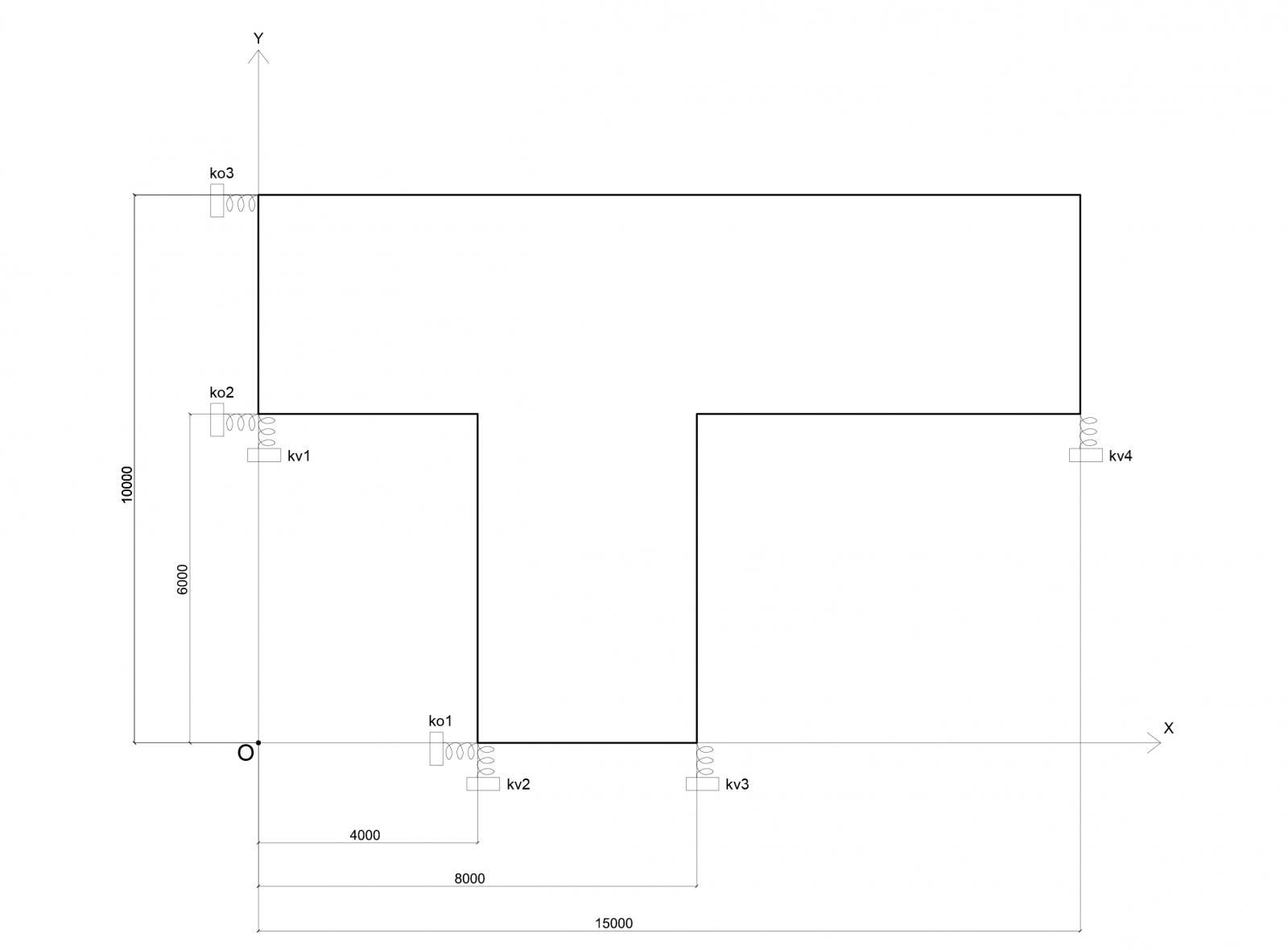
Una volta impostato questo sistema di riferimento passiamo a calcolare il centro di massa e il centro di rigidezza della struttura. Questi due punti possono essere entrambi ricavati utilizzando l'equazione per ottenere il centro di un sistema di vettori paralleli.

Per quanto riguarda il centro di massa esso coinciderà con il centro dell'area poichè abbiamo impotizzato che la densità della massa sia uniforme su tutto l'impalcato. per ricavarlo scomponiamo il corpo del nostro edificio in due figure geometriche distinte.

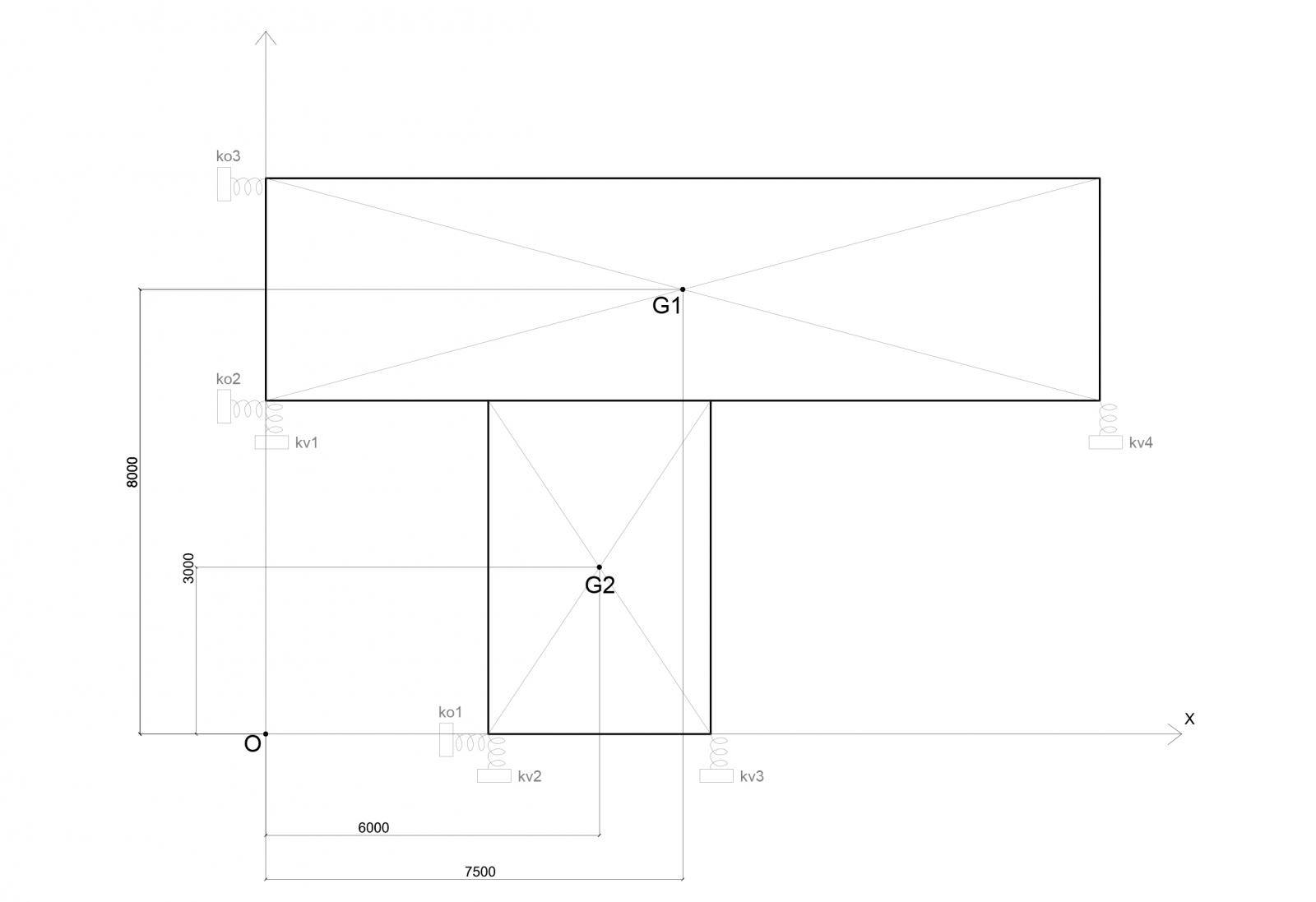
G1: x1= 7,5m

       y1= 8m

G2: x2= 6m

       y2= 3m

Dunque  

x_G = (Σ_i=1-nAixXGi)/ A_tot  

y_G = (Σ_i=1-nAixyGi)/ A_tot       

Per calcolare il centro delle rigidezze utilizzeremo (come introdotto precedentemente) la medesima equazione:

x_C = (Σ_i=1-nKvi x Dvi) / K_{v_tot}

y_C = (Σ_i=1-nKoi x Doi) / K_{o_tot}

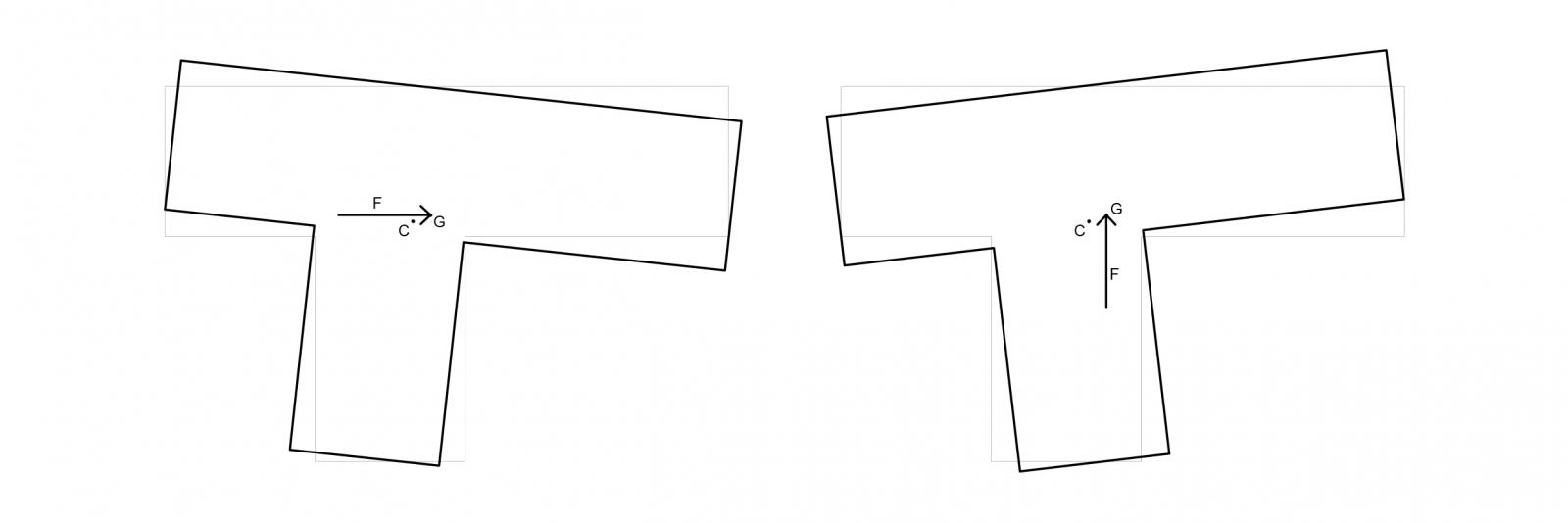
Trovati i due centri noto che non coincidono, questo significa che il nostro impalcato sarà soggetto, oltre che a traslanzione, anche a rotazione, questo perchè la forza orizzontale applicata al centro della massa farà ruotare l'impalcato con perno nel centro delle rigidezze, creando un momento con braccio pari alla distanza dei due centri, questo ci dice che la configurazione ottimale per una struttura è quella in cui coincidono i due centri.

Dunque bisogna calcolare anche il valore della rigidezza torsionale K_Φ che non è altro che la sommatoria delle rigidezze dei telai moltiplicati per la rispettiva distanza (braccio) dal centro delle rigidezze

K_Φ =Σ_i=1->nK_vi x dd²_vi  +  K_o x dd²_oi

Seguendo la normativa è possibile ricavare (approssimativamente) la forza sismica che potrebbe agire sul nostro edificio. Per fare questo ho bisogno di ricavarmi la forza peso dell'edificio W, dato dalla somma del carico permanente G e del carico accidentale Q moltiplicato per un coefficente di contemporaneità  ψ,  nel nostro caso ipotizzando un ambiente ad uso commerciale il nostro edificio apparterrà alla categoria D con un coefficente ψ = 0,6

W = G + Q x ψ

La forza peso dell'edificio infine dovrà essere calcolata per un coefficente di intensità sismica c che dipende dal luogo del progetto.

F= W x c

Ricavata la forza passo a verificare la sua influenza sulla nostra struttura nei versi dei controventi da noi analizzati.

Dove :

lo spostamento orizzontale         u= F/ko_tot

Lo spostamento verticale            v= F/kv_tot

La rotazione                                     φ=M/kφ

Determinati i valori dei gradi di libertà è possibile concludere ricavando la forza sui singoli controventi nei due casi di carico.

Forza sismicalungo l’asse x

reazione controventi orizontali     F_{o_n}= k_{o_n} (u+Φ x dd_{o_n})

reazione controventi verticali        F_{v_n}=k_{v_n} x Φ x dd_{v_n}

Forza sismicalungo l’asse y

reazione controventi orizontali     F_{o_n}=k_{o_n} x Φ x dd_{o_n}

reazione controventi verticali        F_{v_n}=k_{v_n}(v+ Φ x dd_{v_n})