Esercitazione 1 - Crisciotti, Latour, Zampilli

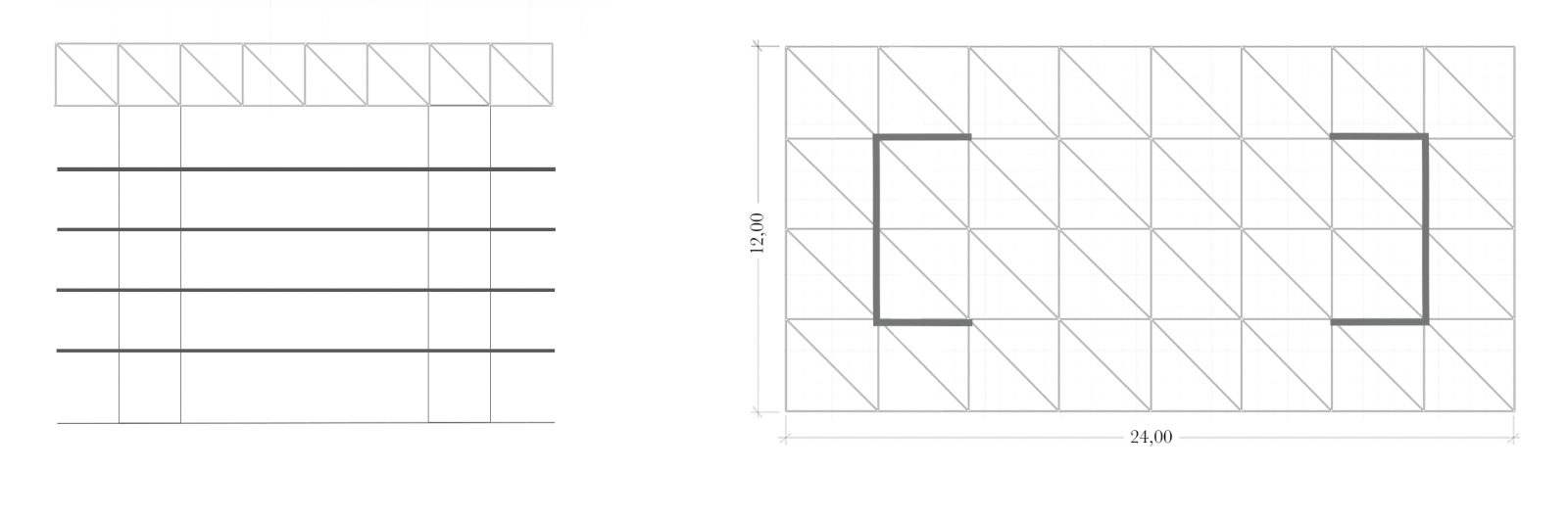
Ai fini dell’esercitazione abbiamo ipotizzato un edificio con una copertura reticolare alla quale sono stati appesi quattro piani sottostanti. La copertura, di dimensioni 24,00 m x 12,00 m x 3,00 m, è appoggiata su due vani scala costituiti da setti murari in calcestruzzo armato.

Dopo aver disegnato la reticolare su SAP2000 siamo andate a definire e assegnare alla struttura il materiale scelto per i profili delle aste, nel nostro caso l'acciaio S275. Abbiamo poi definito e assegnato alle aste una sezione provvisoria di tubo in acciaio a sezione circolare dal profilario integrato di SAP: andremo successivamente a dimensionare correttamente le sezioni dopo aver calcolato il valore degli sforzi su ogni asta. 
Siamo andate quindi ad assegnare i vincoli, sia le cerniere esterne in corrispondenza degli appoggi della struttura, sia le cerniere esterne impostando il rilascio dei momenti all'inizio e alla fine di ogni asta.

Andiamo quindi a definire i carichi da assegnare ai nodi della struttura, senza considerarne il peso proprio. Innanzitutto abbiamo calcolato le azioni agenti sulla struttura distinguendole in base alla loro intensità nel tempo.

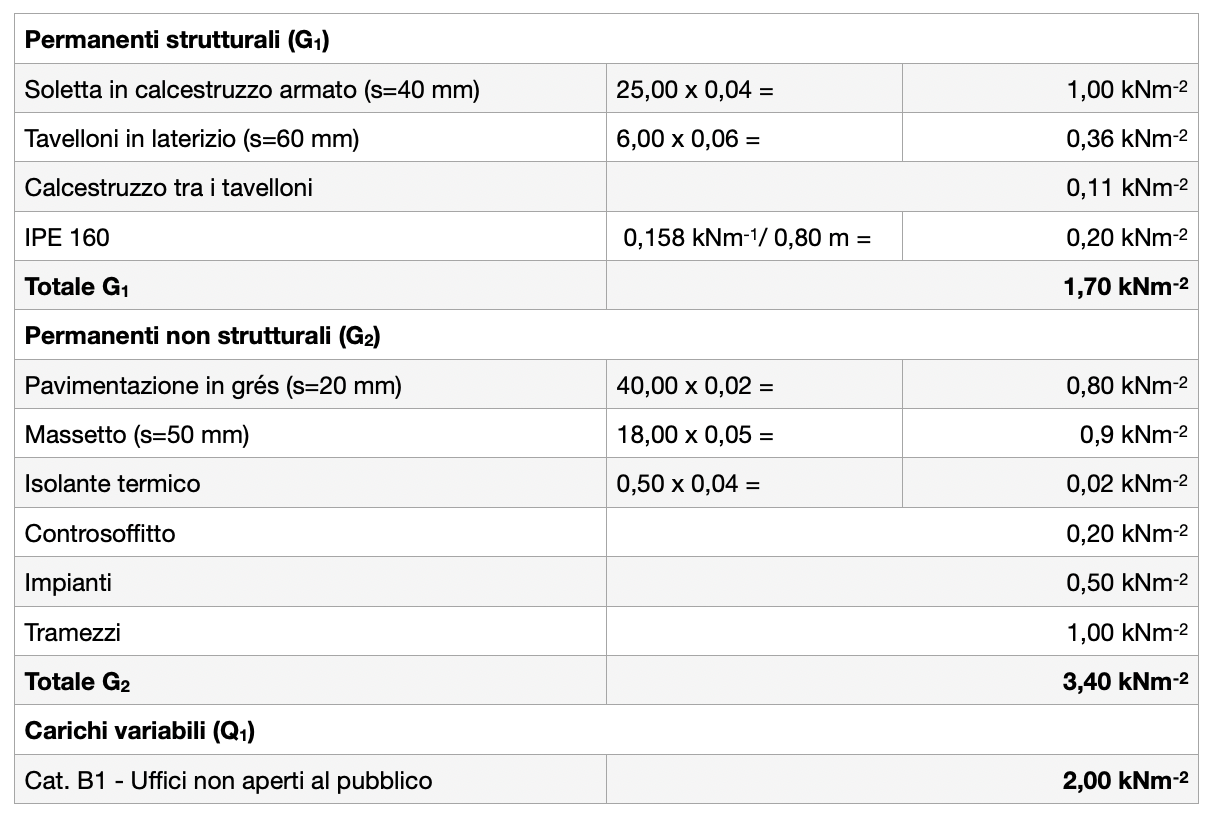
 Si è poi tenuta in considerazione la combinazione fondamentale di carico usata per le verifiche allo SLU con coefficienti parziali di sicurezza sfavorevoli. 
Il peso totale risulta quindi: q_u= γ_G1 x G₁ + γ_G2 x G₂ + γ_Q2 x Q₁= 1,3 x 1,70 + 1,5 x 3,40 + 1,5 x 2,00 =10,30 kNm^-2
Andiamo a calcolare il carico ripartito su ogni nodo in base alla sua area di influenza e alla sua posizione in pianta. Su ciascun pilastro gravano i carichi disposti nella sua area di influenza quindi in definitiva sui pilastri agirà una forza pari a:

Assegniamo quindi su SAP2000 le forze puntiformi che agiscono sui nodi della struttura. 
Facciamo partire l'analisi: otteniamo la conformazione deformata e i valori delle sollecitazioni e degli abbassamenti.

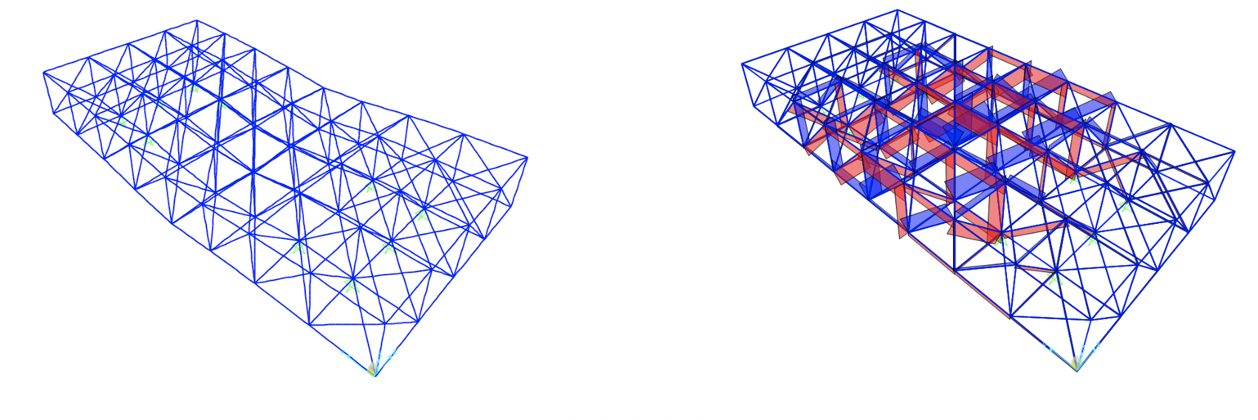
Esportiamo le tabelle delle sollecitazioni e andiamo ad individuare le aste maggiormente soggette a compressione e a trazione.

Andiamo quindi a dimensionare le aste soggette a trazione: calcoliamo l’area minima del profilo data dal rapporto tra lo sforzo normale agente sull’asta e la resistenza di calcolo dell’acciaio S275.
A_min = N*fyk/γ_m
Dopo aver scelto il profilario di riferimento cerchiamo un profilo che abbia un’area leggermente maggiore dell’area minima calcolata. Per comodità abbiamo suddiviso le aste tese in 6 gruppi in base alla sollecitazione agente.

Dimensioniamo ora le aste soggette a compressione allo stesso modo di quelle a trazione. Dobbiamo però verificare che le aste non subiscano fenomeni di instabilità a carico di punta. Andiamo quindi a calcolare il raggio di inerzia minimo della sezione e la snellezza critica della sezione, ovvero la snellezza limite superata la quale l’asta va in instabilità.
λ = π  √ (E / fyd)
ρ_min = β*l / λ
I_min = A_min*(ρ_min)²
Andiamo quindi a cercare sul profilario una sezione che abbia non solo area leggermente superiore a quella minima ma anche un raggio di inerzia maggiore di quello minimo calcolato. Come per le aste tese abbiamo individuato 6 profili differenti per le aste compresse. 

Andiamo ad assegnare su SAP alle aste le sezioni correttamente dimensionate: per comodità assegniamo a tutte le aste una sezione tubolare che ha come area una media delle sezioni dimensionate con gli sforzi ottenuti dall’analisi del modello. 

A questo punto calcoliamo il peso proprio della struttura: su SAP facciamo un’analisi con il solo carico DEAD che ha come Self Weight Multiplier 1 e si comporta dunque come carico uniformemente distribuito. Tramite i valori delle reazioni vincolari in corrispondenza delle cerniere esterne riusciamo ad ottenere un valore molto vicino a quello reale del peso proprio. Esportando la tabella delle reazioni vincolari e sommando i valori di quelle verticali otteniamo quindi il peso proprio della struttura. 

Con il valore ottenuto andiamo a definire un nuovo caso di carico, PP, con moltiplicatore 0 perchè andremo ad assegnarlo come carico concentrato. Andiamo ad applicare i carichi sui nodi: dopo aver diviso il valore totale del peso proprio per il numero di nodi applichiamo questo carico ai nodi centrali, ai nodi laterali la metà del carico applicato sui nodi centrali e agli angolari 1/4 del carico applicato sui nodi centrali.

Creiamo una nuova combinazione di carico data dalla somma del peso proprio della struttura e il carico allo SLU: facendo partire l’analisi ed esportando le tabelle delle sollecitazioni con questa combinazione di carico dovremmo avere un risultato non molto differente da quello ottenuto con il solo carico allo SLU poiché l’influenza del peso proprio sulle strutture in acciaio non è particolarmente rilevante. 

Di contro, però, le strutture in acciaio sono caratterizzate da elevata deformabilità se sottoposte a carichi ed è quindi necessario effettuare verifiche di deformabilità in condizioni di esercizio. 
Calcoliamo quindi la combinazione fondamentale di carico allo SLE che ha coefficienti di sicurezza più bassi rispetto allo SLU:
q_e= γ_G1 x G₁ + γ_G2 x G₂ + γ_Q2 x Q₁= 1,00 x 1,70 + 0,7 x 3,40 + 0,7 x 2,00 = 5,50 kNm^-2
Il carico totale allo SLE risulta quindi: 5,50 kNm^-2 x 288 m^-2x 4 piani = 6336 kN
Come abbiamo fatto in precedenza assegniamo il carico allo SLE ai nodi e facciamo un’analisi delle sollecitazioni agenti sulla struttura nel caso di una combinazione di carico PP+ q_e. 
Esportiamo quindi la tabella che mostra lo spostamento dei nodi rispetto alla posizione iniziale: per normativa gli spostamenti verticali per le coperture devono essere inferiori a L/200 dove L è la luce maggiore tra l'appoggio e il nodo. 

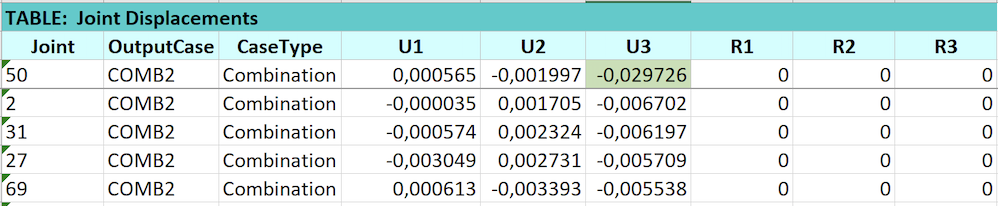
Verifichiamo che 0,0297 m sia inferiore a L/200, con L pari a 18 m. Nel nostro caso la verifica di abbassamento è soddisfatta dato che 0,0297 m < 0,09 m.