blog di Vittoria Latour

L’esercitazione prevede il dimensionamento e la verifica di un graticcio costituito da travi inflesse incastrate in ogni nodo. 
Ipotizziamo un telaio di 30x30 m con 5 piani fuori terra, sorretto da pilastri posti ad un interasse di 10 m. Ipotizziamo una sezione dei pilastri di primo tentativo, distinguendo tra pilastri angolari e pilastri perimetrali con un calcestruzzo di classe di resistenza C50/60.

Cominciamo a modellare la struttura su Sap assicurandoci che i pilastri siano posti di coltello, quindi con l’inerzia maggiore nella direzione di sviluppo del graticcio.
Anziché modellare direttamente il graticcio ne simuliamo il comportamento attraverso l’uso di un modello continuo equivalente, una piastra discretizzata, per valutare le sollecitazioni agenti sulla struttura: con queste dimensioneremo i pilastri e le travi del graticcio. Scegliamo uno spessore iniziale della piastra di 1 m e un calcestruzzo C50/60 con coefficiente di Poisson pari a 0 per tenere conto della formazione di vuoti dovuta alla deformazione. Assegniamo poi ai pilastri le sezioni e i vincoli esterni. Applichiamo le forze agenti sulla struttura come carichi puntiformi considerando il carico allo SLU utilizzato nelle altre esercitazioni, pari a 10,31 kNm^-2, differenziando la forza agente sui nodi angolari, perimetrali e centrali in base all’area di influenza. 

A questo punto facciamo partire l’analisi con il carico applicato e il peso proprio degli elementi strutturali per ricavare il momento massimo agente sulla struttura con cui dimensionare le travi del graticcio e i pilastri. 
Visualizziamo la deformata e i valori del momento sulla piastra. 

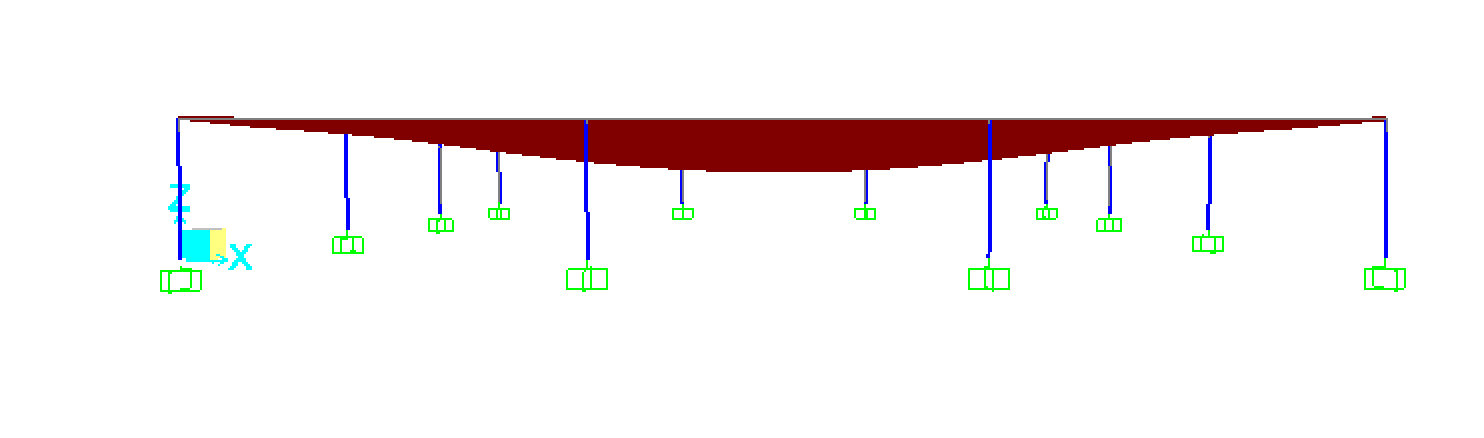
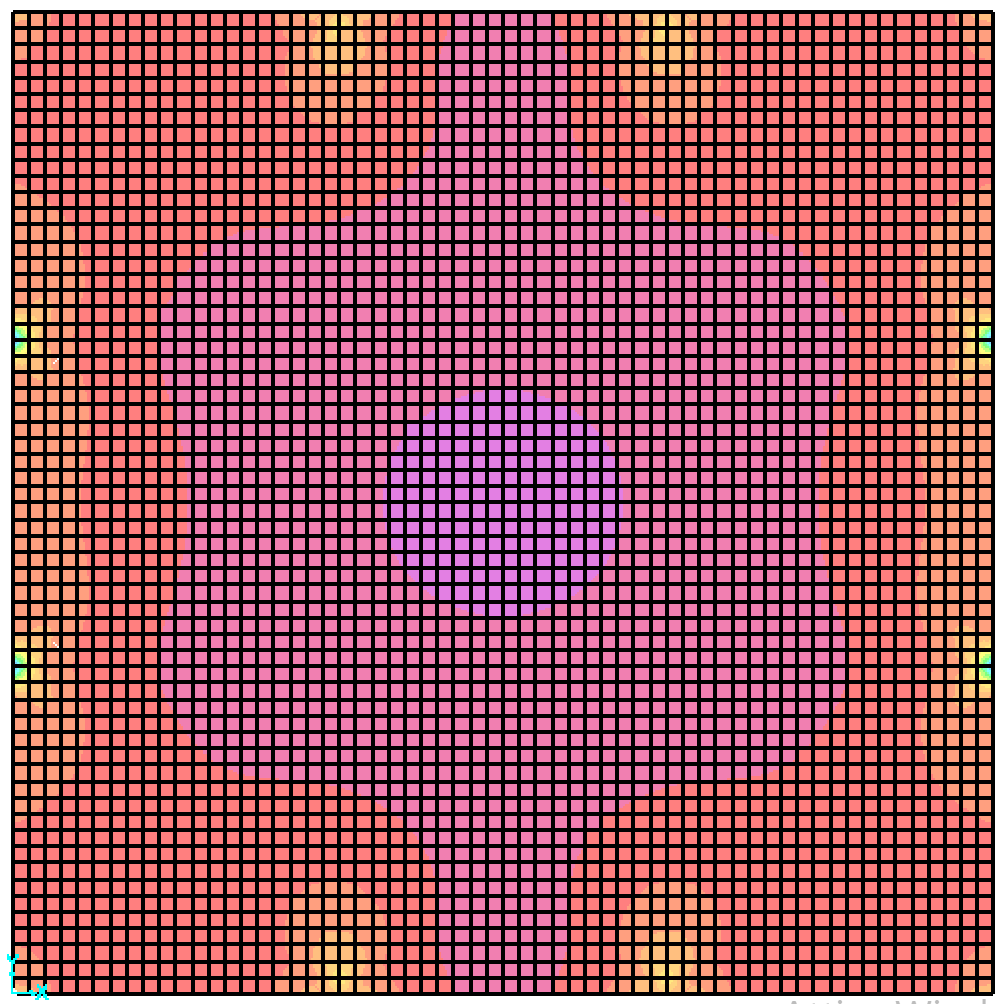
Prima analisi
Pilastri angolari                     1x1m
Pilastri perimetrali                 0,6x1,2m
Piastra                                  spessore 1m
Carichi applicati                    F = 10,31 KN; F/2 = 5,15 KN; F/4 = 2,58 KN
M_max (pilastro)                     10117,68 KNm

Con il momento massimo agente sulla piastra andiamo a dimensionare le travi del graticcio: 
​scegliamo un interasse delle travi del graticcio pari a 2,5 m e calcoliamo il momento di inerzia di una striscia di piastra alta 1 m e larga 2,5 m. 
I_x = (bh³)/12 = (2,5mx1³m³)/12 = 0,208 m⁴
Imponiamo che la piastra e il graticcio siano equivalenti in rigidezza e che quindi il momento di inerzia della piastra sia lo stesso del graticcio. Impostiamo una base arbitraria, pari a 0,4 m, e calcoliamo l’altezza utile delle travi del graticcio:
h_u = [(12I_x)/b]^1/3 = [(12x0,208 m⁴)/0,4m] ^1/3 = 1,84 m

Su Sap andiamo a modellare le travi del graticcio con una sezione di 0,4x1,8 m e poste ad un interasse di 2,5 m. Modelliamo le travi come incastrate in ogni nodo, in modo che si riduca l’inflessione delle singole travi. 

A questo punto applichiamo nuovamente i carichi in base all’area di influenza.
Facciamo partire l’analisi con il carico applicato e il peso proprio e visualizziamo la deformata e i diagrammi del momento.

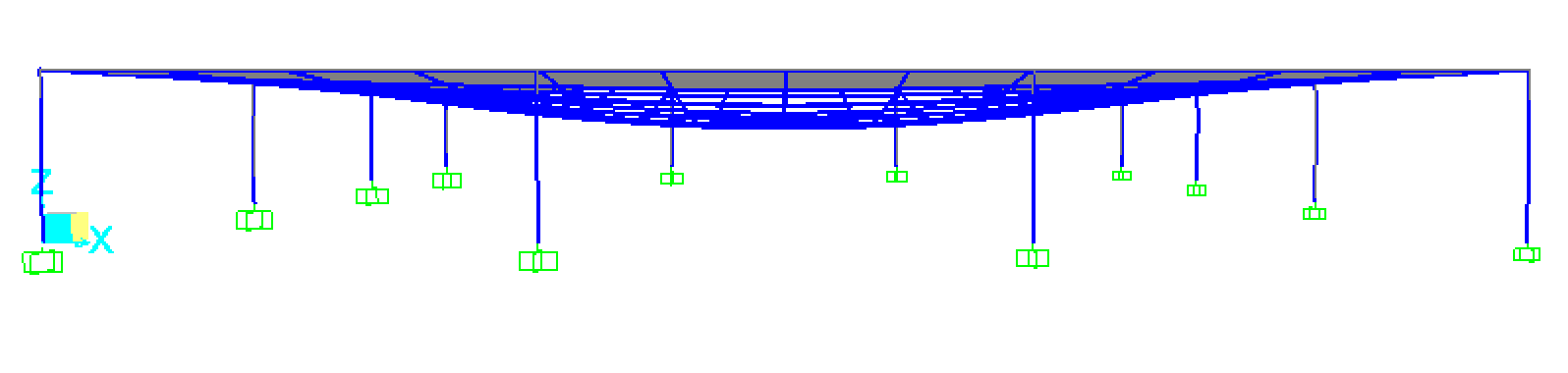
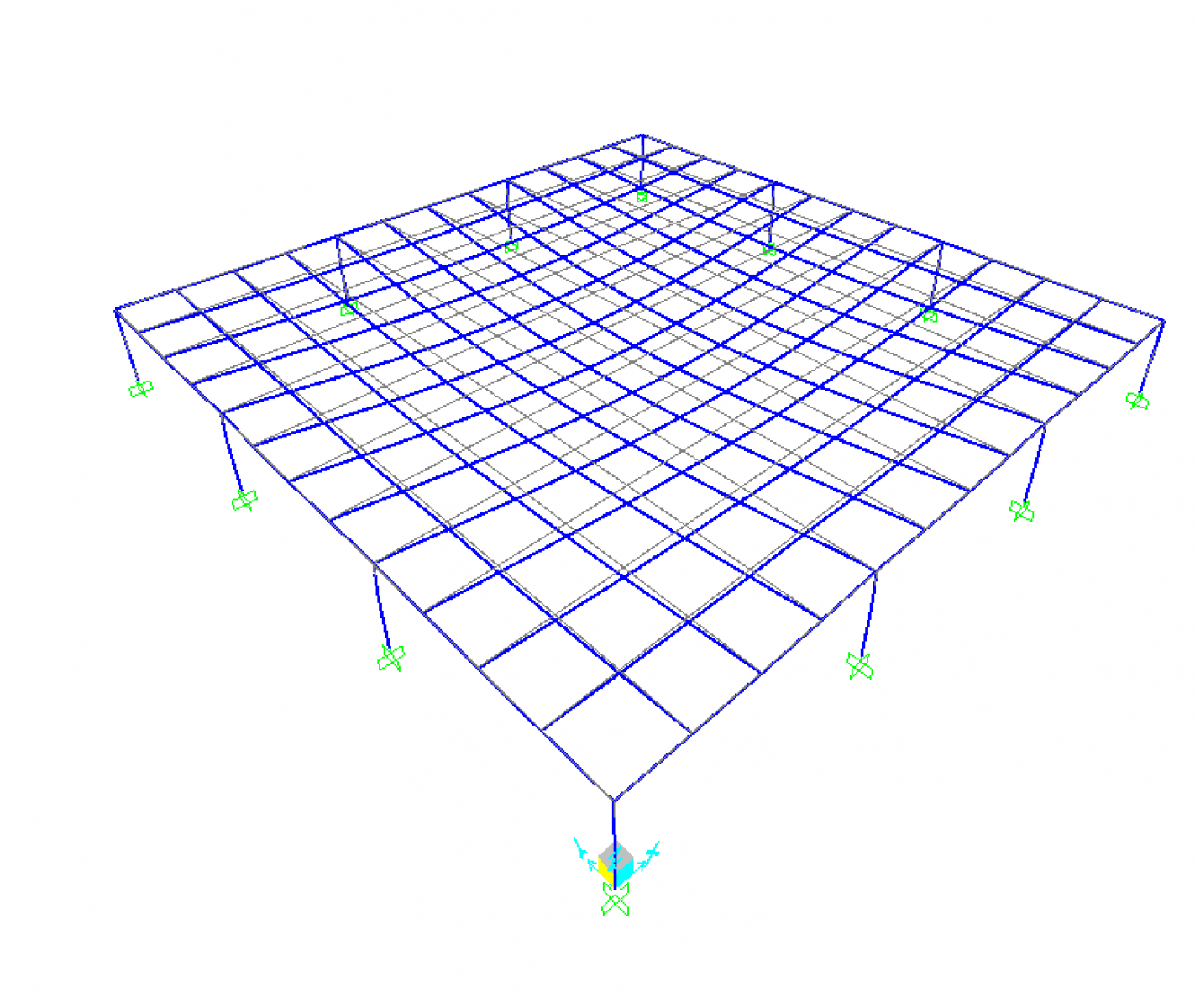
Seconda analisi
Pilastri angolari                     1x1 m
Pilastri perimetrali                 0,6x1,2 m
Travi graticcio                       0,4x1,8 m
Carichi applicati                    F = 257,75 KN; F/2 = 128,87 KN; F/4 = 64,44 KN
M_max-pilastro                        10362,5 KNm
M_max-trave                            10971,2 KNm
M_{max-trave bordo}                   1793 KNm

A questo punto andiamo a verificare cosa succede nel momento in cui aumentiamo la rigidezza della trave di bordo del graticcio: 

Terza analisi
Pilastri angolari                       1x1 m
Pilastri perimetrali                   0,6x1,2 m
Travi di bordo graticcio           1x1,8 m
Carichi applicati                      F = 257,75 KN; F/2 = 128,87 KN; F/4 = 64,44 KN
M_max-pilastro                           10595,58 KNm
M_max-trave                               7438,85 KNm
M_{max-trave bordo}                      3507 KNm

Notiamo quindi che all’aumentare della rigidezza torsionale della trave di bordo diminuisce sensibilmente il momento sulla trave in prossimità del pilastro mentre invece il momento sul pilastro risulta di poco minore rispetto a quello che si verificava con una trave di bordo meno rigida.

A questo punto possiamo effettuare una verifica di resistenza dei pilastri: verifichiamo i pilastri a flessione retta poiché l’eccentricità, data dal rapporto tra il momento agente e lo sforzo normale, è di molto superiore a h/6. 

Risulta che i pilastri così dimensionati non sono verificati a flessione: andiamo quindi ad aumentarne la sezione e rifacciamo l’analisi. 

Quarta analisi
Pilastri angolari                     1x1 m
Pilastri perimetrali                 0,6x1,8 m
Travi di bordo graticcio         1x1,8 m
Carichi applicati                    F = 257,75 KN; F/2 = 128,87 KN; F/4 = 64,44 KN
M_max-pilastro                         14595,98 KNm
M_max-trave                             9527,34 KNm
M_{max-trave bordo}                    3050 KNm

Notiamo che aumentando la sezione del pilastro diminuiscono sia il momento sulla trave di bordo che su quella in prossimità del pilastro. 
Osserviamo anche che il momento massimo sulla trave in prossimità del pilastro ottenuto dall’ultima analisi si avvicina abbastanza a quello ricavato simulando il graticcio con il modello di piastra. 

A questo punto verifichiamo che la trave di bordo resista a torsione. Il momento torcente massimo sulla trave che risulta dall’analisi è pari a 3973,16 KNm.

Verifichiamo che la tensione tangenziale massima sia minore della tensione ammissibile del calcestruzzo compresso: 
τ_max= (αxM_t)/ba²=(4,296x3973,16x10³Nm)/2,5x1,8²m²=2,19 MPa con α=3+1,8(a/b)=3+1,8(1,8m/2,5m)=4,296
τ_max < 8MPa

Effettuiamo dunque una verifica di deformabilità per assicurarci che l’abbassamento della struttura sia minore di quello ammissibile. Gli abbassamenti maggiori si verificano verso il centro del graticcio, dove il valore massimo risulta -0,05278 m con applicata una combinazione di carico allo SLU (q_u=10,31kNm^-2).
L’abbassamento che si verifica sulla struttura risulta minore di l/200 anche con applicato il carico allo SLU quindi consideriamo superata la verifica di abbassamento poiché il carico applicato allo SLE sarebbe di molto minore (6,1 kNm^-2). 

L’esercitazione prevede il dimensionamento di massima e la verifica di una trave Vierendeel costituita da una serie di travi continue, caratterizzate da un’infinita rigidezza flessionale, e una serie di montanti verticali infinitamente rigidi sia assialmente che flessionalmente. Abbiamo ipotizzato tre travi Vierendeel composte ciascuna da quattro campate di 3,50x3,50 m e  poste ad un interasse di 5,00 m l’una dall’altra. Poiché il modello ideale semplificato di trave Vierendeel è assimilabile ad un telaio shear – type ruotato di 90° possiamo risolvere la statica della struttura. 

Per quanto riguarda l’analisi dei carichi abbiamo fatto riferimento al dimensionamento effettuato per la prima esercitazione di un solaio in laterocemento con destinazione ad uso uffici, tenendo in considerazione la combinazione fondamentale di carico allo SLU con coefficienti parziali di sicurezza sfavorevoli.

q_u= γ_G1 x G₁ + γ_G2 x G₂ + γ_Q2 x Q₁= 1,3 x 1,70 + 1,5 x 3,40 + 1,5 x 2,00 =10,30 kNm^-2

Per ottenere i valori delle forze concentrate agenti sui singoli pilastri moltiplichiamo il carico uniformemente distribuito appena calcolato per l’interasse tra i pilastri e per la loro luce. 

A questo punto predimensioniamo i correnti e i pilastri delle Vierendeel e le travi secondarie. 

Andiamo ad impostare la struttura su Sap: modelliamo la geometria delle travi Vierendeel e assegniamo i diaphragm constraints a tutti i nodi affinchè abbiano il comportamento di nodi rigidi. Modelliamo poi i setti come gusci con comportamento membranale, vincolati alla base e nel punto di collegamento con le Vierendeel da degli incastri. A questo punto assegniamo le sezioni predimensionate alle travi e ai pilastri utilizzando un calcestruzzo C28/35. 
Assegniamo quindi i carichi puntiformi precedentemente calcolati in corrispondenza dei pilastri. 

Facciamo quindi partire l’analisi per ricavare i diagrammi e i valori delle sollecitazioni agenti sulla struttura.
Risulta inoltre che i valori del taglio e del momento calcolati risolvendo la statica risultano, seppur approssimati, corrispondenti con quelli determinati da Sap.

A questo punto esportiamo le tabelle delle sollecitazioni e procediamo alla verifica degli elementi strutturali: verifichiamo che la tensione agente sulle travi inflesse e sui pilastri pressoflessi sia minore della tensione di rottura. 

La struttura risulta interamente verificata.

Effettuiamo ora una verifica di deformabilità per assicurarci che l’abbassamento della struttura sottoposta al carico sia minore di quello massimo ammissibile. 
Calcoliamo quindi il carico allo SLE considerando una combinazione di carico frequente: 
q_e= G₁ + G₂ + ψ_1j x Q₁= 1,70 + 3,40 + 0,5 x 2,00 = 6,1 kNm^-2 
Calcoliamo quindi le deformazioni utilizzando le formule ricavate in precedenza dalla rigidezza traslante della trave, che mette in relazione forza e spostamento.

Risulta che l'abbassamento totale della struttura rispetta i limiti di normativa.

L’esercitazione prevede il calcolo e l’applicazione di una forza agente in direzione orizzontale, quale può essere il sisma o il vento, sull’edificio multipiano analizzato per la seconda esercitazione. Si ipotizza che la struttura sia realizzata in c. a. ordinario, con un calcestruzzo di classe di resistenza C 28/35 ed acciaio B 450 C per l’armatura. Il telaio è costituito da travi principali 30x50 cm e pilastri 40x40 cm. 
All’interno della struttura individuiamo nove telai, cinque paralleli all’asse y e quattro paralleli all’asse x. 
Calcoliamo quindi la rigidezza traslante di ogni telaio come rapporto tra il taglio che sollecita il generico pilastro (vale 12EI/L³ per il pilastro doppiamente incastrato come quello del telaio shear-type) e lo spostamento trasversale unitario del suo estremo libero.

Calcoliamo la posizione del baricentro delle masse che, nel caso di carichi uniformemente distribuiti, coincide con il baricentro geometrico e quindi, nel nostro caso, con il punto di intersezione delle diagonali del rettangolo. 

Andiamo ora a calcolare la posizione del baricentro delle rigidezze, il punto in cui applicheremo la forza orizzontale dovuta al sisma calcolata lungo x e lungo y. La posizione del baricentro delle rigidezze dipende innanzitutto dalla posizione dei pilastri in pianta, quindi dalla loro distanza dall’origine di un sistema di riferimento arbitrario (O), ma anche dalla sezione e dall’orientamento dei pilastri stessi e quindi dal momento di inerzia che determina la rigidezza traslante di ogni telaio. 

Definiamo ora i carichi da applicare alla struttura. 
Andiamo innanzitutto a calcolare i carichi permanenti e accidentali gravanti sulla struttura:
q_p=(G₁+G₂)A_tot
q_a=Q₁A_tot
Utilizziamo quindi la combinazione sismica fornita dalla normativa per calcolare i pesi sismici:
W=q_p+q_aψ_2j
con ψ_2j, coefficiente di combinazione per i carichi accidentali, pari a 0,3 per la categoria uffici. 
Una volta calcolati i pesi sismici li moltiplichiamo per il coefficiente di intensità sismica per ottenere la forza sismica orizzontale. Il valore del coefficiente di intensità sismica tiene conto della sismicità del luogo e varia quindi in base alla localizzazione dell’edificio: per la zona di Piramide a Roma è compreso tra 0,150 e 0,175.

A questo punto andiamo a calcolare la ripartizione della forza sismica lungo le due direzioni, x e y. Nel nostro caso il baricentro delle masse e quello delle rigidezze hanno la stessa ordinata quindi applicando la forza sismica lungo x non si genera momento torcente, e di conseguenza la rotazione dell’impalcato, ma solo uno spostamento traslazionale puro. La forza sismica lungo y genera, invece, oltre ad una traslazione verticale, anche una rotazione dell’impalcato dovuta alla presenza di momento torcente generato dall’eccentricità tra l’ascissa del centro delle masse e quella del centro delle rigidezze. 

Utilizzando il modello della seconda esercitazione andiamo ad applicare su Sap2000 le forze sismiche. Poiché la forza sismica si distribuisce linearmente lungo l’altezza dell’edificio calcoliamo la forza applicata ad ogni piano:
F_hi=F_s(h_i/Σ_i) 
Applichiamo come carichi puntiformi al centro delle masse di ogni impalcato i valori delle forze sismiche. Facciamo partire quindi l’analisi con la combinazione di carico allo SLU, il peso proprio della struttura e la forza sismica in direzione x e y. 

Visualizziamo le deformate della struttura quando agiscono le diverse combinazioni di carico.
La deformata della struttura quando agiscono, oltre ai carichi, le forze sismiche in direzione x: 

 La deformata della struttura quando agiscono, oltre ai carichi, le forze sismiche in direzione y: 

A questo punto, come abbiamo fatto per le altre esercitazioni, esportiamo le tabelle con i valori delle sollecitazioni agenti e verifichiamo i pilastri a pressoflessione.
Mentre nella prima parte dell'esercitazione tutti i pilastri ricadevano nel caso della piccola eccentricità, applicando la forza sismica alcuni di essi ricadono nel caso della media e grande eccentricità. In ogni caso tutti i pilastri continuano ad essere verificati a pressoflessione. 

Ai fini dell’esercitazione abbiamo ipotizzato un edificio multipiano in calcestruzzo armato costituito da un modulo di 5x4 m e un aggetto laterale di 2 m. La struttura a telaio, costituita da travi principali, travi secondarie, pilastri e mensole, si eleva per 8 piani fuori terra. 

Si ipotizza che la struttura sia realizzata in c. a. ordinario, con un calcestruzzo di classe di resistenza C 28/35 ed acciaio B 450 C per l’armatura. 

Calcoliamo preventivamente le resistenze di progetto dei materiali:
- la resistenza di progetto dell’acciaio ridotta, rispetto alla tensione caratteristica di snervamento, di un coefficiente parziale di sicurezza: f_yd=f_yk/ γ_s
- la resistenza di progetto a compressione del calcestruzzo ridotta, rispetto alla resistenza caratteristica cilindrica, di un coefficiente parziale di sicurezza e di un ulteriore coefficiente riduttivo per le resistenze di lunga durata: f_cd= α_ccf_ck/ γ_c

Per quanto riguarda l’analisi dei carichi abbiamo fatto riferimento al dimensionamento effettuato per la prima esercitazione di un solaio in laterocemento con destinazione ad uso uffici, tenendo in considerazione la combinazione fondamentale di carico allo SLU con coefficienti parziali di sicurezza sfavorevoli. 

q_u= γ_G1 x G₁ + γ_G2 x G₂ + γ_Q2 x Q₁= 1,3 x 1,70 + 1,5 x 3,40 + 1,5 x 2,00 =10,30 kNm^-2

Prima di procedere al dimensionamento di massima delle travi principali e secondarie calcoliamo il carico lineare distribuito sulla trave moltiplicando il carico allo SLU ottenuto dall’analisi dei carichi per l’interasse della trave che consideriamo di 4 m per la trave principale e di 1 m per quella secondaria. Andiamo quindi a calcolare il momento massimo agente approssimando il comportamento dell’elemento a quello di una trave doppiamente appoggiata con carico uniformemente distribuito. Il momento massimo si verifica nella mezzeria e ha valore ql²/8, dove q è il carico lineare precedentemente calcolato e l è la luce della trave. 

Procediamo quindi al dimensionamento delle travi: ipotizziamo un valore per la base dell’elemento, pari a 30 cm per le travi principali e a 25 cm per le travi secondarie. Per calcolare l’altezza utile della sezione della trave ipotizziamo una sezione fittizia di solo cls. Costruiamo il diagramma delle tensioni imponendo che il calcestruzzo lavori al massimo e che, quindi, la sua tensione sia pari alla tensione di rottura (fcd); allo stesso modo imponiamo che la tensione dell’acciaio sia pari alla sua tensione di snervamento ridotta di un coefficiente di omogeneizzazione (da normativa pari a 15) che tiene conto dei diversi moduli di elasticità dei due materiali. Attaverso la formula del momento flettente, dato dalla coppia di forze costituita dalla risultante di compressione del cls compresso e dalla risultante di trazione dell’acciaio teso, calcoliamo l’altezza utile della sezione reagente. Quest’ultimo valore, sommato alla dimensione del copriferro posta pari a 5 cm, darà il valore minimo dell’altezza della sezione. 

Procediamo al dimensionamento delle mensole utilizzando l’analisi dei carichi e i materiali già utilizzati per la trave. Calcoliamo il momento agente considerando la mensola come una trave a sbalzo con carico uniformemente ripartito: il momento massimo si verifica in corrispondenza dell’incastro e vale ql²/2. 
Dimensioniamo la sezione ingegnerizzata seguendo gli stessi passaggi delle travi principali e secondarie. 

Dopo aver dimensionato effettuiamo una verifica di abbassamento, quindi allo stato limite di esercizio, per controllare che l’abbassamento della mensola sottoposta al carico sia minore di quello massimo ammissibile. 
Calcoliamo quindi il carico allo SLE considerando una combinazione di carico frequente: 
q_e= G₁ + G₂ + ψ_1j x Q₁= 1,70 + 3,40 + 0,5 x 2,00 = 6,1 kNm^-2 
con il coefficiente di combinazione ψ_1j = 0,5 per la categoria uffici. 
Come per le travi calcoliamo il carico uniformemente distribuito sulla mensola moltiplicando il carico allo SLE per l’interasse e sommando il peso proprio dell’elemento. 
Calcoliamo quindi il momento di inerzia della sezione rettangolare che vale I_x = (b x h³)/12. A questo punto calcoliamo l’abbassamento massimo ammissibile con la formula v_max=(ql⁴)/8EI_x che deriva dall’equazione della linea elastica. A questo punto verifichiamo che l’abbassamento della mensola rispetti i limiti di normativa e che sia quindi minore di 1/250 della luce. 

Dopo aver individuato il pilastro maggiormente sollecitato procediamo al dimensionamento: 
in primo luogo calcoliamo i pesi portati dal pilastro in esame, ovvero quello delle travi principali e secondarie e quello del solaio, e li moltiplichiamo per il numero di piani per ottenere lo sforzo normale agente sul pilastro. Per il calcolo utilizziamo una resistenza di progetto a compressione del calcestruzzo ulteriormente ridotta per tenere conto della fessurazione del cls. 
A questo punto calcoliamo l’area minima e la base minima della sezione del pilastro considerando una sezione quadrata. Essendo il pilastro soggetto a pressoflessione andiamo a ricalcolare la base minima necessaria affinchè l’elemento non vada in instabilità a carico di punta: calcoliamo quindi la luce libera di inflessione del pilastro considerando un coefficiente di inflessione pari a 1 in caso di elemento doppiamente incernierato. Determiniamo dunque la snellezza critica superata la quale l’asta va in instabilità da carico di punta e il raggio di inerzia minimo della sezione grazie al quale otteniamo il valore della base minima del pilastro. Siamo quindi in grado di scegliere base e altezza della sezione del pilastro. 

Dopo aver predimensionato gli elementi che costituiscono il telaio andiamo a impostare e costruire la struttura su SAP2000. Dividiamo gli elementi in gruppi in base alla loro area di influenza. Per quanto riguarda gli elementi orizzontali differenziamo travi principali centrali, travi principali perimetrali, travi secondarie e mensole. Dividiamo invece gli elementi verticali in pilastri centrali, perimetrali e angolari per ogni piano. 
Definiamo e assegniamo i vincoli alla struttura: incastri in corrispondenza dell’attacco a terra e diaphragm constraint al resto della struttura affinchè la struttura si comporti come un telaio a nodi rigidi. Procediamo quindi definendo e assegnando i materiali, le sezioni predimensionate e i carichi agenti sulla struttura. In questo caso, oltre ad assegnare i carichi permanenti e variabili già calcolati con la combinazione di carico allo SLU, introduciamo anche la forza orizzontale del vento, sia in direzione x che in direzione y.  Facciamo quindi partire l’analisi per ricavare i diagrammi e i valori delle sollecitazioni agenti sulla struttura. 

Una volta ricavati i valori delle sollecitazioni grazie al modello di SAP possiamo andare a verificare la struttura.
Per comodità verifichiamo solamente gli elementi piú sollecitati.
Procediamo alla verifica delle travi sottoposte a flessione retta: dobbiamo verificare che la tensione agente su ogni trave sia minore di fcd, ovvero della tensione di rottura del calcestruzzo.

Procediamo ora alla verifica, a flessione per quanto riguarda travi e mensole, e a pressoflessione per quanto riguarda i pilastri: dobbiamo accertarci che la tensione massima agente sia minore della tensione di rottura. Per i pilastri distinguiamo tre casi differenti in base all’eccentricità. 

L'intera struttura risulta verificata.

Ai fini dell’esercitazione abbiamo ipotizzato un edificio con una copertura reticolare alla quale sono stati appesi quattro piani sottostanti. La copertura, di dimensioni 24,00 m x 12,00 m x 3,00 m, è appoggiata su due vani scala costituiti da setti murari in calcestruzzo armato.

Dopo aver disegnato la reticolare su SAP2000 siamo andate a definire e assegnare alla struttura il materiale scelto per i profili delle aste, nel nostro caso l'acciaio S275. Abbiamo poi definito e assegnato alle aste una sezione provvisoria di tubo in acciaio a sezione circolare dal profilario integrato di SAP: andremo successivamente a dimensionare correttamente le sezioni dopo aver calcolato il valore degli sforzi su ogni asta. 
Siamo andate quindi ad assegnare i vincoli, sia le cerniere esterne in corrispondenza degli appoggi della struttura, sia le cerniere esterne impostando il rilascio dei momenti all'inizio e alla fine di ogni asta.

Andiamo quindi a definire i carichi da assegnare ai nodi della struttura, senza considerarne il peso proprio. Innanzitutto abbiamo calcolato le azioni agenti sulla struttura distinguendole in base alla loro intensità nel tempo.

 Si è poi tenuta in considerazione la combinazione fondamentale di carico usata per le verifiche allo SLU con coefficienti parziali di sicurezza sfavorevoli. 
Il peso totale risulta quindi: q_u= γ_G1 x G₁ + γ_G2 x G₂ + γ_Q2 x Q₁= 1,3 x 1,70 + 1,5 x 3,40 + 1,5 x 2,00 =10,30 kNm^-2
Andiamo a calcolare il carico ripartito su ogni nodo in base alla sua area di influenza e alla sua posizione in pianta. Su ciascun pilastro gravano i carichi disposti nella sua area di influenza quindi in definitiva sui pilastri agirà una forza pari a:

Assegniamo quindi su SAP2000 le forze puntiformi che agiscono sui nodi della struttura. 
Facciamo partire l'analisi: otteniamo la conformazione deformata e i valori delle sollecitazioni e degli abbassamenti.

Esportiamo le tabelle delle sollecitazioni e andiamo ad individuare le aste maggiormente soggette a compressione e a trazione.

Andiamo quindi a dimensionare le aste soggette a trazione: calcoliamo l’area minima del profilo data dal rapporto tra lo sforzo normale agente sull’asta e la resistenza di calcolo dell’acciaio S275.
A_min = N*fyk/γ_m
Dopo aver scelto il profilario di riferimento cerchiamo un profilo che abbia un’area leggermente maggiore dell’area minima calcolata. Per comodità abbiamo suddiviso le aste tese in 6 gruppi in base alla sollecitazione agente.

Dimensioniamo ora le aste soggette a compressione allo stesso modo di quelle a trazione. Dobbiamo però verificare che le aste non subiscano fenomeni di instabilità a carico di punta. Andiamo quindi a calcolare il raggio di inerzia minimo della sezione e la snellezza critica della sezione, ovvero la snellezza limite superata la quale l’asta va in instabilità.
λ = π  √ (E / fyd)
ρ_min = β*l / λ
I_min = A_min*(ρ_min)²
Andiamo quindi a cercare sul profilario una sezione che abbia non solo area leggermente superiore a quella minima ma anche un raggio di inerzia maggiore di quello minimo calcolato. Come per le aste tese abbiamo individuato 6 profili differenti per le aste compresse. 

Andiamo ad assegnare su SAP alle aste le sezioni correttamente dimensionate: per comodità assegniamo a tutte le aste una sezione tubolare che ha come area una media delle sezioni dimensionate con gli sforzi ottenuti dall’analisi del modello. 

A questo punto calcoliamo il peso proprio della struttura: su SAP facciamo un’analisi con il solo carico DEAD che ha come Self Weight Multiplier 1 e si comporta dunque come carico uniformemente distribuito. Tramite i valori delle reazioni vincolari in corrispondenza delle cerniere esterne riusciamo ad ottenere un valore molto vicino a quello reale del peso proprio. Esportando la tabella delle reazioni vincolari e sommando i valori di quelle verticali otteniamo quindi il peso proprio della struttura. 

Con il valore ottenuto andiamo a definire un nuovo caso di carico, PP, con moltiplicatore 0 perchè andremo ad assegnarlo come carico concentrato. Andiamo ad applicare i carichi sui nodi: dopo aver diviso il valore totale del peso proprio per il numero di nodi applichiamo questo carico ai nodi centrali, ai nodi laterali la metà del carico applicato sui nodi centrali e agli angolari 1/4 del carico applicato sui nodi centrali.

Creiamo una nuova combinazione di carico data dalla somma del peso proprio della struttura e il carico allo SLU: facendo partire l’analisi ed esportando le tabelle delle sollecitazioni con questa combinazione di carico dovremmo avere un risultato non molto differente da quello ottenuto con il solo carico allo SLU poiché l’influenza del peso proprio sulle strutture in acciaio non è particolarmente rilevante. 

Di contro, però, le strutture in acciaio sono caratterizzate da elevata deformabilità se sottoposte a carichi ed è quindi necessario effettuare verifiche di deformabilità in condizioni di esercizio. 
Calcoliamo quindi la combinazione fondamentale di carico allo SLE che ha coefficienti di sicurezza più bassi rispetto allo SLU:
q_e= γ_G1 x G₁ + γ_G2 x G₂ + γ_Q2 x Q₁= 1,00 x 1,70 + 0,7 x 3,40 + 0,7 x 2,00 = 5,50 kNm^-2
Il carico totale allo SLE risulta quindi: 5,50 kNm^-2 x 288 m^-2x 4 piani = 6336 kN
Come abbiamo fatto in precedenza assegniamo il carico allo SLE ai nodi e facciamo un’analisi delle sollecitazioni agenti sulla struttura nel caso di una combinazione di carico PP+ q_e. 
Esportiamo quindi la tabella che mostra lo spostamento dei nodi rispetto alla posizione iniziale: per normativa gli spostamenti verticali per le coperture devono essere inferiori a L/200 dove L è la luce maggiore tra l'appoggio e il nodo. 

Verifichiamo che 0,0297 m sia inferiore a L/200, con L pari a 18 m. Nel nostro caso la verifica di abbassamento è soddisfatta dato che 0,0297 m < 0,09 m.