Esercitazione 2_Sisma - Crisciotti, Latour, Zampilli

L’esercitazione prevede il calcolo e l’applicazione di una forza agente in direzione orizzontale, quale può essere il sisma o il vento, sull’edificio multipiano analizzato per la seconda esercitazione. Si ipotizza che la struttura sia realizzata in c. a. ordinario, con un calcestruzzo di classe di resistenza C 28/35 ed acciaio B 450 C per l’armatura. Il telaio è costituito da travi principali 30x50 cm e pilastri 40x40 cm. 
All’interno della struttura individuiamo nove telai, cinque paralleli all’asse y e quattro paralleli all’asse x. 
Calcoliamo quindi la rigidezza traslante di ogni telaio come rapporto tra il taglio che sollecita il generico pilastro (vale 12EI/L³ per il pilastro doppiamente incastrato come quello del telaio shear-type) e lo spostamento trasversale unitario del suo estremo libero.

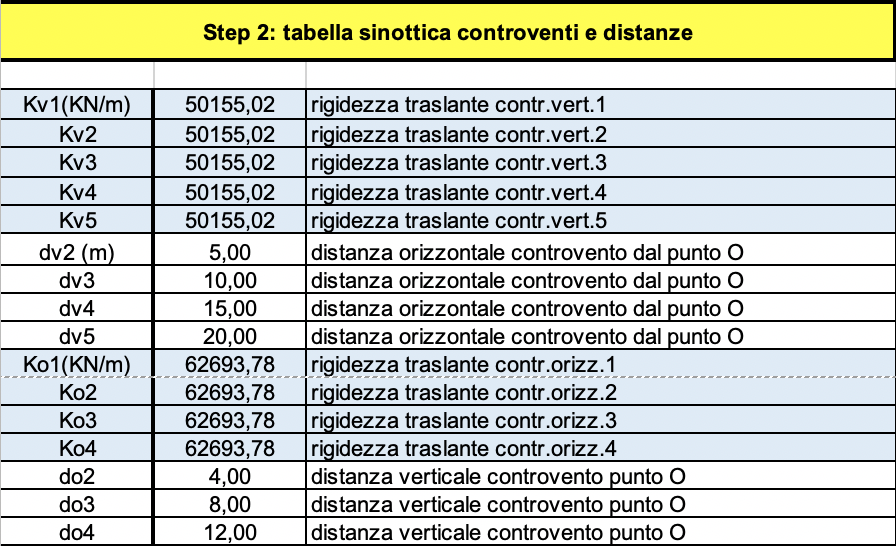
Calcoliamo la posizione del baricentro delle masse che, nel caso di carichi uniformemente distribuiti, coincide con il baricentro geometrico e quindi, nel nostro caso, con il punto di intersezione delle diagonali del rettangolo. 

Andiamo ora a calcolare la posizione del baricentro delle rigidezze, il punto in cui applicheremo la forza orizzontale dovuta al sisma calcolata lungo x e lungo y. La posizione del baricentro delle rigidezze dipende innanzitutto dalla posizione dei pilastri in pianta, quindi dalla loro distanza dall’origine di un sistema di riferimento arbitrario (O), ma anche dalla sezione e dall’orientamento dei pilastri stessi e quindi dal momento di inerzia che determina la rigidezza traslante di ogni telaio. 

Definiamo ora i carichi da applicare alla struttura. 
Andiamo innanzitutto a calcolare i carichi permanenti e accidentali gravanti sulla struttura:
q_p=(G₁+G₂)A_tot
q_a=Q₁A_tot
Utilizziamo quindi la combinazione sismica fornita dalla normativa per calcolare i pesi sismici:
W=q_p+q_aψ_2j
con ψ_2j, coefficiente di combinazione per i carichi accidentali, pari a 0,3 per la categoria uffici. 
Una volta calcolati i pesi sismici li moltiplichiamo per il coefficiente di intensità sismica per ottenere la forza sismica orizzontale. Il valore del coefficiente di intensità sismica tiene conto della sismicità del luogo e varia quindi in base alla localizzazione dell’edificio: per la zona di Piramide a Roma è compreso tra 0,150 e 0,175.

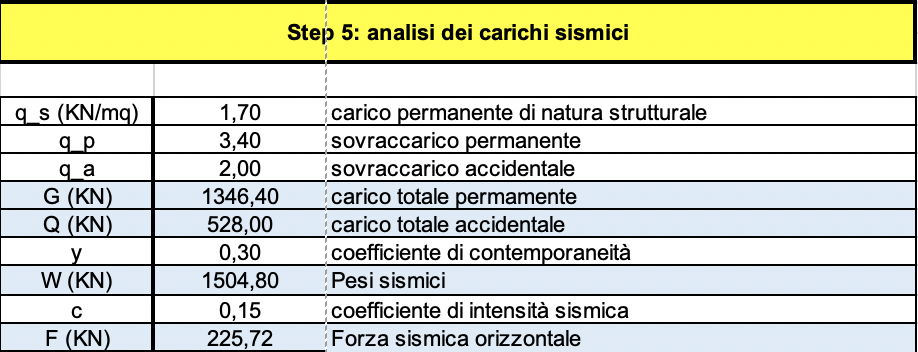
A questo punto andiamo a calcolare la ripartizione della forza sismica lungo le due direzioni, x e y. Nel nostro caso il baricentro delle masse e quello delle rigidezze hanno la stessa ordinata quindi applicando la forza sismica lungo x non si genera momento torcente, e di conseguenza la rotazione dell’impalcato, ma solo uno spostamento traslazionale puro. La forza sismica lungo y genera, invece, oltre ad una traslazione verticale, anche una rotazione dell’impalcato dovuta alla presenza di momento torcente generato dall’eccentricità tra l’ascissa del centro delle masse e quella del centro delle rigidezze. 

Utilizzando il modello della seconda esercitazione andiamo ad applicare su Sap2000 le forze sismiche. Poiché la forza sismica si distribuisce linearmente lungo l’altezza dell’edificio calcoliamo la forza applicata ad ogni piano:
F_hi=F_s(h_i/Σ_i) 
Applichiamo come carichi puntiformi al centro delle masse di ogni impalcato i valori delle forze sismiche. Facciamo partire quindi l’analisi con la combinazione di carico allo SLU, il peso proprio della struttura e la forza sismica in direzione x e y. 

Visualizziamo le deformate della struttura quando agiscono le diverse combinazioni di carico.
La deformata della struttura quando agiscono, oltre ai carichi, le forze sismiche in direzione x: 

 La deformata della struttura quando agiscono, oltre ai carichi, le forze sismiche in direzione y: 

A questo punto, come abbiamo fatto per le altre esercitazioni, esportiamo le tabelle con i valori delle sollecitazioni agenti e verifichiamo i pilastri a pressoflessione.
Mentre nella prima parte dell'esercitazione tutti i pilastri ricadevano nel caso della piccola eccentricità, applicando la forza sismica alcuni di essi ricadono nel caso della media e grande eccentricità. In ogni caso tutti i pilastri continuano ad essere verificati a pressoflessione.