Esercitazione 2- Progetto e verifica di un edificio multipiano in calcestruzzo in zona non sismica_Elena Santacesaria, Benedetta Schettini.

Studentesse: Elena Santacesaria, Benedetta Schettini.

Il fine di questa seconda esercitazione è quello di considerare un edificio multipiano con una struttura composta da telai piani in cls armato (le travi collaborano con i pilastri) e dunque di dimensionare i suoi elementi: travi, pilastri, mensole.

MODELLO

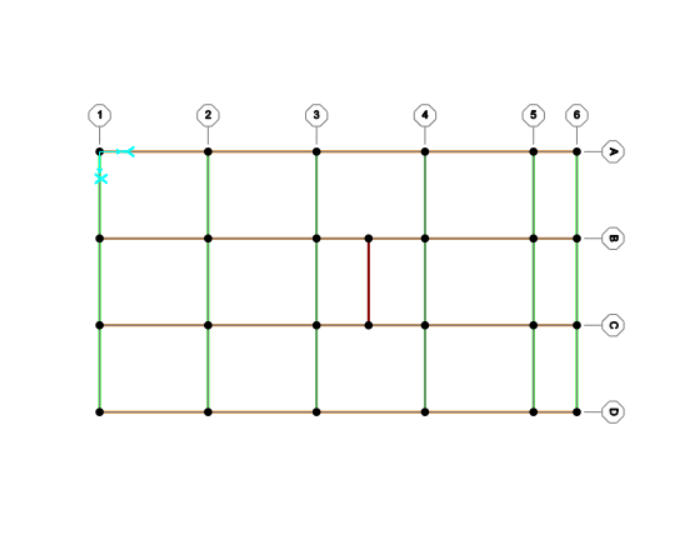
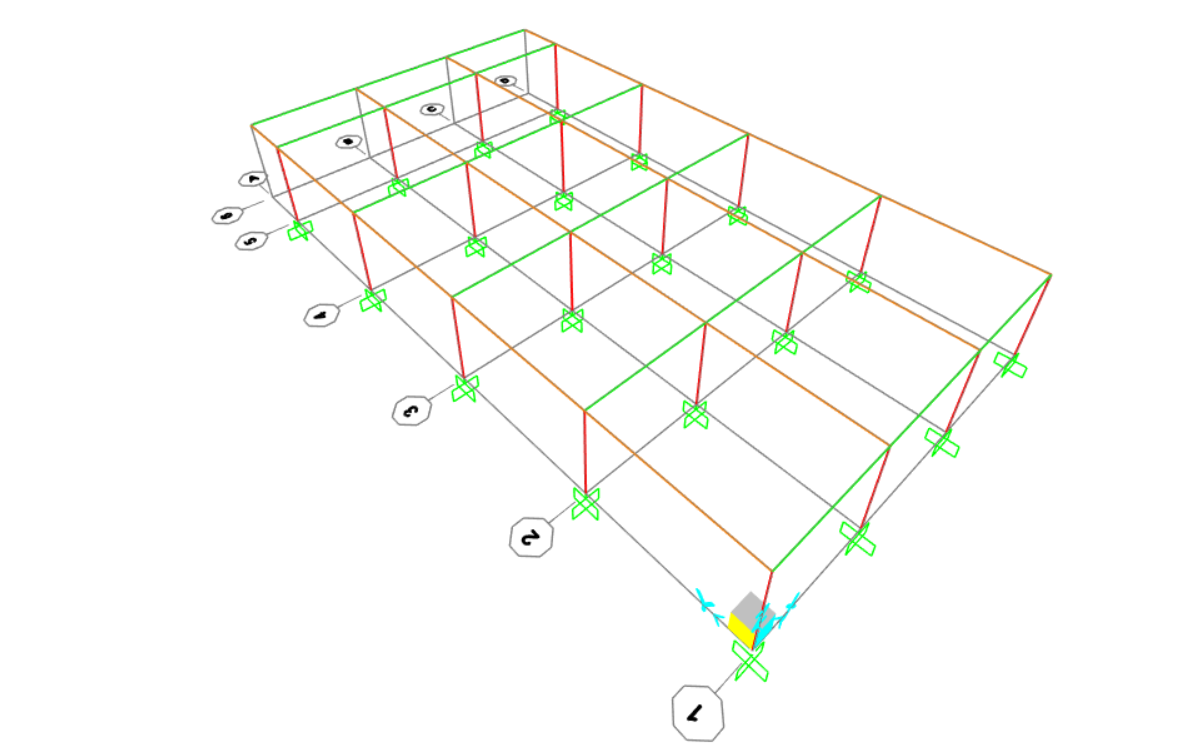
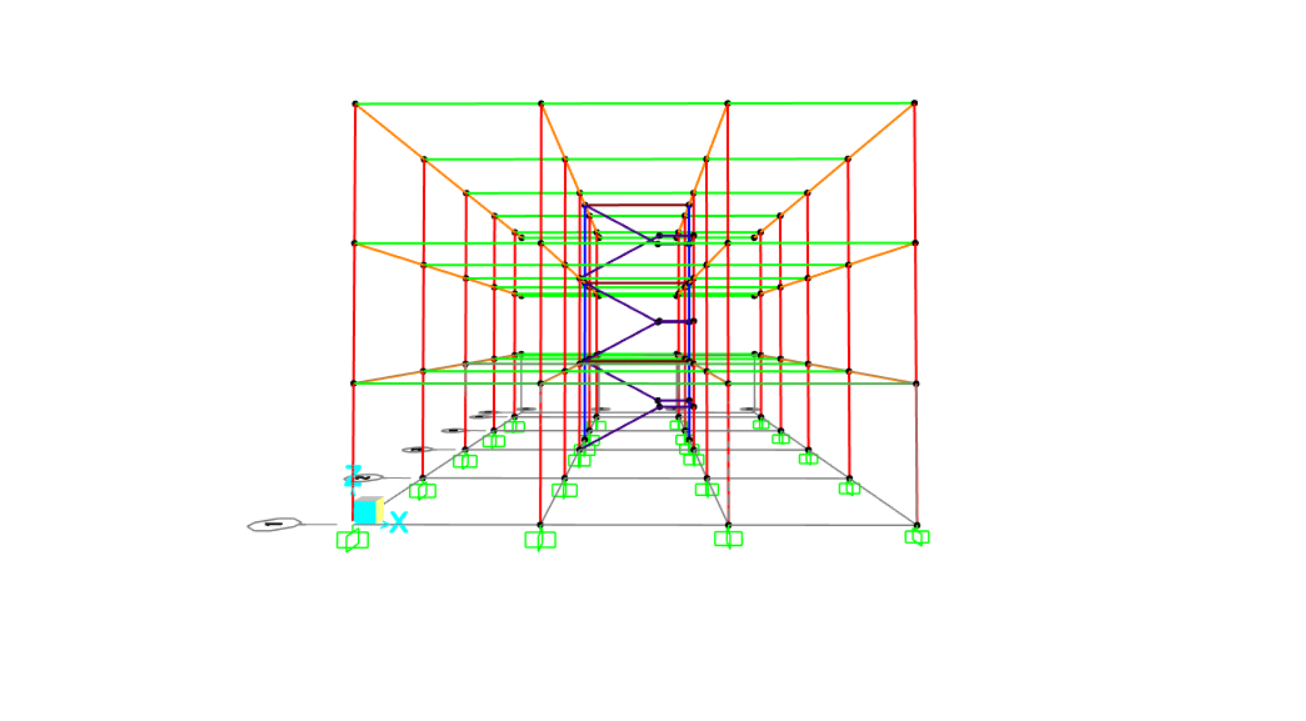
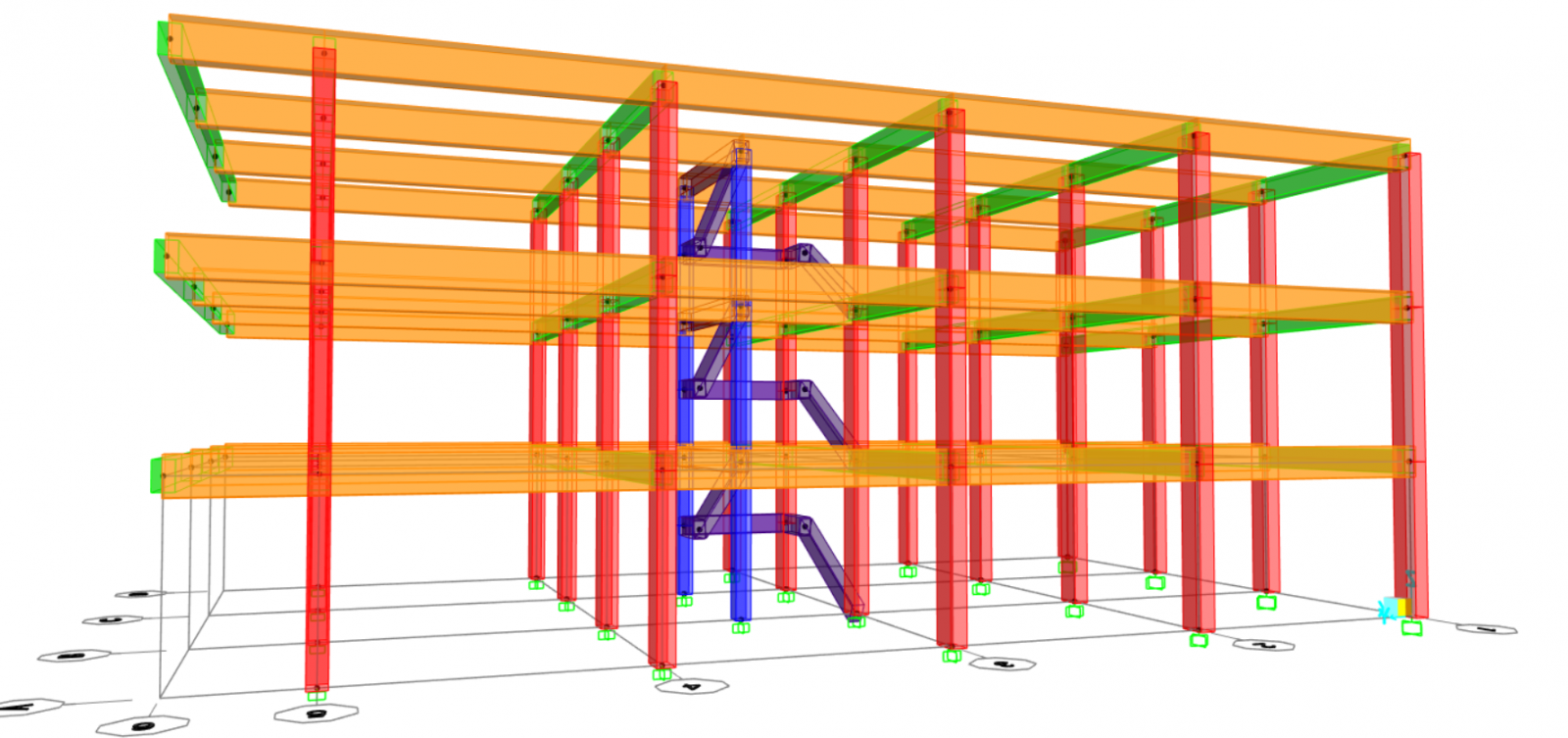
Per prima cosa abbiamo costruito la struttura da analizzare direttamente su SAP2000, partendo da una griglia regolare di 4x3 campate (di 5x4m ciascuna) e uno sbalzo laterale di 2m. La struttura si sviluppa su 3 piani di 3m ciascuno, con un corpo scala centrale. Per la definizione del modello iniziale siamo partite da un'assegnazione preliminare di massima delle sezioni dei vari elementi, che poi verranno adeguatamente verificati. Altro passaggio fondamentale è stato quello di assegnare i vincoli a terra, che in una struttura a telaio rigido in cls sono tutti incastri. Una volta definito il modello siamo passate al predimensionamento degli elementi.

ANALISI DEI CARICHI

Prima di tutto, per poter dimensionare gli elementi, è necessario conoscere il carico q che grava su questi e dunque procedere con l'analisi dei carichi che consente di conoscere l'entità della forza agente sui componenti della struttura. Abbiamo ipotizzato l'utilizzo di un solaio in latero-cemento.
Carico permanente strutturale (travetti, pignatte, soletta):
Qs= 3,5 KN/mq
Carico permanente non strutturale (intonaco, massetto, malta, pavimentazione, incidenza tramezzi):
Qp=3,0 KN/mq
Sovraccarico accidentale (definito in base alla destinazione d'uso, nel nostro caso residenziale):
Qa=2,0 KN/mq

Abbiamo dunque calcolato la combinazione allo SLU con i rispettivi coefficienti: Qu= (Qs*1,3)+(Qp*1,5)+(Qa*1,5) ottenendo: Qu=12,05 KN/mq

PREDIMENSIONAMENTO

Travi
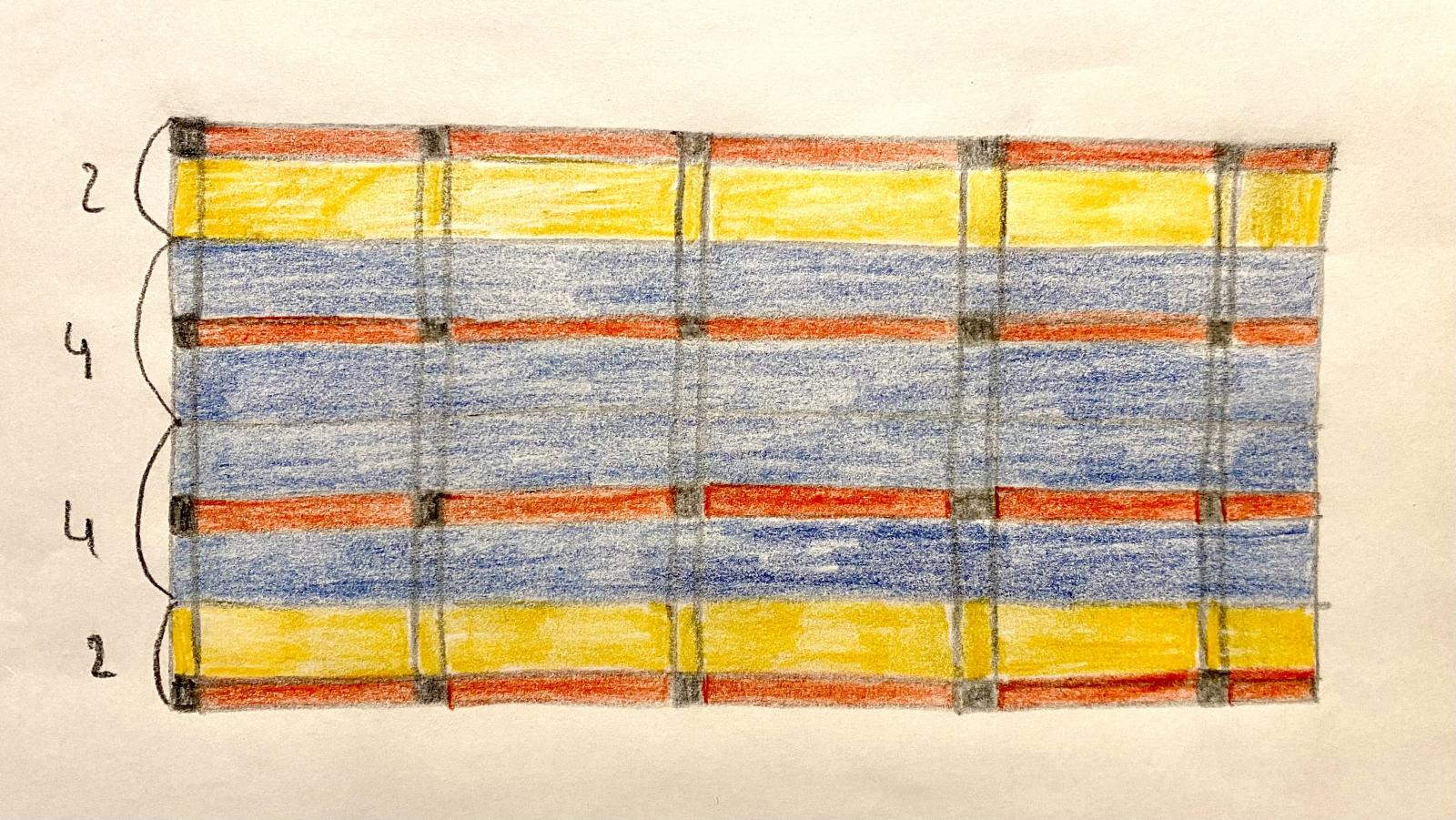
Per prima cosa, ragionando sull'orditura del solaio, abbiamo distinto le travi principali dalle secondarie. Successivamente, in base alle rispettive aree di influenza di solaio agente su di esse, le abbiamo ulteriormente distinte in:
-Travi principali centrali (più sollecitate, hanno l'area di influenza maggiore)
-Travi principali perimetrali (con area di influenza dimezzata)
-Travi secondarie centrali
-Travi secondarie perimetrali

Vedremo in seguito che le travi perimetrali, principali e secondarie, sono soggette ad un carico ulteriore che è quello del tompagno e dunque una suddivisione più corretta sarebbe:
-Travi principali centrali e travi principali perimetrali che portano il tompagno
-Travi secondarie che portano solo se stesse e travi secondarie che portano il tompagno (confermando che non sono mai scariche).

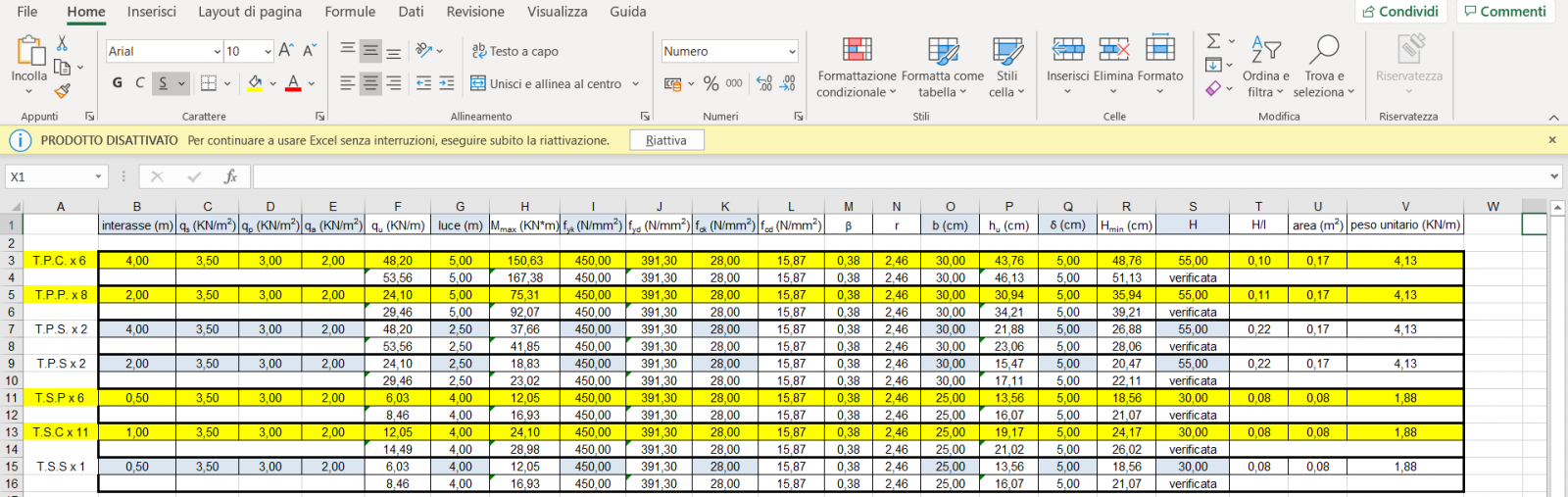
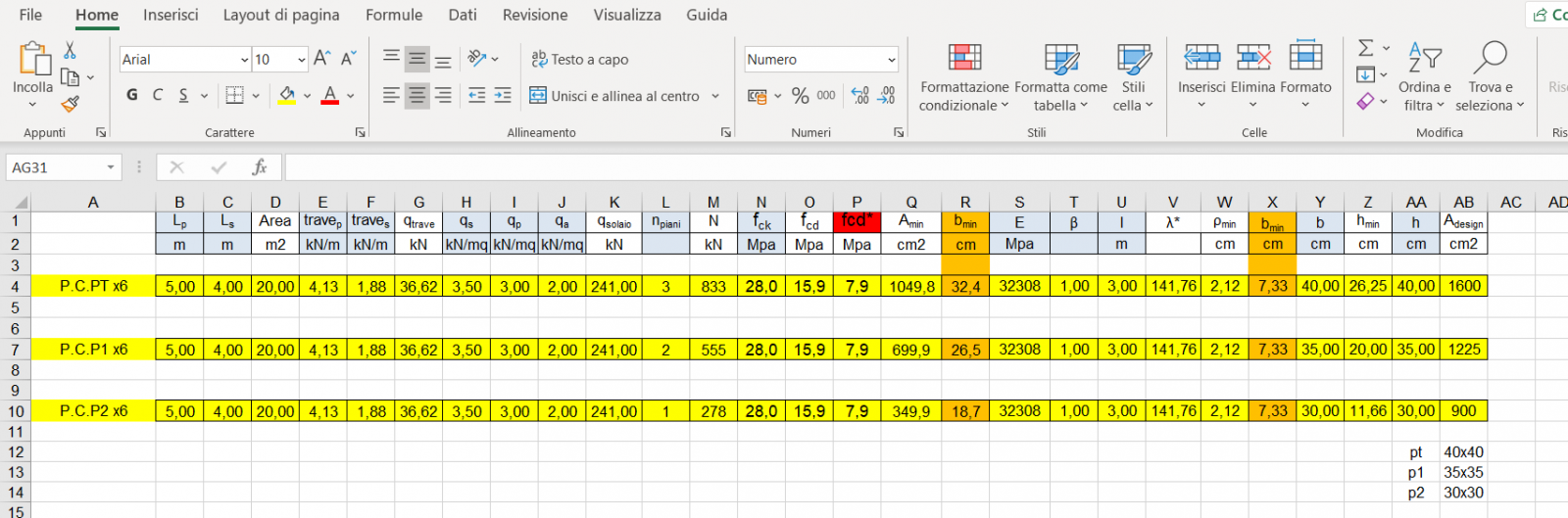
Da queste considerazioni siamo passate su Excel. Una volta calcolato il carico uniformemente distribuito su ogni trave, ricaviamo il momento flettente massimo che agisce su di esse (ricordando che nel caso di una trave doppiamente appoggiata si trova nella sezione di mezzeria e dunque vale: Mmax: (Qu*l^2)/8), il valore della resistenza a compressione del cls (fcd) e quella dell'acciaio di armatura (fck). Tramite questi ultimi valori abbiamo ricavato i parametri β (la cui formula definisce il rapporto tra l'altezza utile hu e l'asse neutro) ed r.
Fissate in precedenza le dimensioni della base, nel nostro caso 30cm sia per le travi principali che secondarie, abbiamo ottenuto l'altezza utile alla quale è stata aggiunta la dimensione del copriferro, per conoscere infine l'altezza minima di progetto, successivamente ingegnerizzata (Hmin=hu+δ). Per ultimi abbiamo calcolato l'area della sezione e subito dopo, conoscendo il peso specifico del cls, il peso unitario, valore importante che è stato sommato al Qu per capire se le dimensioni della sezione consentono alla trave di resistere anche sommando al carico ultimo il peso proprio dell'intero elemento.

Mensole

I medesimi passaggi svolti per il predimensionamento delle travi sono stati eseguiti anche per quanto riguarda le mesole. Definita l'area di influenza ed il carico uniformemente distribuito che grava su di esse, abbiamo raggiunto il valore massimo del momento agente (che non è più quello di una trave doppiamente appoggiata, ma trattandosi di mensole, in corrispondenza della sezione di incastro vale: Mmax=(Qu*l^2)/2). Stabilite le dimensioni della sezione, 30x45cm nel nostro caso, abbiamo effettuato una verifica a deformabilità controllando che l'abbassamento massimo dell'elemento fosse minore del 2% della distanza massima dall'appoggio. Questo procedimento è stato effettuato allo SLE per verificare che non vi siano deformazioni capaci di limitare l'efficienza della costruzione.

Pilastri

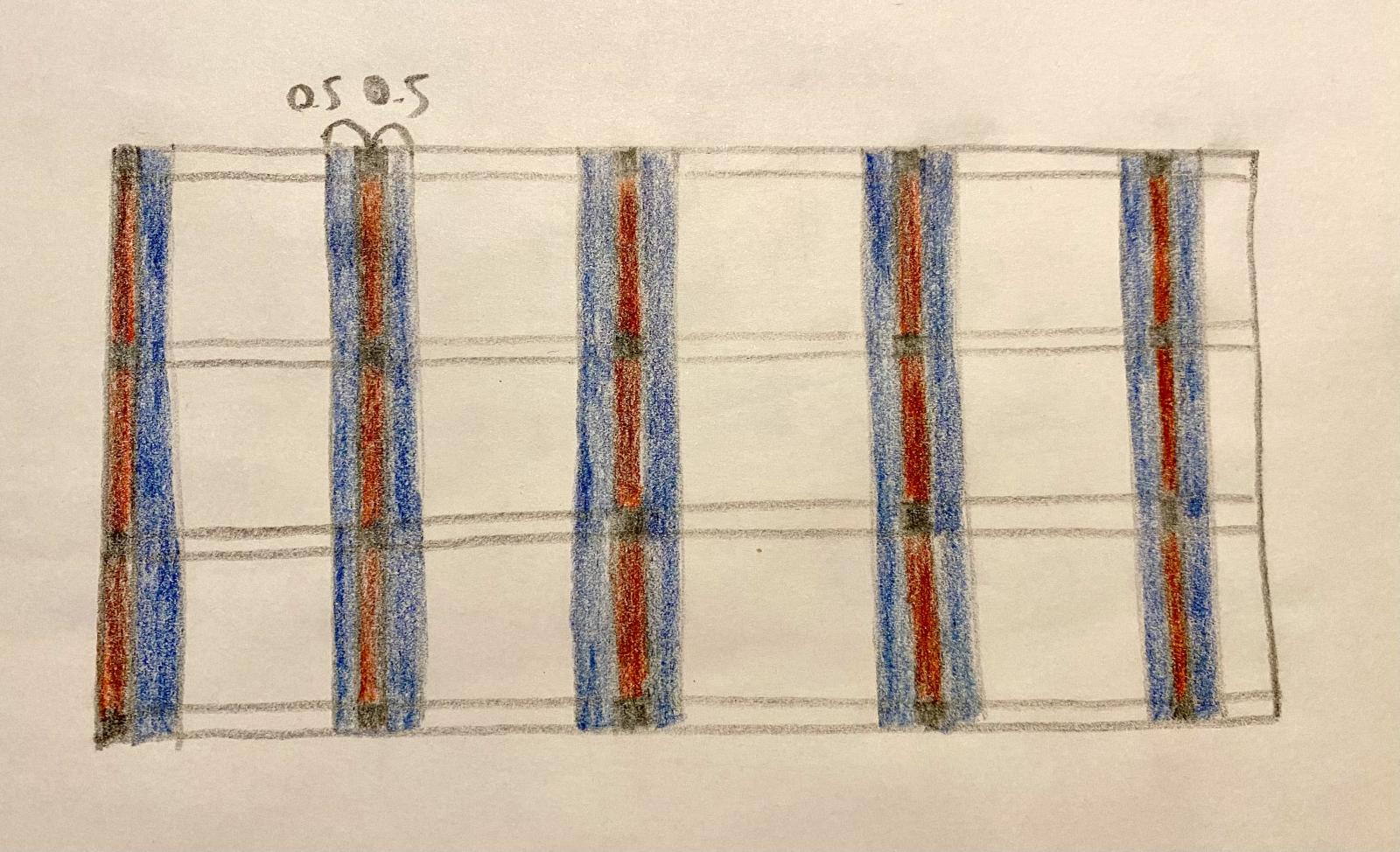
Anche in questo caso è stato fondamentale cominciare con l'individuazione e il calcolo delle varie aree di influenza. Per ogni piano abbiamo distinto 3 categorie di pilastri:
-angolari
-perimetrali 
-centrali (quelli centrali del piano terra saranno sicuramente i più sollecitati poichè su questi verranno trasmessi tutti i carichi dei piani superiori)

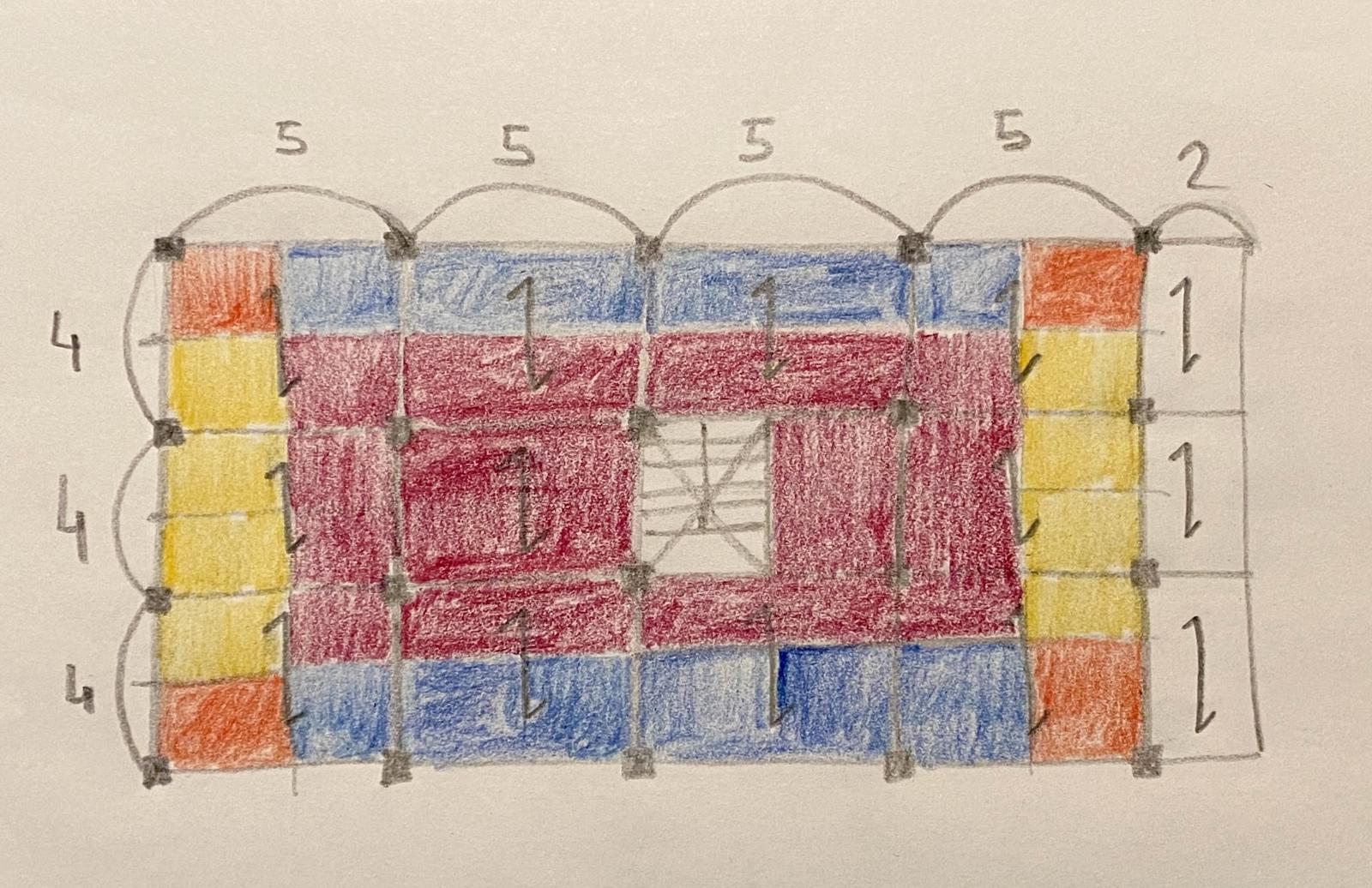
Passando dunque su Excel, nel compilare la tabella questa volta abbiamo dovuto tener conto del fatto che su questi elementi il carico non è uniformemente distribuito, bensì concentrato, e considera la somma dei carichi agenti di solaio, travi principali e secondarie (tiene conto quindi della possibilità di rottura del materiale per schiacciamento e della possibilità che si verifichi il fenomeno di instabilità).

Arriviamo così a definire uno sforzo normale massimo verosimile che dipende dal carico dovuto al peso proprio delle travi che si poggiano in testa al pilastro, dal carico del solaio e dal numero dei piani dell'edificio. A partire dalla resistenza di progetto del materiale fcd, abbiamo ricavato di conseguenza l'area di sezione minima del pilastro affinchè non si verifichi lo schiacciamento del materiale.

Da questo momento in poi è subentrato il concetto di snellezza, e abbiamo dimensionato considerando anche il momento flettente, poichè sappiamo che i pilastri sono elementi soggetti a pressoflessione. Abbiamo stabilito quindi il valore massimo di snellezza, usando la luce libera di inflessione (che tiene conto di come il pilastro è vincolato) e il modulo di elasticità del cls, e da questa il valore minimo del raggio di inerzia necessario al fine di evitare il fenomeno dell'instabilità euleriana.

Determinate quindi la base e l'altezza minima abbiamo definito la sezione effettiva di progetto ed è stato poi necessario verificare a pressoflessione il pilastro, imponendo che la tensione massima a cui è sottoposto siamo minore o uguale alla resistenza di progetto del materiale.

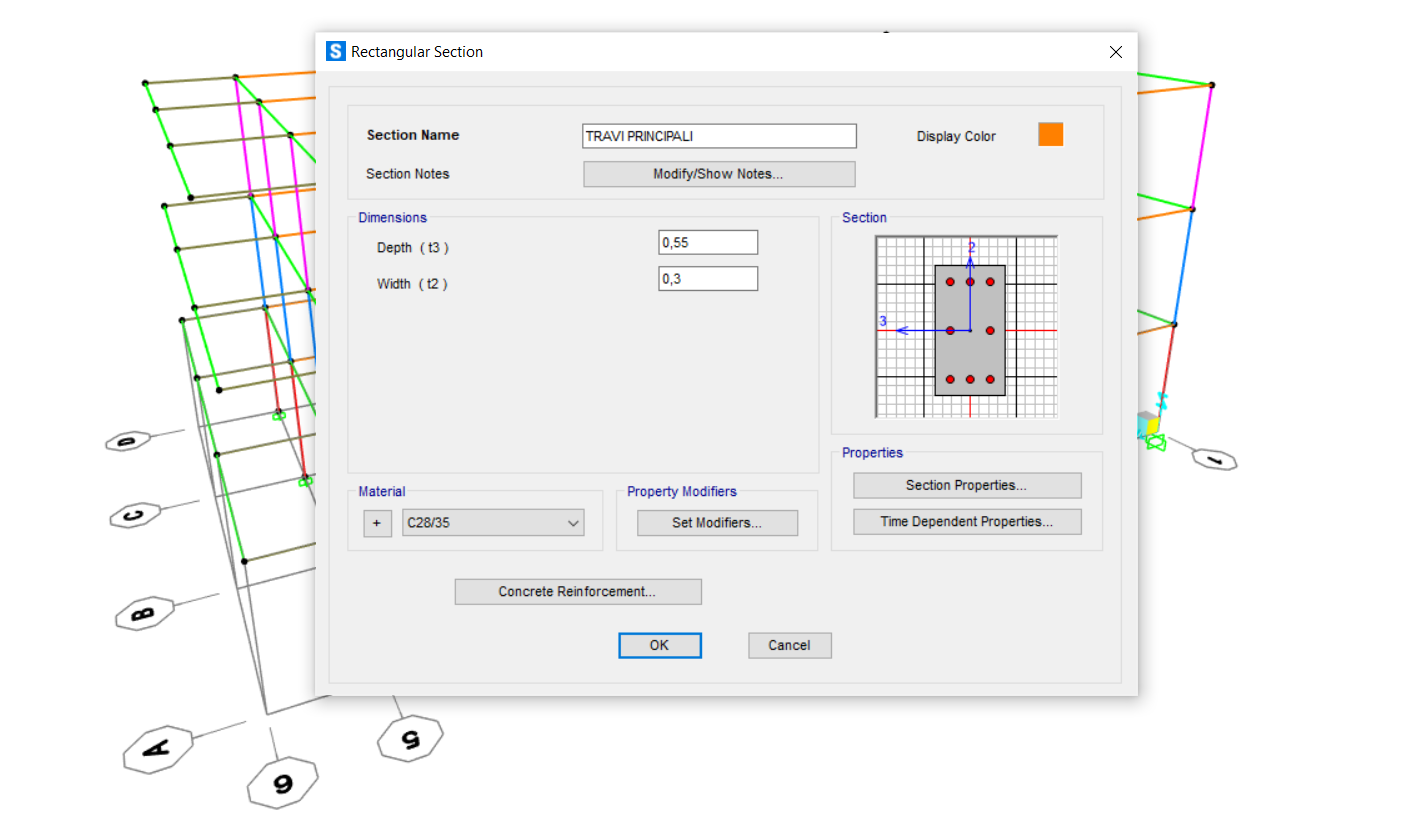
Modello

Dopo aver predimensionato tutti gli elementi del telaio siamo tornate al modello su SAP2000, per agevolare il lavoro abbiamo diviso gli elementi in vari gruppi, e infine riassegnato correttamente le sezione calcolate precedentemente, avendo già definito il materiale. Per assegnare i carichi uniformemente distribuiti abbiamo creato una combinazione di carichi SLU (da Define/Load Combination) che tiene conto dei carichi sopracitati Qs, Qp, Qa, del peso proprio PP degli elementi e del G2, il peso del tompagno che grava sulle travi perimetrali e che è stato aggiunto nella combinazione come carico lineare insieme agli altri. Per ultimo è stato applicato il diaphram per simulare al meglio la condizione di telaio rigido.

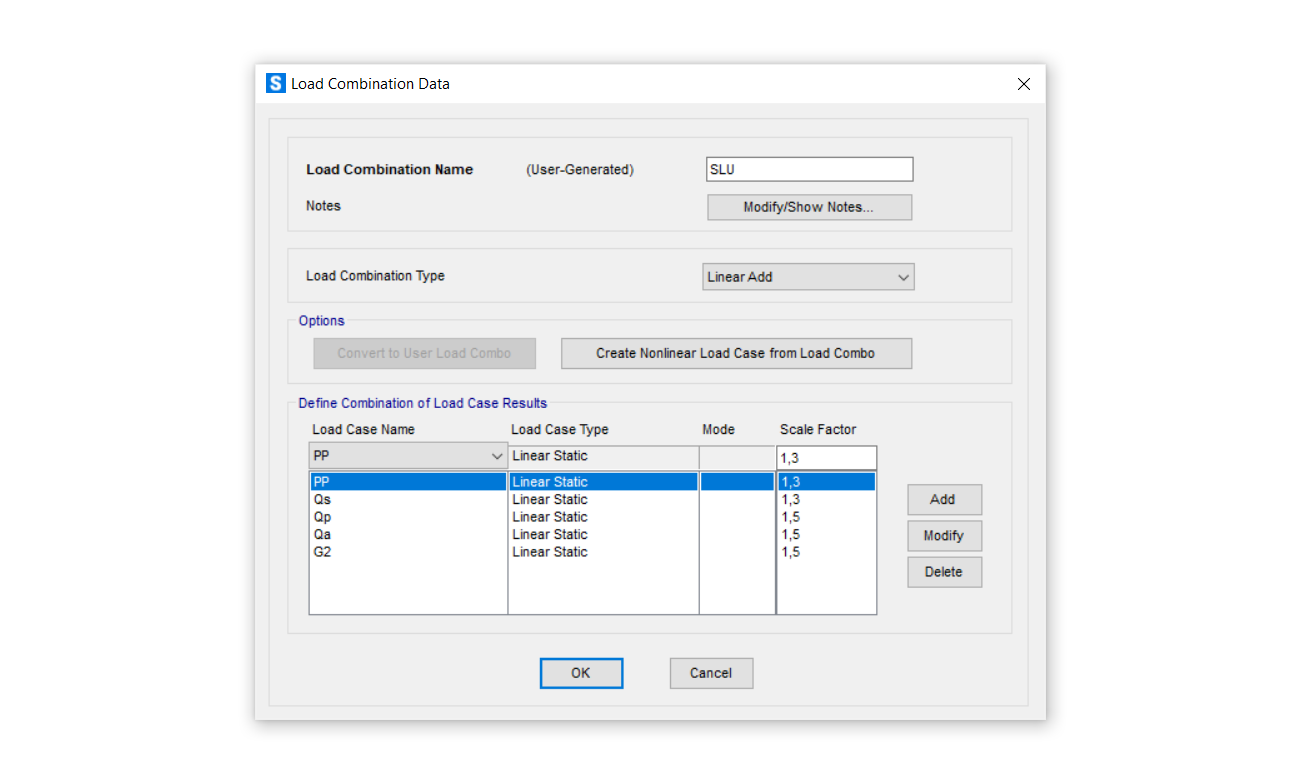
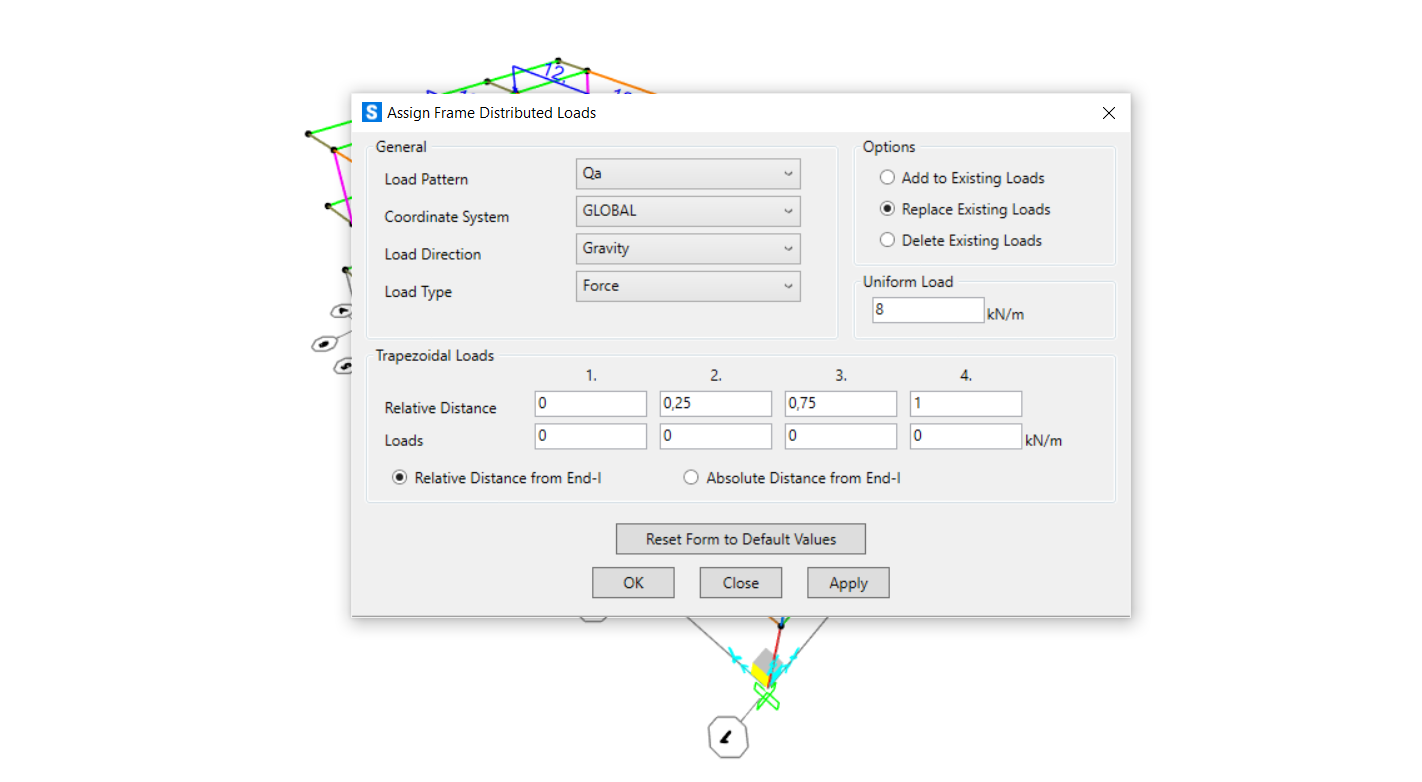
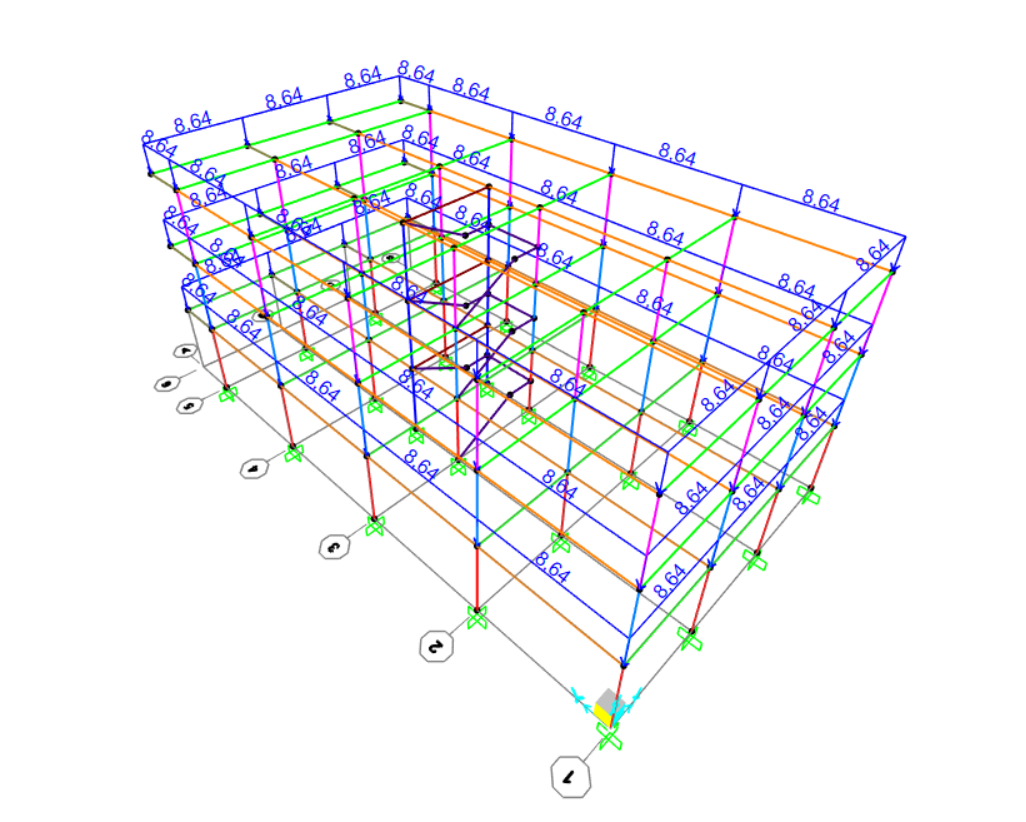Terminato il modello abbiamo avviato l'analisi e ottenuto così la configurazione deformata.

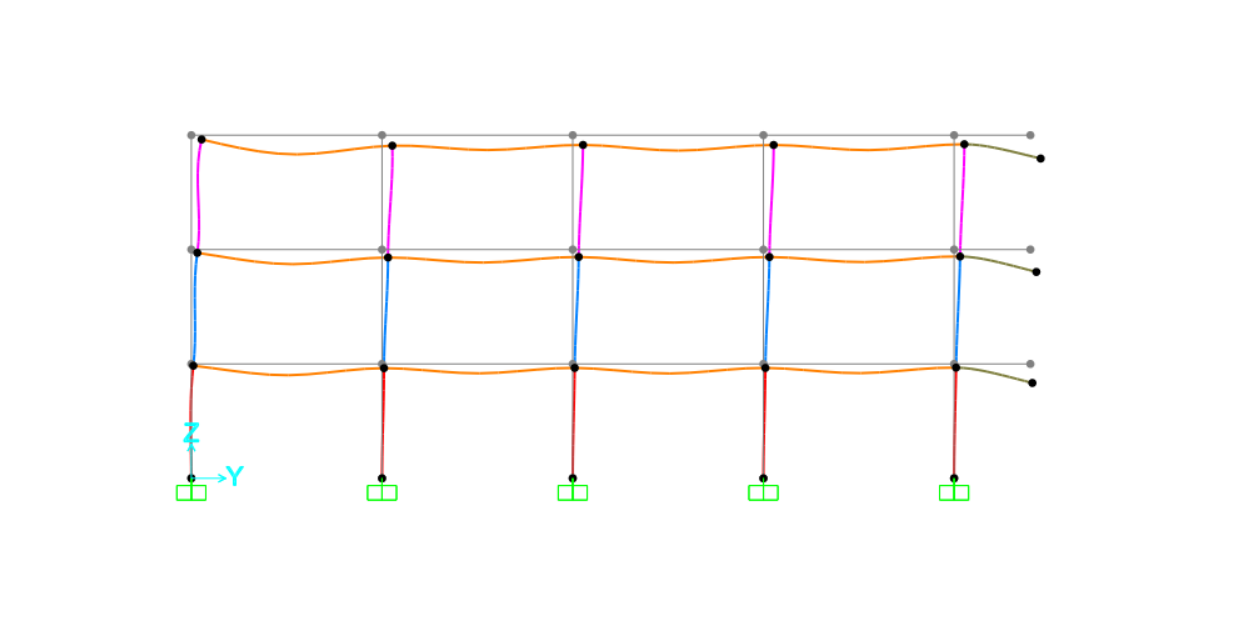
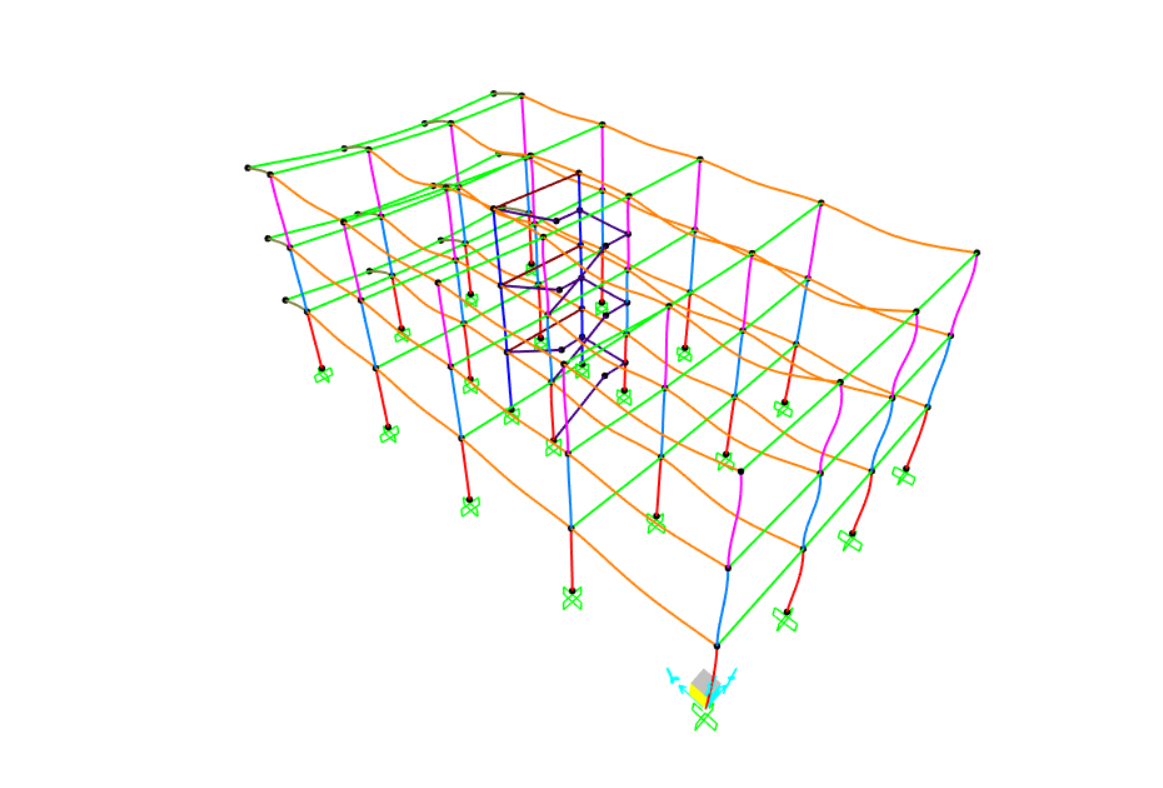DIAGRAMMA SFORZO NORMALE

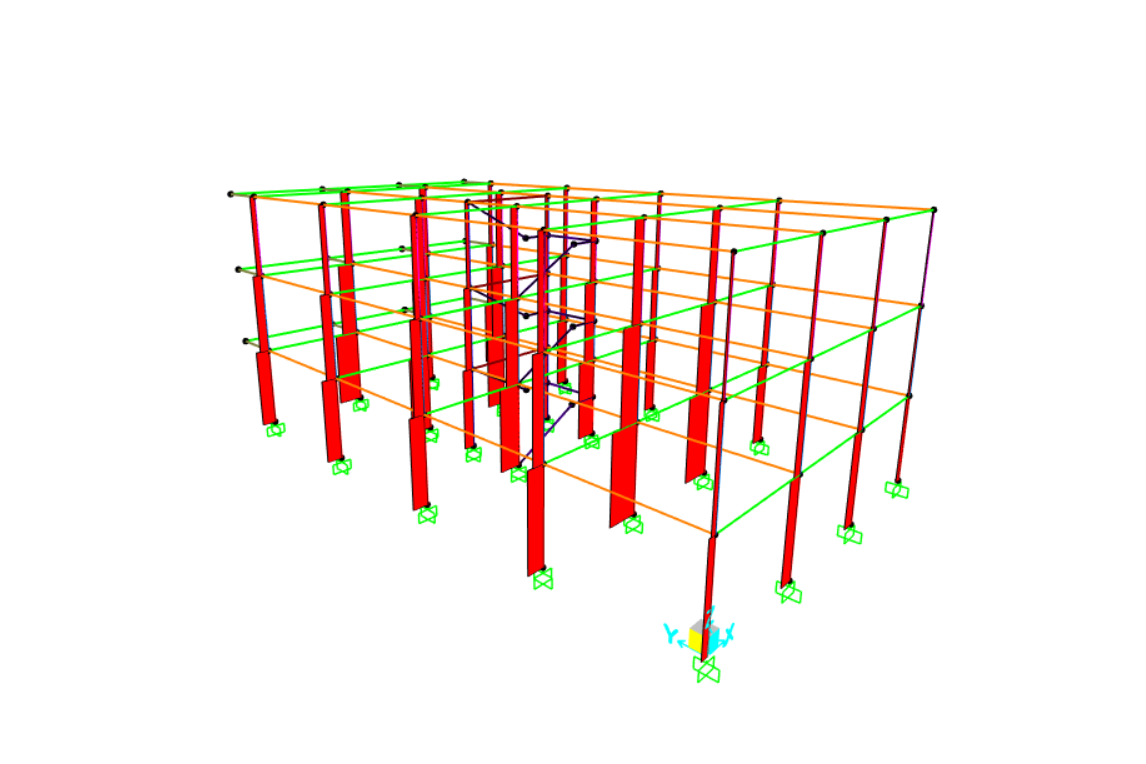DIAGRAMMA TAGLIO 2-2

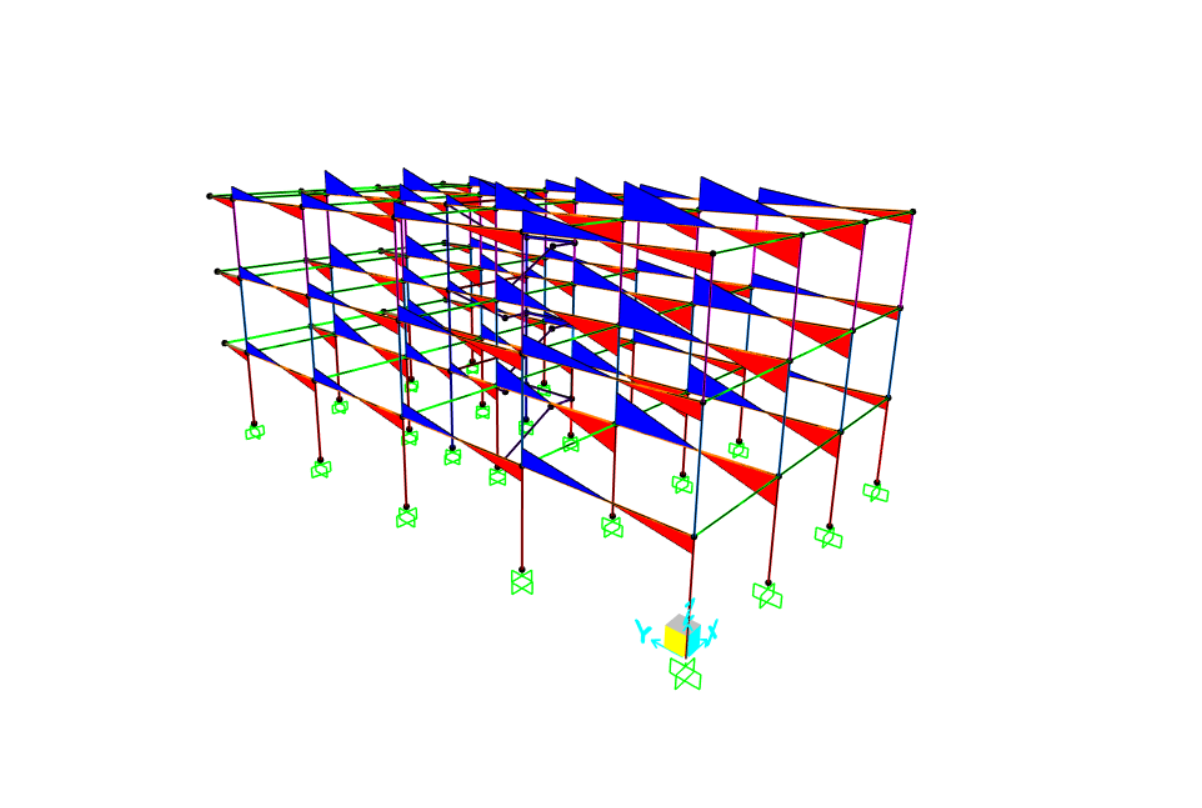DIAGRAMMA TAGLIO 3-3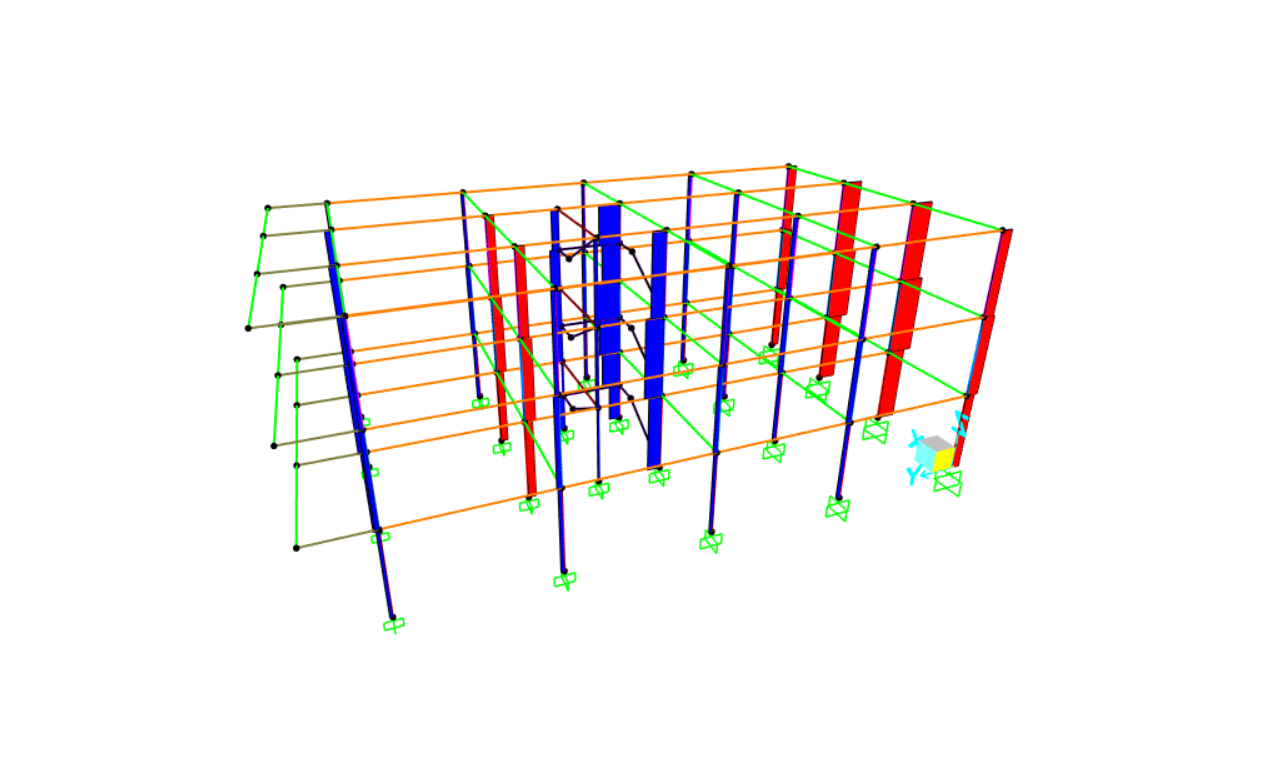DIAGRAMMA MOMENTO 2-2

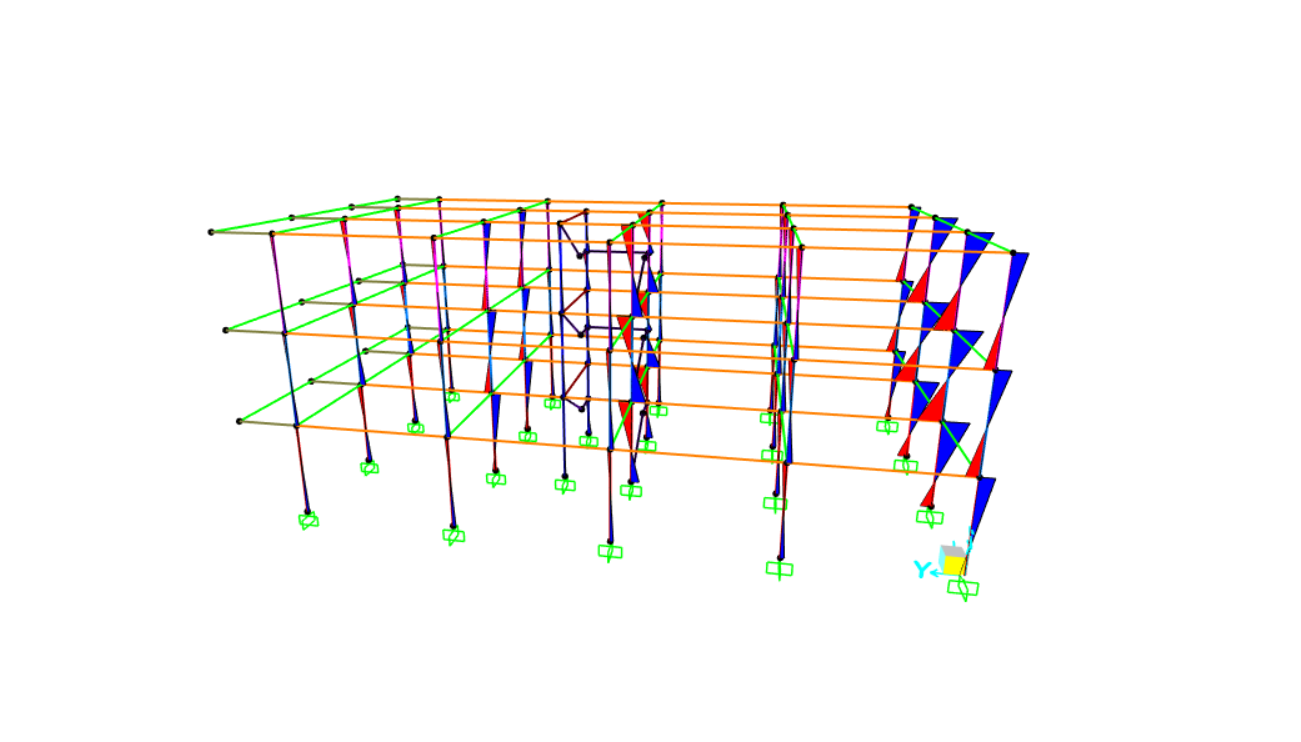DIAGRAMMA MOMENTO 3-3

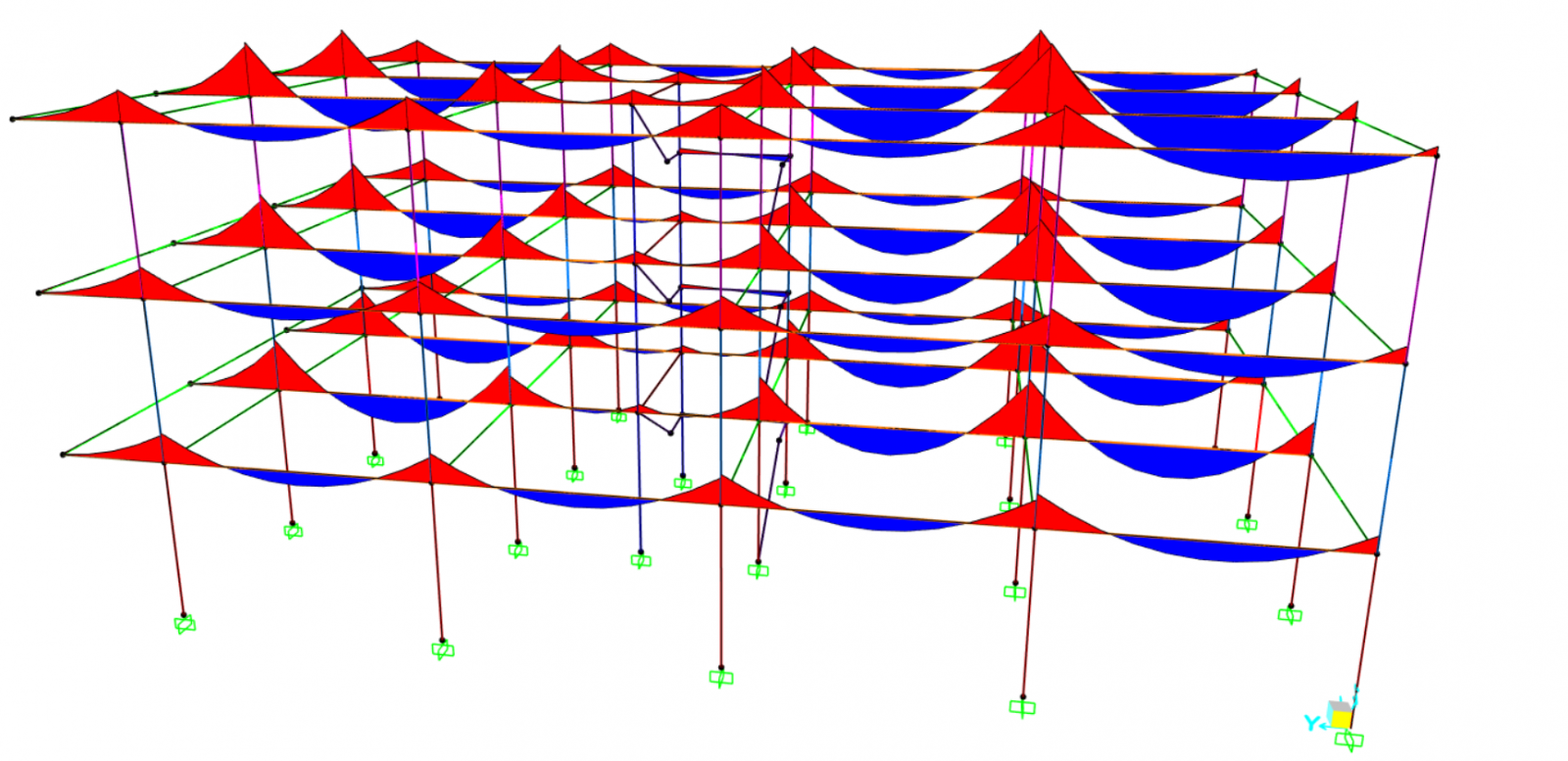
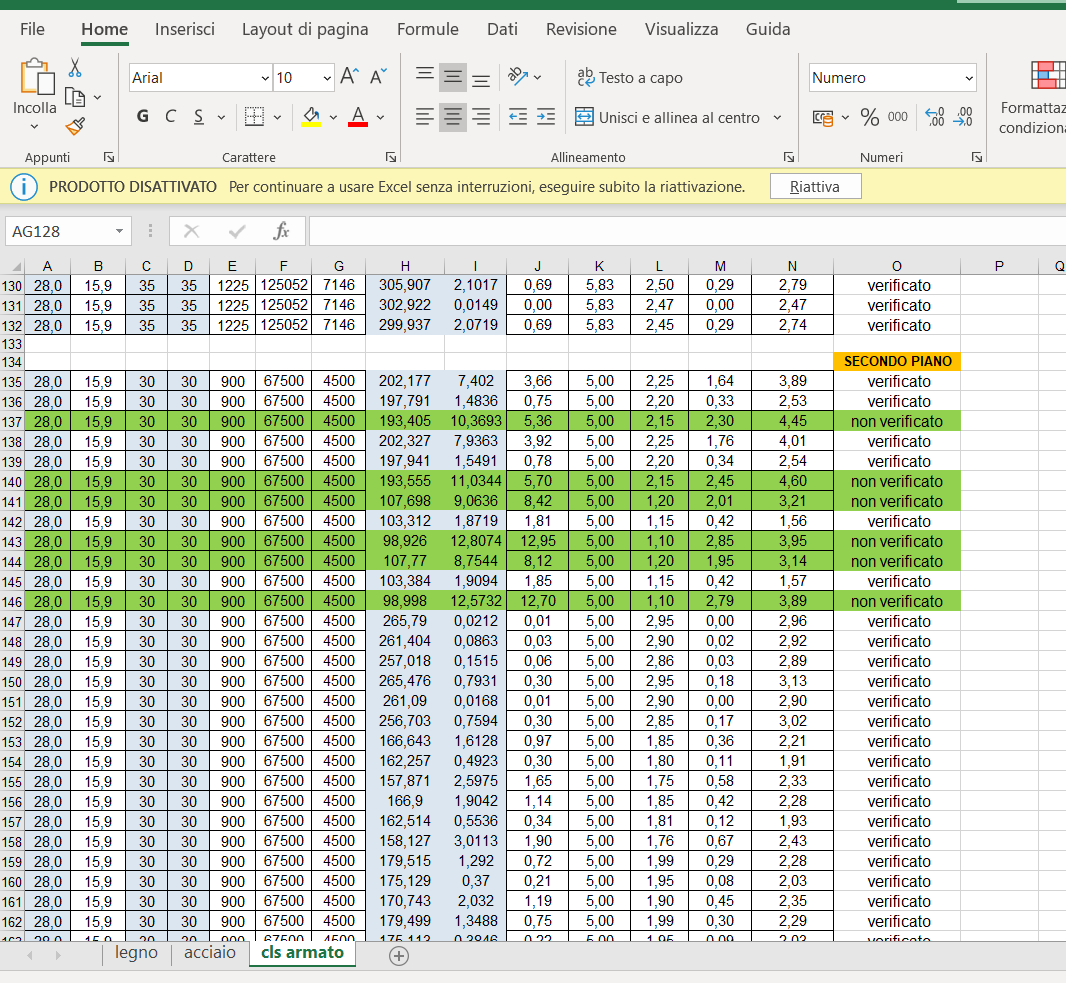
Abbiamo infine esportato le tabelle su Excel, divise in gruppi, e per ciascuno abbiamo preso gli sforzi massimi e verificato le sezioni.

VERIFICA

Terminata l'analisi è stata fatta la verifica degli elementi progettati sostituendo però le sollecitazioni di progetto con quelle ottenute da SAP2000. La verifica mette a confronto le tensioni agenti sulla sezione più sollecitata con le tensioni ammissibili: σmax ≤ fcd

Verifica travi a flessione

Per la trave la tensione massima è stata calcolata come rapporto tra momento massimo e modulo di resistenza a flessione massimo:  σmax= Mmax/Wmax    Mmax/Wmax≤ fcd

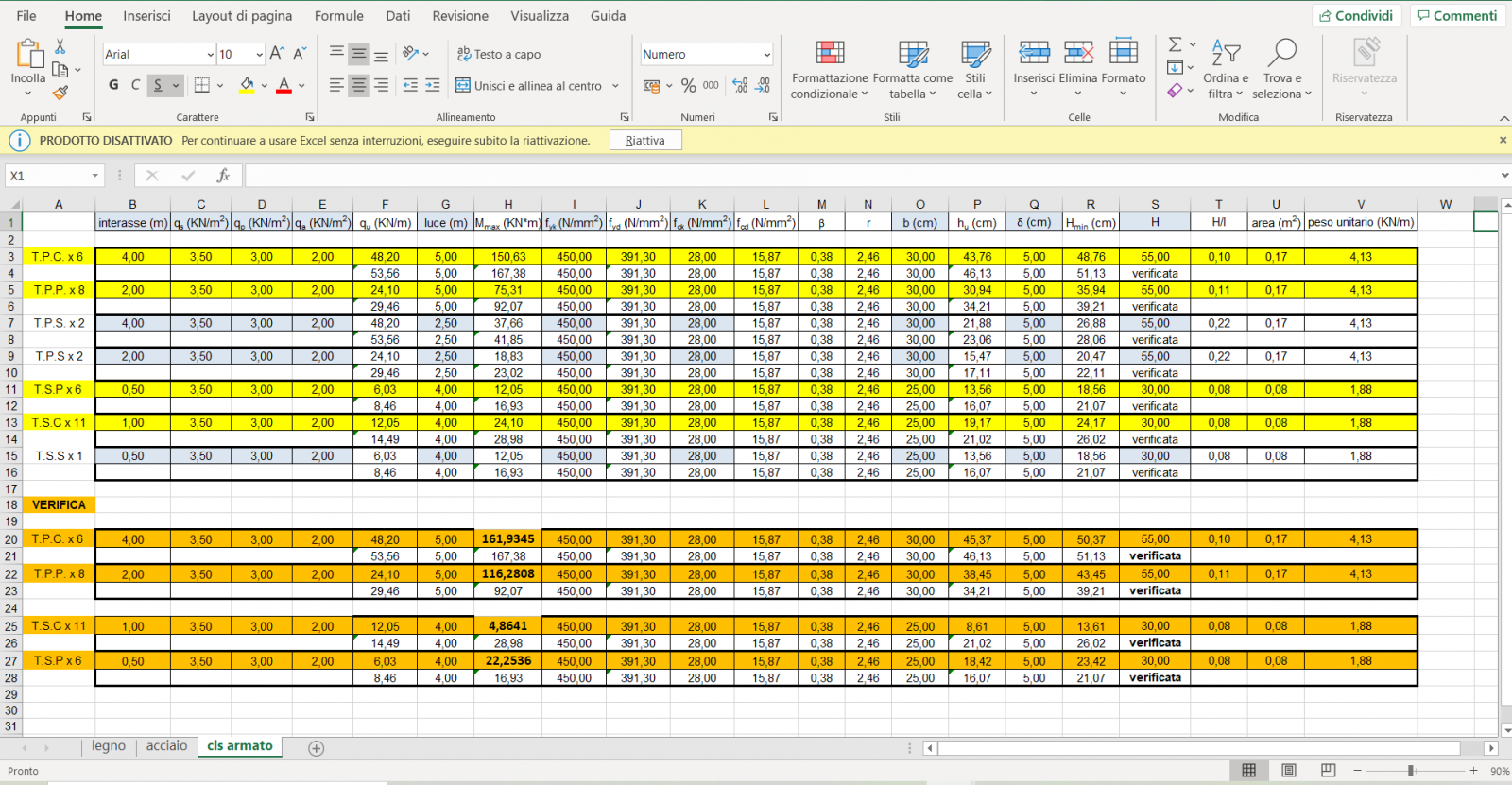
Verifica mensole

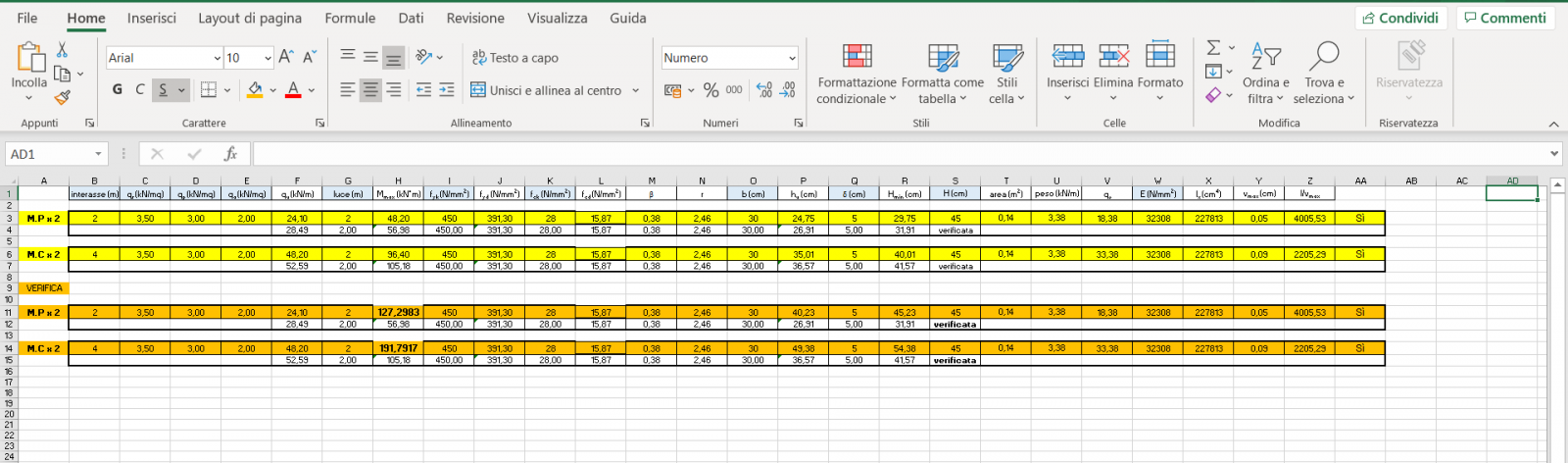
Verifica pilastri a pressoflessione

Per il pilastro la tensione massima è fornita dallo sforzo normale di compressione e dal momento flettente trasmesso dalla trave al pilastro: σmax= N/A+Mmax/Wmax
Da cui la verifica di una sezione presso inflessa: N/A+Mmax/Wmax≤ fcd.

In base ai valori di N e M ottenuti da SAP2000 abbiamo capito in quale tabella inserirci, ovvero se ci troviamo nel caso della piccola, moderata o grande eccentricità.

Al piano terra e al primo piano abbiamo riscontrato un'eccentricità piccola poiché i pilastri sono maggiormente soggetti a sforzo normale di compressione.

Al secondo piano abbiamo riscontrato alcuni pilastri con eccentricità moderata in quanto l'aumento dell'eccentricità è dovuto al decremento dello sforzo Normale che grava sui pilastri.