Esercitazione 3 - Patryk Rynkowski, Luca Santilli

Esercitazione 3: Dimensionamento di massima di un telaio in C.A. in zona sismica

Studenti: Patryk Rynkowski, Luca Santilli

Poiché nell’esercitazione precedente i pilastri a sezione quadrata risultavano non verificati, abbiamo iniziato sostituendo quest’ultimi con dei nuovi a sezione rettangolare di dimensioni:

• PT: 40x40 -> 55x35
• P1: 35x35 -> 50x30
• P2: 30x30 -> 45x25

Visualizziamo i valori dei nuovi pilastri sulla tabella Excel della scorsa esercitazione.

Autocad

Pianta P1:

Pianta controventi:

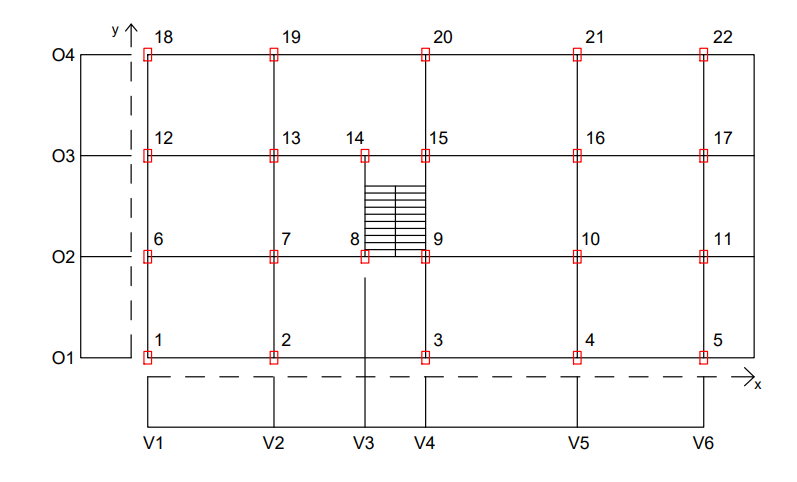
Prospetto:

Sezione corpo scala: 

Con i risultati ottenuti dal dimensionamento dei nuovi pilastri, calcoliamo le rigidezze traslanti dei controventi del nostro telaio e le inseriamo nella tabella:

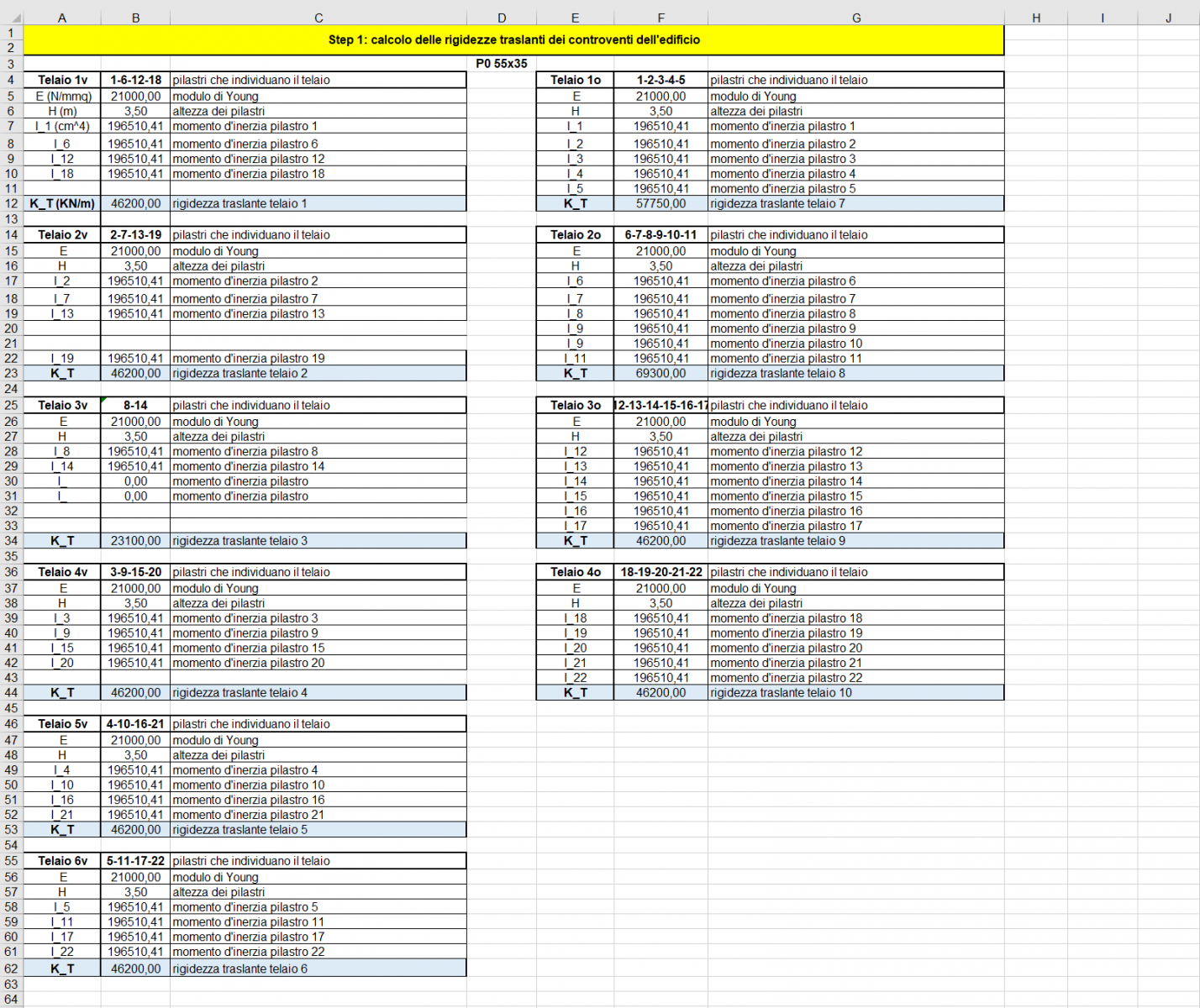
Nella successiva tabella inseriamo i valori della rigidezza di ogni controvento e le relative distanze:

Vediamo la rigidezza orizzontale, verticale e a torsione del telaio.

Individuiamo il centro di massa.

A questo punto torniamo su SAP e delineiamo il centro di massa grazie all’intersezione delle due diagonali.

(Medesimo procedimento sarà applicato ai piani superiori)

Tramite il comando Diaphram assegniamo la condizione di impalcato ai punti appena creati.

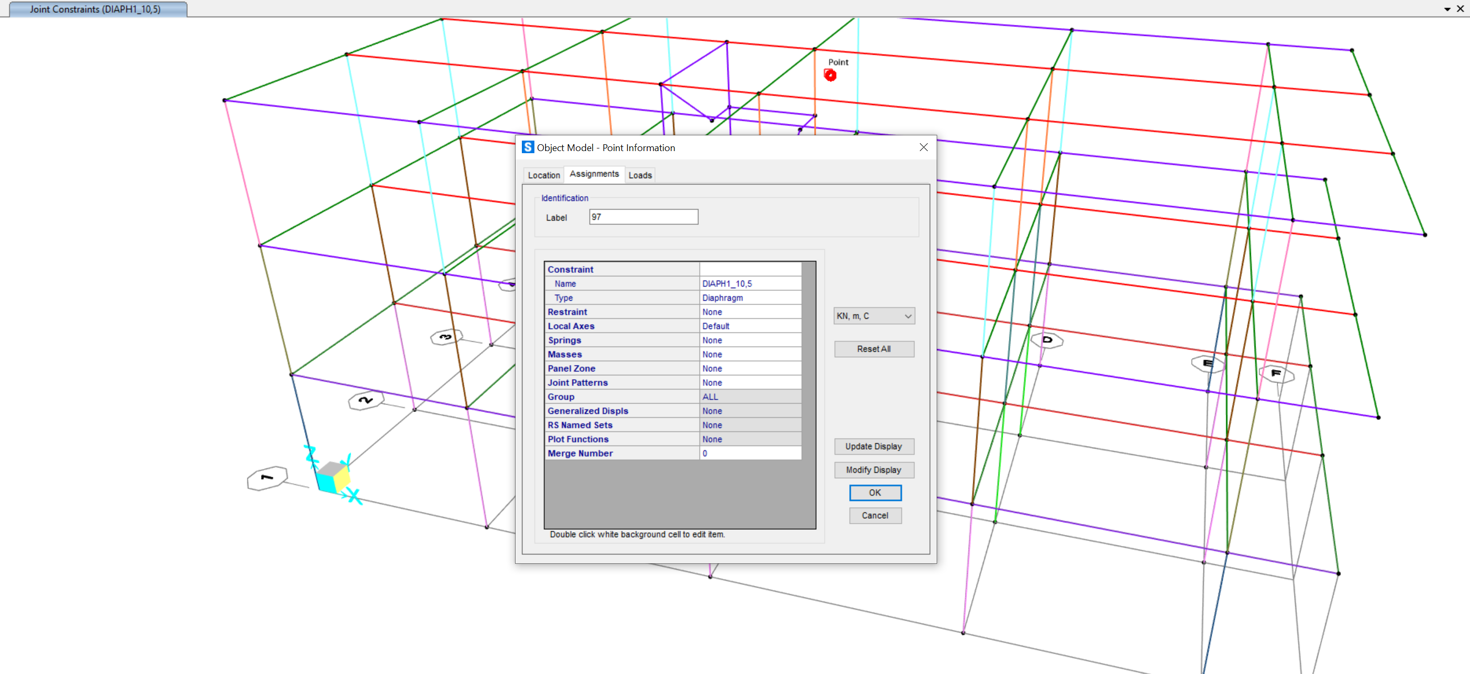
Passiamo a definire i casi di carico (Load Patterns) per le due direzioni dove agiranno le forze sismiche:

X e Y, Fx e Fy

Calcoliamo adesso la Forza Sismica orizzontale, ricavando i seguenti valori:

• qs=3,5
• qp=3
• qa=2

P = Qs+Qp+(y*Qa)

• Qs = A tot x npiani x qs 
• Qp = A tot x npiani x qp 
• Qa= A tot x npiani x qa 

P = 7558,27 kN

Fs= P x c = 7558,27 x 0,2 = 1511,65 kN (c=coefficiente di intensità sismica di Roma)

La forza sismica va distribuita per i 3 piani (h3,5m).

Fi = ( hi x Fs )/åhi

• FP1 = (1511,65 x 3,5) / 21 = 251,94 kN
• FP2 = (1511,65 x 7) / 21 = 502,88 kN
• FP3 = (1511,65 x 10,5) / 21 = 755,82 kN

Ora assegniamo le forze ricavate su X e Y per tutti i piani:

Fx:

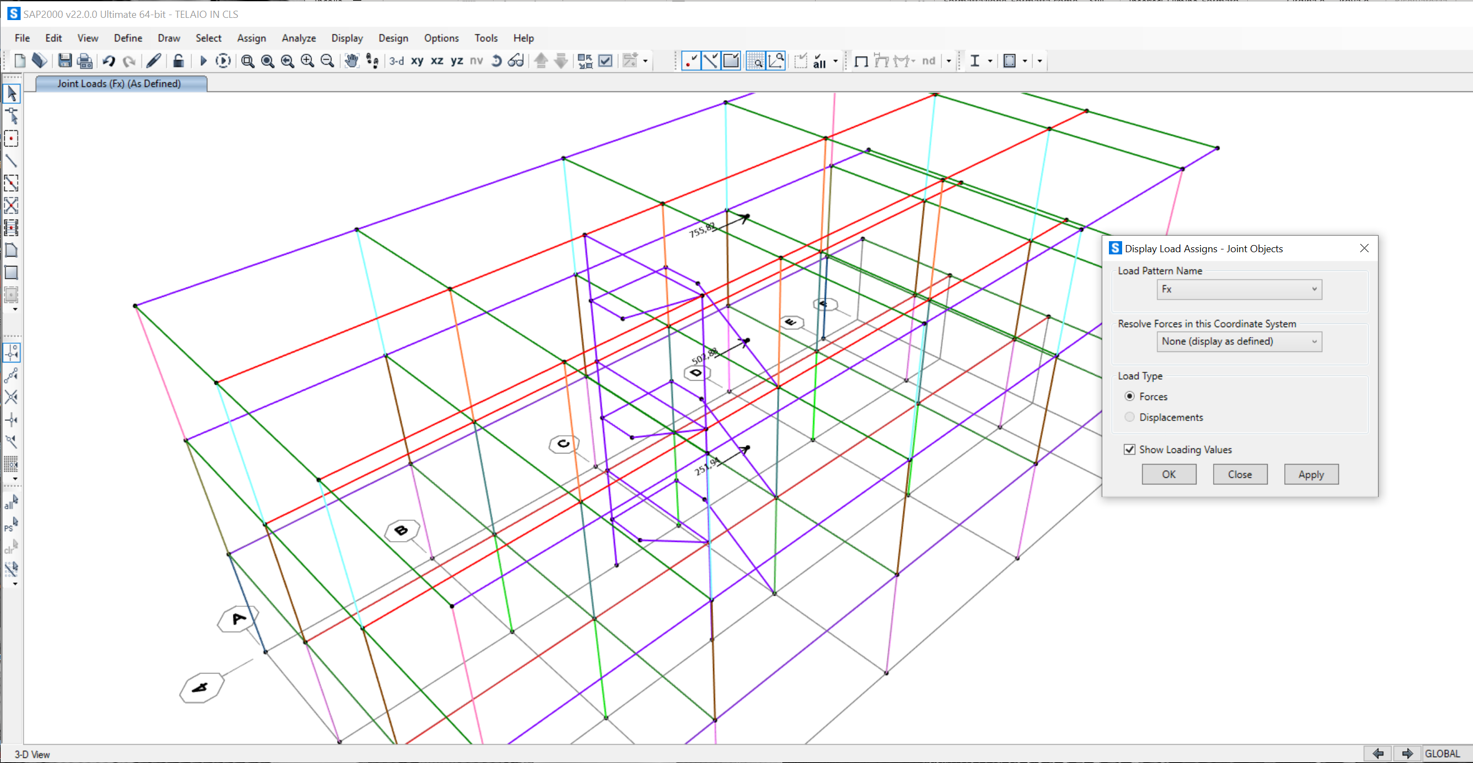
Fy:

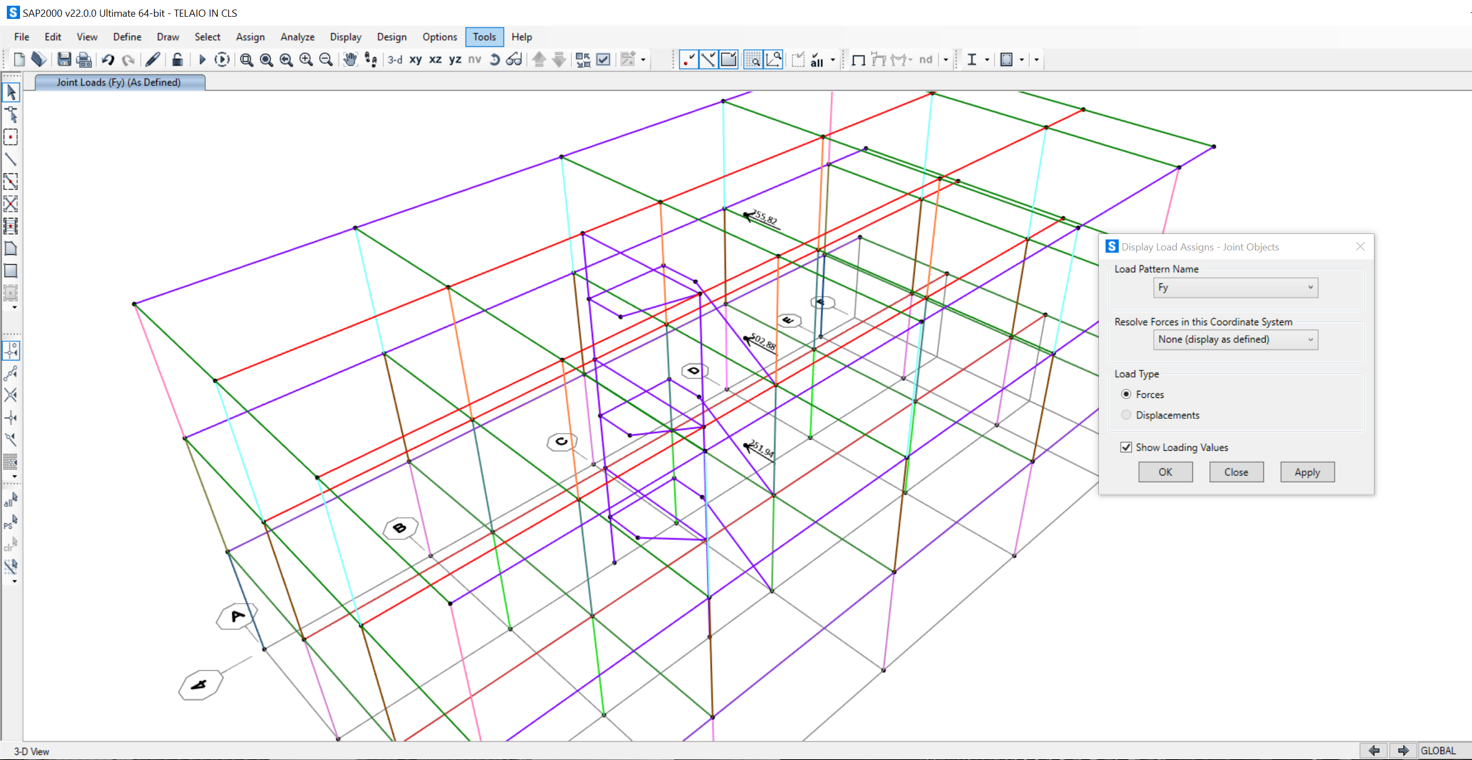
Visualizziamo i dati di ogni punto tramite il comando Point Information:

P1

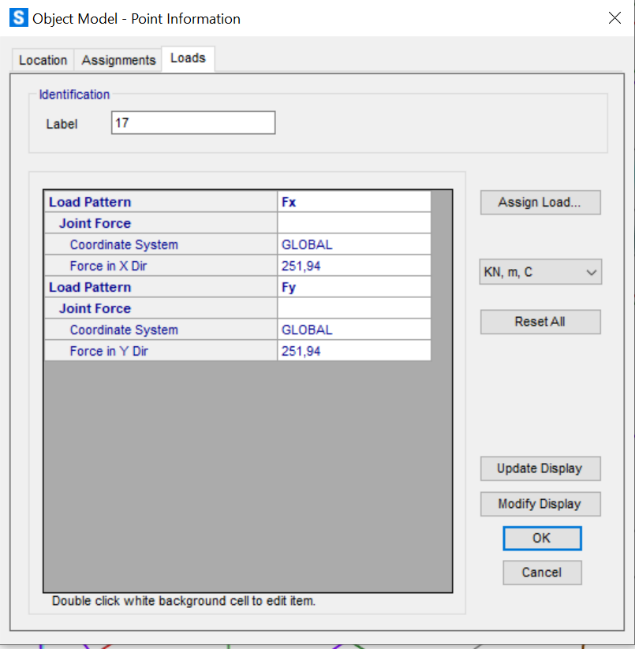
P2

P3

Avviamo una prima analisi che prenda in esame soltanto le deformazioni dovute allo sforzo sismico. 

Una seconda analisi prenderà invece in esame soltanto i carichi, senza considerare momentaneamente gli sforzi dovuti alla presenza della zona sismica.

Infine, avviamo l’analisi considerando tutti i carichi in zona sismica.

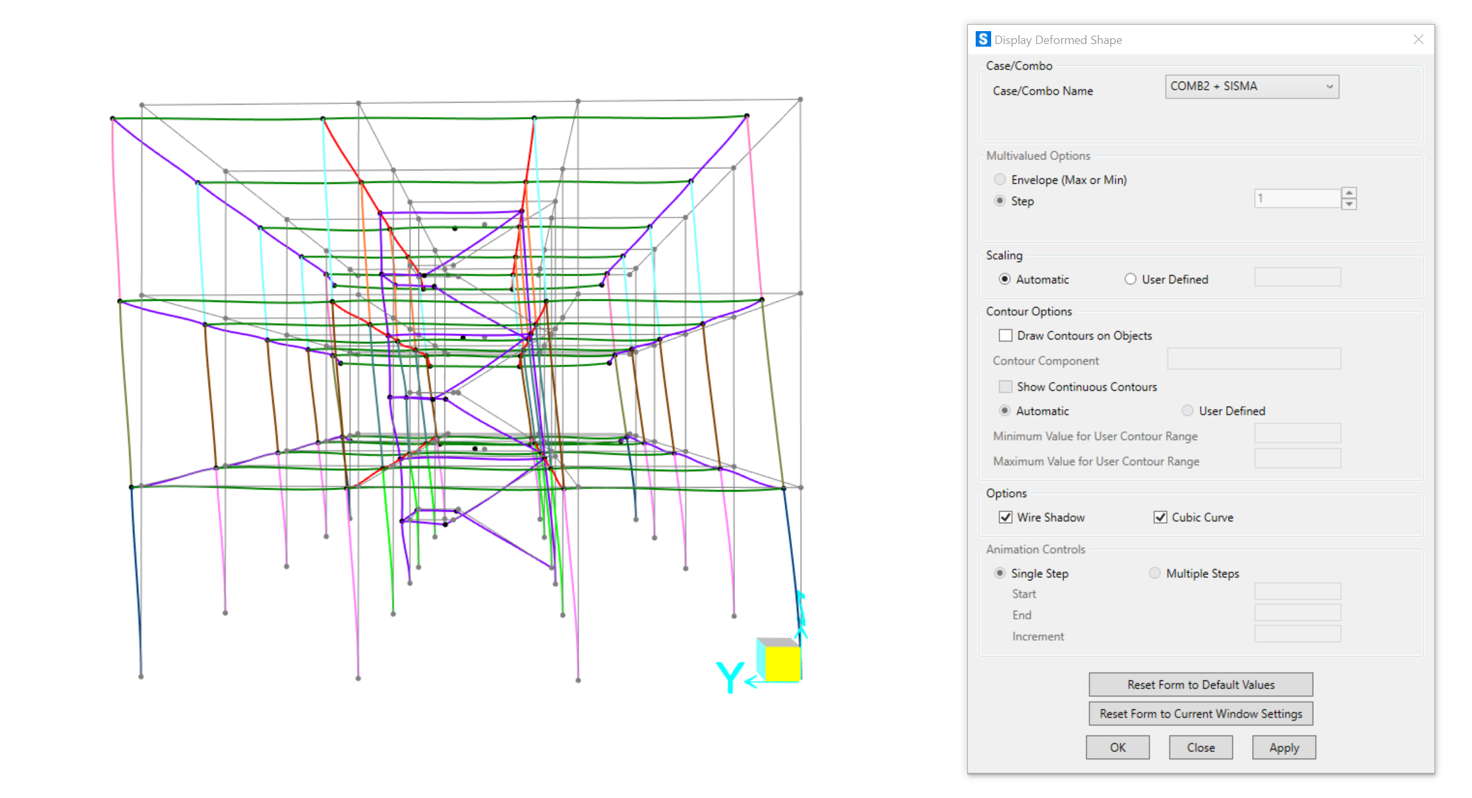
Visualizziamo la forza agente lungo l’asse x:

Gm = (12,00;6,00)Gc = (10,78;5,44)dc = -0,56m

Φ = (fx*dc/ko)     P1 -> -7,51*10^-5     P2 ->  -2,25*10^-5

Fo = Fx/Ko

P1 = 251,94 / 18771169,89 = 0,000013m

P3 = 755,82 / 18771169,89 = 0,000040m

 

Visualizziamo la forza agente lungo l’asse y:

Gm = (12,00;6,00)Gc = (10,78;5,44)dc = -1,22m

• = (fx*dc/ko)     P1 -> -1,64*10^-5        P3 -> -4,91*10^-5        

Fo = Fx/Ko =

P1 = 0,000013m

P3 = 0,000040m

Esportiamo i risultati dell’analisi relativi agli sforzi in direzione x sulla tabella Excel:

Tabella degli sforzi in direzione X (b55cmxh35cm)C28/35

FRAME 49

N = 3369,52 kNM3 = 199,46 kN

e = M:N = 0,06 -> 6cm 6>H/6

MODERATA ECCENTRICITÀ   h/6(5,8)<e <h/2(17,5)     

(Prima piccola eccentricità)

I = b*h³/12 = 196510,4cm⁴

Wx = b*h²/6 = 11229,16cm³

Fcd = 15,9 Mpa

U = h/2-e à 35/2 – 6 = 11,5

Σmax = (2*N*1000)/3*u*b*100 = 35,51 Mpa < fcdNON VERIFICATO

(dovremmo scegliere una sezione maggiore)

Vediamo i diagrammi su SAP.

Forza sismica in X:

Totale in X:

Esportiamo i risultati dell’analisi relativi agli sforzi in direzione y sulla tabella Excel:

Tabella degli sforzi in direzione X (b55cmxh35cm)C28/35

FRAME 49

N = 3830,11 kNM2 = 60,16 kN

e = M:N = 0,015 -> 1cme>H/6(PICCOLA ECCENTRICITÀ, come prima)

I = 196510,4 cm⁴

Wx = 11229,16 cm³

U = h/2 – e à 16,5

Fcd = 15,9 Mpa

σmax = 2*N*1000/3*u*b*100 = 28Mpa>fcd   NON VERIFICATO

Vediamo i diagrammi su SAP.

Forza sismica in Y:

Totale in Y:

Render: