Esercitazione 2: Dimensionamento struttura a telaio in C.A.

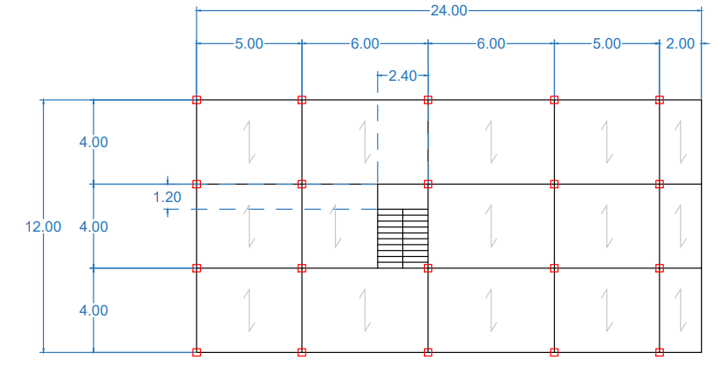
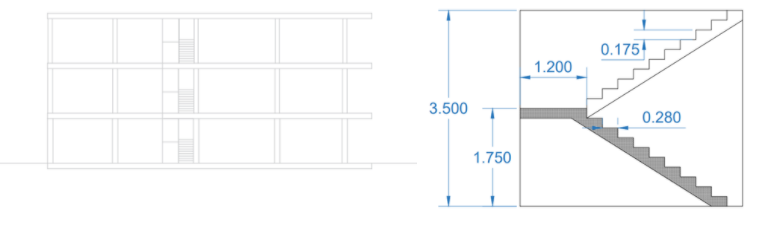
Iniziamo con il disegno su Autocad della pianta del solaio del caso di progetto, con le seguenti dimensioni: 24m lungo l’asse x, 12m lungo l’asse y, 3,5m lungo l’asse z (altezza interpiano), con 3 piani totali. Il corpo scala misura 4mx2,4m, con un’alzata di 17,5cm, una pedata di 28cm e il pianerottolo 1,2mx2,4m. Lo sbalzo lungo l’asse x misura 2m.
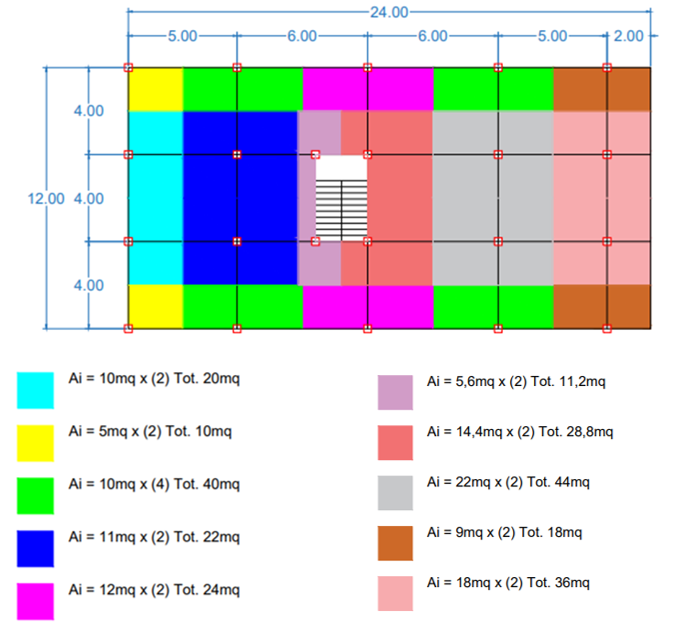
Ora raggruppiamo le aree d’influenza Ai dei pilastri e le calcoliamo.
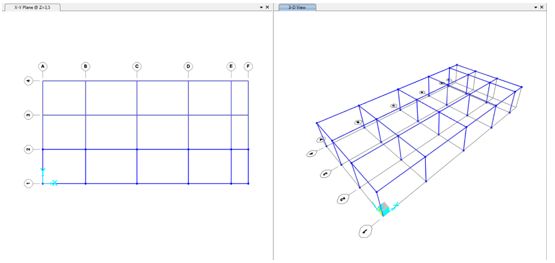
Passiamo su SAP2000 e procediamo al ridisegno della struttura.
A questo punto iniziamo con il pre-dimensionamento della trave principale, scegliendo innanzitutto il materiale da SAP C28/35.
Dal foglio Excel abbiamo modificato l’interasse e la luce e Fck (28). Mettendo come base b 30cm, come altezza h 55cm, la sezione è verificata.
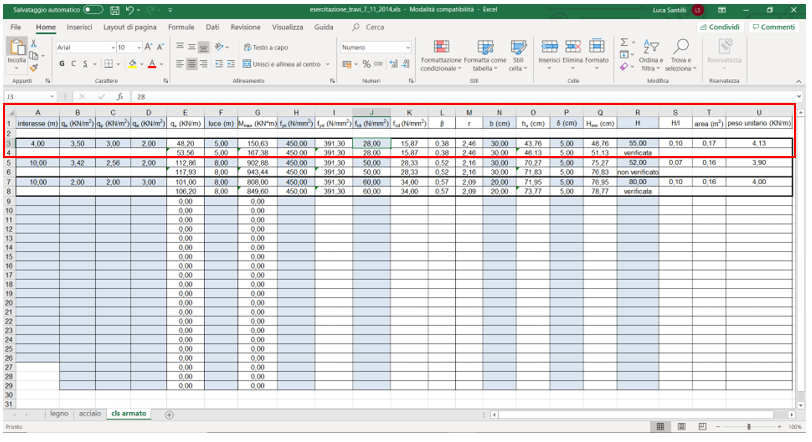
Su SAP, aggiungiamo una nuova sezione chiamata TRAVE PRINCIPALE (rosso), con il materiale scelto C28/35 e gli riportiamo le dimensioni ottenute dal foglio Excel (h0,55 b0,3).
Tornando al foglio Excel passiamo alla seconda trave, modificando l’interasse e la luce e Fck(28). Scegliendo come base b25 cm, come altezza h 35cm, la sezione risulta verificata.
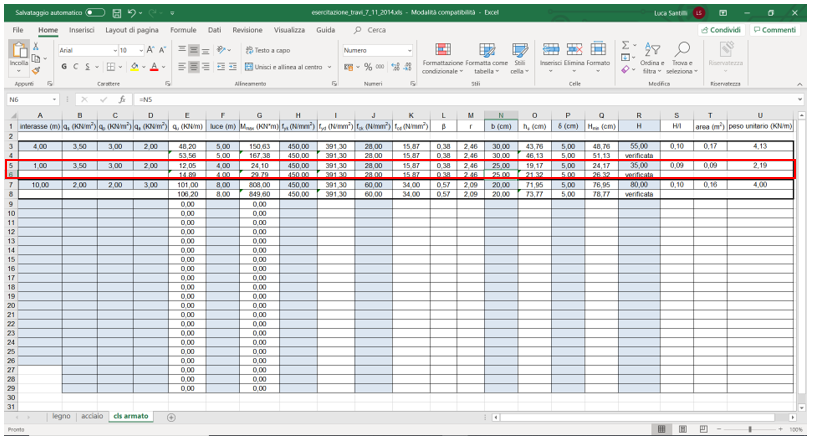
Su SAP, definiamo una nuova sezione chiamata TRAVE SECONDARIA (arancione), con il materiale scelto C28/35 e gli riportiamo le dimensioni ottenute dal foglio excel (h0,35 b0,25).
Passiamo al dimensionamento delle mensole tramite il foglio Excel, qui modifichiamo i valori base b 30cm e altezza h 50cm, così la sezione risulta verificata.
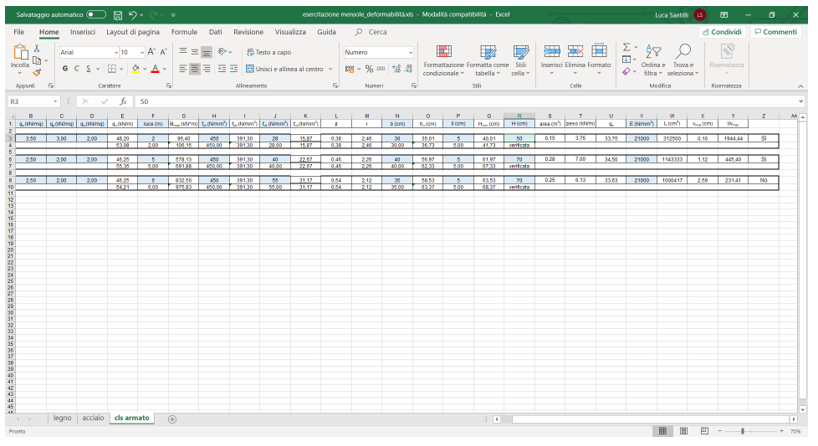
Definiamo una nuova sezione su SAP chiamata MENSOLA(verde) dello stesso materiale C28/35 ma con altezza h 50cm e base b 30cm, così da foglio Excel.
Ora dobbiamo definire il peso delle travi principali e secondarie che poggiano sul pilastro. Su SAP utilizziamo i comandi: DEFINE-SECTION PROPERTIES-SHOW MATERIALS, da lì vediamo il peso per unità di volume (25).
Sul foglio excel, nel peso della trave principale facciamo l’operazione =25*0,3*0,55 e otteniamo il peso in kN/m 4,13. Ripetiamo l’operazione per la trave secondaria e otteniamo il peso in kN/m 2,19. Copiamo la fila per il numero dei piani (3). Aggiungiamo il modulo elastico E alla tabella (32308 Mpa).
Abbiamo definito la sezione dei tre pilastri dei vari piani:
- (PT=40cmx40cm)
- (P1=35cmx35cm)
- (P2=30cmx30cm)
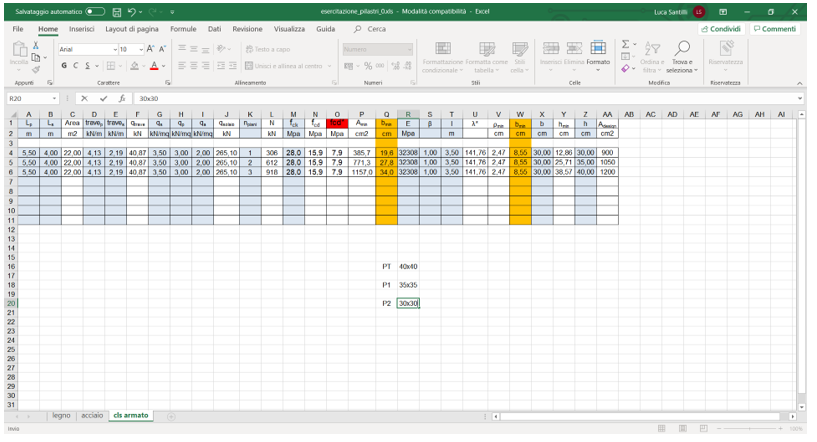
Su SAP, definiamo i pilastri.
Definiamo travi principali centrali(TP_C), principali perimetrali (TP_P), secondarie (TS).
Aggiungiamo nuove sezioni per il corpo scala: cordolo (SCALA_CORDOLO: cyano), ginocchio (SCALA_GINOCCHIO: rosa antico), montanti (SCALA_MONTANTI: rosso vino).
Disegniamo dalla vista 3d il corpo scale, e creiamo un unico gruppo che contenga tutti gli altri (SCALE: viola). Assegniamo le sezioni alle travi principali, secondarie, mensole e pilastri. Separiamo la trave principale nel punto di congiunzione con il cordolo della scala.
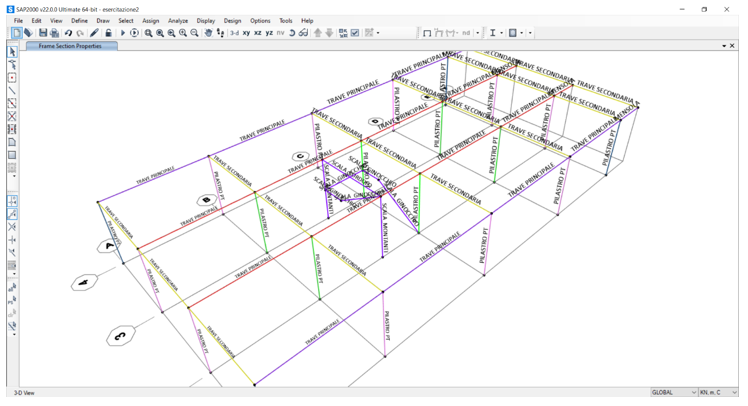
Una volta copiato il modello e aver creato i piani superiori ci mettiamo in vista 3d x-y con apertura 0 e assegniamo i frame dei piani 1-2 ai gruppi che abbiamo creato per il piano terra.
Ora definiamo i vincoli, assegnando un incastro per ogni pilastro a terra.
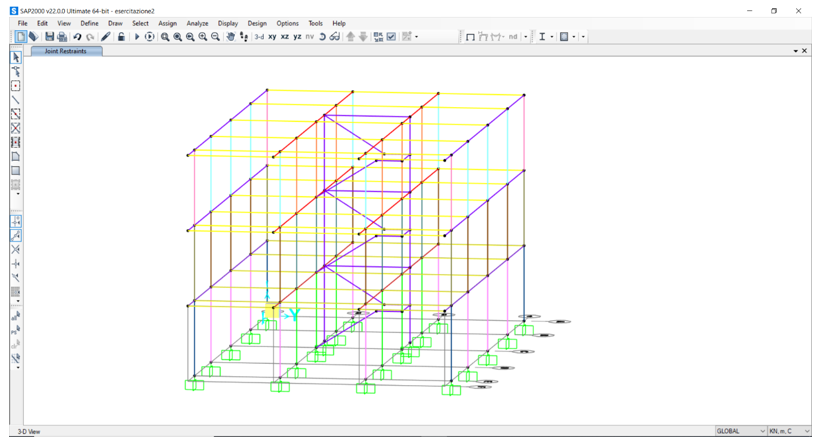
Selezioniamo tutte le travi di ogni piano attraverso la 2d view con z ad altezza di ogni rispettivo piano 3,5-7-10,5 e gli assegniamo la condizione di impalcato tramite il comando Diaphram.
Passiamo a definire i casi di carico creando i seguenti load patterns: Qa (moltiplicatore di peso proprio 0), Qp (moltiplicatore di peso proprio 0), Qs (moltiplicatore di peso proprio 0), PP (moltiplicatore di peso proprio 1).
Si definisce poi un load combination con tutti questi carichi, ognuno moltiplicato per il proprio coefficiente maggiorativo da normativa:
- PP: Scale factor = 1,3
- Qs: Scale factor = 1,3
- Qp: Scale factor = 1,5
- Qa: Scale factor = 1,5
Consideriamo ora i carichi di tamponatura: tramezzi, muri pieni, muri con finestre e muri con porte e finestre.
Consideriamo il carico sulla scala: gradini e pianerottolo.
Inoltre, a tutto ciò va aggiunto il peso variabile.
Moltiplichiamo i carichi Qp, Qs, Qa per l’interasse:
Qs*I 3,5x2 = 7 kN/m
Qp*I 3,0x2 = 6 kN/m
Qa*I 2,0x2 = 4 kN/m
Qu = 12,05 kN/m
Calcoliamo il carico sulle travi principali perimetrali
Qtpp = 39,35 Kn/m Qtpc (senza scala) = 52,2 Kn/m Qtpc (con scala) = 26,1 kN/m
Calcoliamo il carico sulle travi secondarie perimetrali
Qtspm = 14,02 kN/m Qtspb = 15,62 kN/m
Trave secondaria balcone 5,25x0,5 = 2,6 kN/m
Trave secondaria centrale (senza scale) Qtsc 9,5 kN/m
Trave secondaria centrale (con scale) Qtsc 6,52 kN/m
Trave principale perimetrale (mensola) Qtpcpm 5,25 kN/m*2 = 10,5 kN/m
Trave principale centrale (mensola) Qtpcm 5,25 kN/m*4 = 21 kN/m
Calcoliamo la trave a ginocchio: Pianerottolo-trave 6 kN/m Qtgp = 8,16 kN/m Qg = 9 kN/m
A questo punto creiamo i load patterns con i carichi distinti per travi principali (con e senza scala), perimetrali e centrali secondarie (con e senza scala), mensola con balcone. Specifichiamo i carichi con finestre o muro pieno. Q per la scala sul pianerottolo e la trave a ginocchio.
PP*1,3
Qs*1,3
Qp*1,5
Qp*1,5
CARICHI:
- Tramezzi = 1kN/m²
- Muro = 10kN/m²
- Finestre = 8kN/m²
- Muro con porte e finestre = 7kN/m²
- Gradini = 2,5kN/m²
- Pianerottolo = 5kN/m²
- Peso variabile = 1,8kN/m²
NOTA: la moltiplicazione per il coefficiente di sicurezza (SCALE FACTOR) è stata fatta preventivamente, successivamente è stato moltiplicato il peso proprio PP con il coefficiente di sicurezza nella LOAD COMBINATIONS.
Assegniamo i carichi creati (DISTRIBUTED LOADS)
(NEL FILE PDF SI TROVANO GLI SCREENSHOT APPROFONDITI PER OGNI CASO DI CARICO)
Su Autocad disegniamo le piante indicanti i carichi con le rispettive Aree d’influenza Ai delle travi.
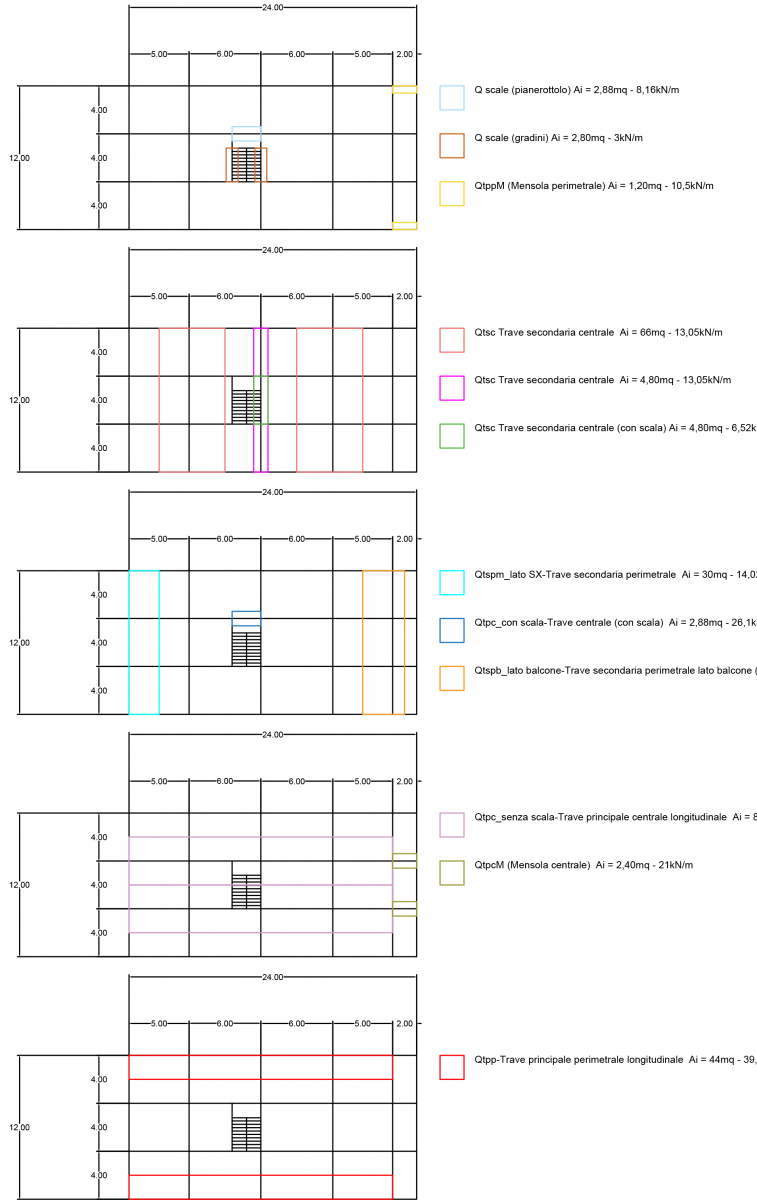
A questo punto possiamo avviare l’analisi.
Visualizziamo la struttura deformata tramite il comando SHOW DEFORMED SHAPE.
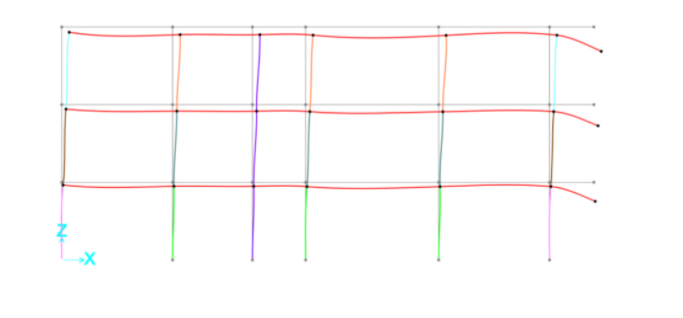
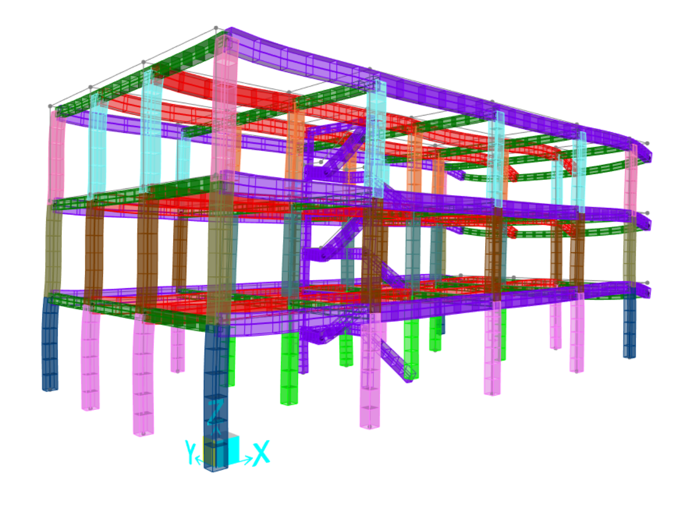
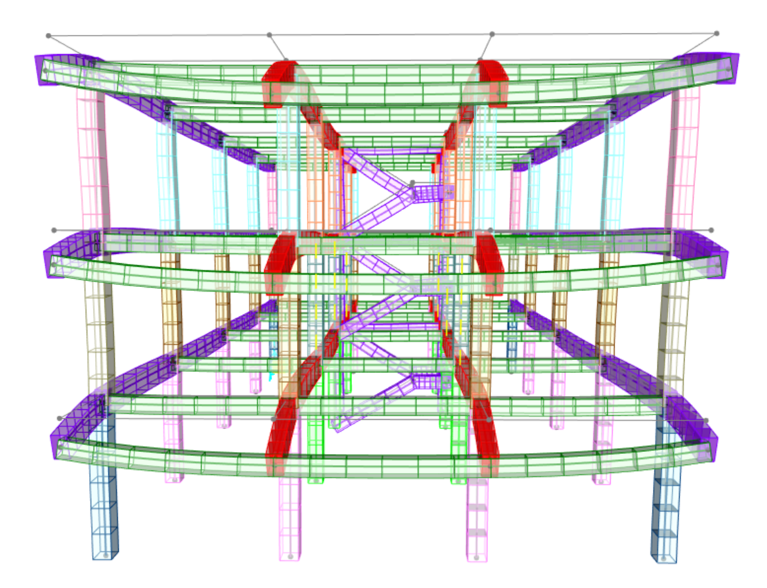
Ora, tramite il comando SHOW FORCES/STRESSES-FRAMES/CABLES/TENDONS, visualizziamo i diagrammi del momento in XZ.
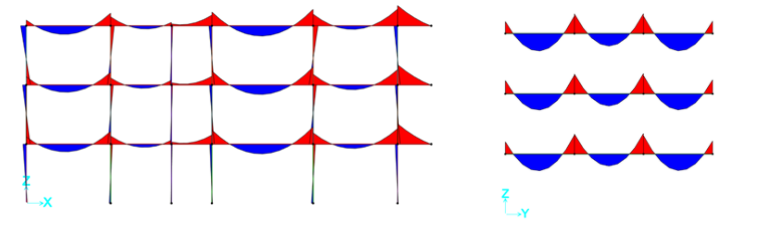
Ora il diagramma dello sforzo assiale dei pilastri.
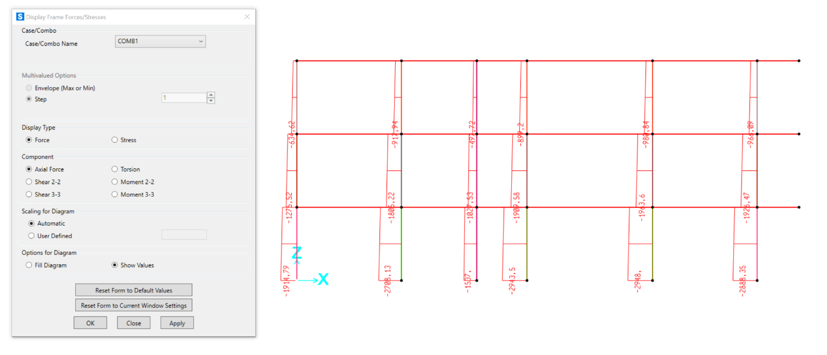
Ora mettiamo in evidenza i diagrammi del momento 33 con i relativi valori scaturiti dall’analisi.
Vista XZ:
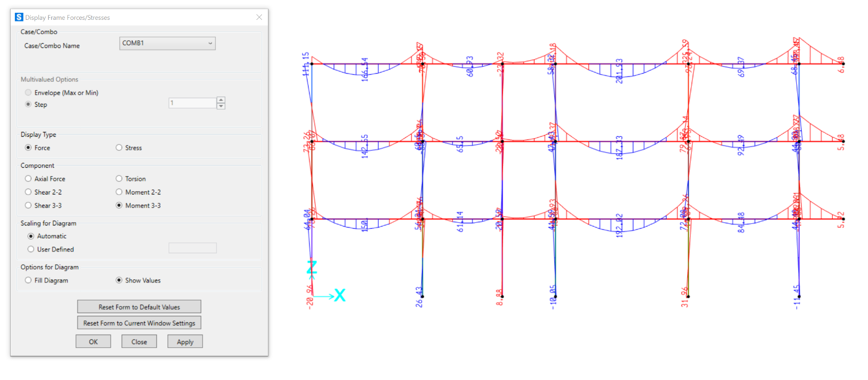
YZ:
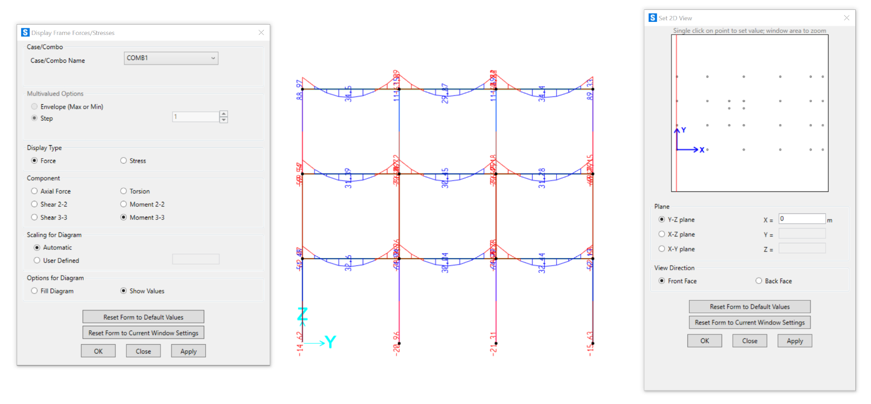
Infine, posizioniamo la vista trasversale dal lato opposto inserendo 24m come valore sull’asse X, affinché si vedano i diagrammi della facciata con gli sbalzi.
YZ:
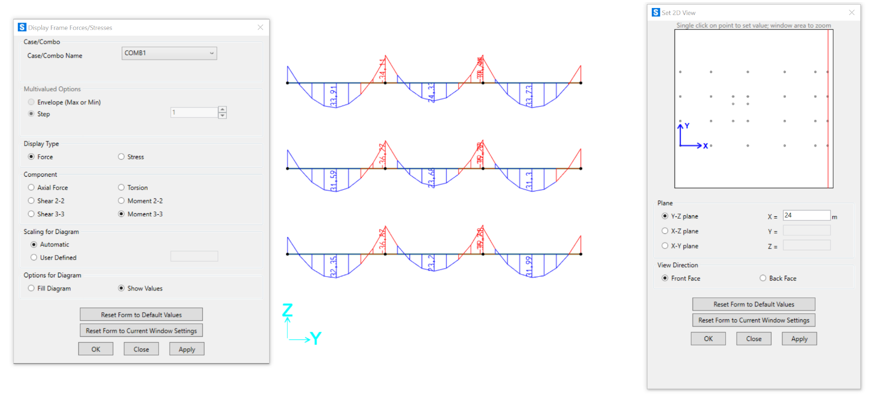
Per visualizzare le tabelle: Display – Show Tables, scegliamo i casi di carico con Select Load Patterns e spuntiamo ANALYSIS RESULTS.
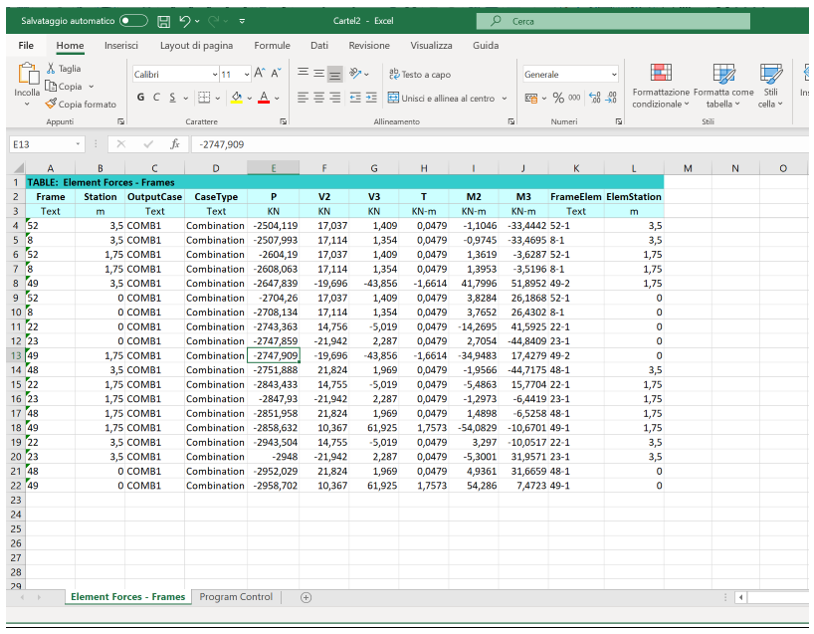
Nella tabella che si apre scegliamo Elements Forces/Frames, valori che saranno utilizzati per il successivo dimensionamento.
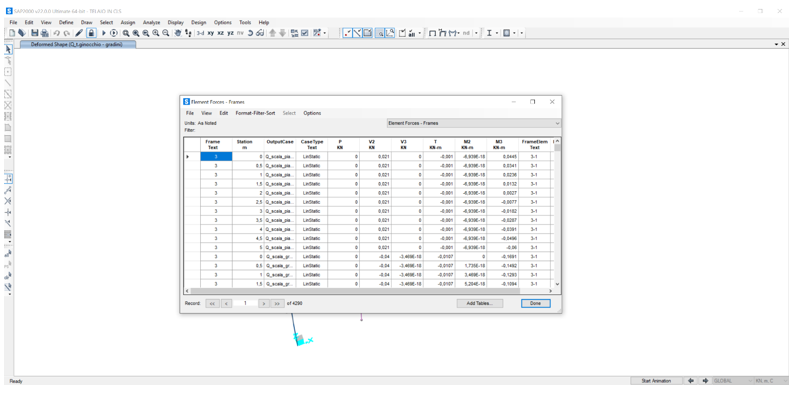
Esportiamo questa tabella su Excel e ne ricaviamo i valori del momento M3 per le travi:
TRAVI
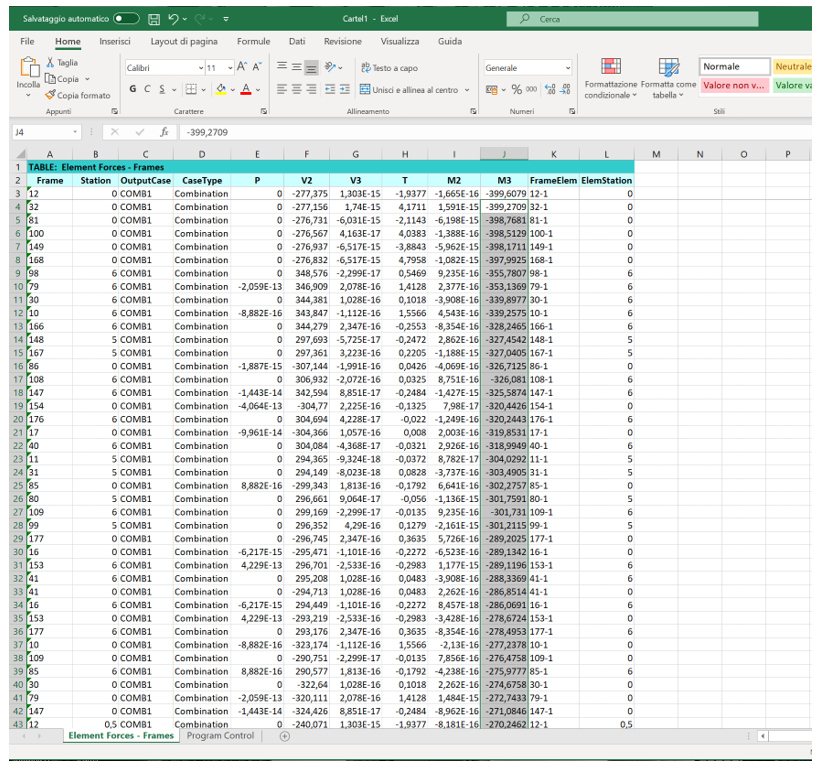
TRAVI PRINCIPALI CENTRALI (h55,b30)
- M Max = 204,3 kN/m à 204300 Nm
- Hu = r*rad (H:b) = 2,46xrad(6810) = 0,62xrad(6810) = 51
- H = 56 > 55 NON VERIFICATA
Scegliamo quindi travi 60x30 à OK
TRAVI PRINCIPALI PERIMETRALI (h55,b30)
- M Max = 158,6 kN/m à 158600 Nm
- Hu = 0,62xrad(158600:30) à 45
- H = 50 VERIFICATA
MENSOLE CENTRALI (h50,b30)
- M Max = 399,6 kN/m à 399600 Nm
- Hu = 0,62xradq(399600:30) = 71,5
- H = Hu + δ = 76,5 NON VERIFICATA
Scegliamo quindi 80x30 à OK
MENSOLE PERIMETRALI (h50,b30)
- M Max = 254,6 kN/m à 254600 Nm
- Hu = 57,11
- H = 62 NON VERIFICATA
Scegliamo quindi 65x30 à OK
TRAVI SECONDARIE (h35,b25)
- M Max = 36,9 kN/m à 36900 Nm
- Hu = 23,81
- H = 28,81 VERIFICATA
Visualizziamo i diagrammi su SAP:
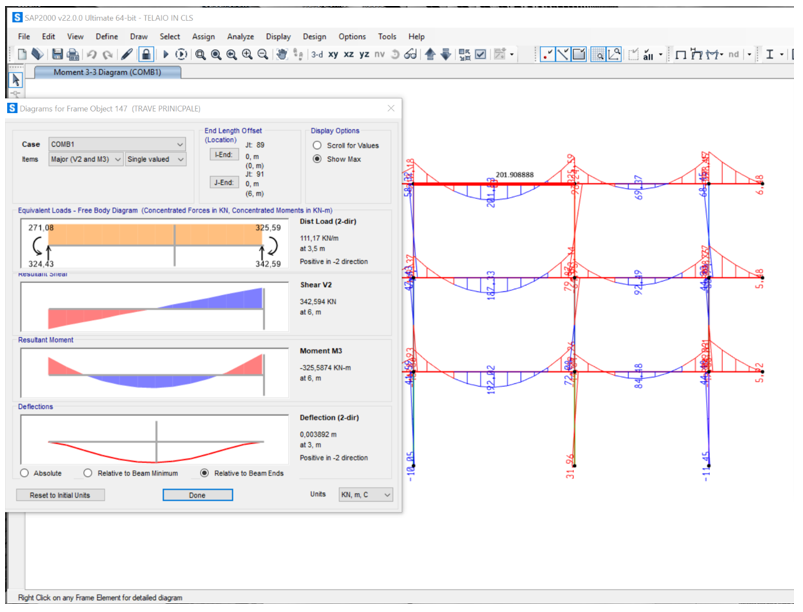
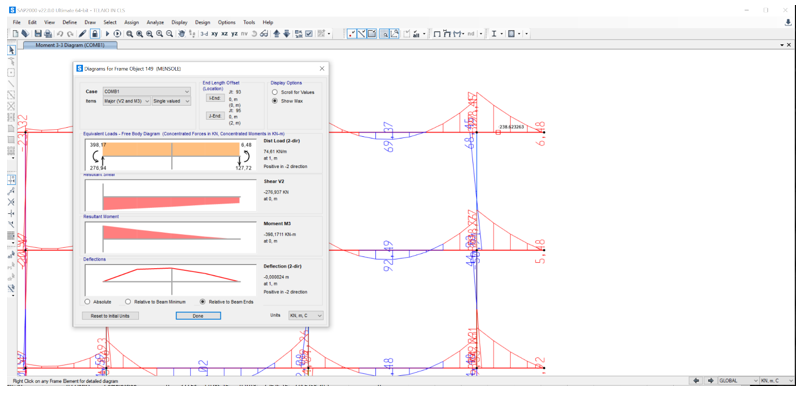
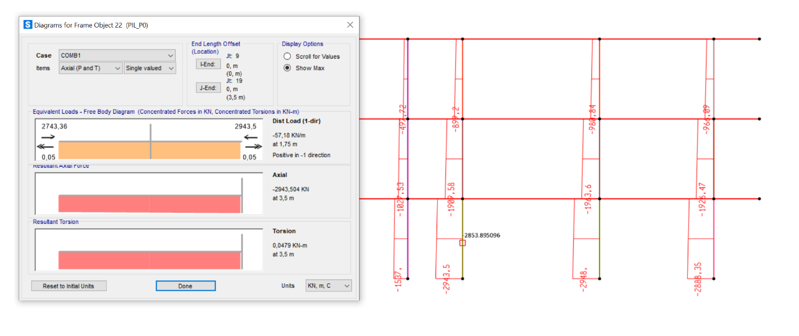
PILASTRI
PILASTRI P.T. CENTRALI IN CLS28/32 (40x40) FRAME 49
- N = 2952 kN
- M = 31,6
- e = M:N = 0,010m à 1cm
1cm < H/6 PICCOLA ECCENTRICITÀ
Fcd = 15,9 Mpa
I (Momento d’Inerzia) = (b*hᶟ)/12 = 213333,33 mᶟ
Wx (Modulo di resistenza a flessione) = (b*h2)/6 = 10666,66 mᶟ
σN = (N*10):A = 18,45 Mpa
σm = (M*1000):Wx = 2,96 Mpa
σMax = 21,41 Mpa > fcd NON VERIFICATO (dobbiamo scegliere pilastri rettangolari)
PILASTRI CENTRALI PIANO PRIMO (35x35) FRAME 117
- N = 1998,8 kN/m
- M = 47,83 kN/m
- e = M:N = 0,24m à 24cm à H/6 < 24cm < H/2 MODERATA ECCENTRICITÀ
Fcd = 15,9 Mpa
I = bhᶟ/(12) = 125052, 08 cm4
Wx = bh2/6 = 7145, 83 cm3
σN = 16,27 Mpa
σM = 4,48 Mpa
σMax = σN + σM = 20,75 > fcd NON VERIFICATA (dobbiamo scegliere un pilastro a sezione rettangolare)
PILASTRI CENTRALI PIANO 2 (30x30) FRAME 185
- N = 1012,4 kN
- M = 33,42 kN/m
- e = M:N = 0,33m à 33cm à H/6 < 33cm < H/2 MODERATA ECCENTRICITÀ
fcd = 15,9 Mpa
I = bhᶟ/(12) = 67500 Mpa
Wx = bh2/6 = 4500 Mpa
σN = 11,24 Mpa
σM = 7,42 Mpa
σMax = σN + σM = 18,66 > fcd NON VERIFICATA (dobbiamo scegliere un pilastro a sezione rettangolare)
Render:

Commenti recenti