ES.4-TRAVE VIERENDEEL

ESERCITAZIONE 4

COME FUNZIONA UNA VIERENDEEL

Ipotizzo una trave Vierendeel doppiamente appoggiata secondo lo schema presentato.

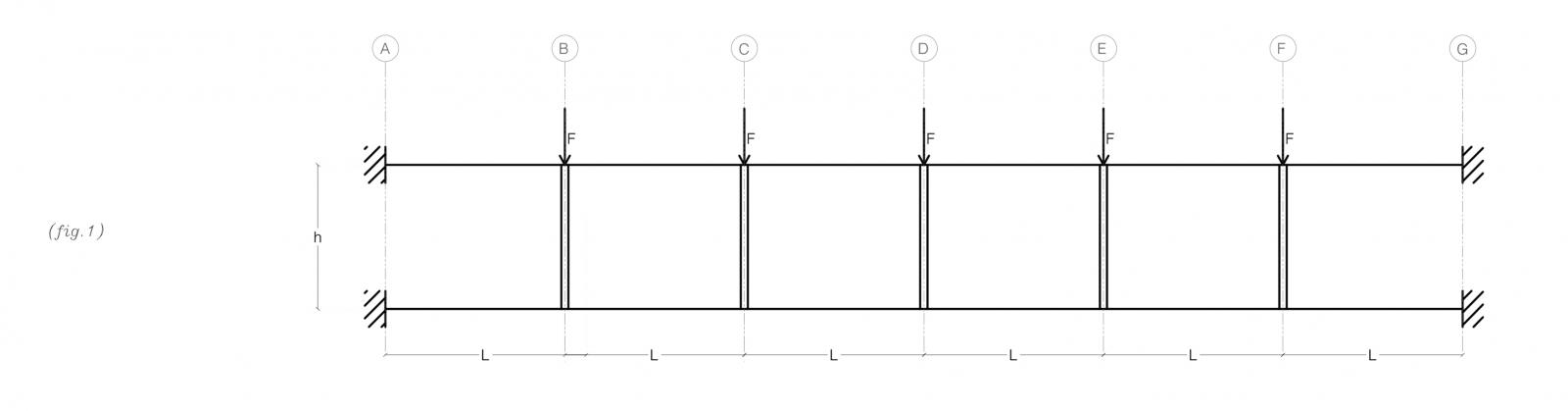
Dal punto di vista statico posso considerarla come la composizione di tanti telai SHEAR-TYPE rovesciati. Quindi come un elemento dove il componente TRAVE è caratterizzato da un elevata RIGIDEZZA FLESSIONALE e i componenti PILASTRI come INFINITAMENTE RIGIDI ASSIALMENTE. La rigidezza (K) è esprimibile come il rapporto tra una forza (F) e  lo spostamento (δ).

K=F/δ
F=Kδ

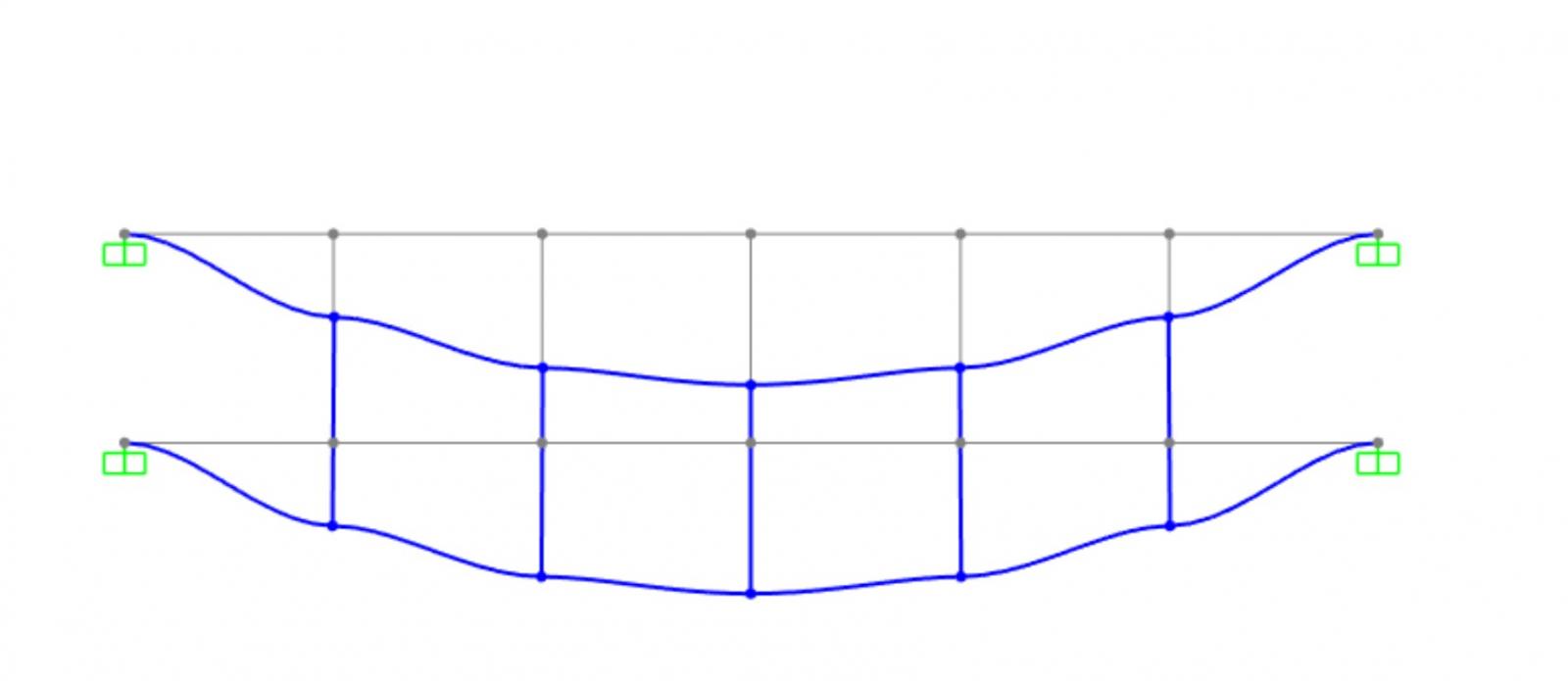
Secondo quanto appena detto la struttura sottoposta ad una forza F si deforma come una trave doppiamente incastrata sottoposta a cedimento vicolare elastico all’incastro.

Tramite le equazioni della linea elastica posso ricavarmi i valori di rotazione, spostamento, moment flettente e taglio.

EI dv⁴/ds + q=0

ν(s)=(12/l³)δ(s³/3)-(6/l²)δ(s²/2)

φ(s)=(12/l³)δs²/2-(6/l²)δs

χ(s)=12/l³δs-6/l²δ

M(s)=EIχ(s)=12EI/l³ δs- 6EI/l² δ

T(s)=-dM/ds=-12EI/l³ δ

Ritornando all’ipotesi presentata, i pilastri hanno tutti la stessa rigidezza, di conseguenza la forza F viene ripartita secondo uno schema prevedibile dato che la struttura presenta sia una simmetria geometrica che di carico.

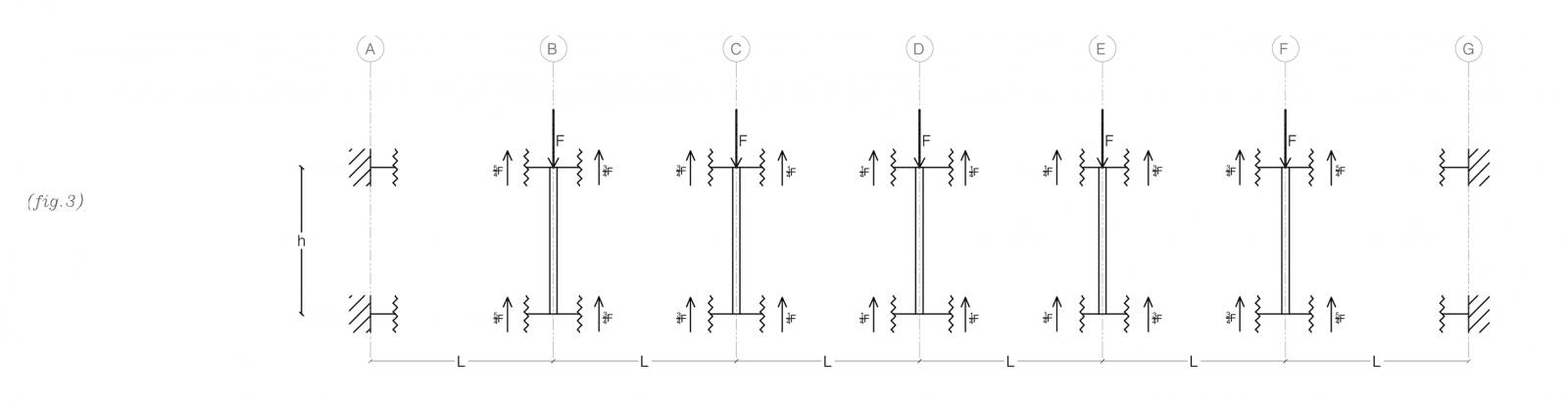
TAGLIO NELLE TRAVI*

T_CD=-F/4=-T_DE

T_BC=-F/4-F/2=-3/4F=-T_EF

T_AB=-F/4-2/2F=-5/4F=-T_FG

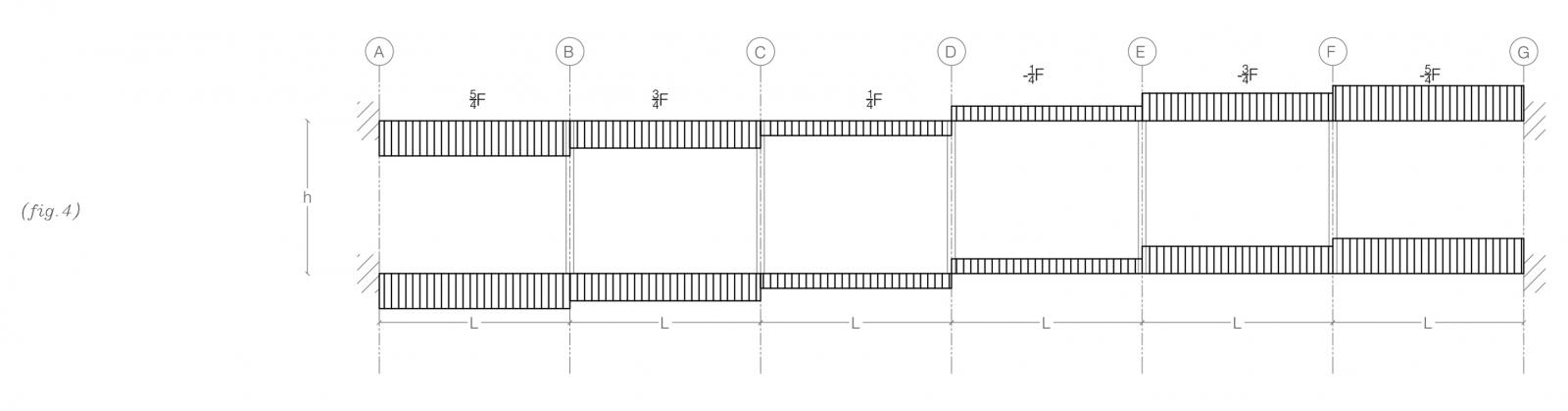
MOMENTO FLETTENTE NEI NODI

M=T*h/2

M_A=5/4F*h/2=5/8Fh=M_G

M_B=3/4F*h/2=3/8Fh=M_F

M_C=F/4*h/2=Fh/8=M_E

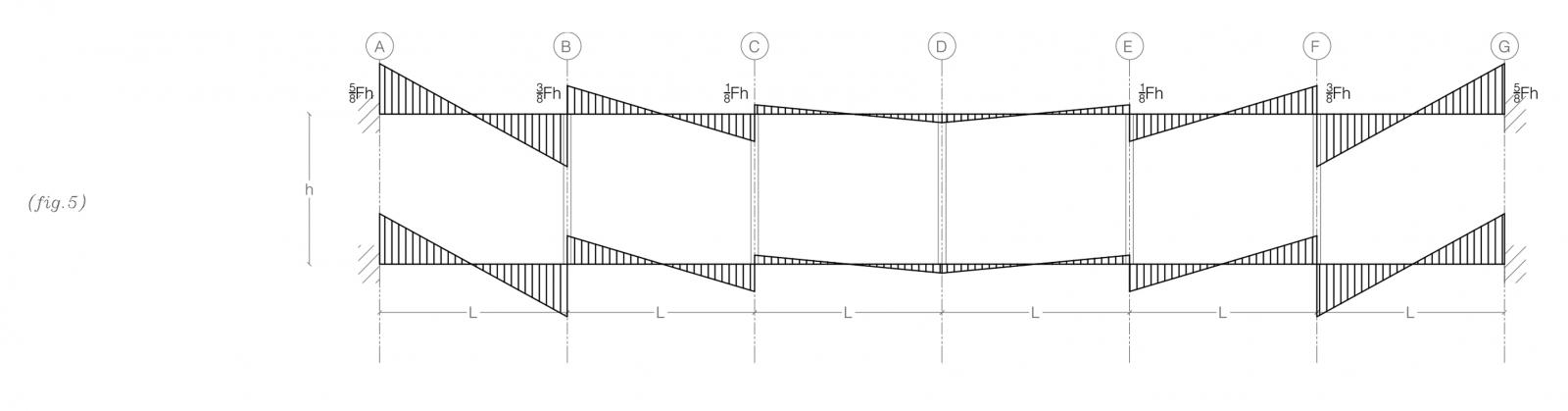
EQUILIBRIO AI NODI

Tramite l’equilibrioai nodi mi trovo TAGLIO e MOMENTO dei PILASTRI.

(astaB)
M=3/8Fh+Fh/8=Fh/2
T=(Fh+Fh)/l=2Fh/l

(astaC)
M=5/8Fh+3/8Fh=Fh
T=(2Fh/2)/l=Fh/l

(astaD)
M=Fh/8-Fh/8=0
T=0

SPOSTAMENTI

(tratto CD)

F/2=2T       F=4T          F=4 *12EI/h^{3 *} δ₃     δ₃=Fh³/48EI

(tratto CD)

F+2F/4=2T     F=4/3T     F=4/3*12EI/h^{3 *} δ₂     δ₂=Fh³/16EI

(tratto AB)

F+2*3/4F=2T     F=4/5T     F=4/5*12EI/h^{3 *} δ₁    δ₁=5/48 * Fh³/EI

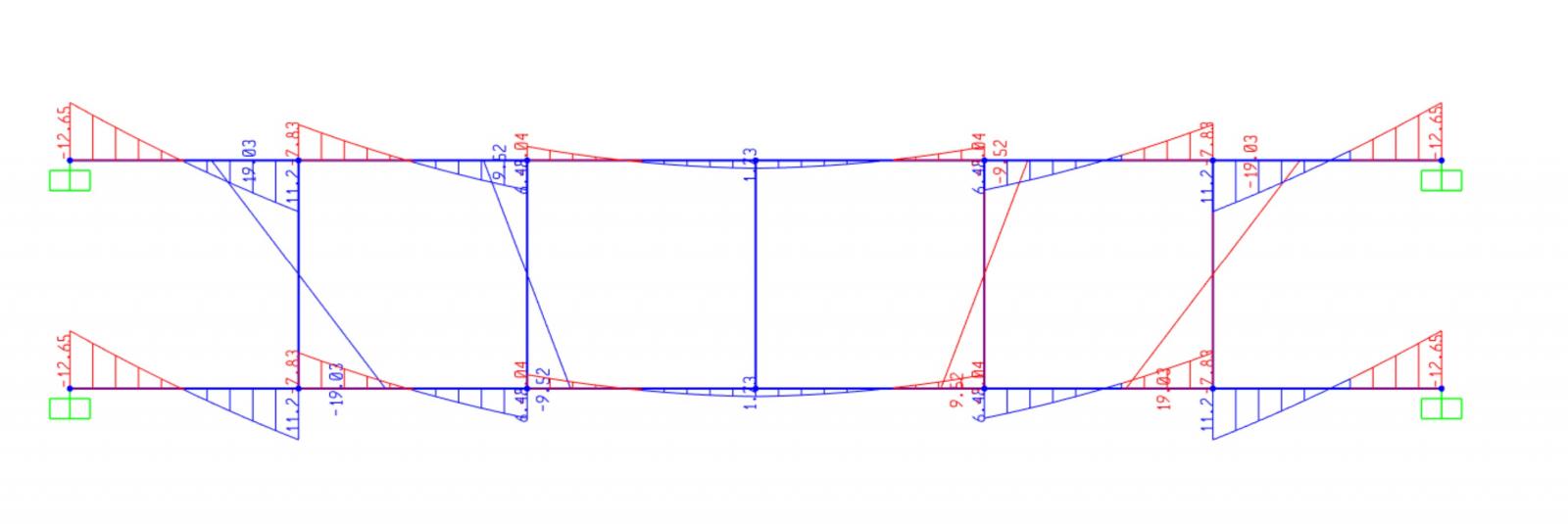
VERIFICA IN SAP2000

Tutto ciò è possibile verificarloin Sap attribuendo agli elementi "pilastri" della nostra struttura una sezione estremamente grande (agendo sull momento d'inerzia) o un  materiale con un modulo elastico estremamente grande per esprimere il concetto dell' INFINITAMENTE RIGIDO. Avviando l'analisi osserviamo che deformate e digrammi corrispondono a quanto precedentemente visto.