ESERCITAZIONE 5- PIASTRA O GRATICCIO?
ESERCITAZIONE 5
PIASTRA O GRATICCIO?
DESCRIZIONE DEL CASO
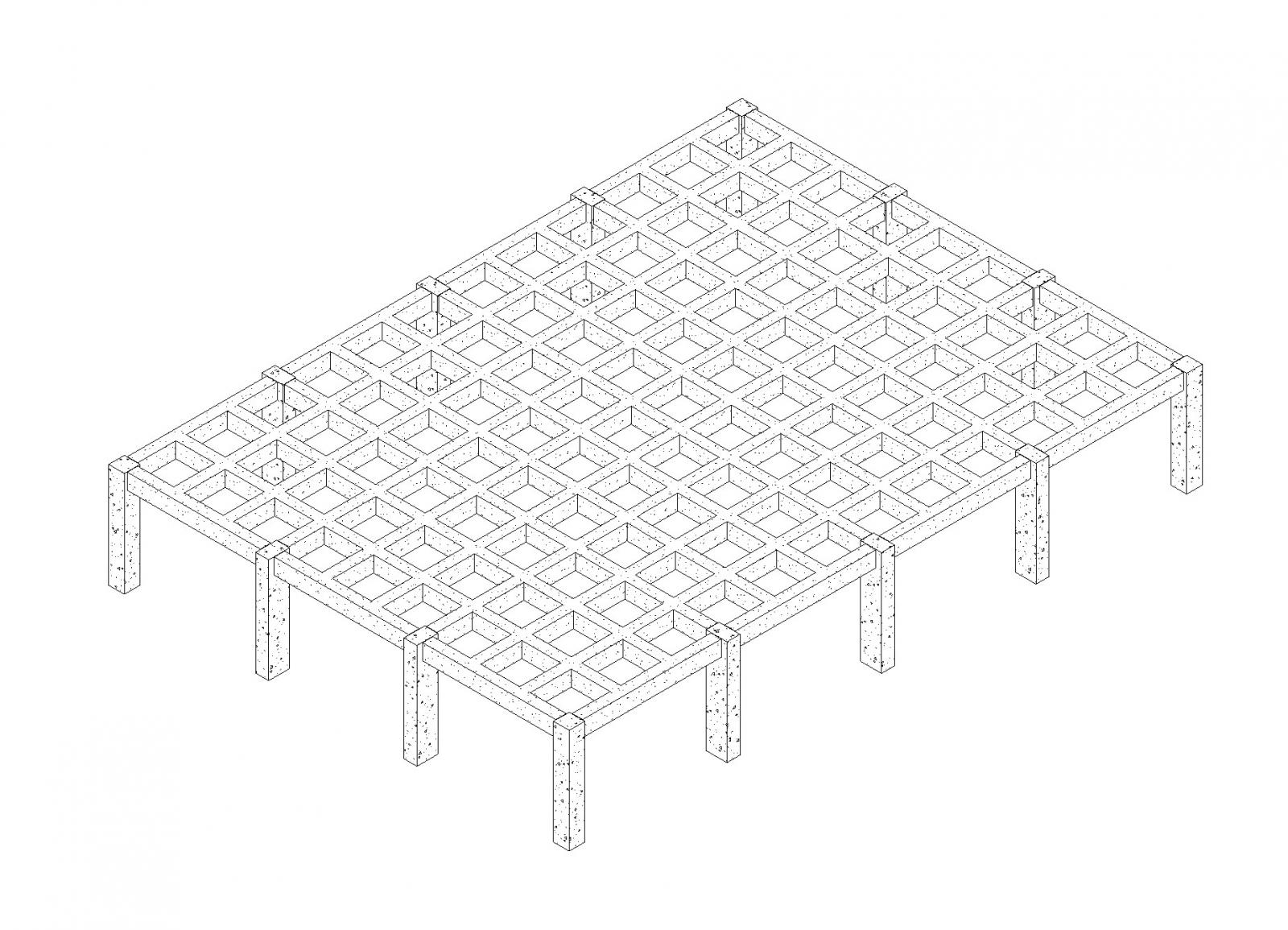
Nella seguente esercitazione porto come caso studio una parte del progetto che sarà presentato all’esame. Nello specifico si tratta di un area interrata adibita a parcheggio (23.63m *17m), per questo ho la necessita di trovare una risposta strutturale che mi permetta di coprire luci che iniziano ad essere importanti lasciandola l’area sottostante libera dai pilastri.
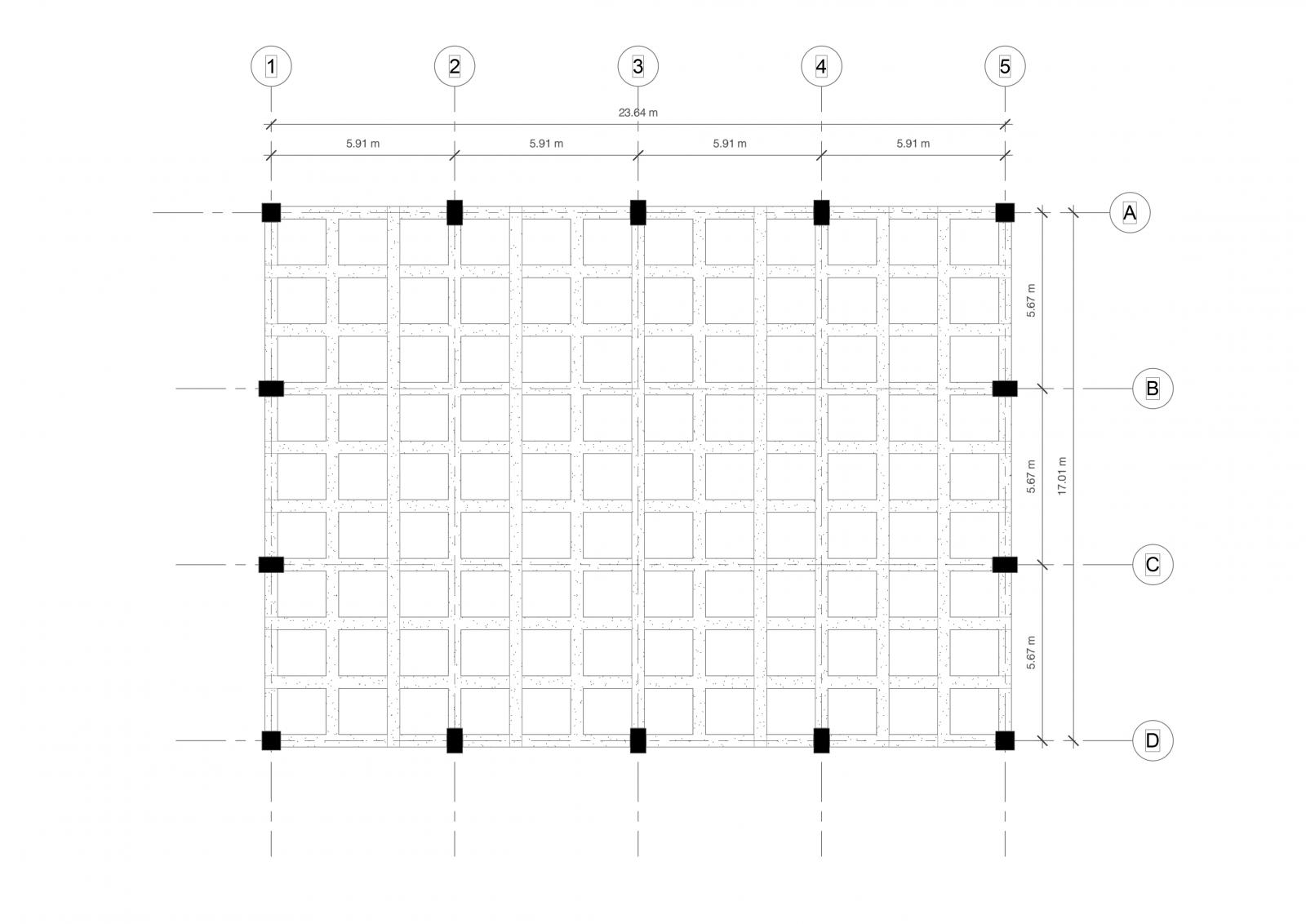
L’interogativo, che è lo stesso a qui siamo posti per questa esercitazione è:
“Per risolvere strutturalmente la copertura uso una piastra o un graticcio di travi?”
RIFLESSIONE
Benché entrambe strutturalmente potrebbero essere la soluzione al problema, i parametri che variano sono molteplici e non rivestono solo l’ambito del comportamento meccanico. A parità di carico, un piastra pesa di più di un graticcio di travi (in funzione dell’interasse di quest’ultimo, ovvio che più la maglia di quest’ultimo sarà stretta, più questo sarà paragonabile ad una piastra). Da un punto di vista cantieristico la realizzazione di una piastra è più semplice di quella di un graticcio( dato il montaggio delle casseforme), ma analogamente il dispendio di materiale è superiore incidendo sull’ economia del progetto).
ANALISIDEI CARICHI
I carichi agenti sulla copertura del parcheggio sono quelli dovuti al metro di terreno di riporto sulla sommità e quello accidentale delle persone che ci camminano sopra( per quest’ultimo si è considerato come una zona soggetta a grande affollamento come caso estremo).
| L | l | s | γ | ||
| m | m | m | N/m3 | ||
| Terreno | 17.01 | 23.63 | 1 | 19.6133 | 7883.493 |
| Accidentale | 5 | 2009.732 | |||
| 9893.225 |
RIPARTIZIONE DEI CARICI NELLA PIASTRA
Per quanto riguarda la modellazione in SAP2000 si è preso arbitrariamente una sezione di altezza 0.6m per la piastra. Quest’ultima è stata modellata suddividendola in sottomultipli delle dimensione del parcheggio.
I carichi possono essere considerati puntuali nei nodi in cui ho diviso la piastra ( n.b. potrei considerarli anche distribuiti calcolando le singole aree di influenza). La regola rimane che i nodi al centro si prenderanno il l’intero quantitativo del carico al mq derivante dall’analisi dei carichi (diviso il numero dei nodi), quelli al bordo ½ e quelli agli angoli ¼.
| n | F | ||
| NODI CENTRALI | 1131 | 8.24 | |
| NODI BORDO | 68 | 4.12 | |
| NODI ANGOLO | 1 | 2.06 | |
| 1200 |
Caricata la struttura posso leggere i valori del momento flettente e dell’abbassamento. Si nota che i valori più rilevanti, riguardo il momento si hanno sul appoggio con i pilastri di bordo. La disposizione di questi, nello specifico la loro inerzia influenza la flessione della piastra.( n.b. i pilastri dovrebbero sempre garantire il momento d’inerzia superiore offerto dalla sua sezione, in asse con la flessione della piastra).
E’ QUI CHE AVVIENE LO SWITCH!
Riprendendo la domanda principale, “piastra o graticcio?”, prendo il valore massimo di Momento Flettente e predimensiono un’ipotetica trave che abbia come base lo spessore della piastra. Se l’altezza utile è molto inferiore o superiore allo spessore della piastra si innesca un processo di iterazione dove gradualmente diminuendo o aumentando lo spessore della mia piastra verifico questa.(n.b. questo processo di iterazione può comportare la definizione di piastre con spessori tali che non sono plausibili, dato che si arriverà a casi dove il peso stesso della piastra svilupperà reazioni esagerate che richiedono una grande dimensione degli appoggi). Se da questo predimensionamento non si hanno drastiche differenze geometriche con lo spessore scelto, si può anche ipotizzare di convertire la piastra in un graticcio di travi.
| Mmax (KN*m) | fyk (N/mm2) | fyd (N/mm2) | fck (N/mm2) | fcd (N/mm2) | β | r | b (cm) | hu (cm) | δ (cm) | Hmin (cm) |
| 1954.50 | 450.00 | 391.30 | 50.00 | 28.33 | 0.52 | 2.16 | 60.00 | 73.10 | 5.00 | 78.10 |
RIPARTIZIONE DEI CARICHI NEL GRATICCIO
Nota la campata tra gli appoggi al bordo, posso suddividerla in sottocampate che saranno gli assi delle travi del mio graticcio.
Mi calcolo il Momento d’Inerzia di una fascia di piastra, di dimensioni analoghe all’area di influenza delle travi del graticcio. Lo scopo è quello di dimensionare delle travi che garantiscono la stessa inerzia flessionale della piastra. Per fare questo ipotizzo una base per la trave del mio graticcio e tramite la formula inversa mi ricavo l’altezza utile necessaria.
I=1/12 bh^3
h=(12I/b)^1/3
Anche qui si innesca un processo di iterazione per il quale variano le dimensioni del pilastro o diminuendo le dimensioni della maglia riesco a garantire lo stessa inerzia.
| s | interasse | I | b | h |
| m | m | m^4 | m | m |
| 0.6 | 1.89 | 0.034 | 0.3 | 0.4536 |
| 0.6 | 1.97 | 0.035 | 0.3 | 0.4726 |
Nel caso riportato ho suddiviso le campate tra i singoli appoggi in 3 parti uguali. Questo mi ha permesso di ottenere delle travi di dimensione 300x500mm per il mio graticcio.
La ripartizione dei carichi ora è analoga a quanto già fatto per la piastra.
Avviata l’analisi posso verificare l’abbassamento e la pressoflessione dei pilastri.
| Pilastri | L | b | h | A | Wx | fck | fcd | N | M | e | h/6 | h/2 | sigma_N | sigma_M | sigma_max | |||||
| m | cm | cm | cm^2 | cm^3 | Mpa | Mpa | kN | kNm | cm | cm | cm | Mpa | Mpa | Mpa | ||||||
| Piccola Eccentricità | ||||||||||||||||||||
| 4 | 4 | 50 | 80 | 4000 | 53333.333 | 50.00 | 28.33 | -1192.2 | 37.4942 | 3.14 | 13.333333 | 40.0 | Piccola | 2.98 | 0.70 | 3.68 | Verificata | |||
| 5 | 4 | 50 | 80 | 4000 | 53333.333 | 50.00 | 28.33 | -1545.91 | 1.1E-12 | 0.00 | 13.333333 | 40.0 | Piccola | 3.86 | 0.00 | 3.86 | Verificata | |||
| 6 | 4 | 50 | 80 | 4000 | 53333.333 | 50.00 | 28.33 | -1192.2 | -37.4942 | 3.14 | 13.333333 | 40.0 | Piccola | 2.98 | -0.70 | 2.28 | Verificata | |||
| 8 | 4 | 50 | 80 | 4000 | 53333.333 | 50.00 | 28.33 | -1079.41 | 28.7142 | 2.66 | 13.333333 | 40.0 | Piccola | 2.70 | 0.54 | 3.24 | Verificata | |||
| 9 | 4 | 50 | 80 | 4000 | 53333.333 | 50.00 | 28.33 | -1079.41 | -28.7142 | 2.66 | 13.333333 | 40.0 | Piccola | 2.70 | -0.54 | 2.16 | Verificata | |||
| 11 | 4 | 50 | 80 | 4000 | 53333.333 | 50.00 | 28.33 | -1192.2 | 37.4942 | 3.14 | 13.333333 | 40.0 | Piccola | 2.98 | 0.70 | 3.68 | Verificata | |||
| 12 | 4 | 50 | 80 | 4000 | 53333.333 | 50.00 | 28.33 | -1545.91 | 2.535E-12 | 0.00 | 13.333333 | 40.0 | Piccola | 3.86 | 0.00 | 3.86 | Verificata | |||
| 13 | 4 | 50 | 80 | 4000 | 53333.333 | 50.00 | 28.33 | -1192.2 | -37.4942 | 3.14 | 13.333333 | 40.0 | Piccola | 2.98 | -0.70 | 2.28 | Verificata | |||
| 15 | 4 | 50 | 80 | 4000 | 53333.333 | 50.00 | 28.33 | -1079.41 | -28.7142 | 2.66 | 13.333333 | 40.0 | Piccola | 2.70 | -0.54 | 2.16 | Verificata | |||
| 16 | 4 | 50 | 80 | 4000 | 53333.333 | 50.00 | 28.33 | -1079.41 | 28.7142 | 2.66 | 13.333333 | 40.0 | Piccola | 2.70 | 0.54 | 3.24 | Verificata | |||
| β | r | hu | δ | Hmin | H | |||||||||||||||
| cm | cm | cm | cm | |||||||||||||||||
| Piccola Eccentricità | ||||||||||||||||||||
| 1 | 4 | 70 | 70 | 4900 | 57166.667 | 50.00 | 28.33 | -114.725 | 197.9718 | 172.56 | 11.666667 | 35.0 | Grande | 0.73 | 1.91 | 17.14 | 5.00 | 22.14 | 40.00 | Verificata |
| 7 | 4 | 70 | 70 | 4900 | 57166.667 | 50.00 | 28.33 | -114.725 | -197.9718 | 172.56 | 11.666667 | 35.0 | Grande | 0.73 | 1.91 | 17.14 | 9.00 | 26.14 | 44.00 | Verificata |
| 10 | 4 | 70 | 70 | 4900 | 57166.667 | 50.00 | 28.33 | -114.725 | 197.9718 | 172.56 | 11.666667 | 35.0 | Grande | 0.73 | 1.91 | 17.14 | 12.00 | 29.14 | 47.00 | Verificata |
| 14 | 4 | 70 | 70 | 4900 | 57166.667 | 50.00 | 28.33 | -114.725 | -197.9718 | 172.56 | 11.666667 | 35.0 | Grande | 0.73 | 1.91 | 17.14 | 16.00 | 33.14 | 51.00 | Verificata |
Per quanto riguardal'abbassamento ho invece:
| Joint | U1 | U2 | U3 |
| Text | mm | mm | mm |
| 160 | 7.452E-15 | 0.0606 | -45.68567 |
| 161 | 7.931E-15 | -0.0606 | -45.68567 |