Quinta Esercitazione: Il Graticcio. Studentesse: Arianna Sofia Pace, Giulia Retacchi

La struttura di dimensioni 40 m x 40 m x 4 m sostiene il peso di 4 piani ed è composta da un graticcio sorretto da 5 pilastri per lato che garantisce di avere al di sotto di esso uno spazio completamente libero e aperto.

Una volta stabilito il tipo di struttura e le sue caratteristiche, abbiamo portato il modello su SAP cominciando definendo le sezioni dei pilastri che abbiamo posizionato ogni 10 m con un calcestruzzo ad alte prestazioni C50/60

- Pilastri angolari: 1 m x 1 m

- Pilastri laterali: 1,2 m x 0,6 m

E' necessario verificare che i pilastri siano orientati in modo corretto dal momento che SAP li orienta di default tutti alla stessa maniera, invece noi abbiamo bisogno che l'inerzia maggiore sia nella stessa direzione delle travi che compongono il graticcio.

Assegnamo il vincolo esterno Incastro alla base di ogni pilastro e disegnamo il graticcio all'inizio sotto forma di una piastra (successivamente disegneremo il vero e proprio graticcio) con lo strumento Draw polyarea e gli assegamo una sezione di 1 m x 1 m.

E' necessario che, nella definizione della piastra, noi andiamo a modificare il materiale, più precisamente il coefficiente di Poisson che poniamo uguale a zero. Facendo ciò simuliamo il comportamento di un sistema discretizzato dove non ci sono deformazioni ntroducendo un materiale fittizio per simulare un continuo bidimensionale . Il coefficiente di Poisson infatti tiene conto della diminuzione di dimensione in corrispondenza dell'allungamento in seguto a uno sforzo normale positivo.

Per assegnare i carichi prima è necessario discretizzare la superficie della piastra/shell in quanto più discretizziamo la superficie più i risultati saranno accurati. Dividiamo dunque la superficie in porzioni di 0,50 m x 0,50 m.

Il carico consiste in 10 kN/mq per piano, moltiplicandolo per l'area e il numero dei piani otterremo il carico puntale (64.000 kN) che verrà assbito dalla piastra dai nodi centrali, ancolari, perimetrali. I nodi centrali sono 6241, quelli perimetrali 316, quelli angolari 4. Considerando che sui centrali andrà la totalità del carico, sui perimetrali la metà e sugli angolari un quarto:

64.000 / (6241+158+1) = 9,73 kN che è circa uguale a 10 kN

- Sui nodi centrali verranno trasferiti 10 kN di carico

- Sui nodi laterali 5 kN

- Sui nodi angolari 2,5 kN

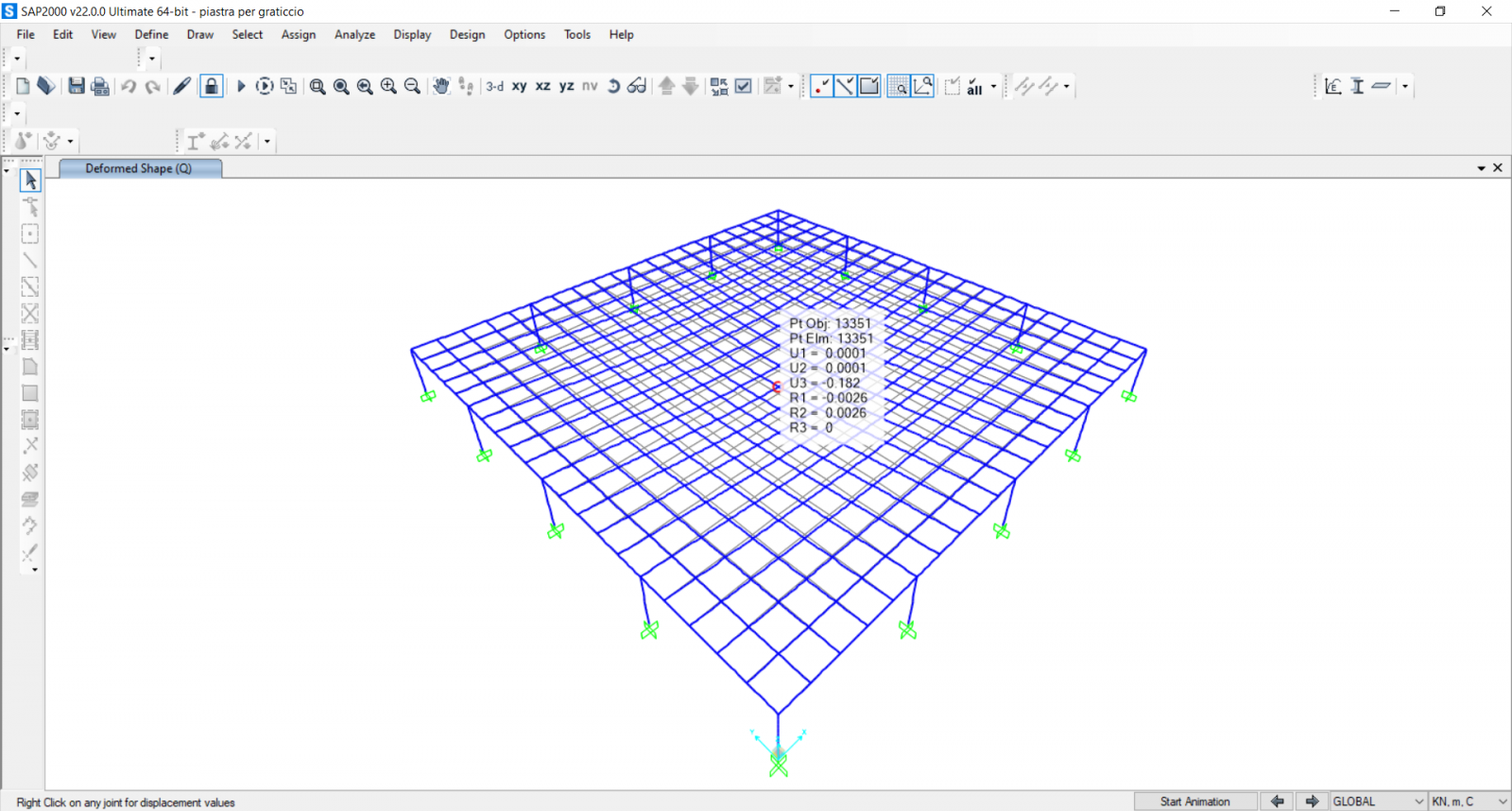
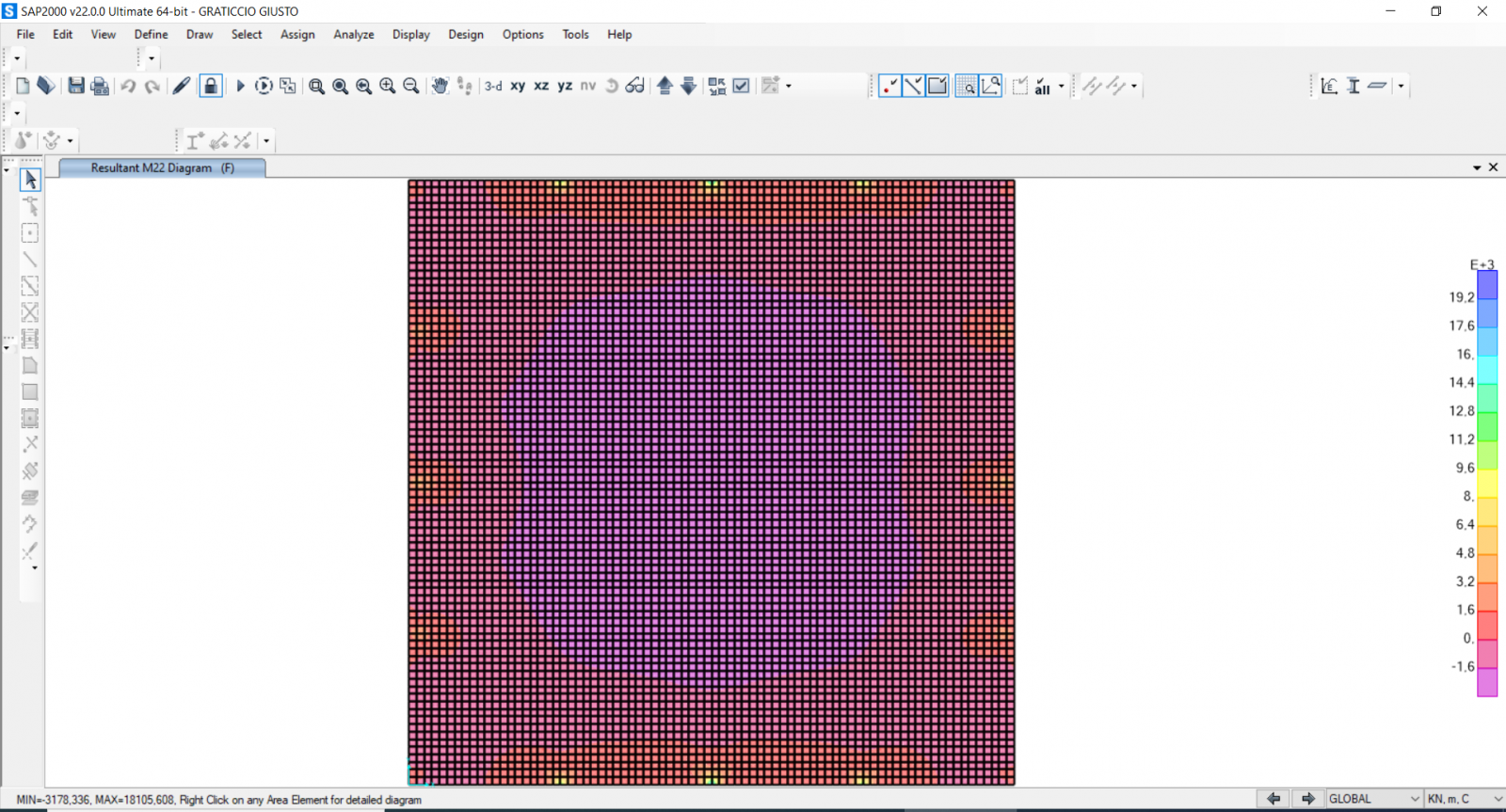
Assegnamo tali carichi a ciascun nodo su Sap dopo aver creato il caso di carico F che terrà conto del peso proprio degli elementi e mandiamo l'analisi. Osserviamo i diagrammi di normale, taglio e momento  dei pilastri, la deformazione della piastra,dai cui deduciamo che l'abbassamento è accettabile in quando di circa 2 cm e il momento massimo della piastra pari a 25694 kNm.

Grafico della Normale:

Grafico del Taglio:

Grafico del Momento:

Grafico della deformazione della piastra:

Grafico del momento della piastra:

Inserendo il valore del momento massimo della piastra all'interno del foglio Excell posso dedurre l'altezza effettiva della piastra ovvero 1,77 (vedi riga gialla):

Possiamo passare direttamente al progetto del graticcio considerando l'altezza della piastra accettabile. Successivamente poniamo l'interasse delle travi del graticcio uguale a 2 m.

Se ci calcoliamo l'inerzia di 2 m x 1 m di piastra con la formula Ix = b x h^3 / 12 troviamo l'inerzia che dovrà avere ogni trave del graticcio. 

Successivamente se usiamo la formula inversa e scegliamo la dimensione della base della trave (0,50 m) otterremo l'altezza della trave del graticcio:

Ix = b x h^3 / 12 = (2 x 1^3 ) /12 = 0,16

h = [ (Ix x 12)/b ] ^1/3 = [ (0,16 x 12 ) / 0,50 ] ^1/3 = 1,56 => 1,70 m

Possiamo dunque sostituire la piastra progettando il graticcio con tali sezioni 1,70 m x 0,50 m

Creiamo il nuovo caso di carico Q e calcoliamo i carichi allo stesso modo della piastra:

64.000 kN / 361 nodi centrali + 38 nodi perimetrali + 1 nodo angolare = 160 kN

- Sui nodi centrali verranno trasferiti 160 kN di carico

- Sui nodi laterali 80 kN

- Sui nodi angolari 40 kN

E mandiamo nuovamente l'analisi:

Diagramma del momento massimo sul pilastro:

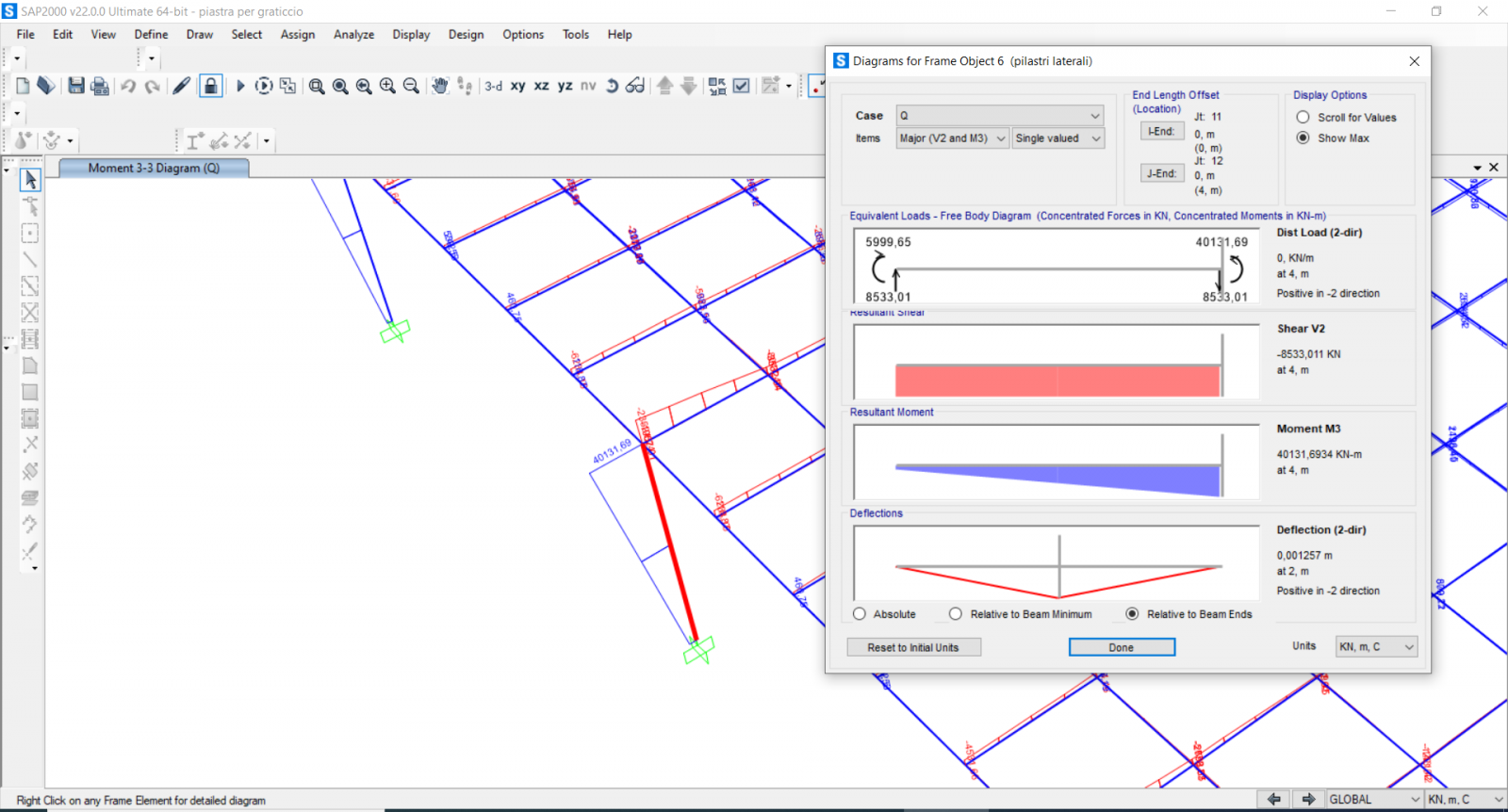
Diagramma del momento massimo sulla trave del graticcio:

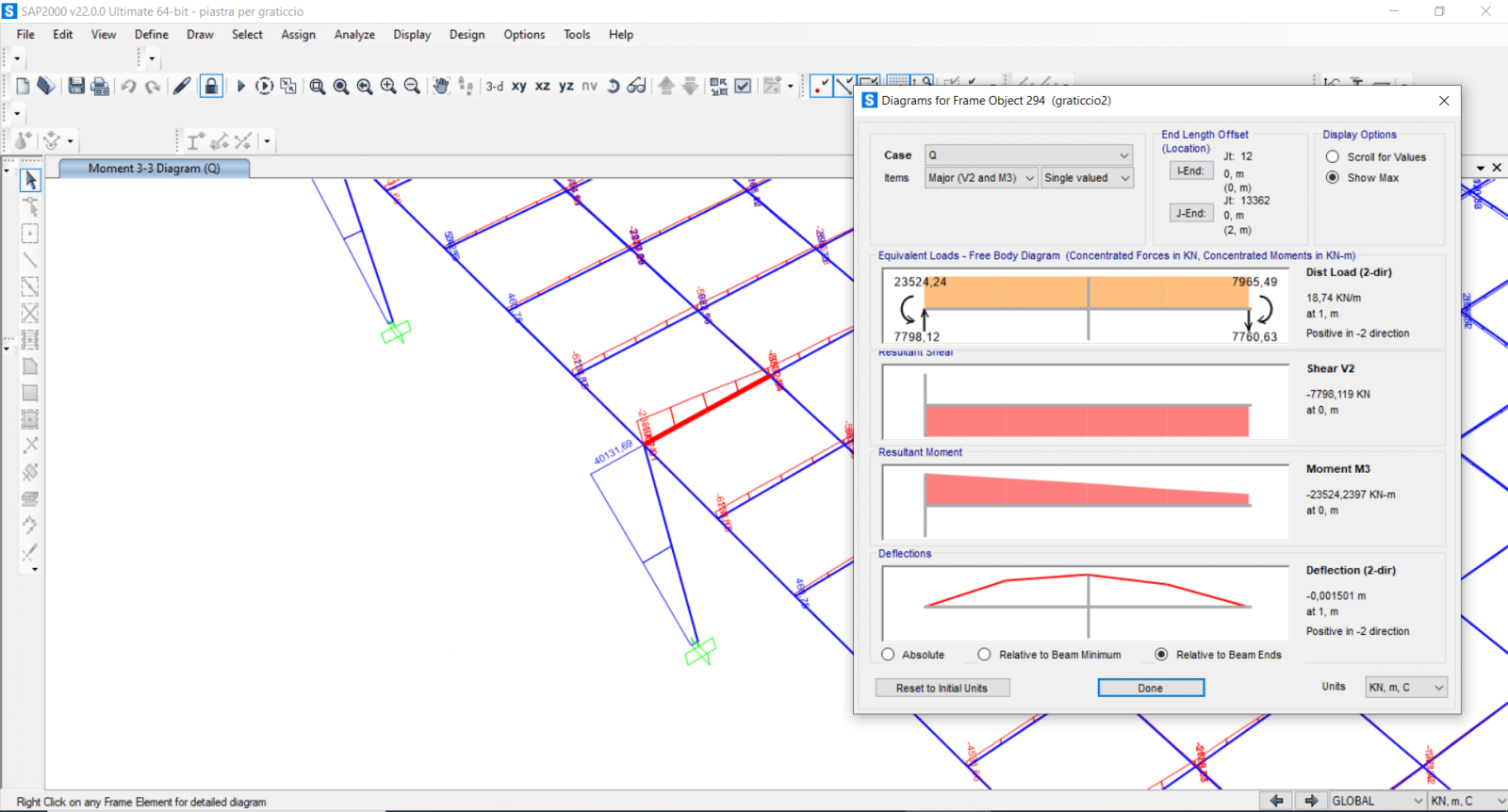
Notiamo che sui pilastri il momento massimo è molto alto poichè questo tipo di strutture tende a gravare molto sui sostegni su cui si poggia. Il momento massimo sui pilastri è pari a 40131,69 KNm e sulle travi del graticcio è pari a 23524,23 KNm. Per ridurre tale momento possiamo provare ad aumentare la sezione della trave di bordo in modo tale da modificarne la rigidezza per sopperire lei a tale momento. Aumentiamo dunque la sezione sia del pilastro che della trave di bordo utilizzando il foglio excell (vedi riga verde e rossa):

Se, come nel nostro caso, in momento non si riduce, ne sul pilastro e ne sulla trave di bordo, è necessario cambiare il tipo di sezione della trave di bordo. Per questo motivo assegno una seziione rettangolare cava, in quanto i profili cavi hanno una elevata rigidezza torsionale. Infatti se irrigidiamo la trave questa farà effetto 'incastro' in quanto non ruoterà a torsione e il momento si ridurrà notevolmente.

Diagramma del momento massimo pilastro:

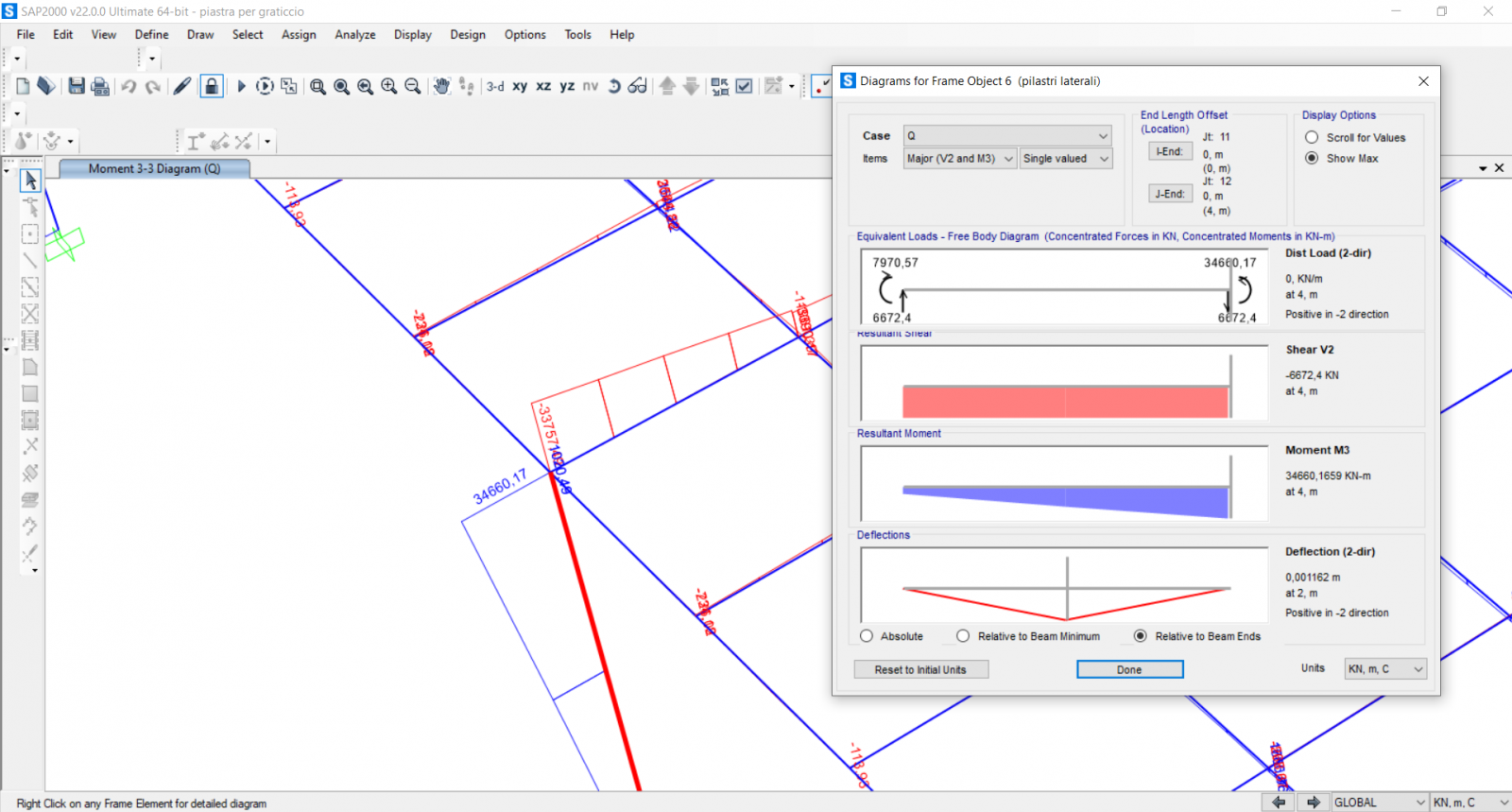
Diagramma del momento massimo sulla trave del graticcio:

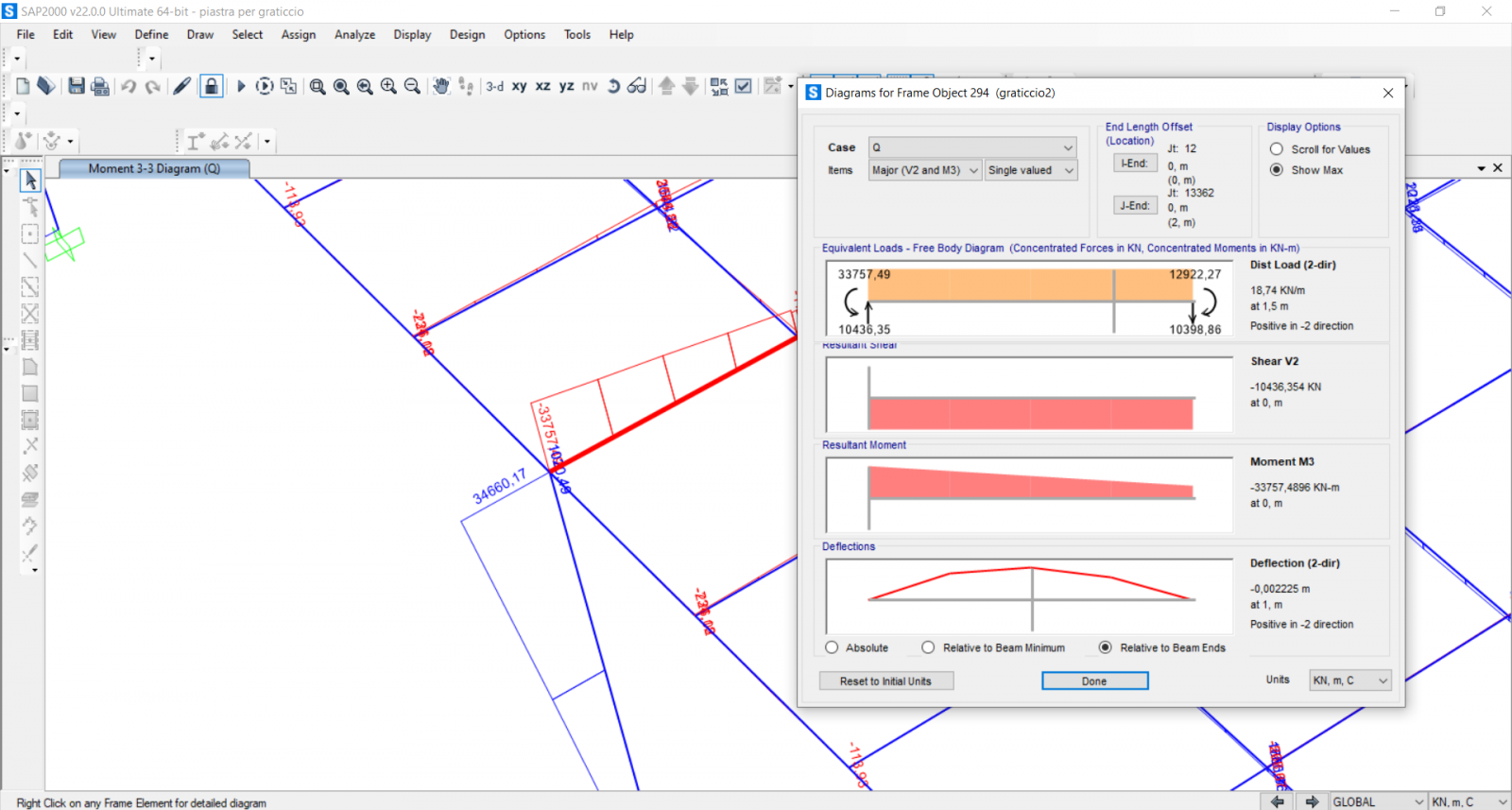
Diagramma deformazione verificata: