Esercitazione: Trave Vierendeel
Studentesse: Giulia Retacchi, Arianna Sofia Pace
Progetto di una trave Vierendeel
- Progetto preliminare dell’edificio
- Analisi dei carichi
- Definizione delle aree di influenza delle travi e dei pilastri
- Definizione del modello su SAP2000
- Verifica delle travi Vierendeel
- Analisi sollecitazioni
- Conclusioni teoriche sulla trave Vierendeel
1.Progetto preliminare dell’edificio:
Per la quarta esercitazione è stato scelto un telaio in cls armato, con un ampio sbalzo al secondo piano sostenuto grazie a una struttura composta da travi Vierendeel, collegate ad un setto di 30 cm di spessore.
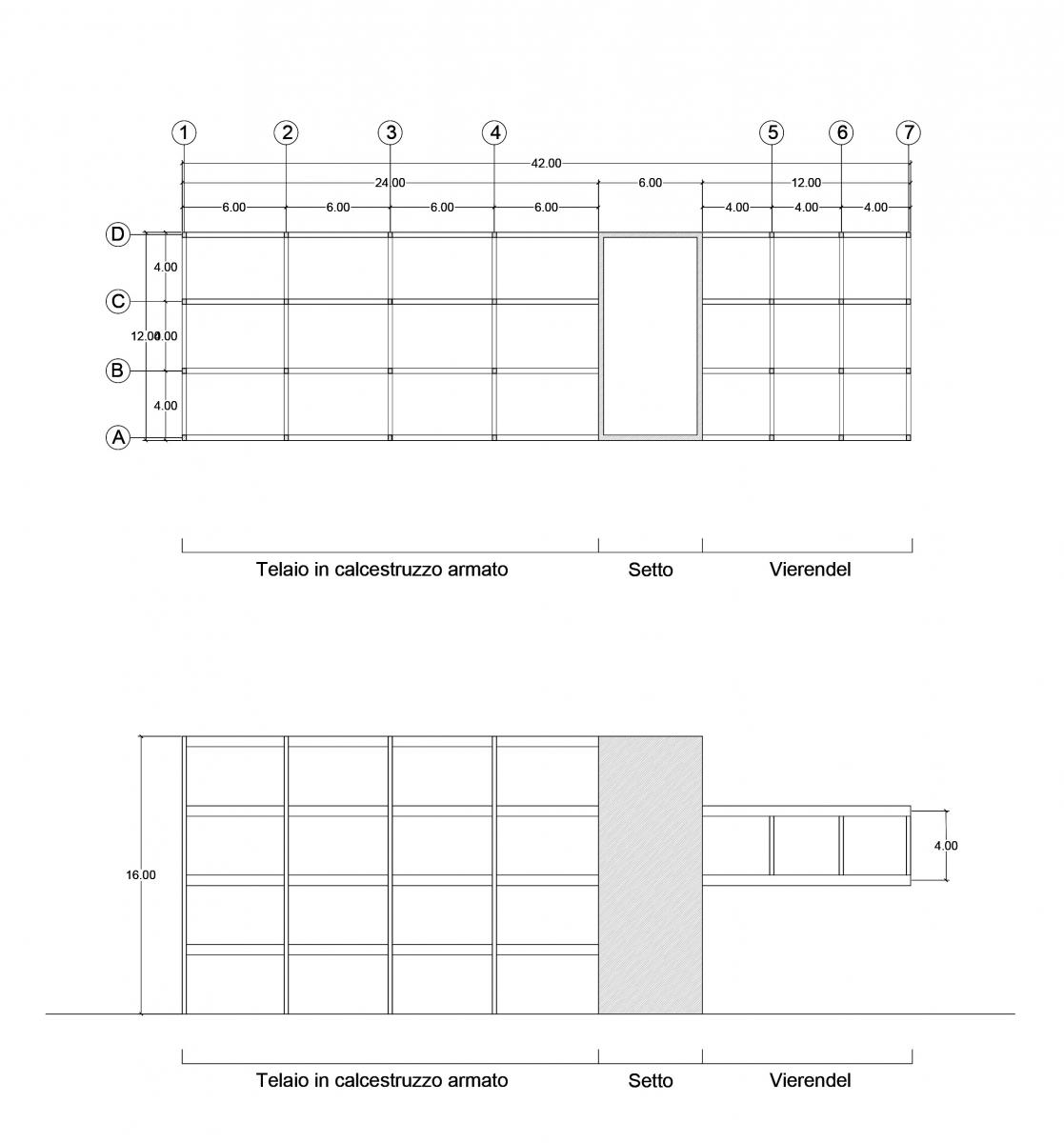
L’edificio, di dimensioni 42 m x 12 m, con destinazione “uffici aperti al pubblico”, è alto 16 m e comprende 4 piani, mentre lo sbalzo, di dimensioni 4 m x 4 m, si estende per un solo piano. La griglia è piuttosto regolare, le travi secondarie hanno tutte una luce di 4 m.
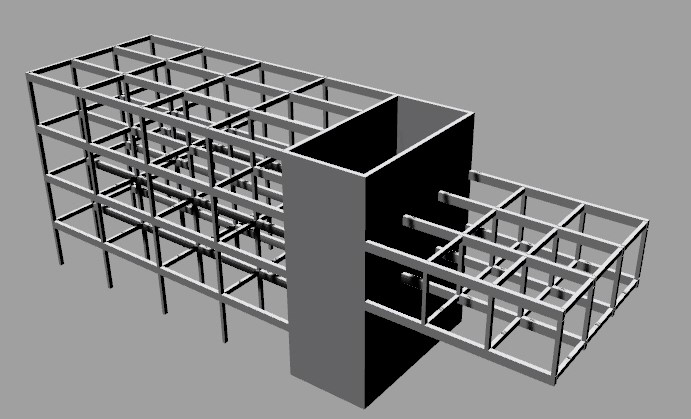
2.Analisi dei carichi ( s x γ):
Il solaio impiegato per la struttura è un classico solaio in cls composto da:
- Pavimento: 20 mm di Gres Porcelanato (γ 20 Kn/m3)
- Allettamento: 80 mm di allettamento (γ 20 kN/m3)
- Isolante: 30 mm di isolante (γ 1 Kn/m3)
- Massetto: 40 mm di massetto (γ 20 kN/m3)
- Getto in cls: 40 mm di getto in cls (γ 25 kN/m3)
- Pignatte: 200 mm di pignatte (γ 6 kn/m3)
- Intonaco: 20 mm di intonaco (γ20 kn/m3)
Le pignatte, larghe 380 mm sono intramezzate da travetti larghi 120 mm dello stesso spessore pignatte e travetti si ripetono uguali ogni 500 mm ovvero l’interasse.
qs (carico strutturale) = qs (soletta) + qs(pignatte) + qs (travetti) = (25 kN/m3 x 0,04 m) + (6 kN/m3 x 0,38 m x 0,20 m / 0,5 m) + (25 kN/m3 x 0,12 m x 0,20 m / 0,5 m) = 1 kN/m2 + 0,912 kN/m2 + 1,2 kN/m2 = 3,12 kN/m2
qp (sovraccarico permanente) = qp (gres)+ qp (massetto) + qp (isolante) + qp (intonaco) + qp (tramezzi) + qp (impianti) = (20 kN/m3 x 0,02 m) + (20 kN/m3 x 0,04 m + 0,08 m) + (1 kN/m3 x 0,03 m) + (20 Kn/m3 x 0,02 m) + 1kN/m2 + 0,5 kN/m2 = 0,4 Kn/m2 + 2,4 kN/m2 + 0,03 kN/m2 + 0,4 kN/m2 + 1 kN/m2 + 0,5 kN/m2 = 4,73 kN/m2
qa (sovraccarico accidentale) = 3 kN/m2
3.Definizione delle aree di influenza delle travi e dei pilastri:
Dal momento che ci siamo già occupati dell’analisi di un telaio in cls nelle precedenti esercitazioni proseguiamo occupandoci della struttura composta dalle quattro travi Vierendeel che sostengono la porzione di solaio a sbalzo di area 12m x 12m definendo l’area di influenza delle travi e dei pilastri che compongono questo sistema. È stata scelta questa struttura per l'enorme rigidezza dei montanti verticali per la quale la trave Vierendeel può essere assimilata ad un telaio SHEAR TYPE disposto orizzontalmente.
Area di influenza delle travi
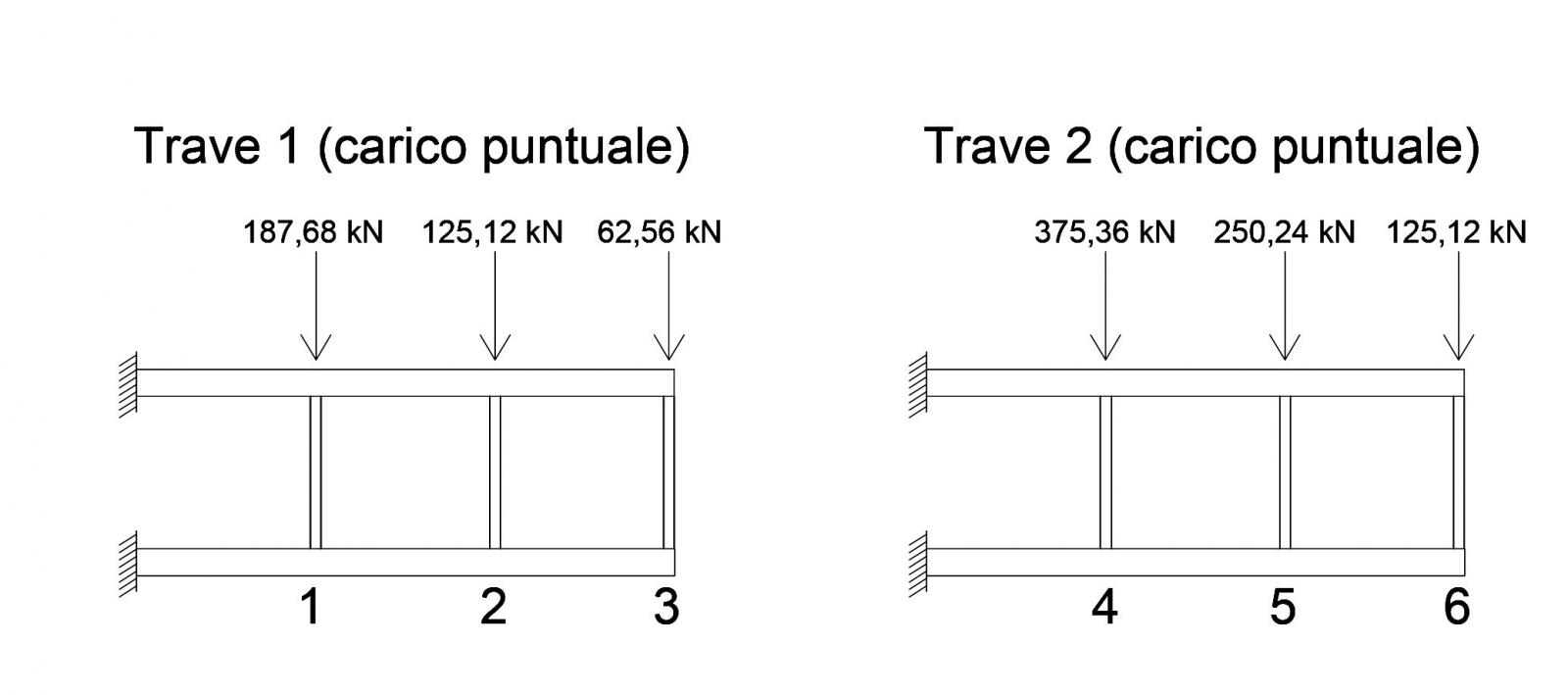
Si possono dunque distinguere due casi: quello della trave 1 e quello della trave 2 e di conseguenza due diverse aree di influenza.
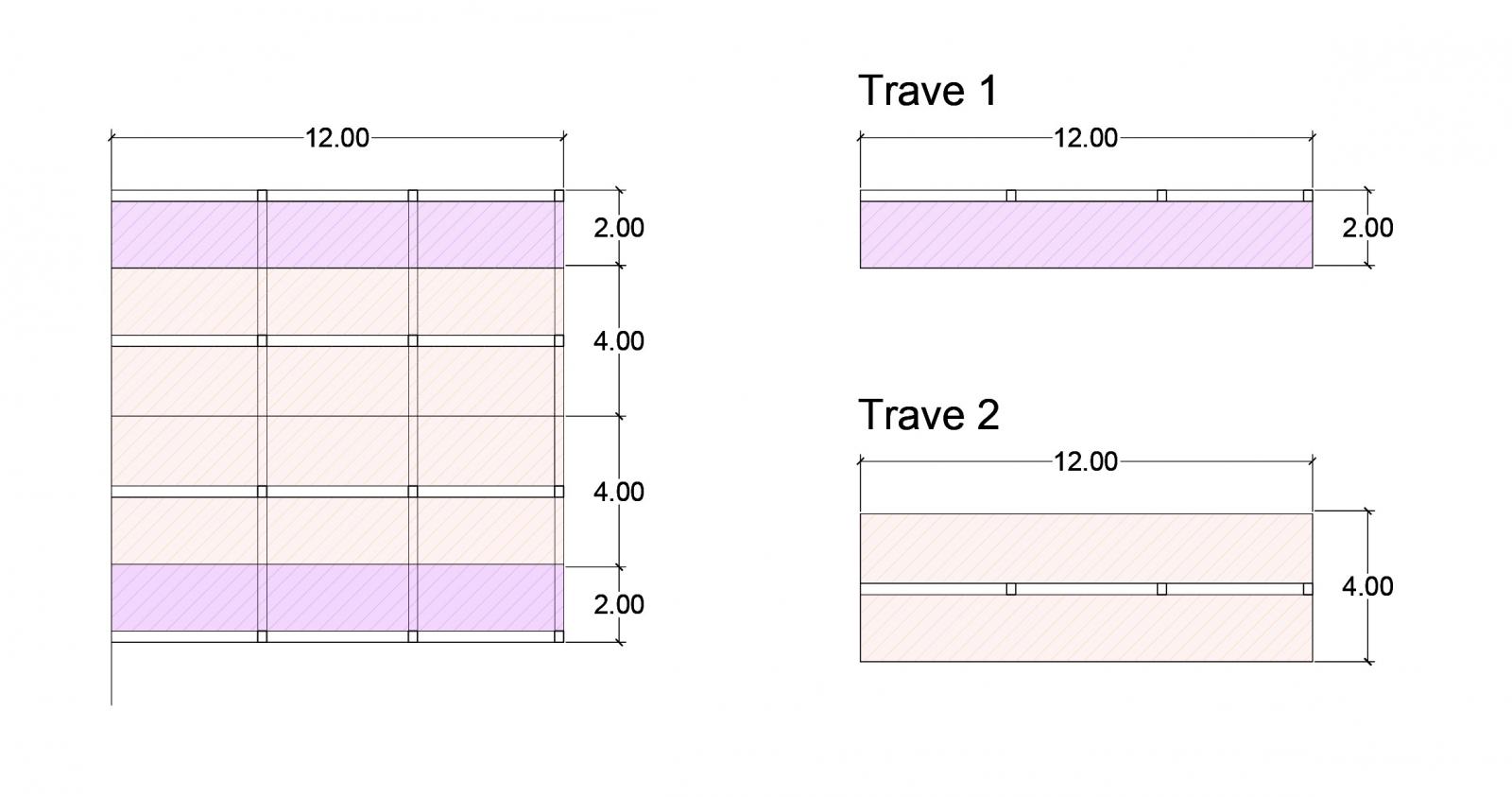
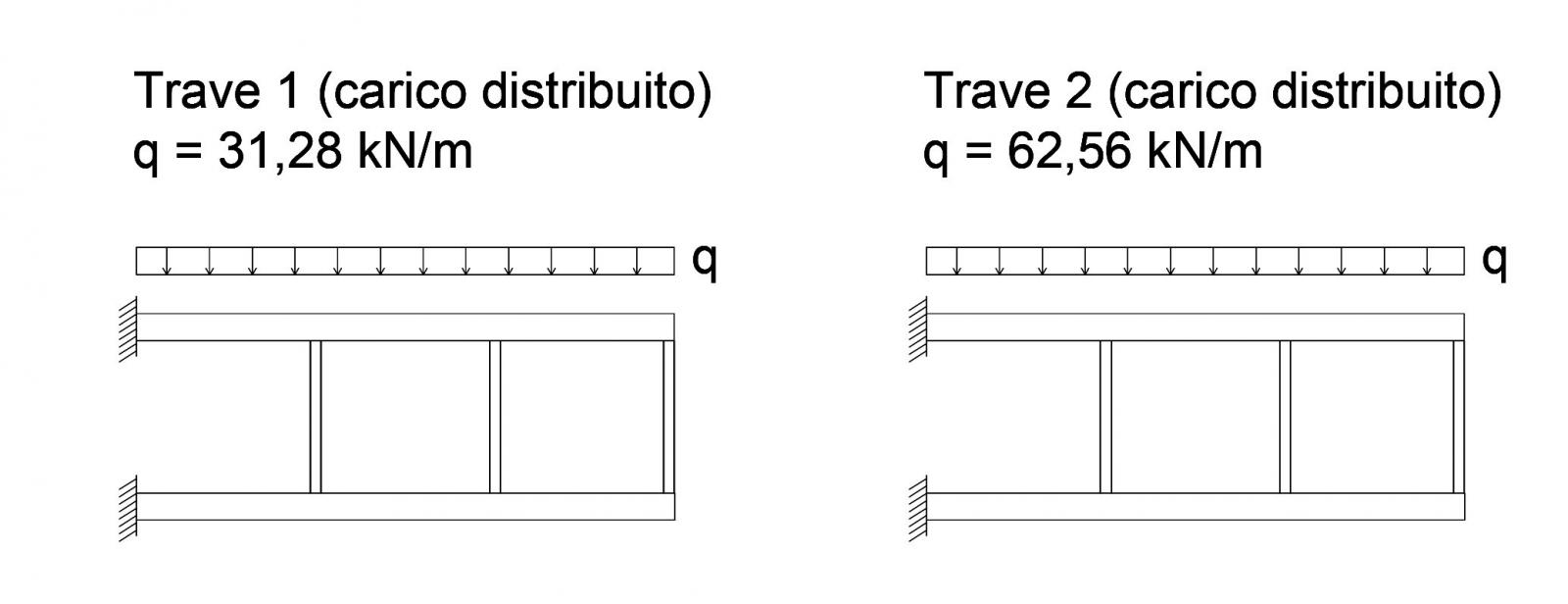
SLU trave1 : (1,3 x qs + 1,5 x qp + 1,5 x qa) x 2m = 31,28 kN/m
SLU trave2 : (1,3 x qs + 1,5 x qp + 1,5 x qa) x 4m = 62,56 kN/m
Area di influenza dei pilastri
Si possono dunque distinguere cinque casi.

SLU pilastro1 : (1,3 x qs + 1,5 x qp + 1,5 x qa) x 12mq = 187,68 kN
SLU pilastro2 : (1,3 x qs + 1,5 x qp + 1,5 x qa) x 8mq = 125,12 kN
SLU pilastro3 : (1,3 x qs + 1,5 x qp + 1,5 x qa) x 4mq = 62,56 kN
SLU pilastro4 : (1,3 x qs + 1,5 x qp + 1,5 x qa) x 24mq = 375,36 kN
SLU pilastro5 : (1,3 x qs + 1,5 x qp + 1,5 x qa) x 16m = 250,24 kN
4.Dimensionamento e definizione del modello su SAP2000 :
Una volta definita la configurazione della struttura e i carichi possiamo definire il modello su SAP. Utilizziamo le stesse sezioni usate nella seconda e terza esercitazione essendo sia la configurazione che i carichi molto simili a questa.
- Travi principali con una sezione 30x60 cm
-Travi secondarie con una sezione 25x35 cm
-Pilastri piano terra 55x55 cm
-Pilastri piano primo 45x45 cm
-Pilastri piano secondo 35x35 cm
-Pilastri piano terzo 25x25 cm
-Pilastri trave Vierendeel 30x60 cm

Per collegare le travi Vierendeel al setto utilizziamo lo strumento “Body”.
Dal momento che si tratta di una struttura internamente iperstatica, per risolverla dobbiamo considerare i montati infinitamente rigidi impedendo qualsiasi tipo di deformazione. In questo modo i collegamenti verticali non possono far altro che traslare verticalmente imprimendo una deformazione nei correnti orizzontali. Per rendere infinitamente rigidi i montanti della trave su SAP modifichiamo il momento di inerzia ponendolo uguale a un numero molto grande.
5.Verifiche delle travi Vierendeel:
a.Verifica degli elementi orizzontali e verticali:
Dopo aver dimensionato gli elementi orizzontali e verticali di ogni trave Vierendeel si procede con la verifica di tali elementi tramite tabelle excel. Per i pilastri è stata effettuata una verifica a presso-flessione, per gli elementi orizzontali a flessione semplice
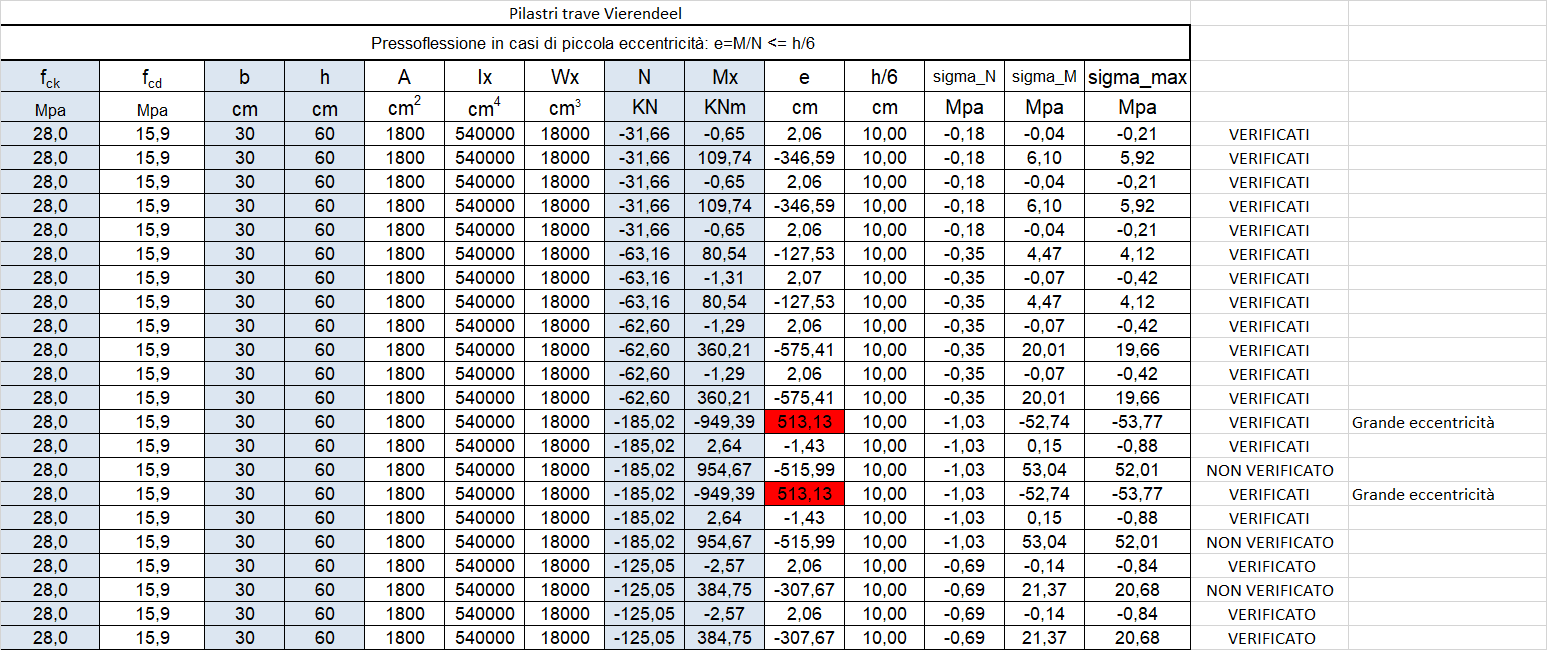
Per le travi e i pilastri che risultano non essere verificati, si procederà con un nuovo dimensionamento e una successiva verifica.
b.Verifica agli abbassamenti:
Dal modello SAP l’abbassamento verticale totale delle travi risulta essere:
U3 = 0,0211m
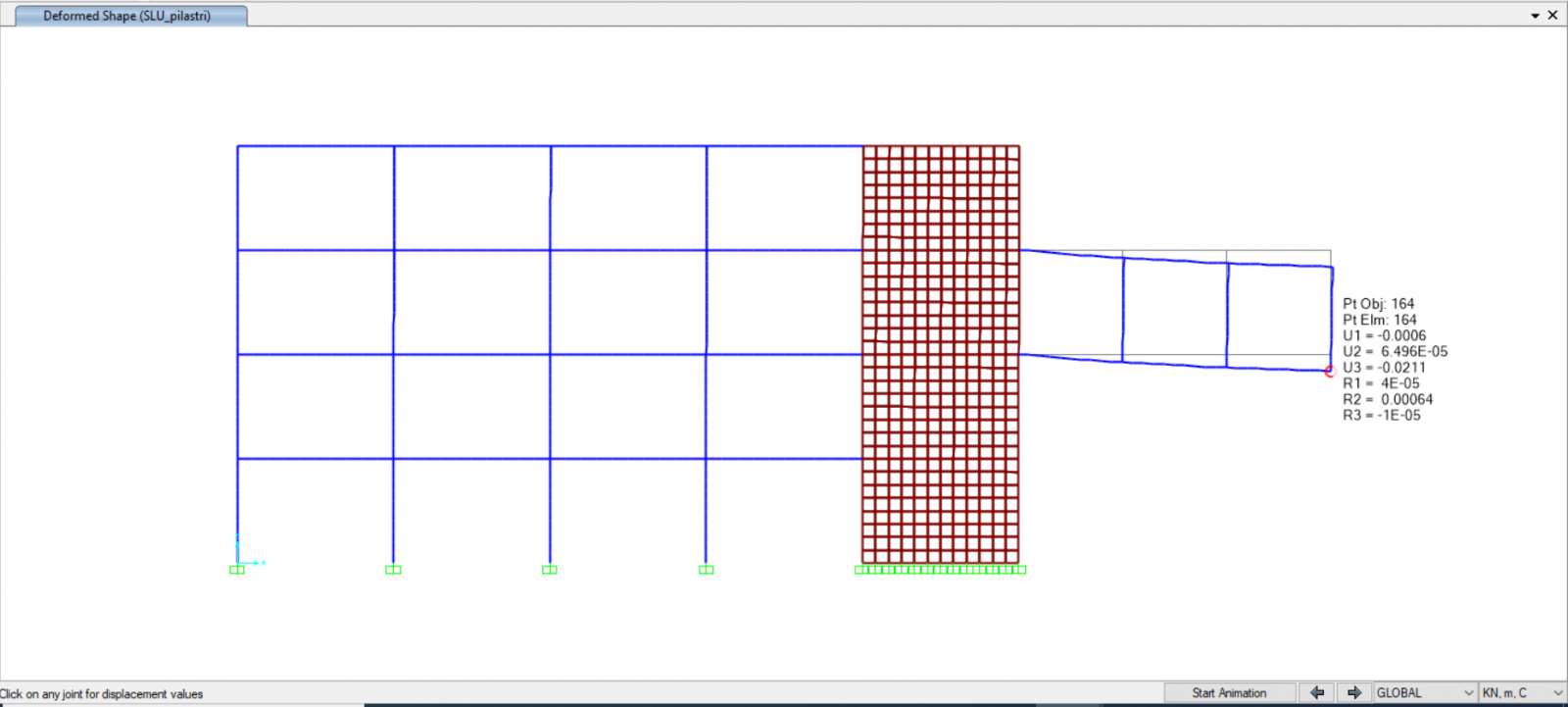
La verifica agli abbassamenti risulterà soddisfatta se:
U3 < Ltot/200
Sapendo che Ltot è la distanza dell’estremo libero dall’incastro, che nel nostro caso risulta essere 12m:
12/200 = 0,006 m
0,0471 m < 0,06 m Verifica soddisfatta
6.Analisi sollecitazioni:
Applicati i carichi avviamo l’analisi ed estraiamo i diagrammi di sforzo normale, taglio e momento.
Normale
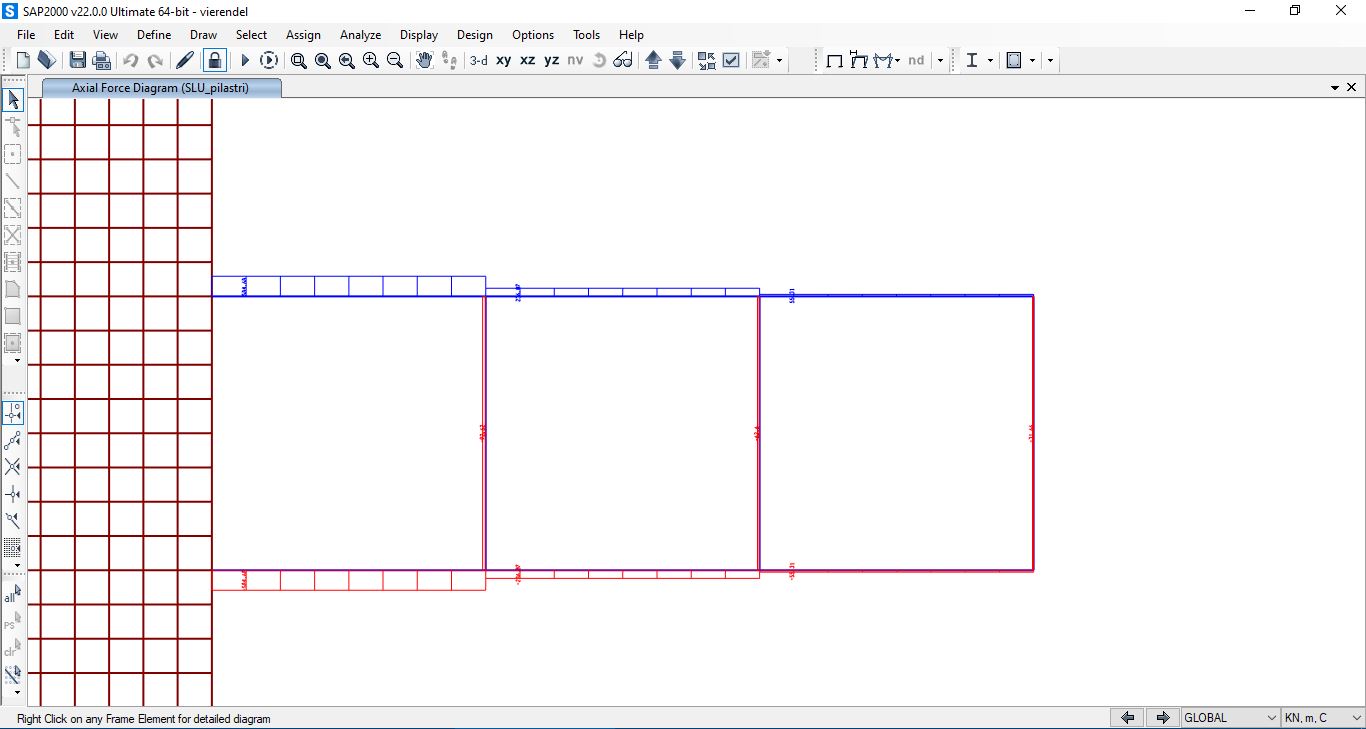
Taglio

Momento
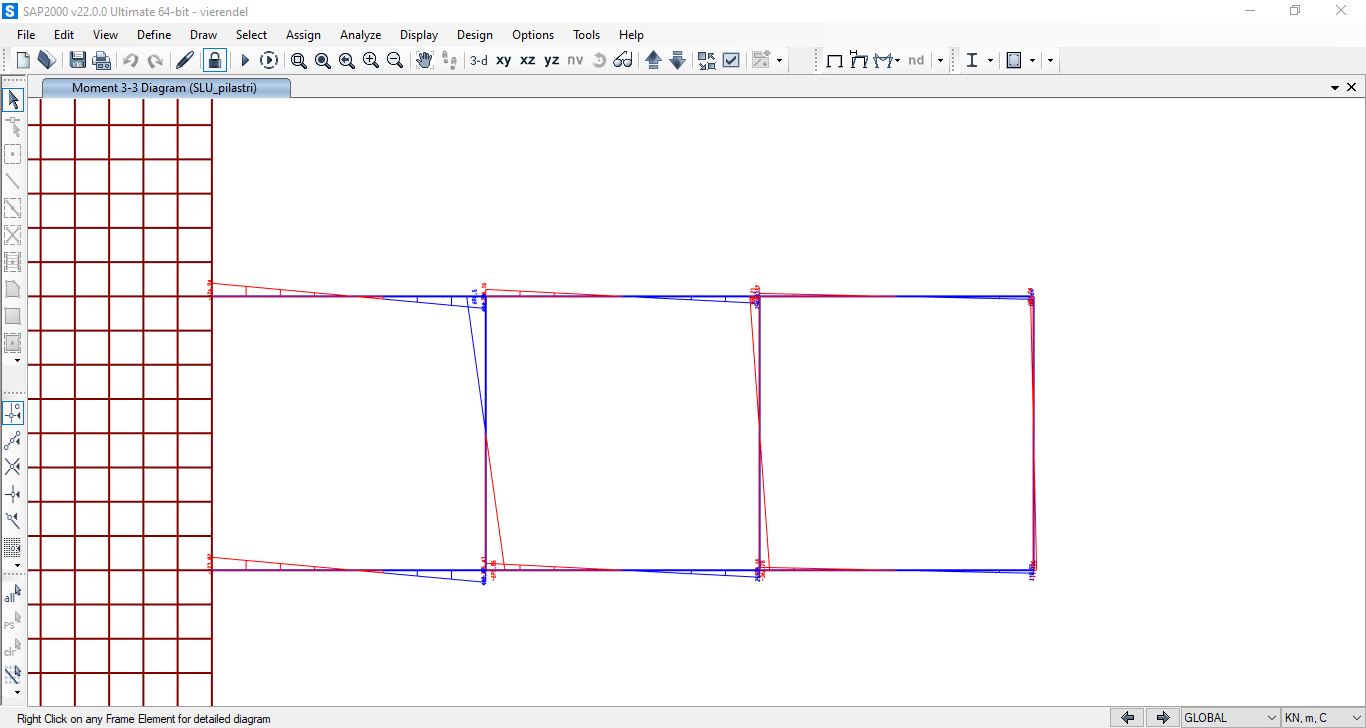
Prendiamo anche in considerazione gli sforzi agenti sul setto:
Fmax

Vmax

Mmax
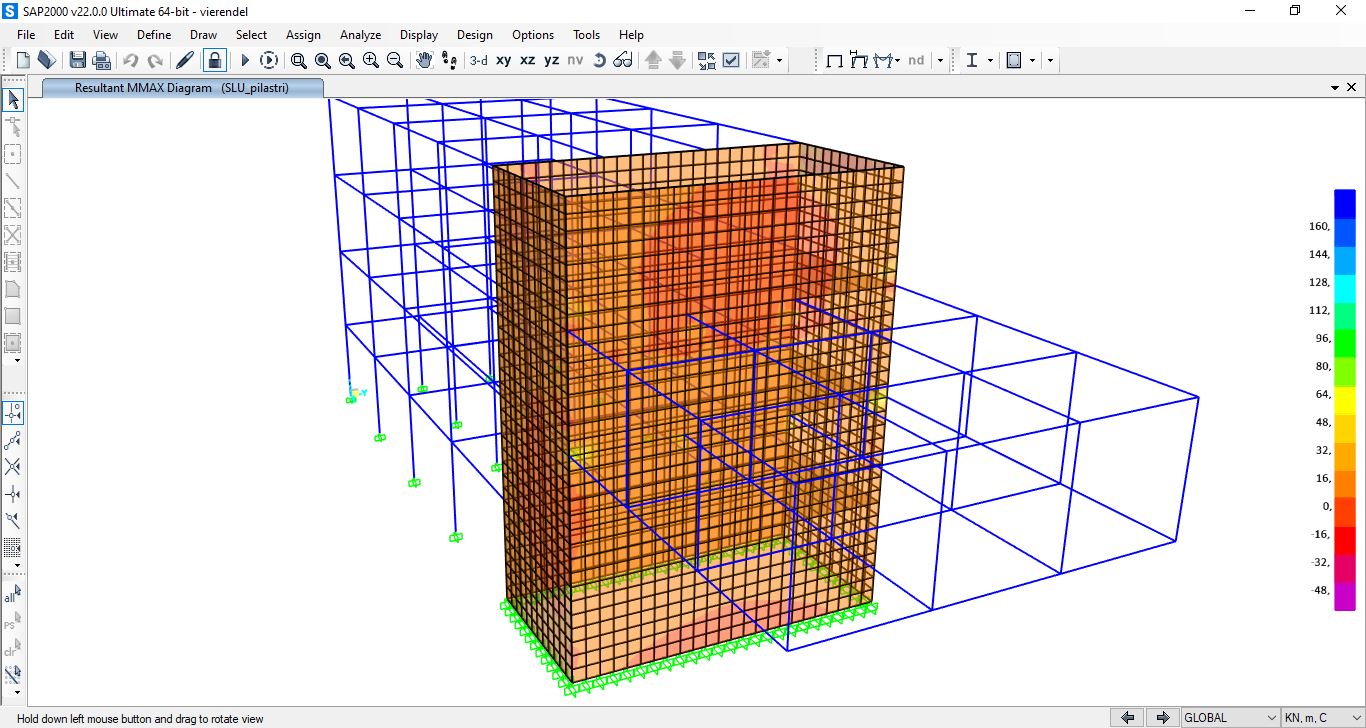
7.Conclusioni teoriche trave Vierendeel:
A livello teorico il comportamento di una trave Vierendeel può essere assimilato a quello di un telaio SHEAR TYPE ruotato di 90°, in questo caso si configura come una mensola, incastrato solo da un lato. Le caratteristiche principali di tale modello sono:
- l’infinita rigidezza degli elementi verticali (pilastri)
- nodi ad incastro tra elementi verticali ed orizzontali
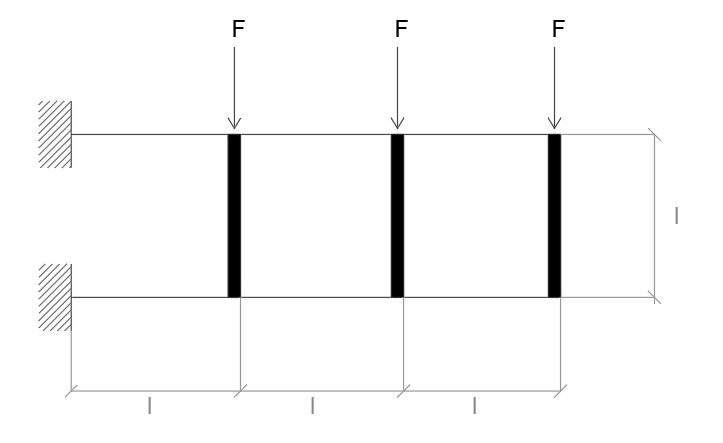
Applicando una forza F concentrata su ogni pilastro, il comportamento della trave si può assimilare agli schemi notevoli della trave doppiamente appoggiata ovvero:
- La deformata caratterizzata da spostamenti (abbassamenti) δ
- Il valore del diagramma del taglio costante
- Il valore del diagramma del momento lineare
La relazione tra F e spostamento è descritta in questo modo:
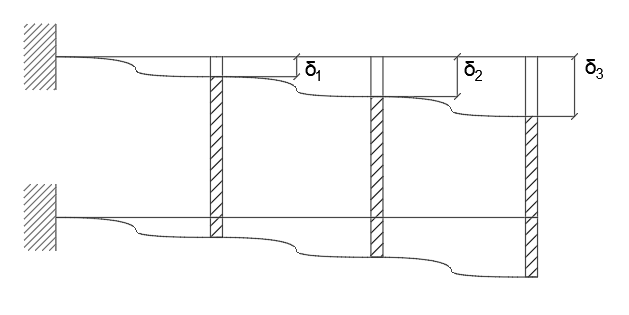
con k=rigidezza dell’elemento
Per trovare il valore del taglio e del momento di ogni asta orizzontale si considerano le seguenti relazioni:
M= 6EI/l²*δ T= 12 EI/l³*δ
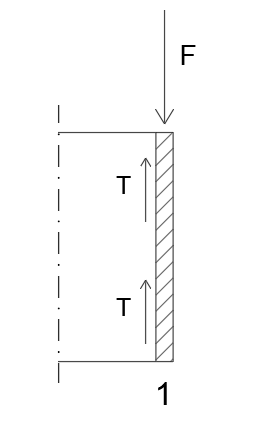
1. F = 2T → F = 24 EI/l³δ1
δ1= Fl³/24 EI
T = 12 EI/l³*δ1
M = 6 EI/l²*δ1
T = 12 EI/l³*(Fl³/24 EI) = F/2
M = 6 EI/l²*(Fl³/24 EI) = Fl/4
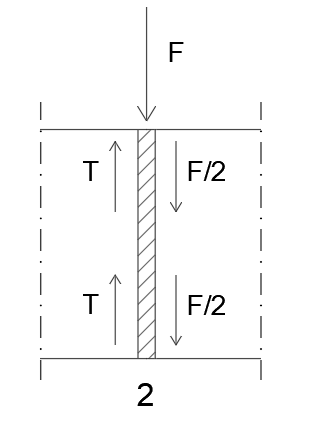
2. F + F/2 + F/2= 2T → 2F = 24 EI/l³*δ2
δ2= Fl³/12 EI
T = 12 EI/l³*δ2
M = 6 EI/l²*δ2
T = 12 EI/l³*(Fl³/12 EI) = F
M = 6 EI/l²*(Fl³/12 EI) = Fl/2
3. F + F + F= 2T → 3F = 24 EI/l³*δ3
δ3= Fl³/8 EI
T = 12 EI/l³*δ3
M = 6 EI/l²*δ3
T =12 EI/l³*(Fl³/8 EI) = 3/2F
M =6 EI/l²*(Fl³/8 EI) = 3/4 Fl
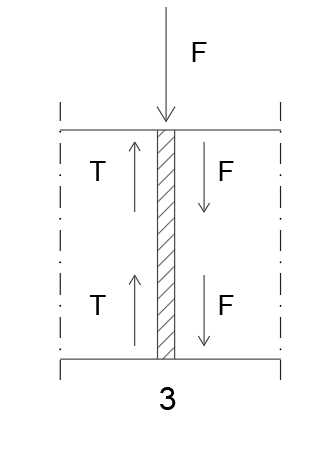
Diagramma dei valori del taglio elementi orizzontali:
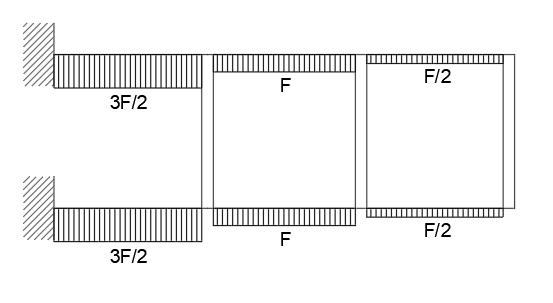
Diagramma dei valori del momento elementi orizzontali:
Per ricavare il valore del momento di ciascun elemento verticale si procede calcolando l’equilibrio di ogni nodo:
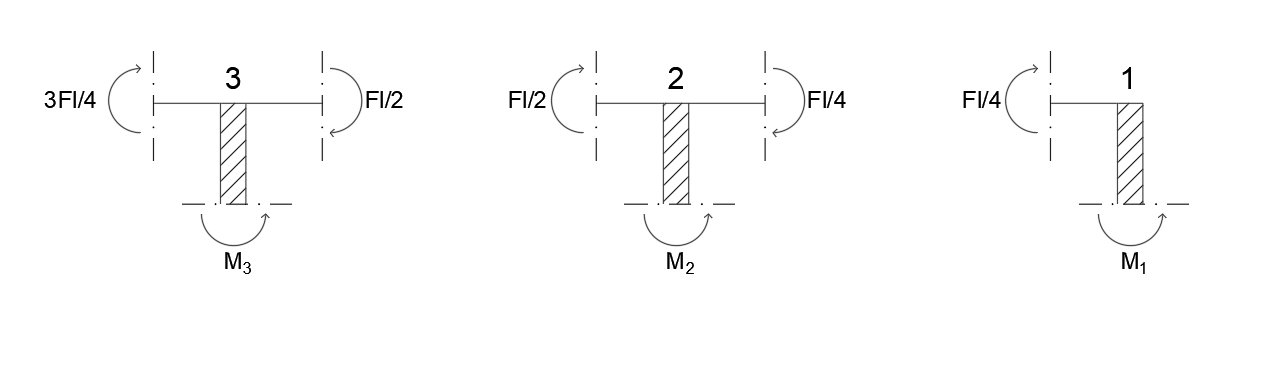
- M – Fl/4 = 0
M = Fl/4
- M – Fl/4 – Fl/2 = 0
M = 3/4Fl
- M – 3/4Fl – Fl/2 = 0
M = 5/4 Fl
Il valore del taglio si ricava dall’equilibrio di ogni asta verticale:
- T= (Fl/4 + Fl/4) 1/l = F/2
- T= (3/4Fl + 3/4Fl) 1/l = 3/2F
- T= (5/4Fl + 5/4Fl) 1/l = 5/2 F
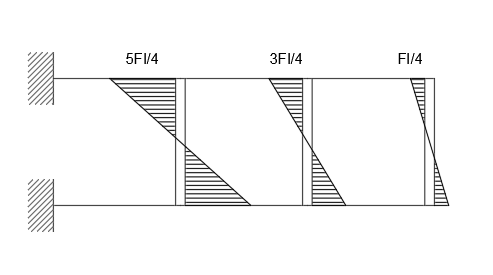
Diagramma dei valori del momento dei ritti:
Diagramma dei valori del taglio nei ritti:
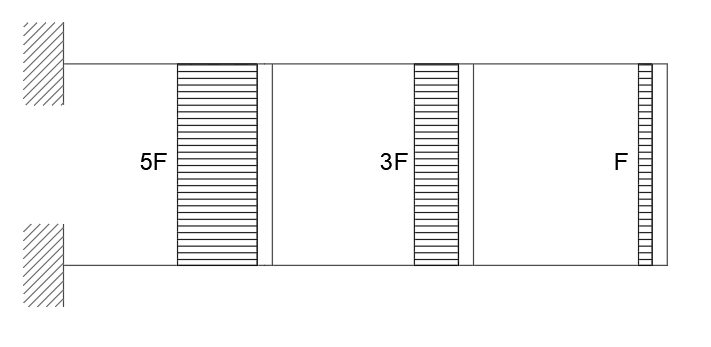
Per determinare i valori dello sforzo normale sui traversi si devono considerare i valori del taglio sui ritti che per gli elementi orizzontali si trasmettono come sollecitazione orizzontale:
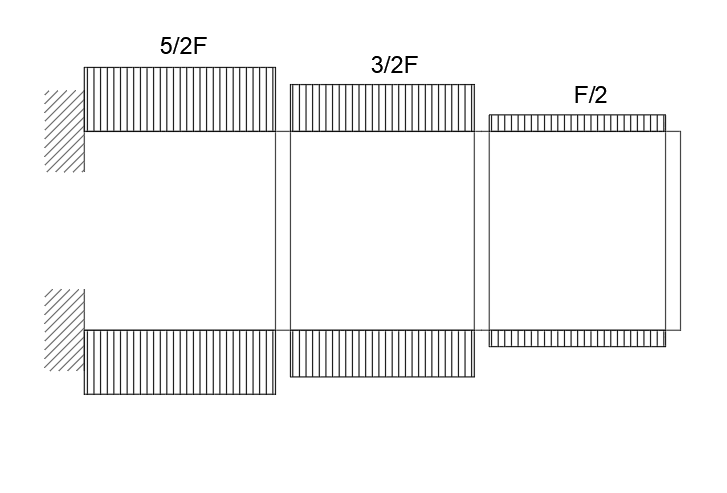
Commenti recenti