Esercitazione 5_ Dimensionamento e verifica di un graticcio di travi inflesse

Studentesse: Elena Santacesaria, Benedetta Schettini.

Definiamo le dimensioni del nostro graticcio: 12 m x 18 m.

Definiamo la sezione dei pilastri angolari e perimetrali, assegnandogli un valore rispettivamente di 0,8 x 0,8 m e di 0,8 x 0,5 m, e un calcestruzzo C50/60, disponendoli con un passo di 6 m.

Ruotiamo gli assi locali per posizionare correttamente i pilastri, ovvero in modo tale che il momento d’inerzia maggiore sia nella direzione del graticcio e definiamo i vincoli a terra come degli incastri.

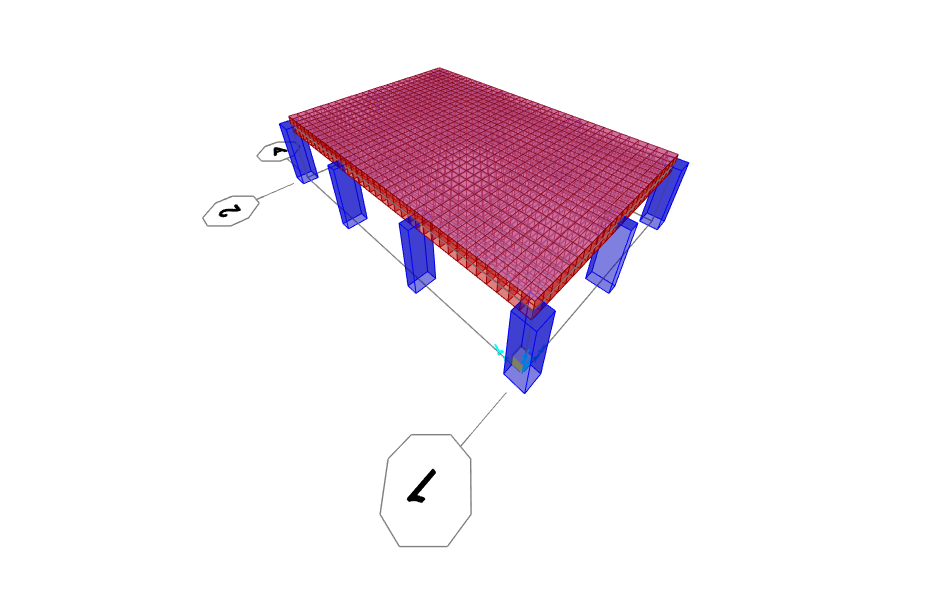
MODELLAZIONE SHELL

Modelliamo l’elemento shell con lo strumento _Drawpolyarea e ne discretizziamo la superficie.

Assegniamo alla shell uno spessore di 0,5 m e un materiale, il medesimo utilizzato per i pilastri, del quale abbiamo modificato il valore del coefficiente di Poisson ponendolo pari a zero in quanto utilizziamo un elemento continuo (shell) per simulare il comportamento di un elemento discontinuo (graticcio) nel quale le deformazioni laterali sono trascurabili e non hanno effetti secondari.

ANALISI DEI CARICHI (SHELL)

Ipotizziamo che sopra il graticcio gravi il peso di 4 piani. Calcoliamo un Qslu pari a 12,91 KN/mq.

Quindi definiamo un Load Pattern F con moltiplicatore pari a 1 (in quanto consideriamo il peso proprio del cls che non è trascurabile) e assegniamo i carichi ai nodi, secondo le rispettive aree di influenza.

Nodi centrali: 12,91 KN

Nodi perimetrali: 6,455 KN

Nodi angolari: 3,227 KN

Avviamo l’analisi. Da questa verifichiamo gli abbassamenti (accettabili poiché minori di 1/250 della luce) ed estrapoliamo il Momento massimo con il quale andiamo a verificare l’altezza minima della shell.

DIMENSIONAMENTO GRATICCIO

Tramite la tabella Excel verifichiamo che l’altezza assegnata alla shell non è sufficiente.

Quindi passiamo al dimensionamento del graticcio.

Per fare ciò procediamo con il calcolo del momento d’inerzia di una porzione di piastra che abbia una sezione di 0,5 m (altezza della piastra) x 2 m (che sarà il passo delle travi del graticcio). Ora ipotizziamo la base delle nostre travi (0,4 m), inserendola nella formula inversa dell’inerzia che abbiamo trovato. In questo modo, utilizziamo il valore del momento di inerza di un elemento con base 2m, per calcoare l'altezza minima di un elemento con base minore, ossia 0,4 m: la base delle travi del nostro graticcio.

Ipotizzando una base di 0,4 m, otteniamo un’altezza minima di 0,85 m.

MODELLAZIONE GRATICCIO

Procediamo con la modellazione del graticcio, assegnando a tutte le travi la stessa sezione ricavata dalla tabella, sapendo che il graticcio è una struttura agerarchica.

Imponiamo che all’intersezione di tutte le travi ci sia un nodo rigido, per fare ciò, dividiamo tutti i frame alle intersezioni con il comando edit_lines > divide_frames.

Creiamo un nuovo Load Pattern Q e assegniamo i carichi concentrati sui nodi in base alle aree di influenza.

Nodi centrali: 206,56 KN

Nodi perimetrali: 103,28 KN

Nodi angolari: 51,64 KN

Avviamo l’analisi, verifichiamo gli abbassamenti (che sono accettabili poiché minori di 1/250 della luce) e, inserendo nella tabella Excel il Momento massimo delle travi e dei pilastri, risultano verificate a flessione le travi centrali, mentre la sezione delle travi di bordo è sottodimensionata, per ciò che riguarda i pilastri risultano sottodimensionati anch'essi. Occorrerà dunque aumentarne le sezioni.

Diagramma Momento 3-3

  verifica pilastri perimetrali

verifica trave di bordo