DIMENSIONAMENTO DI UN GRATICCIO DI TRAVI INFLESSE_Lozonschi_Miloro

Per questa esercitazione abbiamo dimensionato un graticcio di travi inflesse partendo da un modello idealizzato di piastra, effettuando un infittimento delle travi. La piastra presenta un comportamento, fuori dal piano medio, soggetto prevalentemente a momento flettente M.

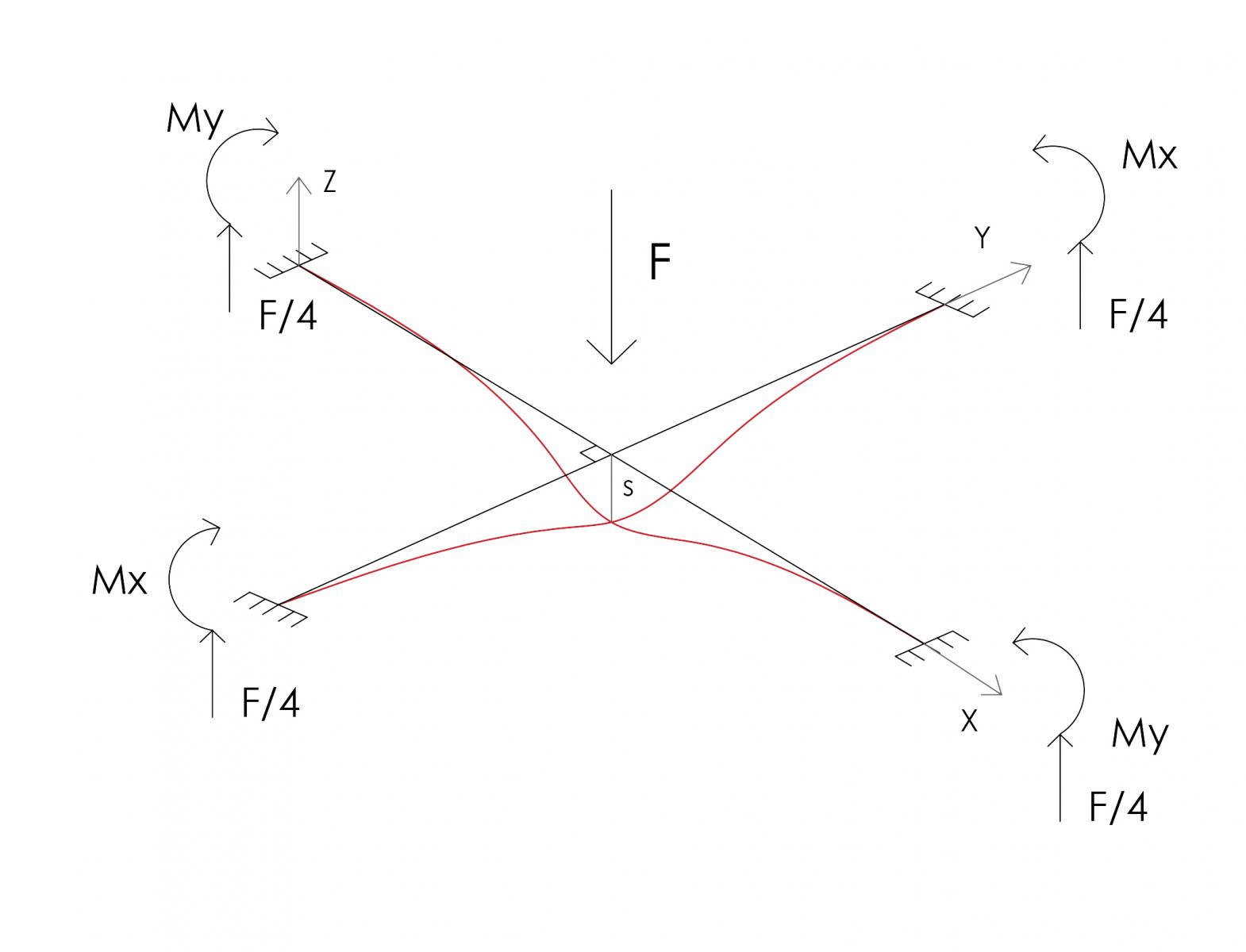
Momenti intorno a x e y.

Tagli che equilibrano la forza F.

Il graticcio è un oggetto tridimensioanle rappresentato da un modello bidimensionale dove i momenti abitano su due piani diversi per questo nell'equilibrio rotazionale si sommano i momenti Mx e My separatamente.

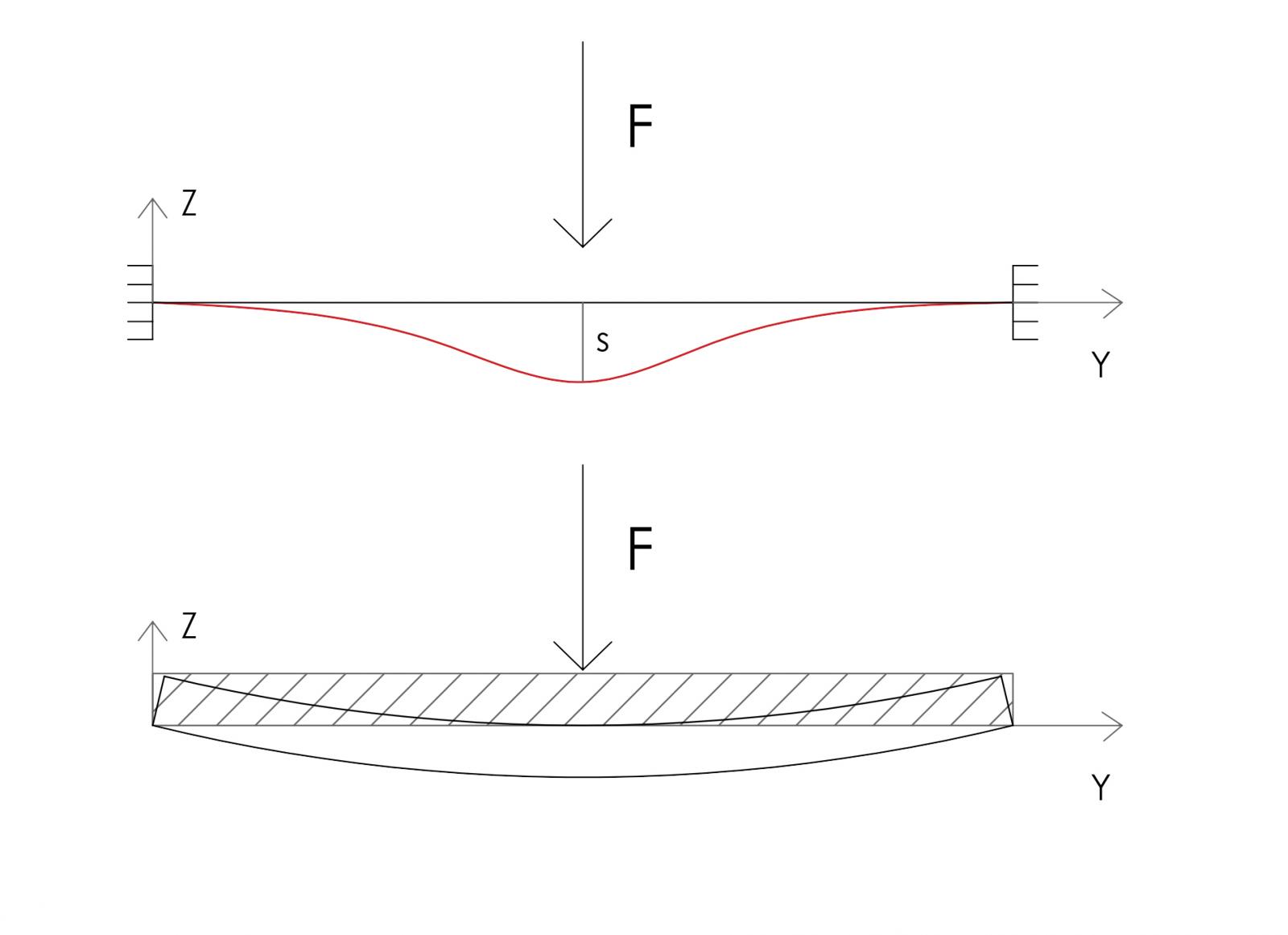
Rotazione e curvatura intorno a X

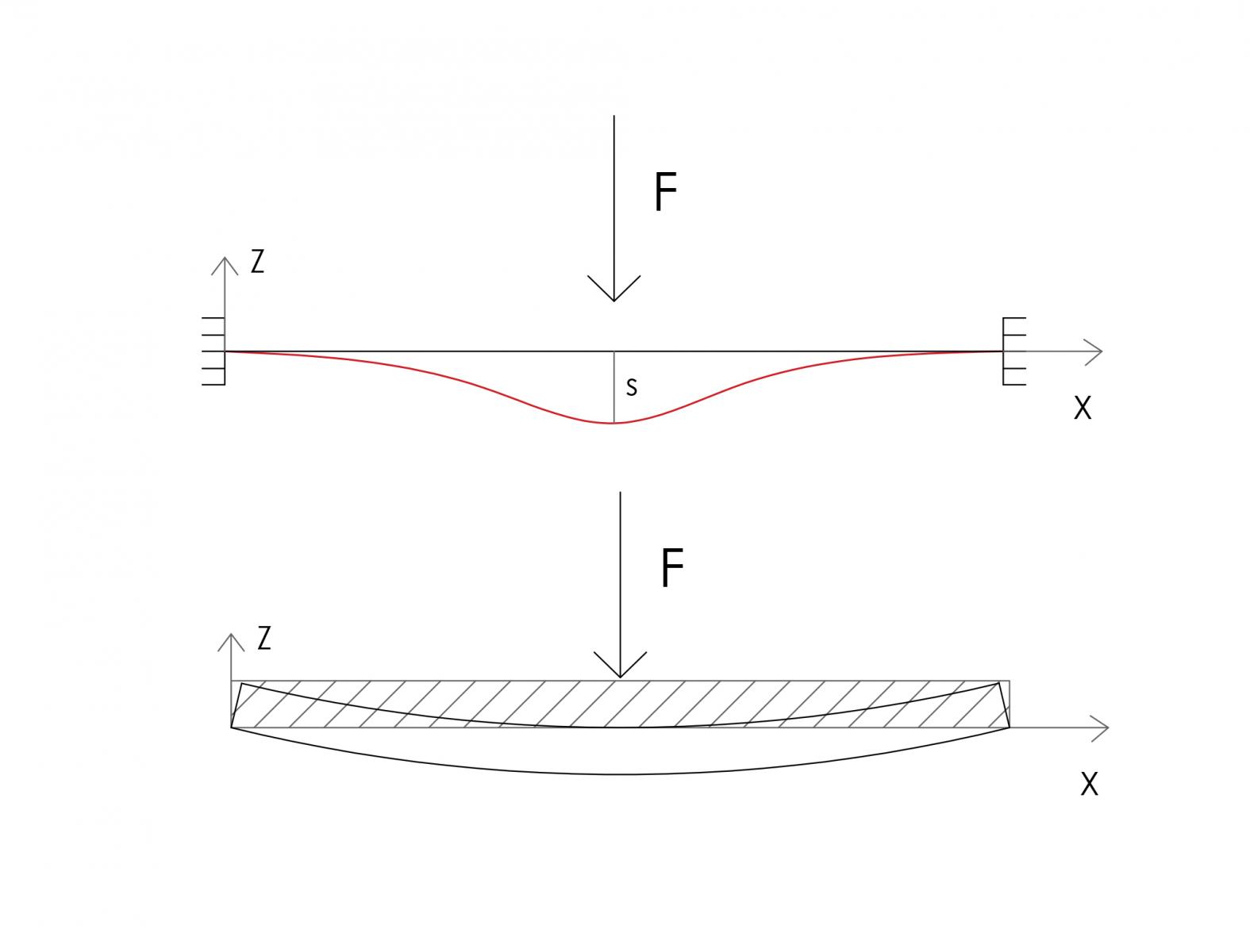
Rotazione e curvatura intorno a Y

GEOMETRIA

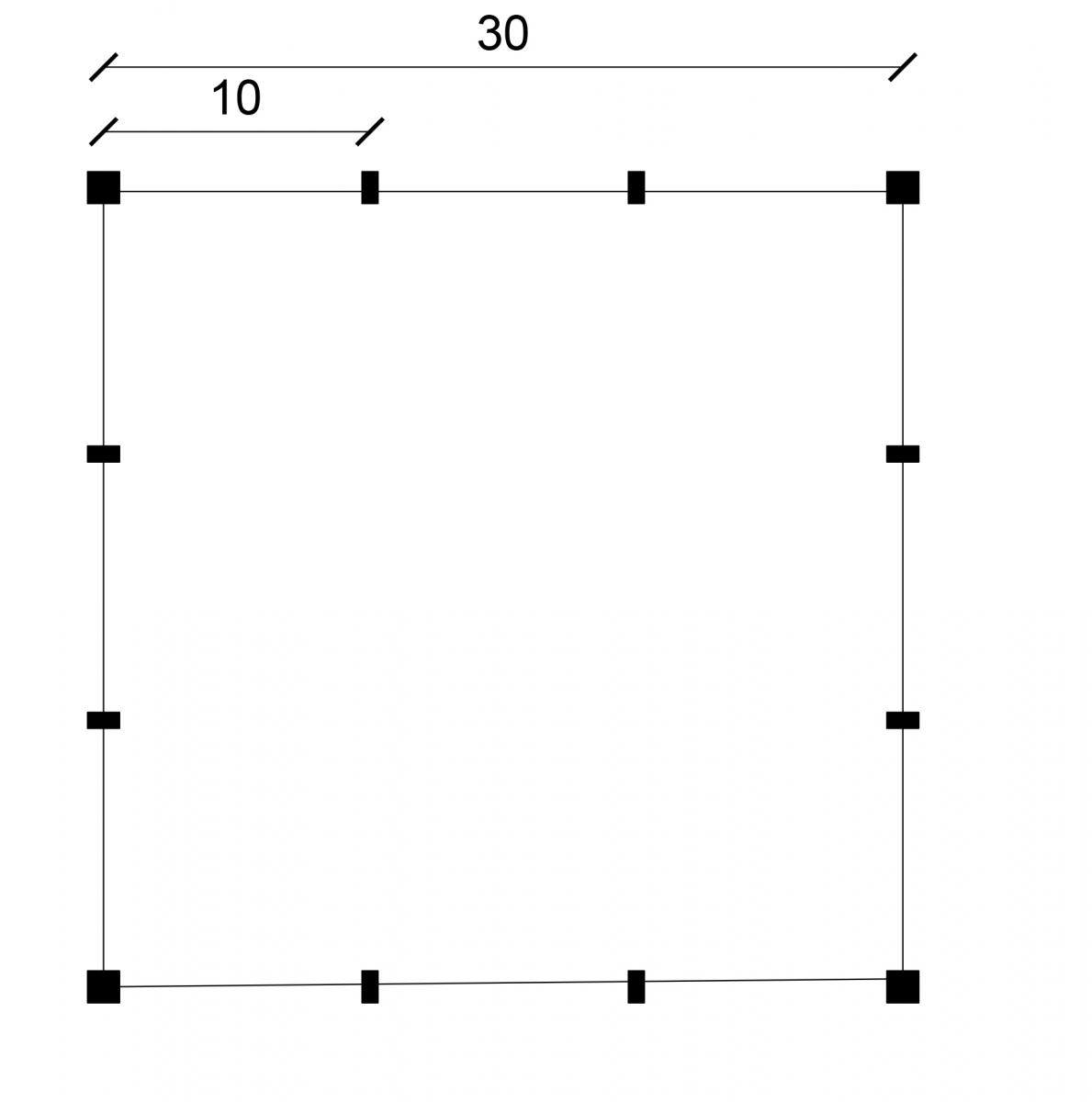
Abbiamo scelto una piastra di dimensioni 30 x 30 m con appoggi ogni 10 metri in modo da avere 4 appoggi per lato. a questo abbiamo diffrerenziato i pilastri per sezioni:

PILASTRI ANGOLARI: 100 x100 cm:

PILASTRI DI BORDO: 120 x 60 cm 

come prima cosa, avendo dimensionato sezioni rettangolari per i pilastri di bordo si dovrà tener conto dell’orientamentamento e quindi del valore del momento di inerzia che inciderà sulla rigidezza. Si è provveduto a ruotare i pilastri perimetrali posti lungo l’asse Y ( sistema globale ) andando a ruotare di 90° gli assi locali degli elementi. In questo modo il momento d’inerzia aumenta in quanto la base e l’altezza sono invertite e di conseguenza maggiore sarà la rigidezza.

Una volta assegnate le sezioni ai pilastri definiamo la sezione della piastra con shell-thick e imposto un’altezza di 100 cm. Per simulare il comportamento di un sistema discreto definisco un materiale C50/60 fittizio ponendo il coefficiente di poisson pari a 0 in quanto sappiamo che nel graticcio le deformazioni laterali delle travi sono trascurabili rispetto alle deformazioni principali.

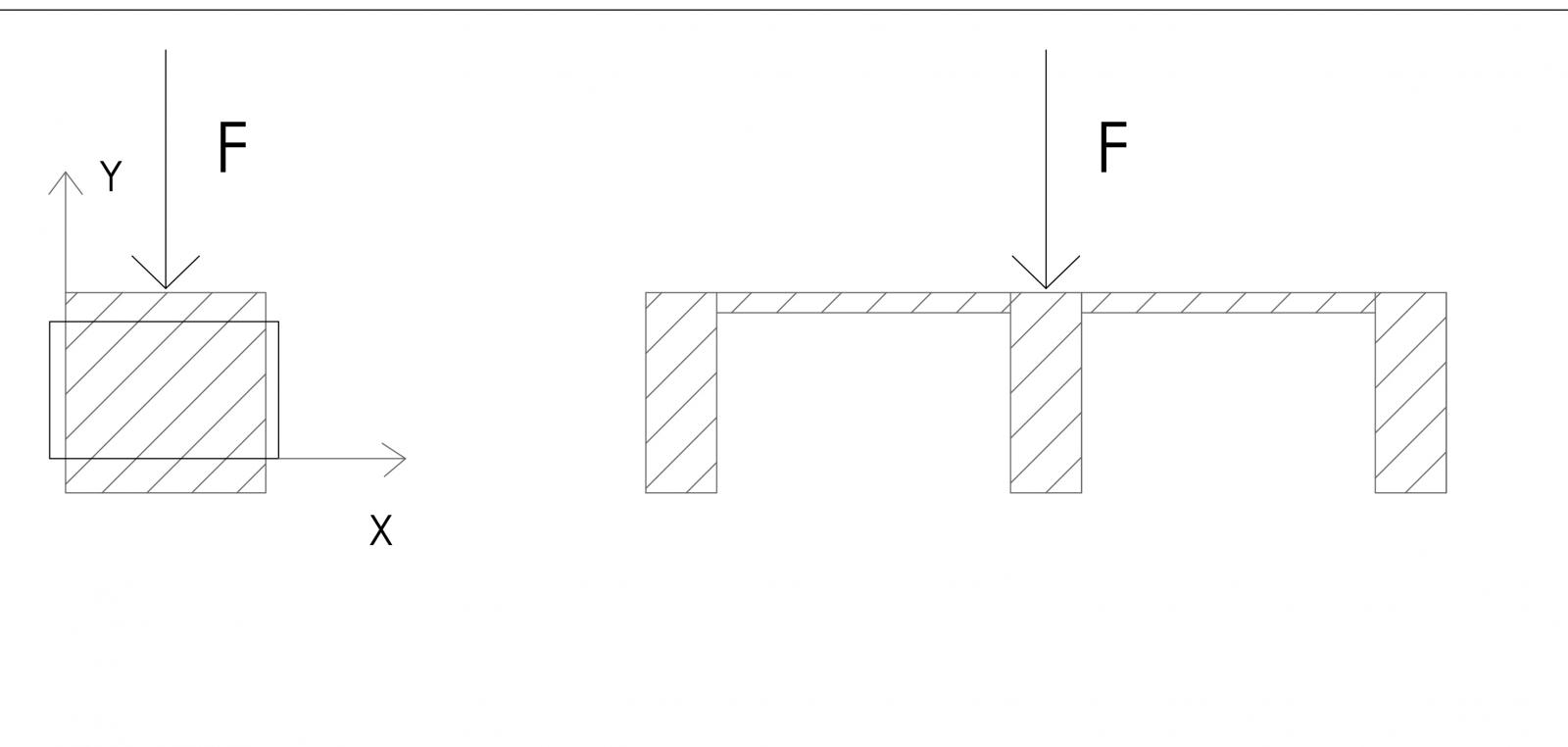
Sistema continuo; Sistema discontinuo

ASSEGNAZIONE DEI CARICHI

Dopo aver discretizzato l’area suddivido i nodi dell piastra per l’assegnazione dei carichi verticali:

NODI CENTRALI

NODI PERIMETRALI

NODI ANGOLARI

L’edificio ipotizzato ha una struttura che regge 4 piani. Ogni piano occupa una superficie di 900 mq. Devo calcolare il carico di stato ultimo qu facendo l’analisi dei carichi del solaio. Scelgo un solaio in acciaio con qu di 12,45 KN/m2 . Per ogni nodo viene considerata l’area di influenza, dove per i perimetrali l’area di influenza è la metà e per gli angolari è 1/4 mentre per quelli centrali è massima.

P solaio= n x qu x A = 4 x 12,45 KN/m2 x 900 m2 = 44820 KN 

Nodi totali - nodi perimetrali - nodi angolari = Nodi centrali = 3600

Fc= 44820 KN / 3600 = 12,45 KN

Fp= 12,45 KN / 2 = 6,22 KN

Fa= 6,22 KN / 2= 3,11 KN

Assegno le forze ai nodi e mando l’analisi con il carico definito allo SLU e con il fattore moltiplicativo a 1 per considerare il peso proprio della struttura. Dai diagrammi del momento flettente i valori di m 1-1 e m 2-2 sono gli stessi valori, in quanto il sistema è simmetrico. Prendiamo il valore massimo in corrispondenza di un pilastro per dimensionare l’altezza della piastra.

DISEGNO RETICOLO GRATICCIO

Per dimensionare l’altezza delle travi del graticcio abbiamo calcolato il momento di inerzia di una porzione di piastra considerando l’interasse delle travi quindi in base a quante travi posiziono lungo i lati. Le travi dovranno avere lo stesso lo stesso momento di inerzia della porzione di piastra ma con base un base diversa e l’altezza mi dovrà garantire lo stesso valore di I e quindi l’incognita è h3.

h = (12 Ix / b) 1/3

La sezione della trave da assegnare nel modello di SAP è 40 cm x 190 cm. A questo punto modello il reticolo di travi inflesse andando a definire le sezioni ottenute. Per simulare un nodo rigido interno separo le travi modellate in modo che non siano continue.

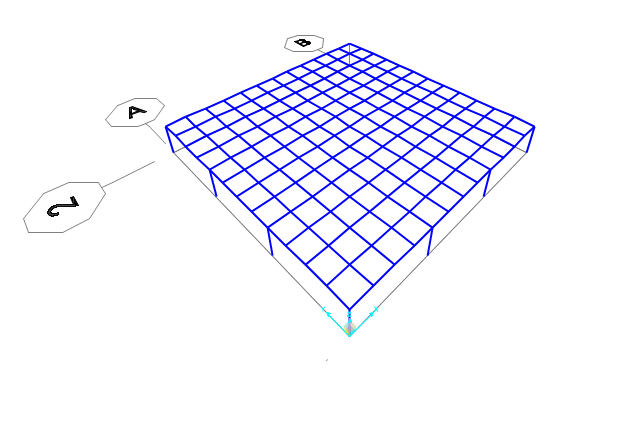
Vado ad assegnare le forze concentrate in corrispondenza dei nodi centrali, perimetrali e angolari considerando le relative aree di influenza.

Fc= 44820 m2 / 144 = 311,25 KN

Fp= 155,63 KN

Fa= 77,81 KN

Definisco un nuovo carico Q con fattore moltiplicativo pari ad 1 sempre per considerare il peso effettivo della struttura e mando l’analisi per effettura la verifica di resistenza degli elementi e verificare allo SLE gli abbassamenti.

VERIFICA DI RESISTENZA TRAVI

Confrontando i valori dei momenti, in corrispondenza del nodo rigido tra trave e appoggio notiamo che sono molto simili.

Mmax (trave) = 11343,30KNm

Mmax (pilastro) = 11935,94 KNm

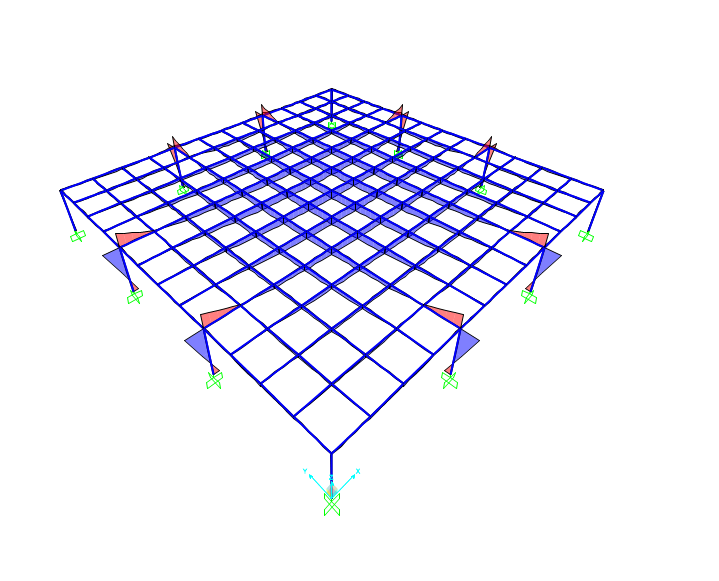
Diagrammi dei momenti M3 travi e pilastri

Per evitare che le travi si deformino troppo possiamo aumentare la rigidezza torsionale della trave di bordo, in questo modo, parte del momento flettente che arriva al nodo sarà assorbito dalla trave di bordo irrigidita aumentando la base. Assegnata la nuova sezione alla trave di bordo di 100 x 190 cm rimandiamo l’analisi per verificare i momenti sulle travi del graticcio. Dato che i contributi dei momenti delle travi, che appoggiano sulla trave di bordo e sugli appoggi scaricheranno sui pilastri, quest’ultimi risulteranno molto sollecitati. Dimensiono la sezione dei pilastri con il momento massimo 11351,11 KNm.

la sezione da assegnare ai pilastri è 60 x 190 cm. A questo punto per dimensionare la sezione della trave del graticcio rimando l’analisi prendendo il nuovo valore del momento massimo uguale 11247,83 KNm.

L’altezza minima risulta essere 219,78 cm quindi posso prendere una sezione di 40 cm x 230 cm e la assegno su SAP. Rimandando nuovamente l’analisi, il valore del momento massimo risulta 11562,35 KNm.

La sezione 40 x 230 cm risulta soddisfatta per la verifica a resistenza.

VERIFICA A PRESSOFLESSIONE PILASTRI

A questo punto abbiamo verificato la sezione dei pilastri soggetti a pressoflessione con il valore del momento ottenuto dopo aver assegnato la sezione della trave di bordo. Possiamo notare dal diagramma dello sforzo normale che il graticcio si comporta come una serie di portali.

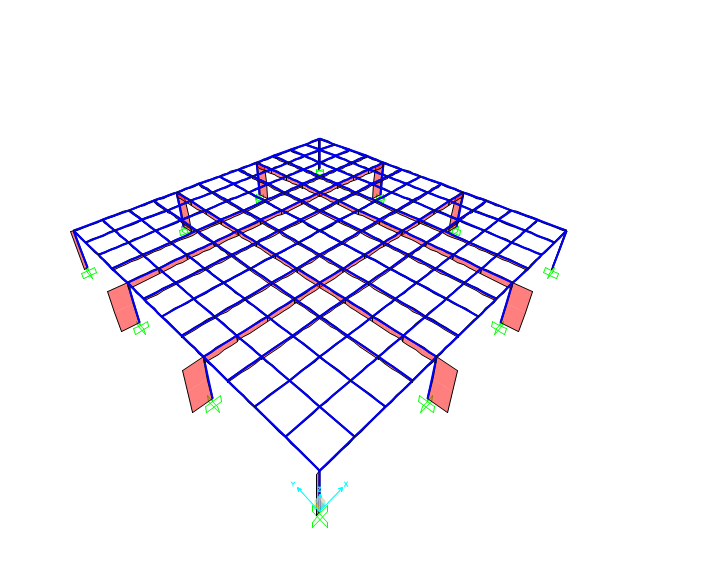
Diagrammi Sforzo normale

 Dalla verifica risulta non verificata la sezione 60 x 190 cm e quindi andremo ad aumentare la sezione ottenendo dei piccoli setti.

VERIFICA DEFORMABILITA'

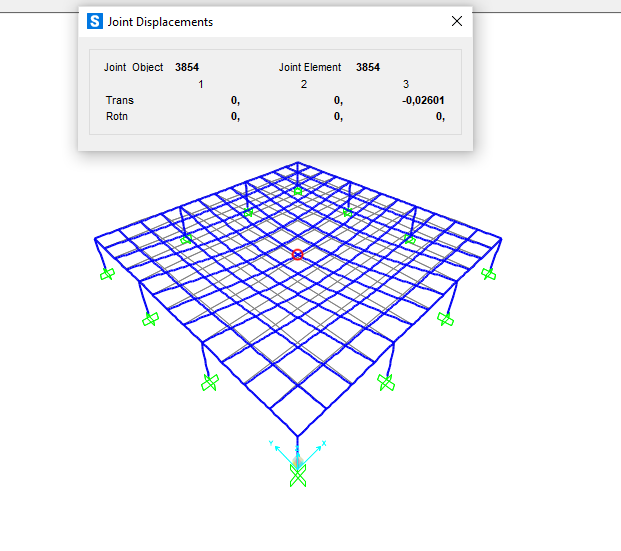
Devo verificare di quanto si abbassi e per essere soddisfatta l’abbassamento maggiore non deve superare un 1/200 della distanza maggiore tra gli appoggi. Per verificare la deformabilità devo assegnare il carico allo stato limite d’esercizio. Prendo lo spostamento maggiore e verifico che sia minore di L/200, dove L è la distanza massima. Dalla deformata risulta che il valore massimo di abbassamento è di 2,6 cm che soddisfa la verifica di deformabilità.