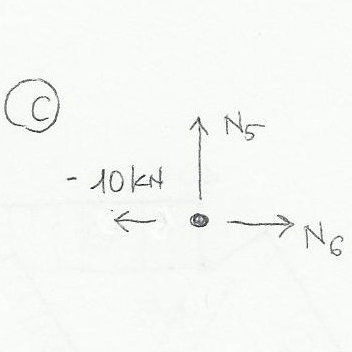
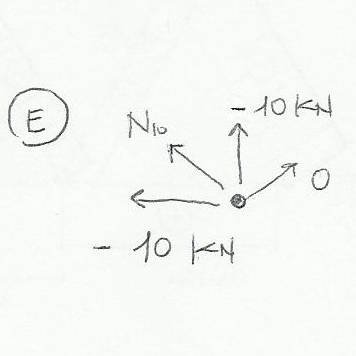
Prima di procedere al calcolo delle reazioni vincolari e delle azioni di contatto è fondamentale verificare l’isostaticità della struttura ovvero:
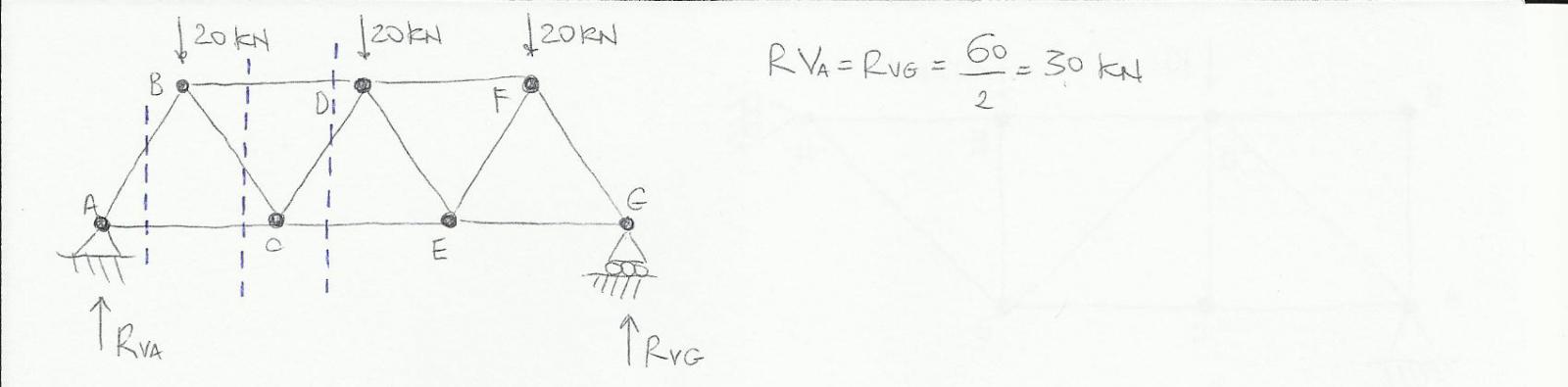
Ora si può procedere al calcolo delle reazioni vincolari e delle azioni di contatto.
Essendo una struttura simmetrica sottoposta a soli carichi verticali le reazioni vincolari sono di uguale intensità e corrispondono a 30 KN.
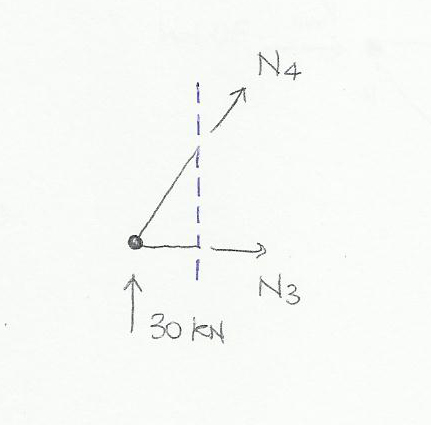
Calcolate le reazioni vincolari si può procedere al taglio delle varie aste per trovare le azioni di contatto facendo attenzione a tagliare 3 aste che non convergono ad uno stesso punto.
Per le aste oblique è fondamentale scomporre la forza nelle sue due componenti verticale ed orizzontale. In questo caso specifico un’asta inclinata di 45° ha due componenti di uguale valore pari a N x (radice di 2 su 2)
Essendo una struttura simmetrica i risultati trovati con sole 3 sezioni possono essere estese senza effettuare calcoli al resto della travatura.
DIMENSIONAMENTO DI UNA TRAVE
L’esercitazione prevede la progettazione di una trave in legno, acciaio e calcestruzzo mediante l’utilizzo del foglio excel.
Stabilito il telaio della struttura, ho deciso di analizzare la trave che deve sopportare il maggior carico ovvero la trave 2-3 lungo l’asse B.
TRAVE B 2-3 (trave doppiamente appoggiata)
-Interasse: 3 m
-Area di influenza: 12 mq
Nella progettazione di una trave bisogna calcolare la sommatoria di tutti i carichi previsti:
1. Carico strutturale: peso della struttura
2. Sovraccarico permanente: peso di elementi non strutturali che compongono il pacchetto del solaio
3. Sovraccarico accidentale: peso che dipende dalla funzione che ha un edificio o una sua parte. Immaginando l’edificio per civile abitazione possiamo stabilire il carico accidentale pari a 2 KN/mq
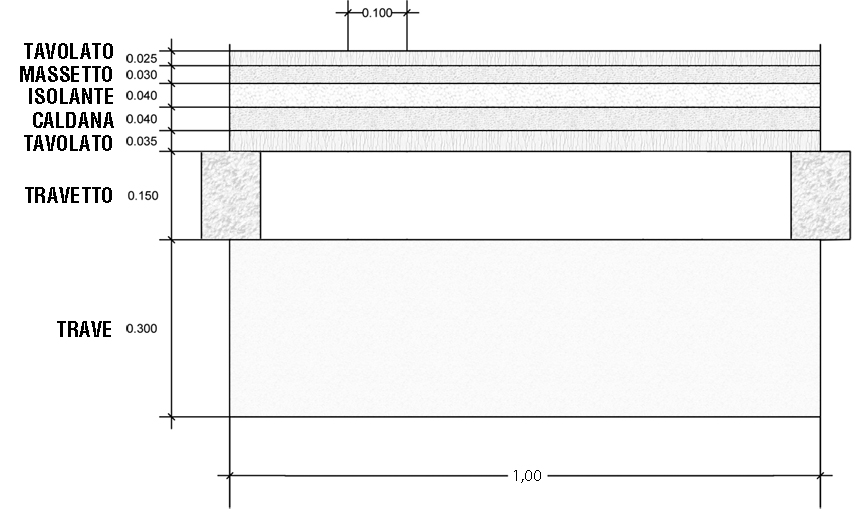
TRAVE IN LEGNO (massello)
Nel dimensionamento della trave principale bisogna considerare carico strutturale dei travetti. È importante quindi dimensionarli prima della trave principale per ottenere un calcolo più preciso.
Peso specifico del legno: tra i 5 e i 7 KN/mc. Prenderò il valore medio pari a 6 KN/mc = ɣ
DIMENSIONAMENTO DEI TRAVETTI: (interasse 1 m, luce 3 m)
1. Carico strutturale (qs):
· Tavolato in legno (spessore 0,035m):
P = V x ɣ =(1m x 1m x 0,035) x 6KN/mc = 0,21 KN
Qs= P/A = 0,21 KN / 1mq = 0,21 KN/mq
2. Sovraccarico permanente (qp): ɣ x h
· Tavolato in quercia (spessore 0,025m): 8KN/mc x 0,025m= 0,20 KN/mq
· Massetto in cls (spessore 0,03m): 20KN/mc x 0,03m= 0,60 KN/mq
· Isolante in fibra di legno (spessore 0,04m): 9KN/mc x 0,04m= 0,36 KN/mq
· Caldana (spessore 0,04m): 10KN/mc x 0,04m= 0,40 KN/mq
· Impianti 0,5 KN/mq
TOTALE qp = 0,20 + 0,60 + 0,36 +0,40 + 0,50 = 2,06KN/mq
3. Sovraccarico accidentale (qa): 2KN/mq
FOGLIO EXCEL (TRAVETTI)
1. Calcolo del carico totale a metro lineare:
(qs, qp, qa) x i = (0,21 KN/mc +2,06 KN/mc +2KN/mc) x 1m = 4,27KN/mc
2. Calcolo del momento massimo di una trave doppiamente appoggiata:
M= q x l2/8 = 4,27 KN/mc x (3mx3m)/8 = 4,80 KN*m
3. Calcolo della tensione di progetto fD:
fm,K x Kmod /1,45 = 28*0,5/1,45 = 9,66 N/mmq
in cui fm è la resistenza a flessione del legno, Kmod è un coefficiente in funzione della durata del carico nel tempo e ha valori compresi tra 0,3 e 0,5.
4. Calcolo dell’altezza del travetto stabilendo una base di 15 cm:
h = ((6 x M x 1000)/(b x fD))^0,5 =
14,11 cm
- un attraverso i risultati ottenuti si può ipotizzare travetto 15cm x 15cm
Nuovo calcolo aggiungendo il peso dei travetti al metro lineare totale:
qs + {(0,15m x 0,15m x 1m x 6 KN/mc)} = 0,21 KN/m + 0,135 KN/m = 0,345 KN/m

- anche aggiungendo il peso dei travetti ottengo un altezza pari a
14,33 cm e risulta dunque corretto il precedente dimensionamento
DIMENSIONAMENTO DELLA TRAVE : (interasse 3m, luce 4 m)
Anche per la trave si utilizza lo stesso procedimento
1. Carico strutturale (qs):
· Tavolato in legno (spessore 0,035m):
P = V x ɣ =(1m x 1m x 0,035) x 6KN/mc = 0,21 KN
qs= P/A = 0,21 KN / 1mq = 0,21 KN/mq
· Travetti (15 x 15 cm):
qs = 0,135 KN/mq
· qs TOTALE = 0,345 KN/mq
2. Sovraccarico permanente (qp): 2,06KN/mq
3. Sovraccarico accidentale (qa): 2KN/mq
FOGLIO EXCEL (TRAVE)
1. Calcolo del carico totale a metro lineare:
(qs, qp, qa) x i = (0,345 KN/mc +2,06 KN/mc +2KN/mc) x 3m = 13,21KN/mc
2. Calcolo del momento massimo di una trave doppiamente appoggiata:
M= q x l2/8 = 13,21 KN/mc x (4mx4m)/8 = 26,43 KN*m
3. Calcolo della tensione di progetto fD:
fm,K x Kmod /1,45 = 28*0,5/1,45 = 9,66 N/mmq
4. Calcolo dell’altezza del travetto stabilendo una base di 20 cm:
h = ((6 x M x 1000)/(b x fD))^0,5 =
28,66 cm
- attraverso i risultati ottenuti si può ipotizzare una trave di 20cm x 30cm
Nuovo calcolo aggiungendo il peso delle travi al metro lineare totale:
qs + {(0,20m x 0,30m x 4m x 6 KN/mc)/(4 x 3)} = 0,345 KN/mq + 0,12 KN/mq =
0,465 KN/mq

- anche aggiungendo il peso della trave ottengo un altezza pari a 29,04 cm e risulta dunque corretto il precedente dimensionamento
SOLAIO IN ACCIAIO
DIMENSIONAMENTO DEI TRAVETTI: (interasse 1m, luce 3 m)
2. Sovraccarico permanente (qp):ɣ x h
-
Tavolato in quercia (spessore 0,025m): 8KN/mc x 0,025m= 0,20 KN/mq
-
Massetto in cls (spessore 0,03m): 20KN/mc x 0,03m= 0,60 KN/mq
-
Isolante in fibra di legno (spessore 0,04m): 9KN/mc x 0,04m= 0,36 KN/mq
-
Impianti 0,5 KN/mq
TOTALE qp = 0,20 + 0,60 + 0,36 + 0,50 = 1,66KN/mq
3. Sovraccarico accidentale (qa): 2KN/mq
FOGLIO EXCEL (TRAVETTI)
1. Calcolo del carico totale a metro lineare:
(qs, qp, qa) x i = (2,5 KN/mc +1,66 KN/mc +2KN/mc) x 1m = 6,16 KN/mc
2. Calcolo del momento massimo di una trave doppiamente appoggiata:
M= q x l2/8 = 6,16 KN/mc x (3mx3m)/8 = 6,93 KN*m
3. Calcolo della tensione di progetto sig_am:
fy,K /1,15 = 275/1,15 = 239,13 N/mmq
in cui 275 è la tensione di rottura in Mpa
4. Calcolo del modulo di resistenza:
Wx = M/sig_am*1000= 6,93* 239,13 *1000 =
28,98 cm^3
- attraverso il risultato ottenuto si può scegliere una trave IPE 100 con dimensioni pari b=55mm e h=100 mm, Wx = 34,2 cm^3 e peso pari a 0,081 KN/m
Nuovo calcolo aggiungendo il peso dei travetti al metro lineare totale:
qs + {(0,081 KN/m)/1 m} = 2,50 KN/mq + 0,081 KN/mq = 2,581 KN/mq
Wx = 29,36 cm^3

- anche aggiungendo il peso dei travetti ottengo un risultato inferiore al Wx trovato in precedenza; la trave IPE 100 è ugualmente verificata
DIMENSIONAMENTO DELLA TRAVE : (interasse 3m, luce 4 m)
-
Carico strutturale (qs):
TOTALE: 2,581 KN/mq
2. Sovraccarico permanente (qp):1,66KN/mq
3. Sovraccarico accidentale (qa): 2KN/mq
FOGLIO EXCEL (TRAVE)
1. Calcolo del carico totale a metro lineare:
(qs, qp, qa) x i = (2,581 KN/mc +1,66 KN/mc +2KN/mc) x 3m = 18,723 KN/mc
2. Calcolo del momento massimo di una trave doppiamente appoggiata:
M= q x l2/8 = 18,723 KN/mc x (4mx4m)/8 = 37,446 KN*m
3. Calcolo della tensione di progetto sig_am:
fy,K /1,15 = 275/1,15 = 239,13 N/mmq
in cui 275 è la tensione di rottura in Mpa
4. Calcolo del modulo di resistenza:
Wx = M/sig_am*1000= 37,446/ 239,13*1000 =
156,59 cm^3
- attraverso il risultato ottenuto si può scegliere una trave IPE 200 con dimensioni pari b=100mm e h=200 mm, Wx = 194,0 cm^3 e peso pari a 0,224 KN/m
Nuovo calcolo aggiungendo il peso dei travetti al metro lineare totale:
qs + {(0,224 KN/m)/3 m interasse} = 2,581 KN/mq + 0,07 KN/mq = 2,65 KN/mq
Wx 158,32 cm^3

- anche aggiungendo il peso della trave ottengo un risultato inferiore al Wx trovato in precedenza; la trave IPE 200 è ugualmente verificata
SOLAIO IN CLS (interasse 3m , luce 4m)
1. Carico strutturale (qs):
Solaio in laterocemento (20 cm blocco + 5 cm soletta): 3,17 KN/mq (valore tabellato)
2. Sovraccarico permanente (qp):ɣ x h
-
Tavolato in quercia (spessore 0,025m): 8KN/mc x 0,025m= 0,20 KN/mq
-
Massetto in cls (spessore 0,03m): 20KN/mc x 0,03m= 0,60 KN/mq
-
Isolante in fibra di legno (spessore 0,04m): 9KN/mc x 0,04m= 0,36 KN/mq
-
Impianti 0,5 KN/mq
-
Intonaco 10KN/mc x 0,015m= 0,15 KN/mq
TOTALE qp = 0,20 + 0,60 + 0,36 + 0,50 + 0,15 = 1,81KN/mq
3. Sovraccarico accidentale (qa): 2KN/mq
FOGLIO EXCEL
1. Calcolo del carico totale a metro lineare:
(qs, qp, qa) x i = (3,17 KN/mc +1,81 KN/mc +2KN/mc) x 3m = 20,94 KN/mc
2. Calcolo del momento massimo di una trave doppiamente appoggiata:
M= q x l2/8 = 20,94 KN/mc x (4mx4m)/8 = 41,88 KN*m
3. Calcolo della tensione di progetto fd_f:
fy/1,15=450/1,15= 391,30 N/mmq
-acciaio B450C
Il valore di progetto della tensione dell’acciaio sarà pari al valore massimo della tensione fy diviso il coefficiente di sicurezza 1,15
4. Calcolo della tensione di progetto fd_c:
fck/1,75=40/1,75= 22,86 N/mmq
-calcestruzzo C40/50
Il valore di progetto della tensione del calcestruzzo sarà pari alla resistenza cilindrica fck diviso il coefficiente di sicurezza 1,75
5. Calcolo della sezione della trave
Stabilendo una sezione di base pari a 20 cm otterrò un altezza utile pari a 21,56 cm. L’altezza utile corrisponde alla distanza tra il lembo compresso del calcestruzzo e l’armatura tesa. Per trovare l’altezza totale della sezione (H) si sommerà l’altezza utile e il copriferro ( 5 cm)=
21,56 cm+5 cm= 26,56 cm
6. Considero una sezione 20 x 30
Dopo aver dimensionato la trave si può procedere ad un nuovo calcolo di qs considerando tutti gli elementi della sezione:
CARICO TOTALE q = 20,94 KN/m + 1,33 KN/m= 22,27 KN/m
Anche sommando il carico della trave la sezione ipotizzata (20 x 30 cm) viene ugualmente verificata.
STRUTTURA RETICOLARE SPAZIALE
L’esercitazione prevede il disegno e l’analisi di una struttura reticolare spaziale tramite l’utilizzo di AUTOCAD e SAP2000.
AUTOCAD
Mi creo innanzitutto un nuovo layer “aste” in modo tale che, importando la struttura in SAP, potrò assegnare al layer la funzione di frames.
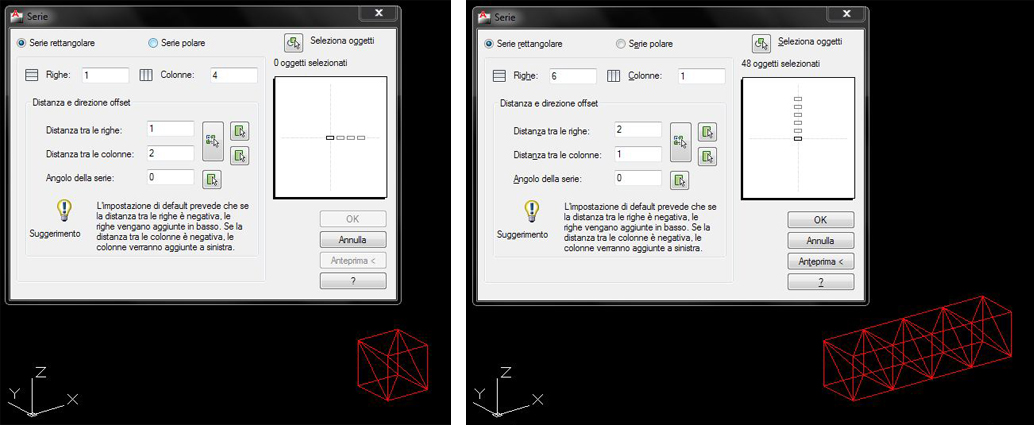
La struttura da analizzare, essendo modulare mi permette di realizzare un unico elemento da ripetere n volte nello spazio; con lo strumento polilinea e polilinea3D si parte quindi con il disegno di un modulo cubico (2m x 2m x 2m )completo di tutte e 6 le aste diagonali e posto in posizione 0,0,0
Ripeto dunque il modulo 4 volte lungo l’asse x e 6 volte lungo l’asse y tramite lo strumento array.
Completata la struttura, tramite il comando esplodi si dividono tutte le polilinee in linee in modo da avere tutte aste singole non legate fra loro.
La struttura però non è ancora del tutto corretta; con lo strumento overkill cancello tutte le aste che si sono sovrapposte le une sulle altre. Bisogna fare molta attenzione in questo passaggio poiché nel caso di sovrapposizioni avrei dei problemi nell’importazione in SAP.
Ecco la struttura completa e ripulita di tutte le sovrapposizioni.
Per importare correttamente il file su SAP salvo il file nell’estensione .dxf
SAP
Importo il file .dxf in SAP assegnando al layer “aste” la funzione frames.
Prima di procedere con il calcolo delle sollecitazioni è fondamentale eseguire una serie di operazioni:
-
Definizione dei vincoli esterni
-
Definizione dei vincoli interni
-
Definizione del materiale
-
Definizione della sezione
-
Definizione del carico
Definizione dei vincoli esterni
Si selezionano i 4 vertici inferiori della struttura e si assegna loro la funzione di cerniere.
Definizione dei vincoli interni
Tutte le aste della reticolare spaziale sono incernierate tra loro; è dunque importante imporre il rilascio del momento per ogni elemento. Per fare ciò basta seguire il percorso Select All > Assign > Frame > partial fixity > Assign frame releases e spuntare il rilascio del momento all’inizio e alla fine di ogni trave.
Definizione del materiale
È il momento di definire il materiale per la nostra struttura. Seguendo il percorso Define >material >New material" si può creare il materiale “acciaio”
Definizione della sezione
Per la definizione della sezione delle aste basta seguire il percorso Define >Section properties >frame section e selezionare il profilo tubolare. Nel creare una nuova sezione si deve assegnare ad esso il materiale “acciaio” appena creato.
Si può dunque selezionare tutte le aste della struttura e assegnare ad esse il profilo appena stabilito.
Definizione del carico
Si può ora stabilire un carico tramite Define >load pattern creando una “forza concentrata”. È ora necessario assegnare a tutti i nodi superiori della struttura la nostra forza concentrata; per selezionarli tutti ci si può porre nella vista xz o in una vista 3d e selezionare tutti i nodi superiori.
Ora si può assegnare facilmente ad ogni nodo un peso da noi stabilito; in questo caso simuleremo una forza di -40 Kn su ogni nodo.
La struttura ora è definita in ogni particolare e si può procedere all’analisi delle sollecitazioni andando ad osservare ovviamente tutti gli sforzi assiali presenti, di trazione e di compressione.
Per capire qual è l’asta più sollecitata si può seguire il percorso Display >Show Tables e selezionare Elements Output in cui si possono osservare tutte le caratteristiche e le sollecitazioni nelle varie aste ed individuare l'asta più sollecitata in trazione e compressione. Dopo averle individuate si può procedere al progetto e alla verifica a trazione e compressione delle aste più sollecitate.
SFORZO MASSIMO A COMPRESSIONE
L'asta più sollecitata a compressione è la numero 252 su cui agisce un N pari a 307,254 KN.
Scelgo un acciaio S355 e procedo al progetto della trave:
A = N / fd = 307,254 KN / (355/1,05) = 307254 N / (338,095 N/mmq) = 908,78 mmq = 9,09 cmq
consultando la tabella dei profili tubolari scelgo il profilo con una sezione di 10,70 cmq che più si avvicina al risultato ottenuto.
Il progetto della trave non è tuttavia terminato in quanto devo verificare, tramite la formula del carico critico euleriano, se la sezione è in grado di sopportare lo sforzo di compressione sottoposto:
Pcritico = (π2 * E * Jmin)/l02
in cui:
E= modulo di elasticità
Jmin= momento di inerzia: nel caso di profili tubolari è uguale in tutte le direzioni
l0= lunghezza libera di inflessione: in questo caso l'asta sottoposta a maggiore compressione è un'asta obliqua pari a 2,828 m; essendo un'asta doppiamente incernierata la lunghezza libera di inflessione è uguale alla lunghezza stessa dell'asta.
Pcritico = (3,14 * 3,14 *210000N/mmq * 963000 mm4)/ 2828 mm *2828 mm = 249313 N= 249,313 kN < 307,25 kN
L'asta non è verificata; scelgo il profilo immediatamente superiore con una sezione pari a 12,5 cmq e procedo nuovamente con i calcoli
Pcritico = (3,14 * 3,14 *210000N/mmq * 1920000 mm4)/ 2828 mm *2828 mm = 497,073 kN > 307,25 kN
l'asta è verificata.
SFORZO MASSIMO A TRAZIONE
Per il progetto a trazione il lavoro è più semplificato in quanto nn c'è bisogno di una verifica di instabilità; la trave più sollecitata a trazione è l'asta n.5 sottoposta a 258,934 KN.
Scelgo un acciaio S355 e procedo al progetto della trave:
A = N / fd = 258,934 KN / (355/1,05) = 258934 N / (338,095 N/mmq) = 766 mmq = 7,66 cmq
posso adottare il profilo gia precedentemente dimensionato con sezione pari a 12,5 cmq