TRAVE RETICOLARE SIMMETRICA

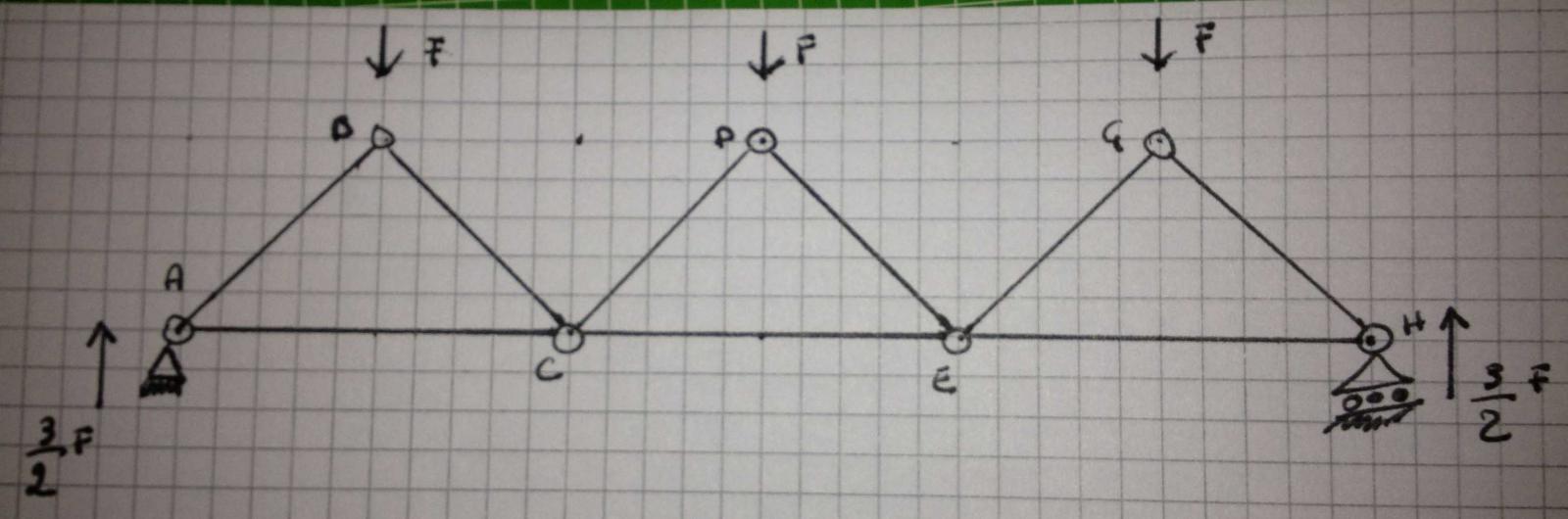
(la simmetricità della struttura ci permette di trovare subito le reazioni nei nodi esterni)

Verifico l'isostaticità: l=V

Ho a disposizione due metodi:

Per calcolare i gradi di libertà in ogni nodo: 2(n-1) dove n è il numero delle aste in quella cerniera! 

A-H=2     

B-G=4               ====> Vi= 2+2+4+4+6+6+6= 30

C-D-E=6

V=VE+Vi

VE=3 (vincoli esterni)

Vi=30(vincoli interni)

V=33 ======>   l=11x3=33 - V=3

l=V ISOSTATICA!

metodo alternativoetper verificare l'isostaticità: 

VE+a (aste) = 2xnodi

3+11=2x7 -------> 14=14 

Con questo metodo abbiamo verificato l'isostaticità, ma NON SAPPIAMO ogni nodo quanti gradi toglie.

Procedo sezionando la trave in corrispondenza di aste che convergono nello stesso nodo:

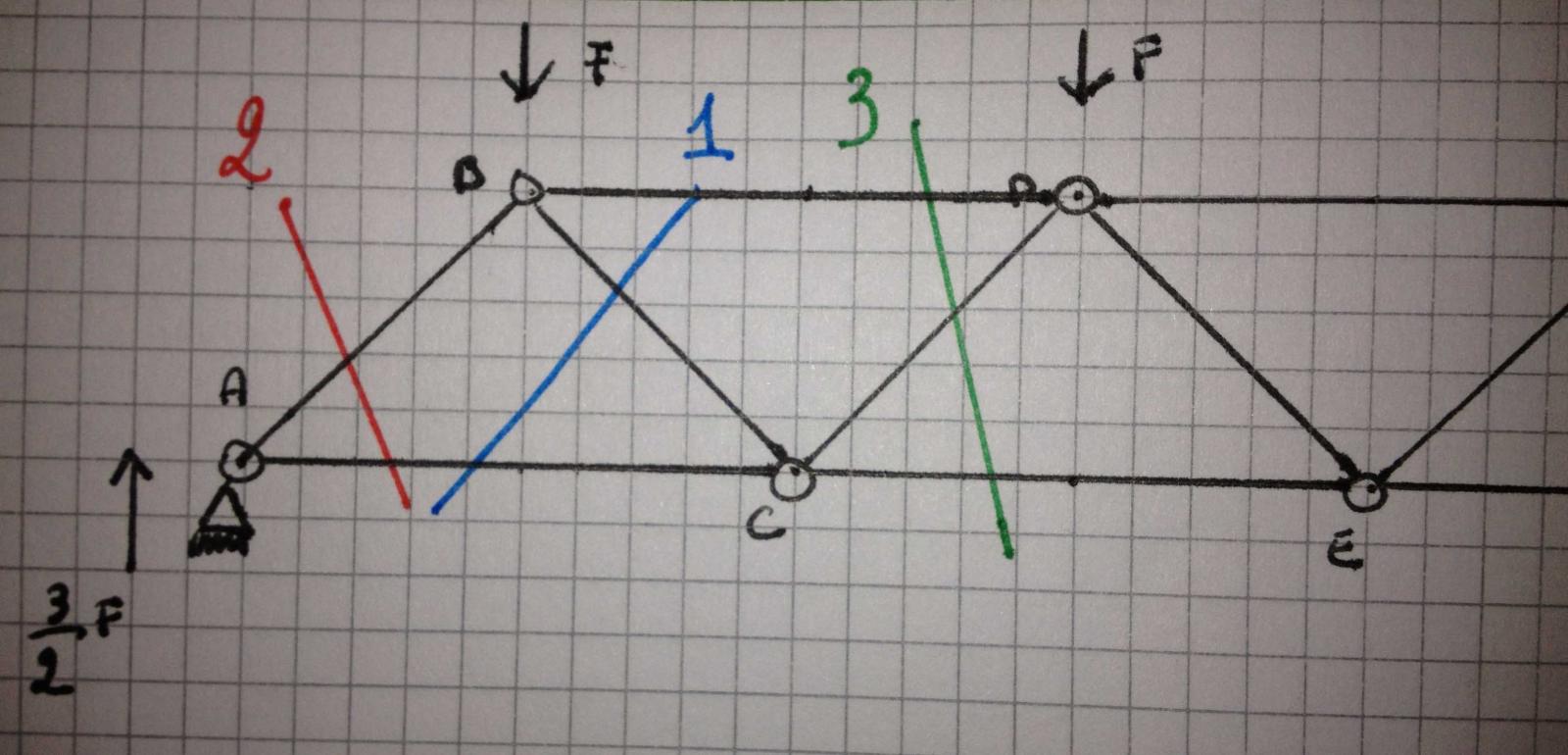
Posso fare l'equilibrio nelle singole sezioni ricavate:

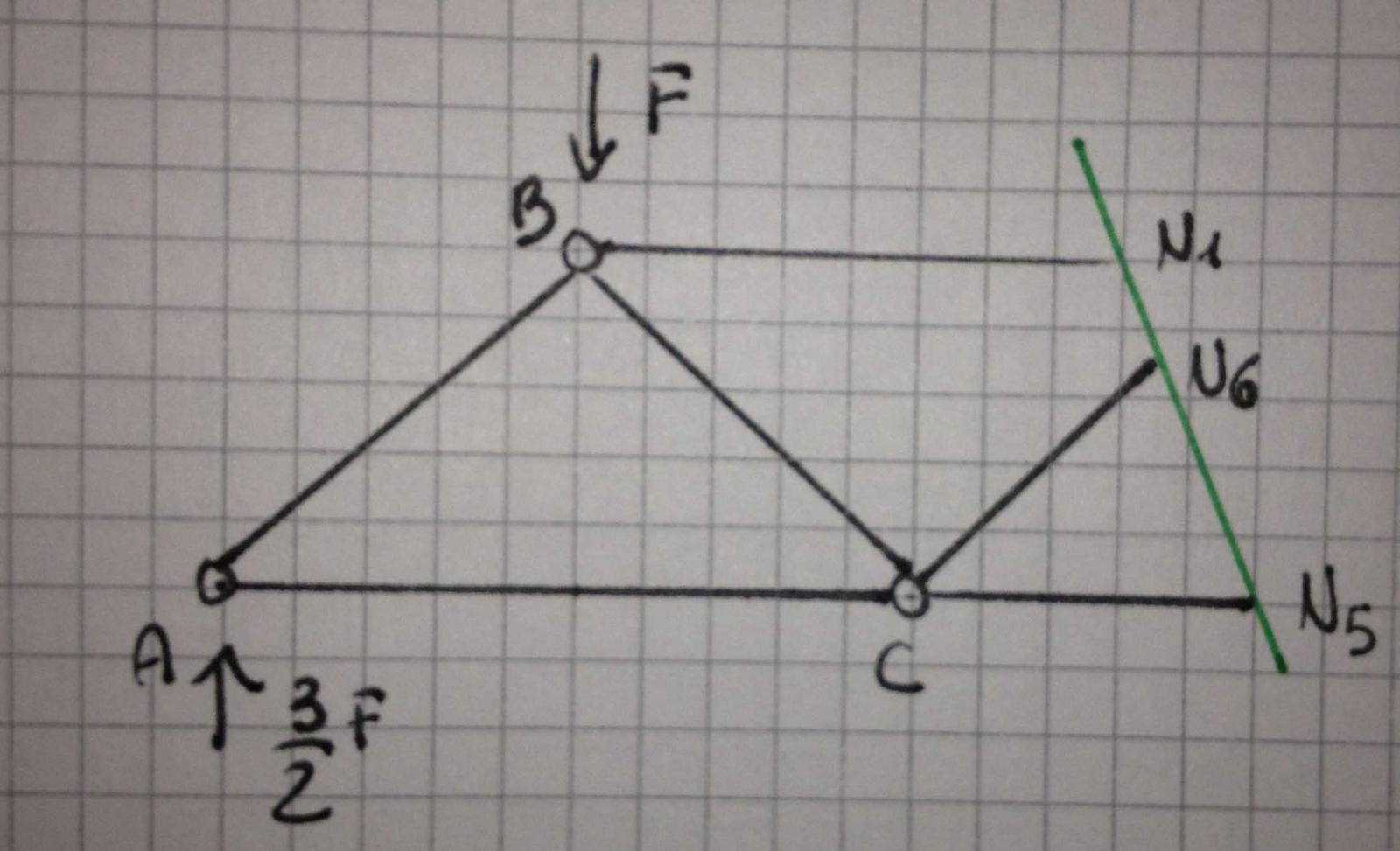
SEZIONE 1

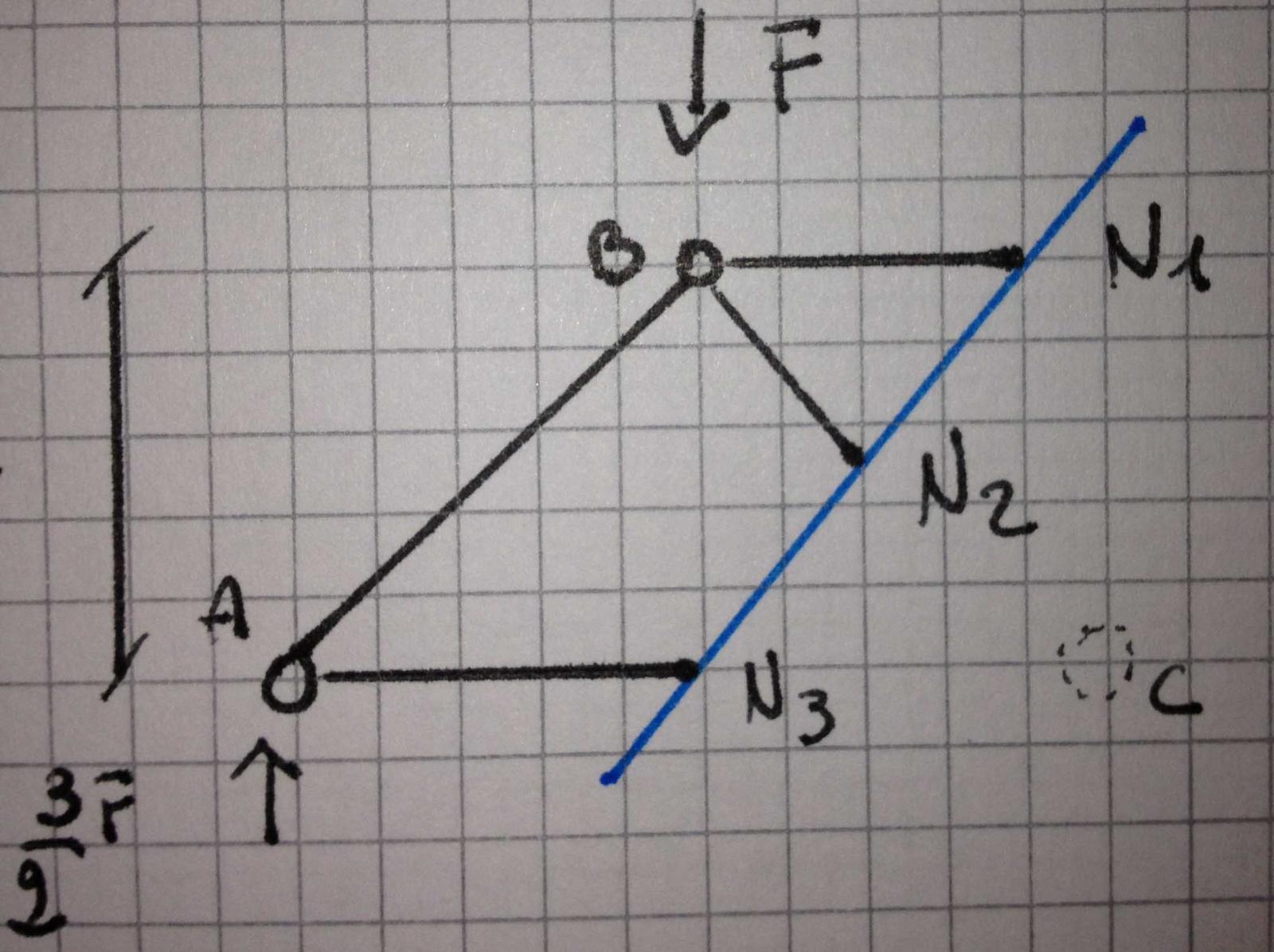
Ipotizziamo la positività. Se il risultato è negativo, cambiamo il verso. 

Facendo l'equilibrio intorno a C , possiamo ricavare N1: -3/2(l) + F(l) - N1(l) ====> N1=-2F

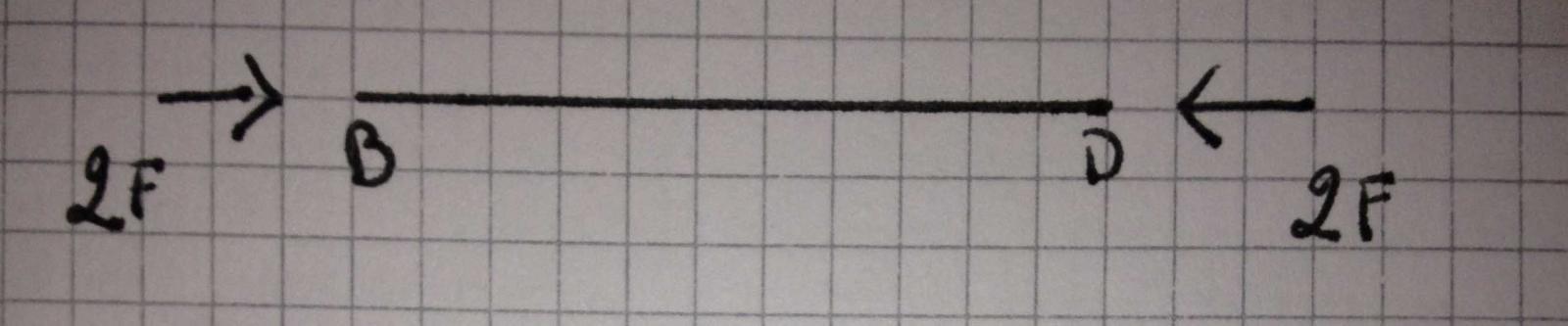
L'asta appare compressa

Facendo l'equilibrio intorno a B possiamo ricavare N3: -3/2 F(l) + N3 (l) ====> N3=3/2F

La trave appare tesa.

Per quanto riguarda N2, facciamo la scomposizione delle forse, come diagonale di un quadrato:

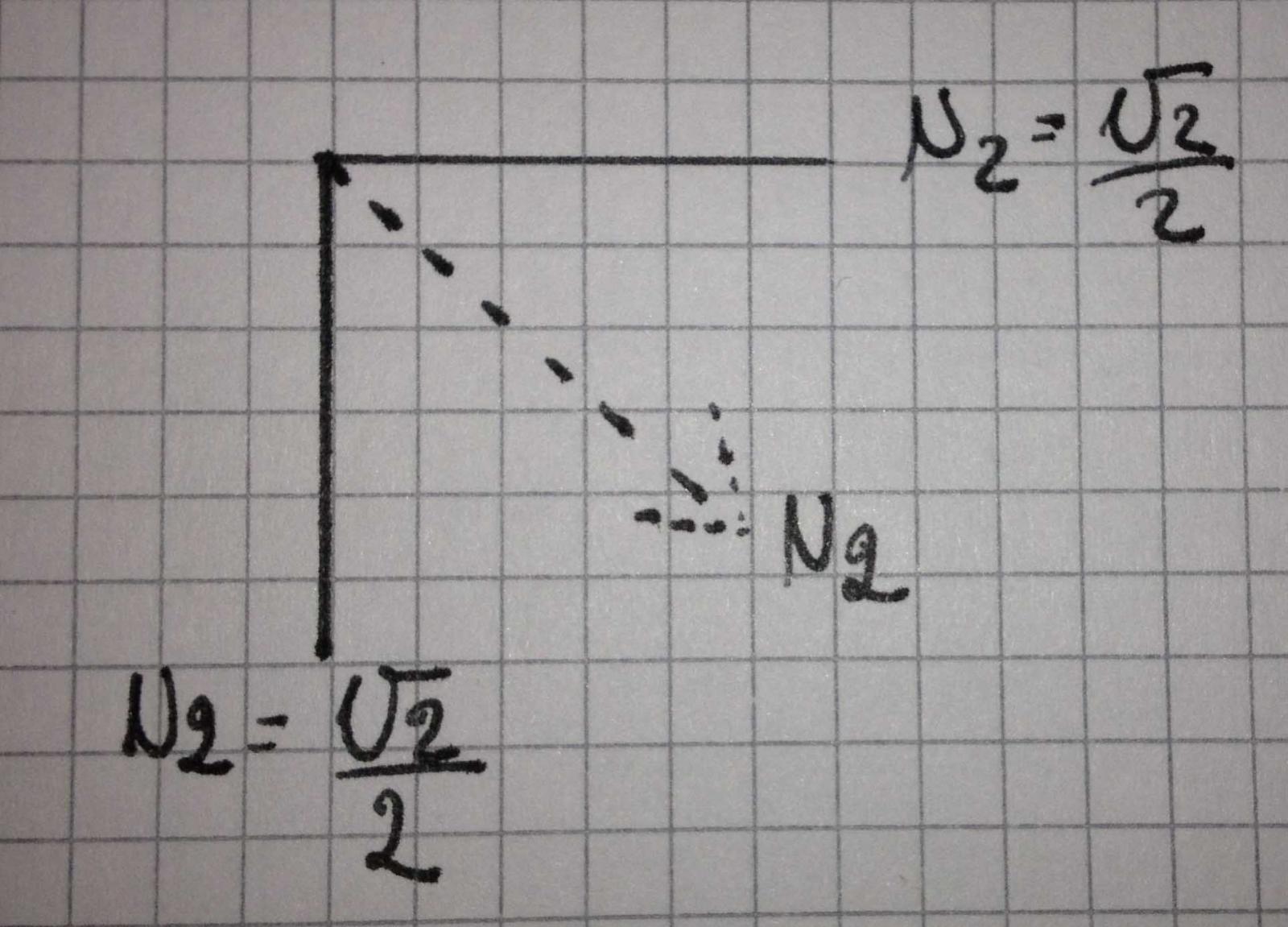
quindi N2= -F/2 x radice di 2 x radice di 2= F radice di 2/ 2

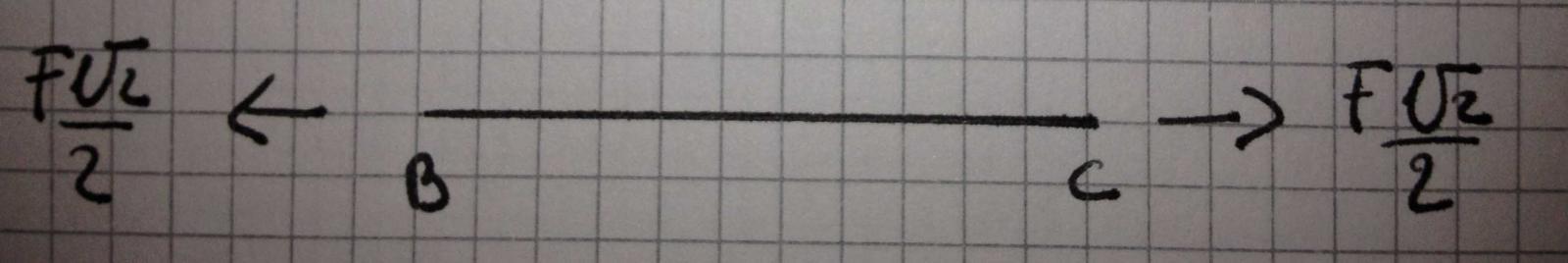
la trave appare tesa

SEZIONE 2 

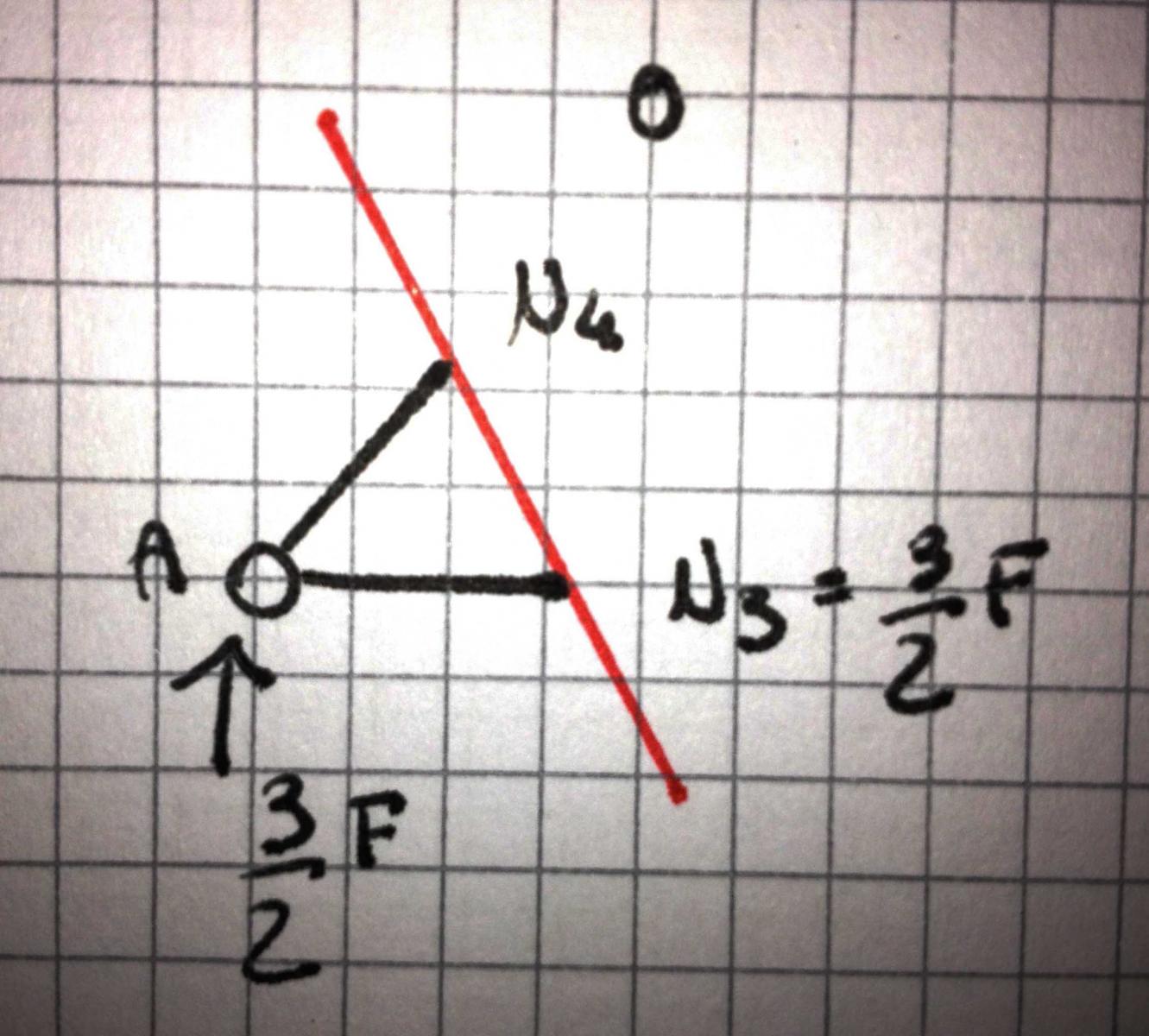
N3 è nota dalla sezione precedente, quindi sarà sufficiente conoscere N4. N4 presenta le stesse condizioni della N2 precedente, quindi la scomponiamo come diagonale di un quadrato, e otteniamo: 

N4= -3/2 F radice di 2

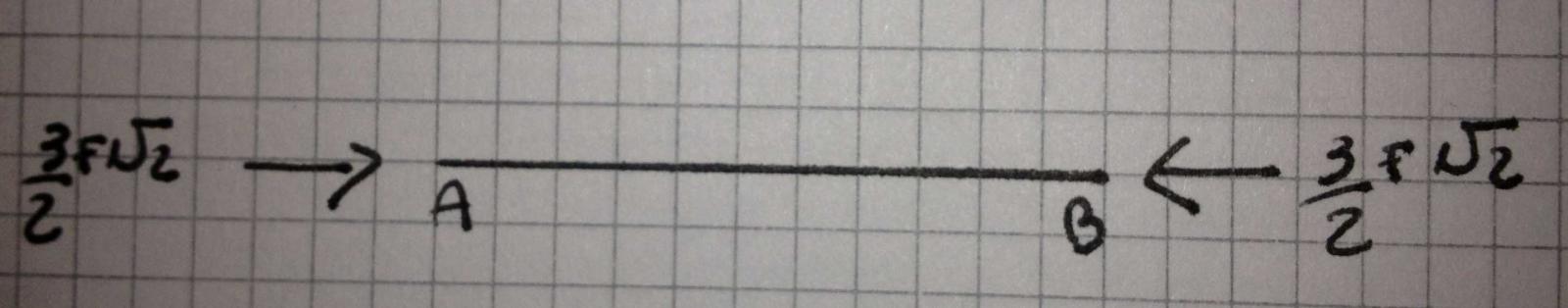
L'asta appare compressa

SEZIONE 3

Conosciamo N1, possiamo fare la rotazione in D per ottenere N5: N5 (l) + F "2l)- 3/2 F (3l) = 0 ====>N5=5/2F

l'asta appare tesa

Facendo l'equilibrio verticale,e utilizzando il metodo della scomposizione, ricaviamo N6=Fradice di 2 / 2 

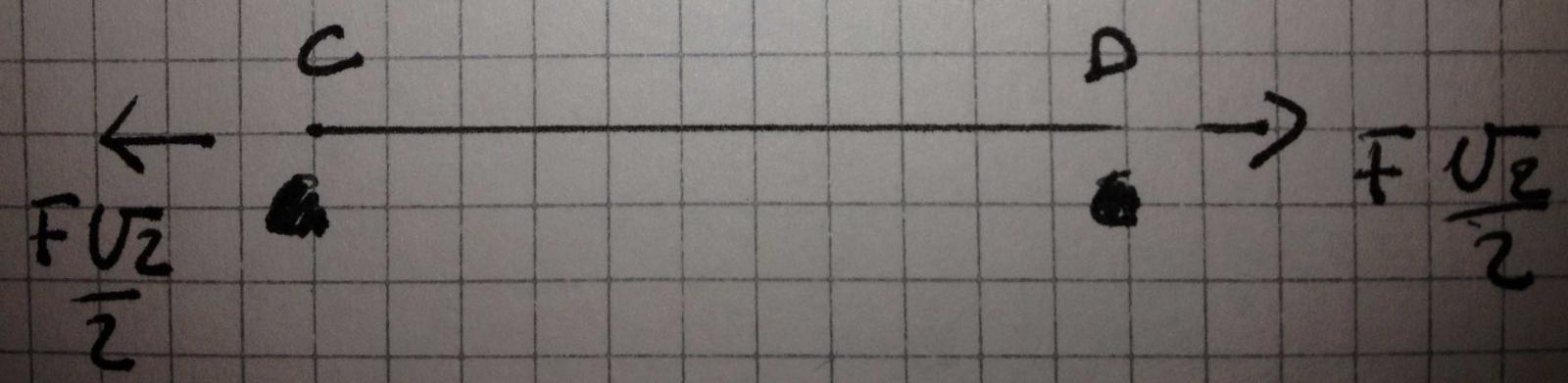
L'asta appare tesa

Saluti

Mimmo Piergiacomi