Esercitazione_TRAVE RETICOLARE verifica con Sap2000

Con Travatura reticolare si intende un sistema di aste appartenenti allo stesso piano e vincolate  reciprocamente ai nodi attraverso cerniere interne (incastri) caricate esternamente in modo da costituire un elemento resistente e indeformabile.

Le aste sono soggette a solo sforzo normale se questo è di compressione allora l'asta si dice PUNTONE se invece esso è di trazione si dice TIRANTE. La travatura reticolareè formata da due elementi continui chiamati correnti, e da un'anima scomposta in elementi lineari. Gli elementi verticali vengono denominati montanti, quelli inclinati vengono chiamati diagonali. La travatura reticolare è tratta dalla necessità di utilizzare strutture leggere e che permettessero di raggiungere grandi luci.

Un primo aspetto da analizzare è il Problema dell' ISOSTATICITA'.

dove i gradi di libertà devono essere uguali ai gradi di vincolo. In un piano ogni corpo ha 3 gradi di libertà (traslazione verticale, orizzontale e rotazione). Il n0stro sistema è composto da 33 aste (33x3=9 gradi di libertà).

Per calcolare il grado di vincoli uso la seguente formula: 2(n-1) dove n= numero di aste che convergono in un nodo.

Nei nodi A e T confluiscono 2 aste: 2(2-1)=2 (ma il punto A è doppiamente vincolato dalla presenza della cerniera che ha 2 vincoli) quindi A= 4 vincoli invece il punto T ha un vincolo carrello quindi 1 vincolo sommando i due valori T = 3 vincoli

Nei nodi B,M,U confluiscono 3 aste: 2(3-1)=4vincoli ognuno

Nei nodi C,D,E,G,H,I,N,O,P,Q,R,S confluiscono 4 aste: 2(4-1)=6 vincoli ognuno

Nel nodo L confluiscono 5 aste: 2(5-1)=8vincoli ognuno

sommiamo:

4+3+(4x3)+(6x12)+8 = 99 vincoli

99 vincoli = 99 gradi di libertà

la travatura  è ISOSTATICA

I metodi principali di calcolo di una travatura reticolare isostatica sono principalmente due:

1. Metodo di equilibrio ai nodi (se la travatura è in equilibrio ogni nodo deve essere in equilibrio. Esso considere le forze concentrate sui nodi e sa che le aste sono soggette solo a sforzo normale; viene studiato un modello che utilizza la regola del palallelogramma per la scomposizione delle forze. Per ogni nodo le incognite risolvibili sono 2. Le equazioni di equilibrio alla traslazione verticale e orizzontale)Perchè il nodo sia in equilibrio l risultante delle forze (verticale o orizzontale)deve essere uguale a zero.
2. Metodo della sezione di Ritter la sezione di Ritter è una sezione che divide (con un taglio virtuale) in due la struttura tagliando tre aste non convergenti nello stesso nodo. Una volta effettuato il taglio, si mettono in evidenza gli sforzi normali agenti sulle sezioni delle aste tagliate.

METODO DELLE SEZIONI DI RITTER 

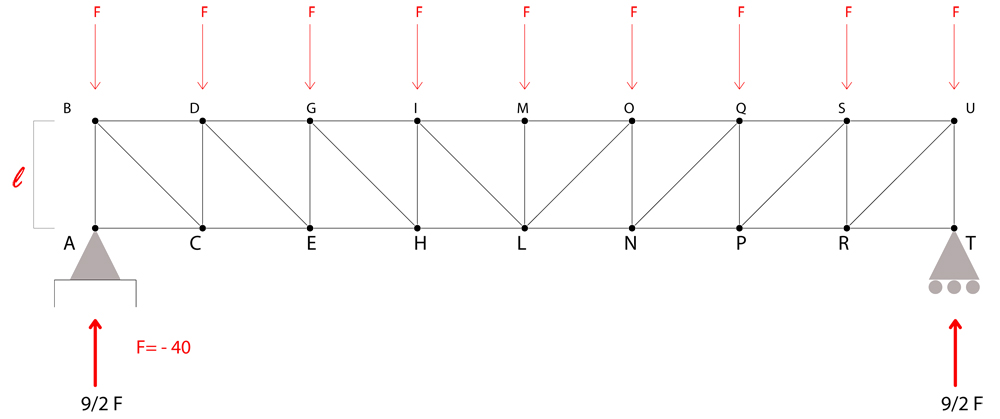
I VINCOLI si ripartiscono il carico 9/2F a destra e a sinistra.

La struttura è isostatica e simmetrica e caricata simmetricamente, per questo dividiamo la struttura in due parti. Nel sistema isostatico si possono trovare le reazioni vincolari del carrello e cerniera esterni che vengono considerati come dati dal problema.

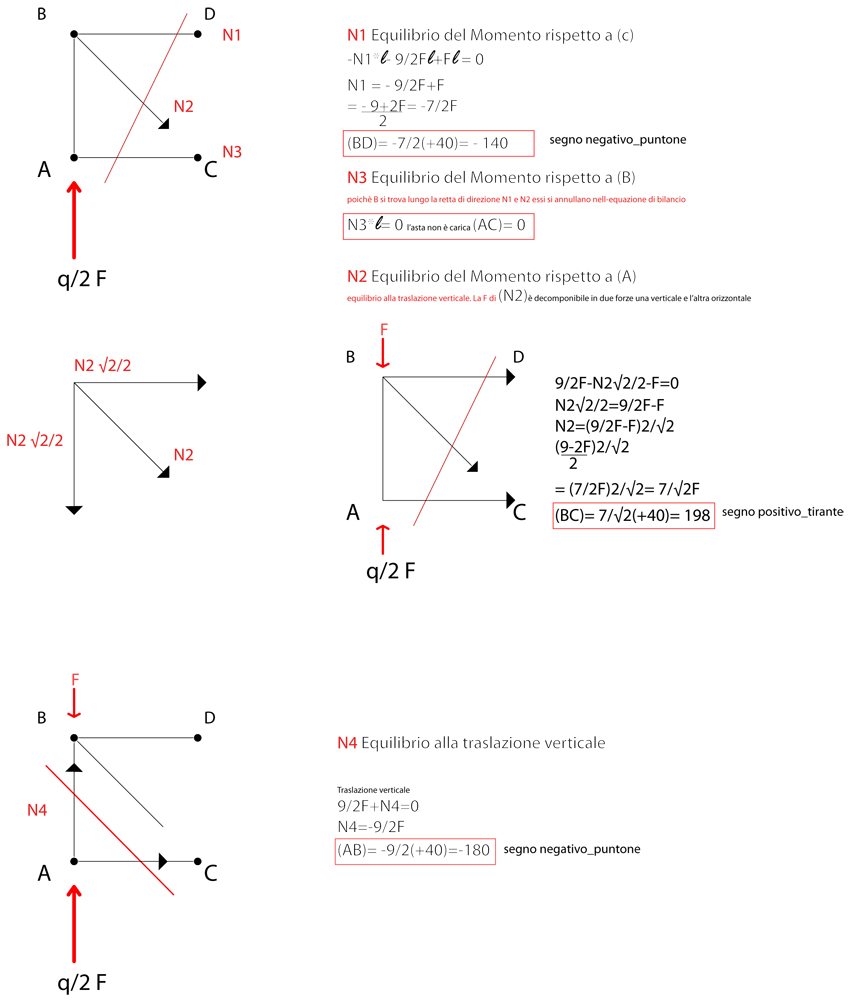
Effettuo il primo taglio virtuale di 3 aste, disegno le 3 forze N1, N2 e N3  uscenti dalla sezione (posso scegliere arbitrariamente il verso delle forze perchè verranno poi confermate o no in seguito dal risultato delle equazioni di equilibrio).

In seguito determino i valori di N1, N2 e N3 (le incognite sono tre e tre sono le equazioni di bilancio). La regola che viene suggerita è quella di scrivere tre equazioni di equilibrio a rotazione rispetto a un nodo in cui convegono 2 delle 3 aste che non sono l'asta incognita che si sta cercando.

Iniziamo con il primo taglio:

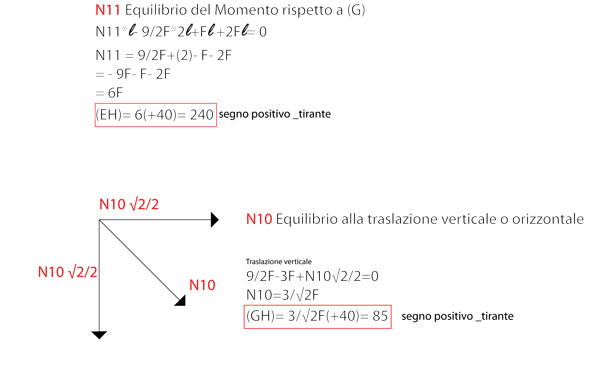
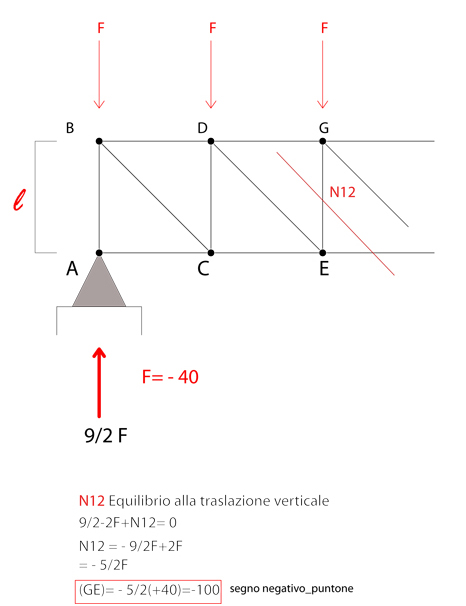
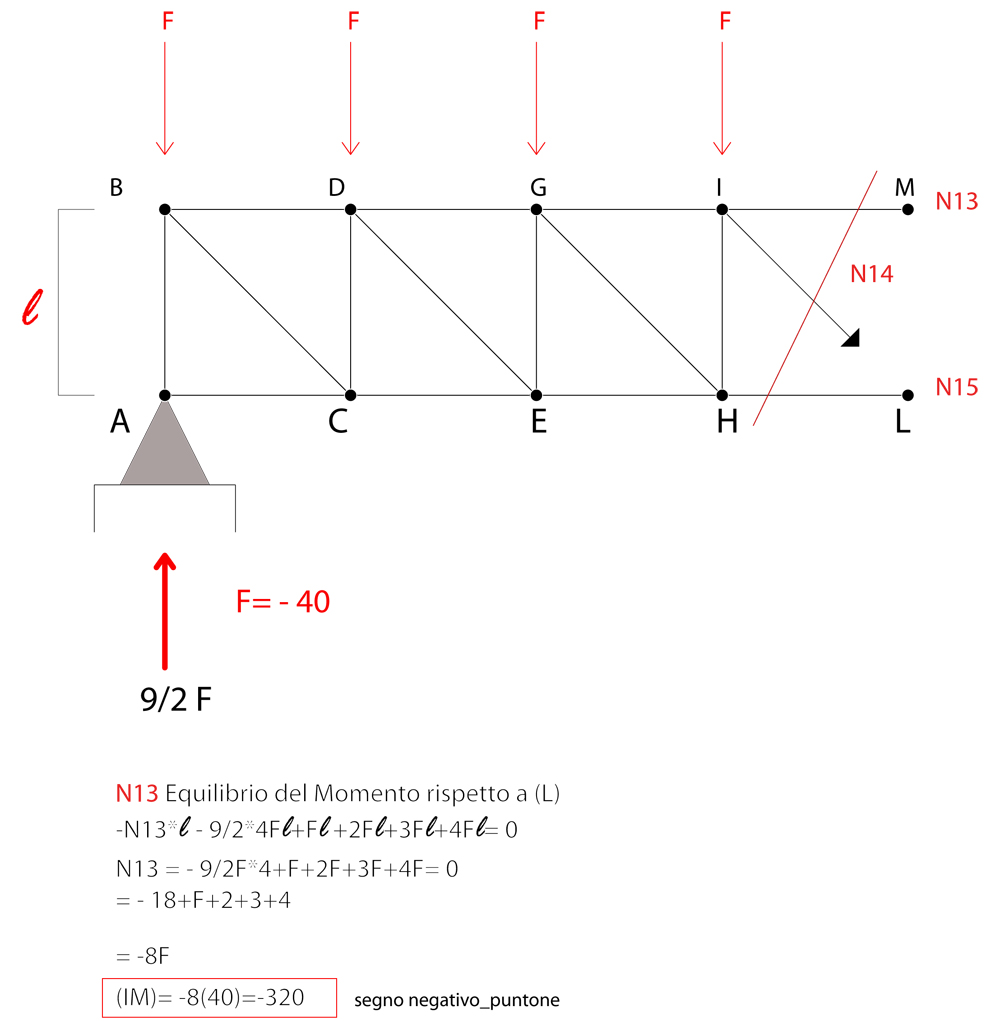
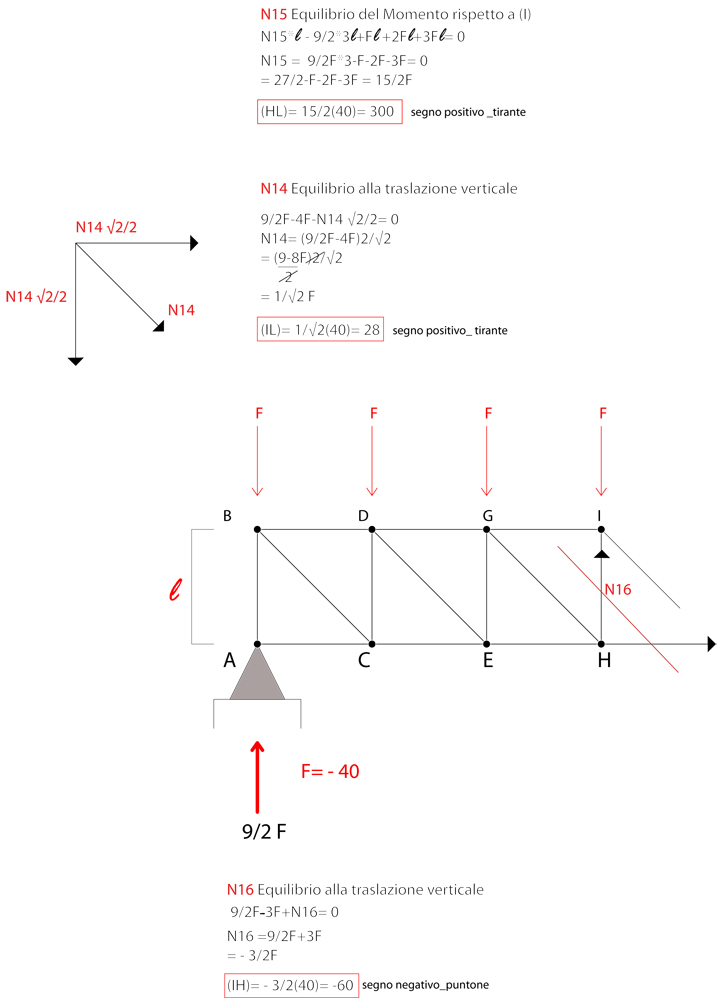
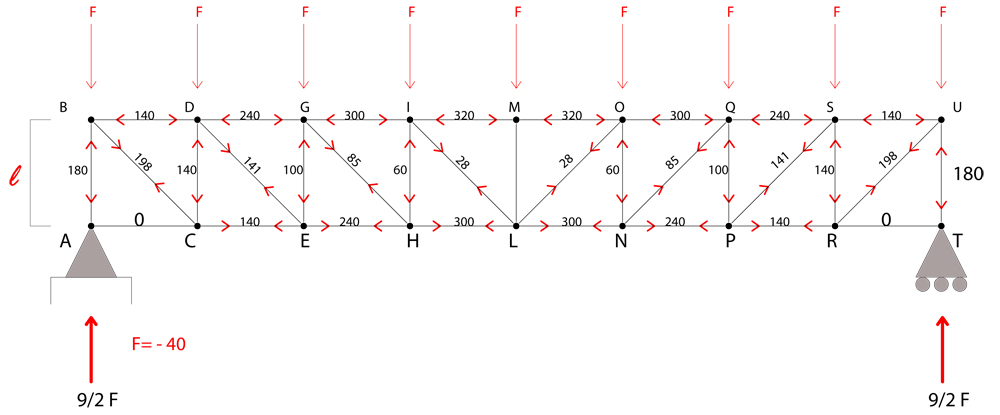
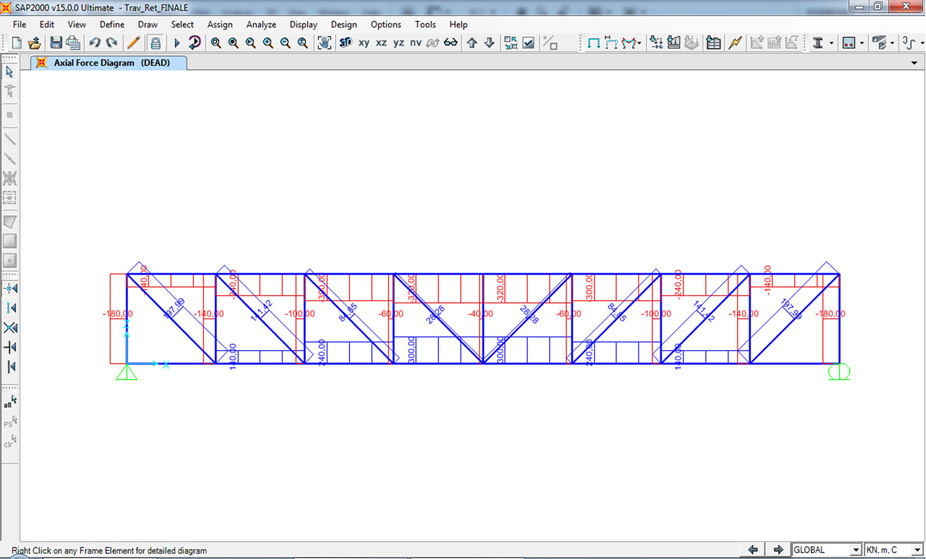
VERIFICA SU SAP2000 TRAVE RETICOLAE 2D