Esercitazione: Trave iperstatica e calcolo con Sap2000

Risoluzione di una struttura iperstatica

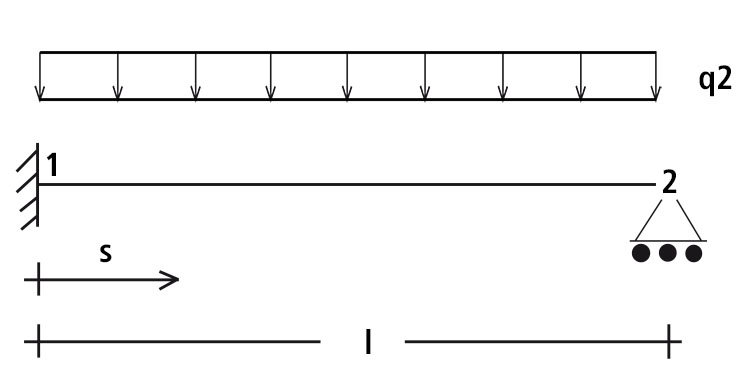
Per risolvere questo tipo di trave andiamo ad analizzare i tre gruppi di equazioni della trave di Eulero Bernoulli (equazioni di equilibrio, legami costitutivi, equazioni di compatibilità)

Potremmo escludere da questi tre gruppi tutte le equazioni contenenti i termini  u, N e ε (poichè non abbiamo uno spostamento orizzontale) ed accorpare le rimanenti equazioni in un unico sistema

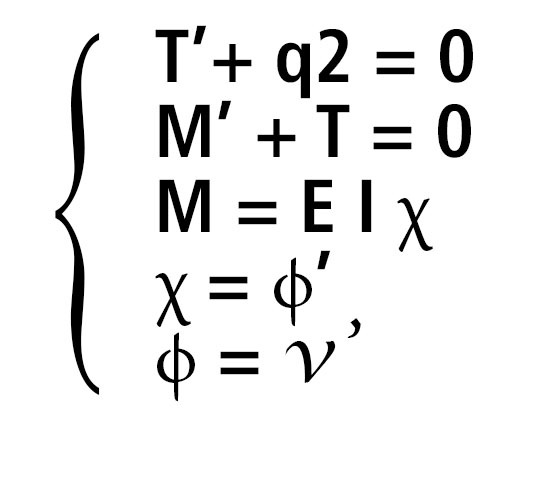
Ora vado ad unire T'+q2=0 con M'+T=0 :           -[(d²M)/(dS²)]+q2=0
Posso unire anche anche χ = ϕ’ con ϕ = v’ :       χ= d²v/dS²

Grazie all’ultima componente del sistema (M = E I χ) potrò formulare un unica equazione che contiene tutte le altre:    EI*(d⁴v/dS⁴)=q2

Ora vado a derivare l’equazione differenziale imponendo il termine q2 come costante

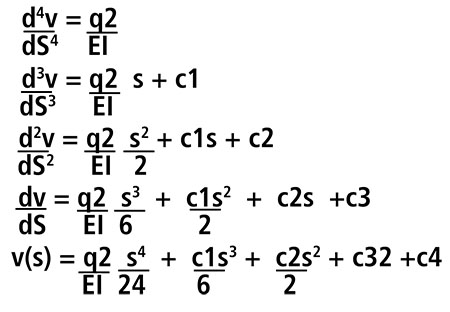
Ora posso ottenere il valore dello spostamento (v) andando a ricavare le incognite c.
Le incognite possono essere ricavate ponendo il valore di s=l e s=0

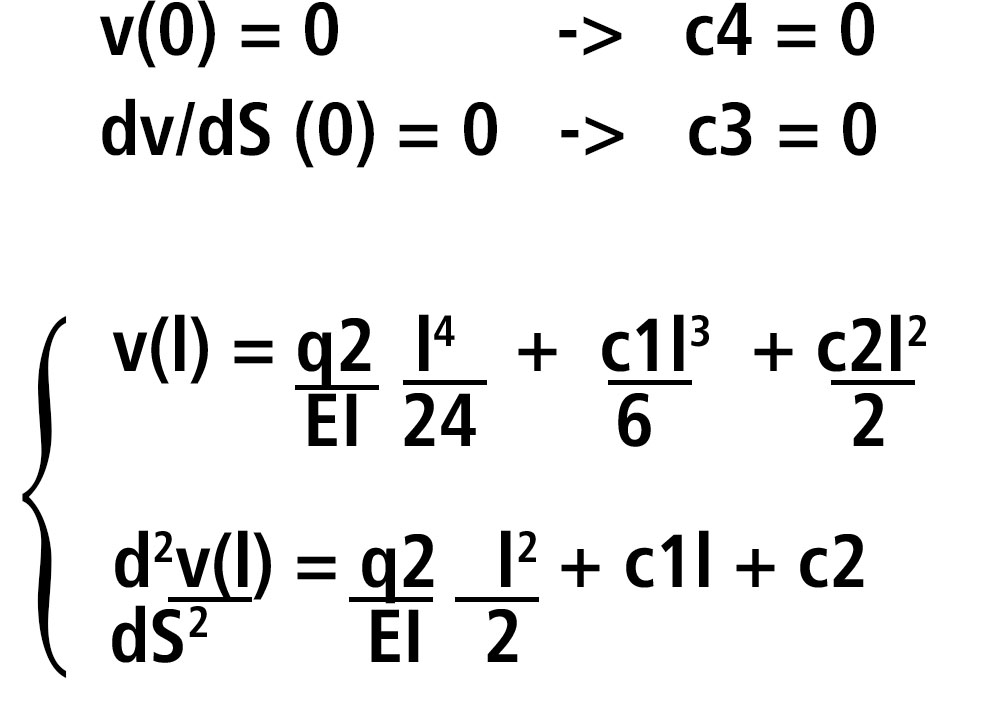
Ottenuto il sistema vado a ricavare le uniche incognite rimaste (c1;c2)

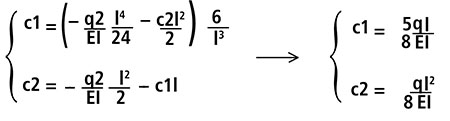
Conoscendo ora tutte le incognite (c1;c2;c3;c4) posso sostituirle in v(s) per trovare il valore di s

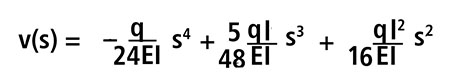
Il primo risultato che troviamo è s=0 per gli altri due risultati applichiamo la formula risolutiva delle equazioni di secondo grado ottenendo i due risultati:

s = +0,57 l     s = +1,513 l

Di questi due valori prenderemo solo il primo (s= +0,57 l) poichè la trave ha una lunghezza:  0 < l < 1

A questo punto inserisco il vaore di s in v(s) =>   v(0,57) ed ottengo la distanza s in cui il momento è massimo:

s = 0,57

Risoluzione della struttura in SAP 2000

Per prima cosa disegno la struttura, definisco l'unità di misura (KN,m,C), ed assegno i carichi

Poi assegno un carico distribuito di 10 N/m su tutta la struttura

Associo alla trave un profilo rettangolare in calcestruzzo (Assign->Frame->Frame Sections)

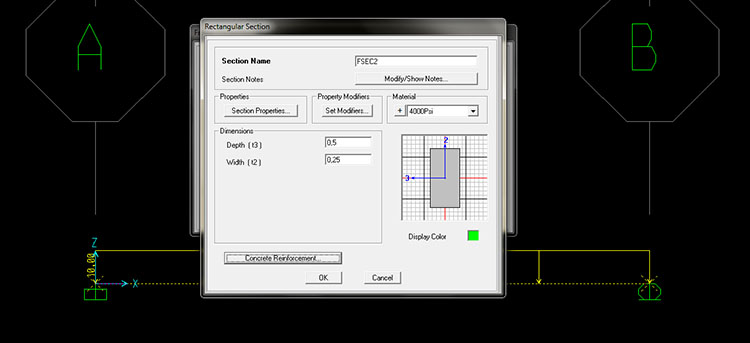
Questo profilo (probabilmente eccessivo) determina una deformata in cui l'inflessione è così impercettibile che il software non la mostra

Ripeto il passaggio precedente associando alla struttura un profilo tubolare in acciaio

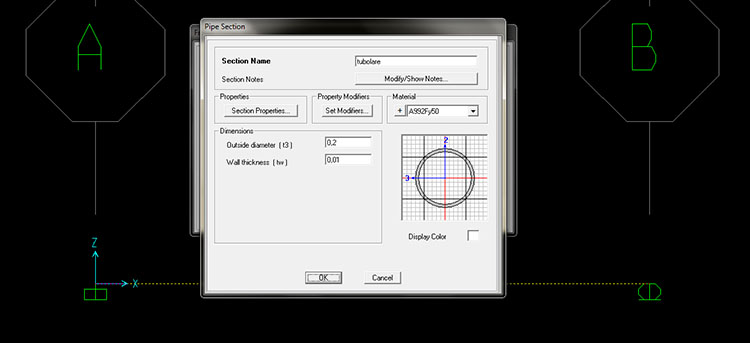
Avvio il calcolo della struttura (Run Analysis)

Dal diagramma del monmento posso verificare che il momento massimo (0,67) si trova esattamente ad una distanza pari a 0,57