Esercitazione 2 - Risoluzione di un sistema iperstatico mediante il metodo dell'integrazione della linea elastica

RISOLUZIONE DI UN SISTEMA IPERSTATICO MEDIANTE L'INTEGRAZIONE DELLA LINEA ELASTICA

Partendo da questo schema statico su cui è applicato un carico distribuito (q) è richiesto di trovare l'abbassamento massimo che da questo carico è provocato. Dato che il sistema è iperstatico per risolverlo non può essere usato il classico metodo dell'equilibrio dei corpi liberi per via delle troppe incognite (4) a fronte delle sole 3 equazioni necessarie a determinare l'equilibrio. Il metodo che l'esercizio stesso suggerisce di applicare è quello dell'integrazione della linea elastica.

Questo metodo collega i 3 gruppi di equazioni che descrivono il comportamento meccanico del modello strutturale in esame, che presenta le caratteristiche della trave di Eulero-Bernoulli (trave sintetizzata come asse rispetto al quale ogni sezione è perpendicolare, carichi spostamenti e deformazioni nel piano). Esse sono:

L'incognita principale è lo spostamento verticale, e non ci sono carichi orizzontali agenti sulla struttura (di conseguenza nemmeno reazioni vincolari orizzontali ne sollecitazioni assiali), quindi possiamo escludere 3 di queste 8 equazioni, ottenendo questo sistema:

Procedendo per sostituzione e integrando si risale ad un equazione utile a ricavare lo spostamento verticale v in funzione di s.

È necessario precisare che la trave ha sezioni uguali in ogni punto ed è composta di un materiale uniforme, di conseguenza E ed I sono costanti lungo tutto l'intervallo di s, come lo è q. Questo semplifica notevolmente il procedimento di integrazione.

Integrando si generano delle costanti, che non sono però incognite: esse assumono un valore a seconda delle condizioni di vincolo al bordo, il punto di partenza per la risoluzione dell'esercizio.

Sono necessarie 4 equazioni con risultato noto per trovare le 4 costanti d'integrazione, si esaminano quindi i vincoli dati dall'esercizio per capire cosa è noto:

• Per s = 0 abbiamo lo spostamento verticale e la rotazione nulle (v=0 e φ=0). Da questo deriva che c₃ e c₄ hanno valore nullo (per sostituzione nell'equazione di v(s)).

• Per s = L abbiamo che lo spostamento verticale è sempre nullo (v=0), è consentita la rotazione che però è ignota, quindi si considera l'equazione del momento. È noto che in cerniera esso è nullo, e di conseguenza la stessa curvatura ha valore nullo (Χ=0):

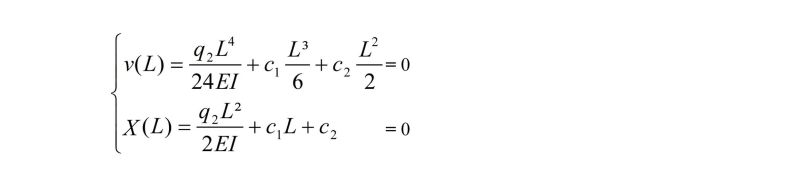
Svolgendo i calcoli si determinano i valori di c₁ e c₂:

L'equazione di v è espressa in funzione di s, che varia da 0 ad L. Per conoscere il valore di s che corrisponde all'abbassamento massimo (che corrisponde al punto di minimo, con tangenza orizzontale quindi) è sufficiente risolvere v'(s)= 0.

L'equazione è di terzo grado e presenta 3 soluzioni. Una è maggiore di L (quindi da scartare), la seconda è 0 e la terza è 0,578L, l'obiettivo del calcolo.

A questo punto si torna all'equazione di v(s), che non presenta più incognite. Sostituendo i valori di c₁, c₂ ed s si ottiene il valore dell'abbassamento in funzione di L, E, I e q. Questi dipendono dalle condizioni di progetto e di carico (L e q), dalla geometria della sezione scelta (I, il momento d'inerzia) e dal materiale utilizzato (E, il modulo elastico).

È possibile determinare qualitativamente i diagrammi di taglio e momento flettente.

Il taglio presenta un andamento lineare, con valore negativo all'incastro e positivo sul carrello, e si azzera a 5/8L.

Il momento flettente presenta quindi un andamento parabolico con un valore massimo positivo nell'incastro, è nullo in corrispondenza del carrello e il vertice della parabola in questione è situato in corrispondenza del punto in cui il taglio è nullo. 

VERIFICA SU SAP DEI DATI OTTENUTI CON APPLICAZIONE DI 2 DIVERSE SEZIONI

Per rappresentare lo schema statico su SAP viene aperto un nuovo file di tipo GRID, con unità di misura convenzionali (kN, m, °C). Impostati i parametri di spaziatura di modo che L sia pari ad 1, impostata correttamente la vista, si (piano XZ) disegna un punto P di coordinate (0.578, 0, 0), ovvero il punto ricavato mediante il calcolo manuale in cui l'abbassamento è massimo, e si disegna una trave usando 2 segmenti, che condividono un estremo proprio in quel punto. Il programma non li leggerà come 2 elementi distinti, ma come un unico elemento strutturale.

Successivamente vengono impostati i vincoli (incastro e carrello) e il carico associato a un corretto load pattern con peso proprio degli elementi strutturali nullo (carico distribuito, di 100kN/m).

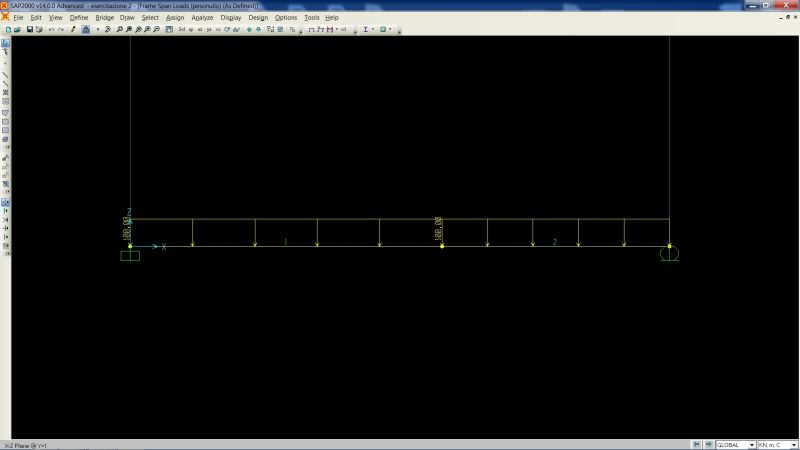
Manca unicamente di impostare un tipo di sezione alla trave.

Qui si aprono 2 possibilità: l'esercizio deve essere svolto con sezione rettangolare in CLS non armato (0.20x0.40m) e con sezione rettangolare cava in acciaio (0.10x0.15m, con spessore di 0.004m).

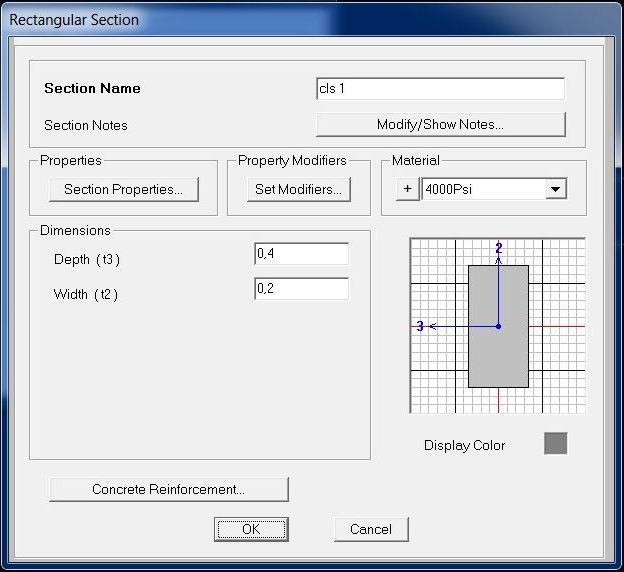
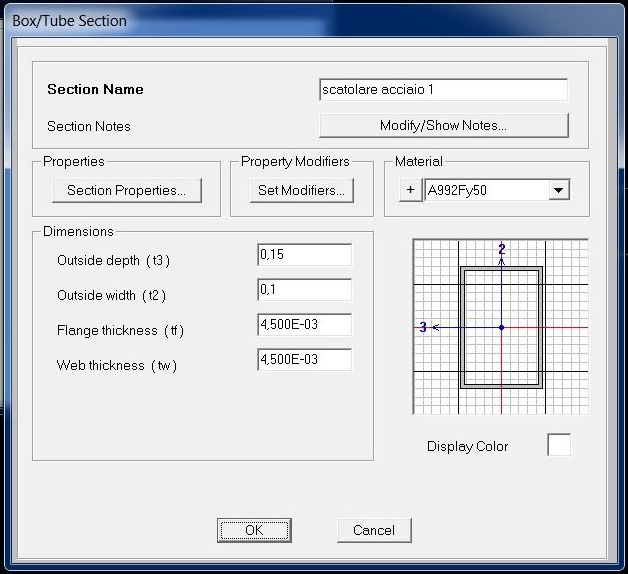
Dopo aver assegnato a entrambi i segmenti le sezioni precedentemente impostate va svolta l'analisi per i carichi assegnati, escludendo l'analisi modale.

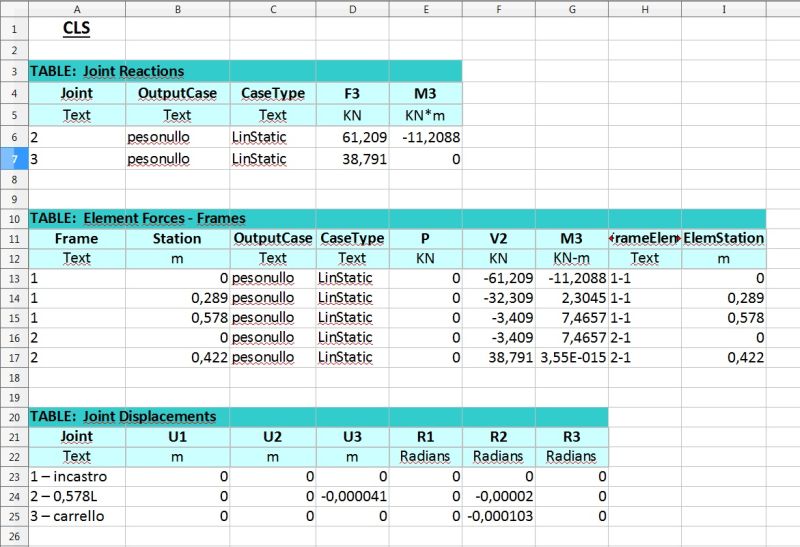
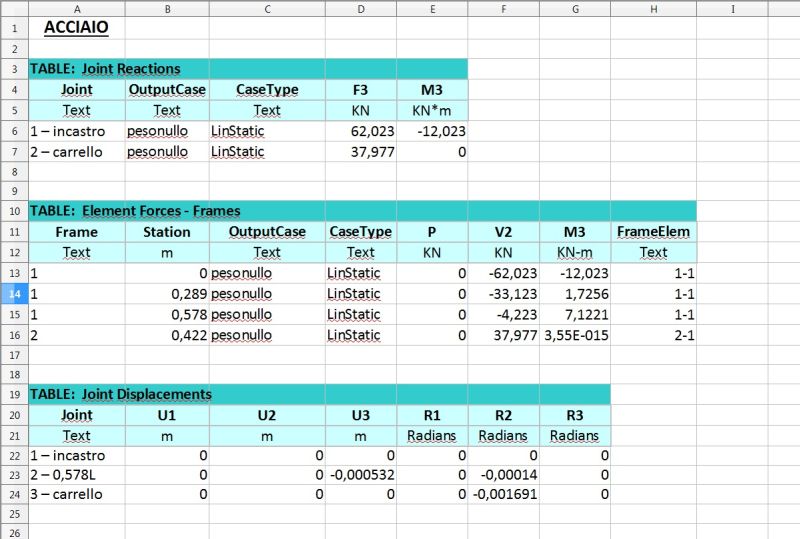
Il programma mostra direttamente la deformata, che conferma la correttezza (con un certo grado di approssimazione) del calcolo manuale utilizzato per il posizionamento del punto a 0,578l.

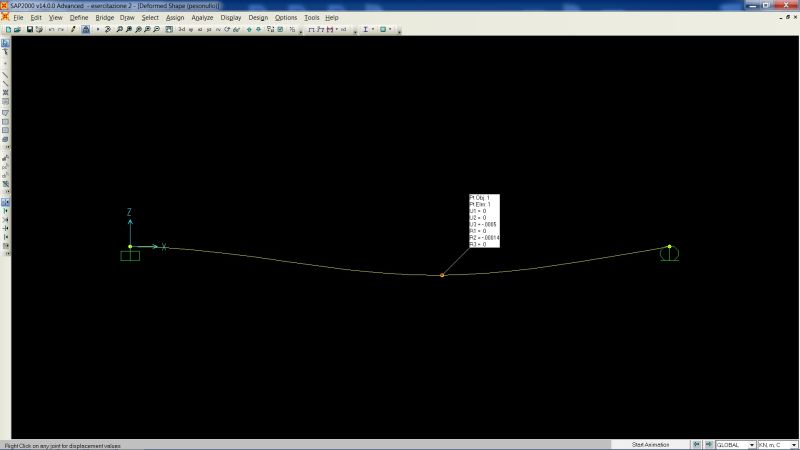
Posizionando il cursore su tale punto, che graficamente sembra essere proprio sul minimo della deformata, viene rivelato l'abbassamento (che varia in base alla Section Property associata alla trave) e le rotazioni della sezione. Essa, nella direzione di nostro interesse, è prossima allo zero: infatti nel punto di minimo è per definizione nulla, essendo la tangente in quel punto orizzontale.

Verificati e confrontati i grafici di T ed M rappresentati al livello qualitativo alla fine dell'esercizio manuale con quelli che il programma fornisce si visualizzano ed esportano su excel le tabelle per arrivare ai valori precisi di reazioni vincolari e sollecitazioni. Eseguendo l'analisi per ognuna delle 2 sezioni precedentemente impostati si arriva ad ulteriori dati, gli abbassamenti e le rotazioni.

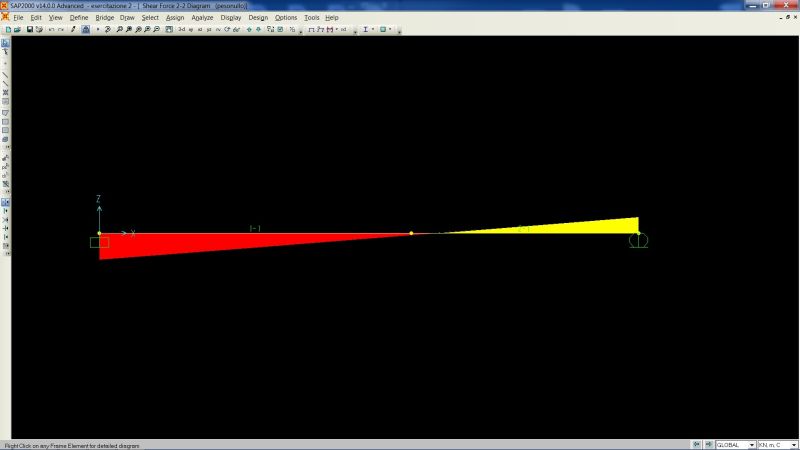
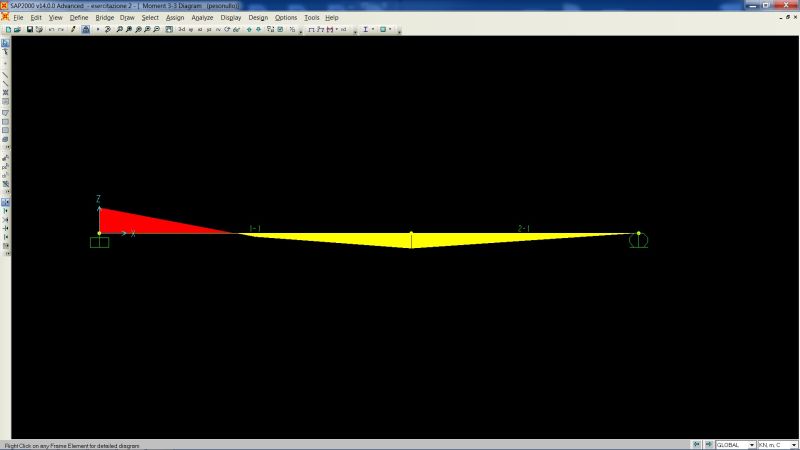
TABELLE CON RISULTATI