Esercitazione_3_analisi dei carichi e dimensionamento di una trave (risoluzione tramite foglio Excel)

 

Esercitazione_3

analisi dei carichi e dimensionamento di una trave (risoluzione tramite foglio Excel)

 

1_

inquadramento edificio

L’edificio presenta un solo solaio posizionato fuori terra ed in testata una torre alta tre piani. La tecnologia scelta per la realizzazione dell’edificio sarà in funzione del dimensionamento delle travi e dei materiali usati.

 

 

 

 

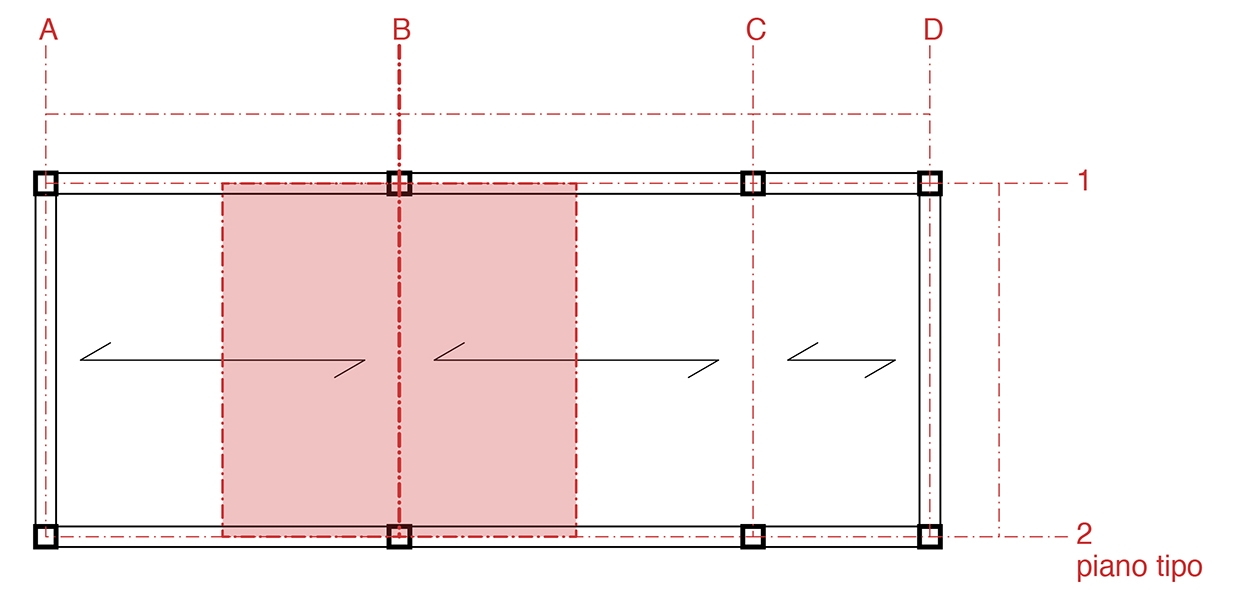
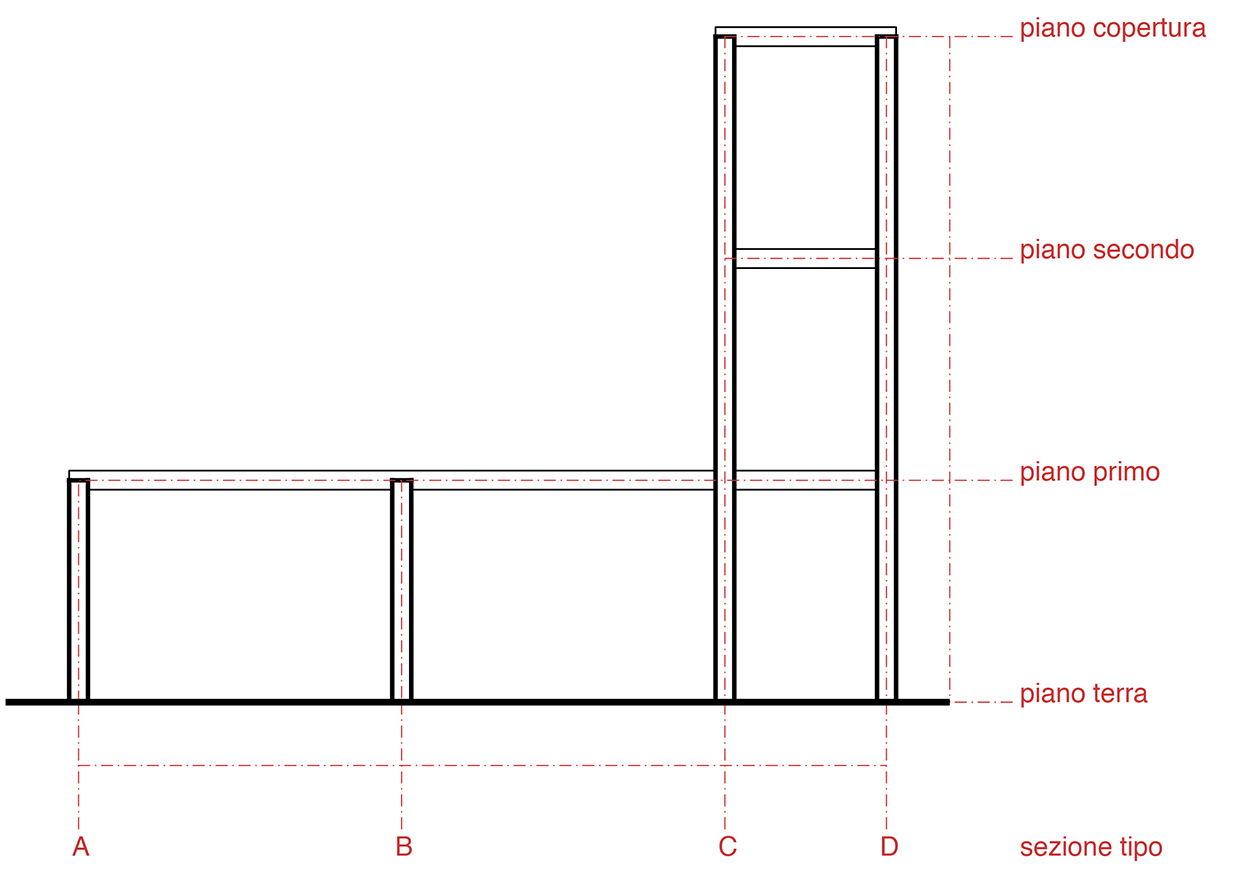
destinazione d’uso

L’edificio ospita uffici ed uno spazio comune nella parte più alta della torre. Internamente l’edificio si presenta munito di pannelli scorrevoli che definiscono una maggiore flessibilità per lo spazio interno. L’incidenza degli impianti nei controsoffitti e il valore di carico accidentale saranno dunque importanti nel calcolo.

 

2.1_

stratrigrafia solaio_1

 

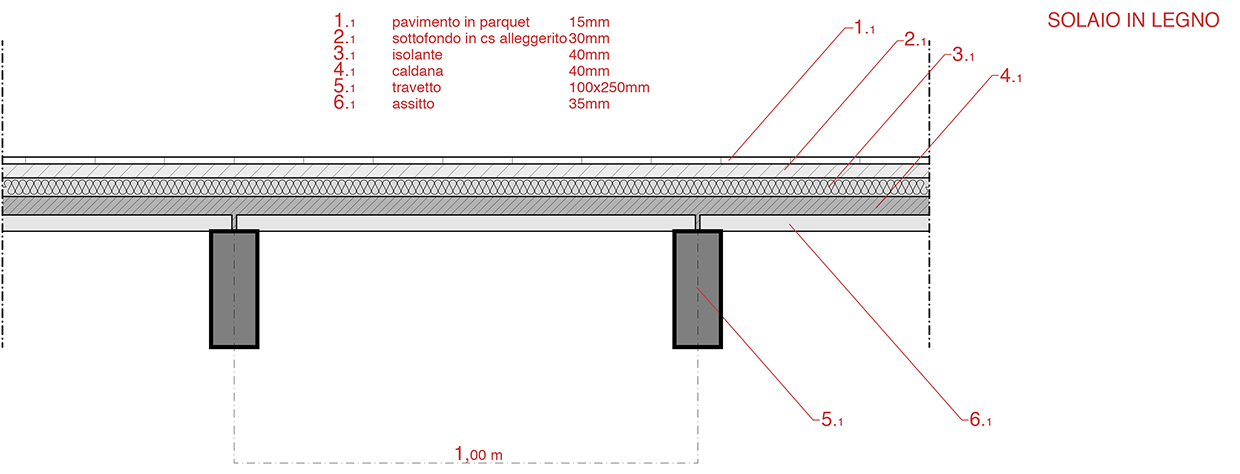
analisi dei carichi

.solaio in legno

_carichi strutturali_qs

_tavolato 0,020 kN/m²

_travicelli 600kg/m³ 0,050 kN/m²

_caldana 0,100 kN/m²

-----------------------------------------------------------------------------------------------------

_totale c.s 0,170 kN/m²

 

_carichi permanenti_qp

_incidenza tramezzi 0,500 kN/m²

_incidenza impianti 1,000 kN/m²

_pavimento in parquet 750kg/m³ 0,220 kN/m²

_massetto in cs allegerito 1,000 kN/m²

_muro di tamponamento in tufo 1,800 kN/m²

-----------------------------------------------------------------------------------------------------

_totale c.p 4,520 kN/m²

 

_carichi accidentali_qa

_ambiente uffici 3,000 kN/m²

-----------------------------------------------------------------------------------------------------

_totale c.a 3,000 kN/m²

-----------------------------------------------------------------------------------------------------

_totale 7,690 kN/m²

 

_carico proprio della trave_qs*

Successivamente alla progettazione della sezione della trave, verrà aggiunto il peso proprio della stessa. Il calcolo verrà fatto moltiplicando la sezione per la lunghezza della trave e per il peso specifico del materiale di progetto. Il dimensionamento verrà concluso con la verifica della resistenza della trave calcolato con il nuovo momento flettente, vedendo di conseguenza la sua risposta.

 

3.1_

Per il progetto della trave si è proseguito con l’analisi del carico totale ricavato dall’analisi dei carichi. Questo valore è stato successivamente moltiplicato per l’interasse dell’area che interessava, ricavandosi di conseguenza il carico uniformemente distribuito sulla trave B-B’ presa in esame.

 

q= (qs + qp + qa) *i ⇒ q= (0,170 + 4,520 + 3,000)kN /m² *5,100m

⇒ q= 39,22kN /m

 

Successivamente al calcolo del carico distribuito che insiste sulla trave viene calcolato il momento flettente massimo MMAx che insiste sulla sezione della stessa. Il momento viene calcolato tenendo in considerazione le condizioni di vincolo della trave, e presentando essa una situazione semplicemente appoggiata ad una cerniera a sinistra ed un carrello a destra si può procedere al calcolo del momento massimo flettente mediante la formula:

 

MMAX= (q*L²)/8 ⇒ MMAX= (39,22*5,10²)/8

⇒ MMAX= 127,51kN*m

 

Definito il momento massimo di progetto, si calcola la resistenza di progetto fd, definita dalla motiplicazione della resistenza caratteristica del materiale di progetto (in questo caso legno) per il coefficiente di degrado nel tempo kmod (che descrive la durata del carico e la classe di servizio) e diviso per il coefficiente di sicurezza γm (= 1,45 per l’acciaio), come si può vedere nella formula:

 

fd=  kmod * fmk/γm ⇒ fd= (0,60*24)/1,45

⇒ fd= 9,93N/mm²

 

Ricavate le resistenze di progetto del materiale si può procedere per il dimensionamento dell’altezza della trave usando la formula flessionale di Navier:

 

fd= σMAX ⇒ σMAX = 9,93N/mm²

σMAX= MMAX/Wx ⇒ Wx= Jxx / (h/2)

⇒ Wx= MMAX/σMAX

⇒ Wx= (127,51*10⁶) / 9,93 

⇒ Wx= 12’840’886,20mm³

⇒ Wx= 12’840,89cm³

Wx= MMAX/σMAX

Wx= Jxx / (h/2) ⇒ Jxx = (b * h³)/12

MMAX= (q*L²)/8

⇒ Jxx / (h/2) = ((q*L²)/8)/σMAX

⇒ ((b * h³)/12) / (h/2) = ((q*L²)/8)/σMAX

⇒ h²= (6 * q*L²)/(8 * b * σMAX)

⇒ h= √(6 * q*L²)/(8 * b * σMAX)

Per procedere per il dimensionamento dell’altezza della trave, si ipotizza una base di una di base di b (= 25 cm), attraverso la formula flessionale di Navier viene ricavata l’altezza h:

 

⇒ h= √(6 * 39,22 * (5,1*1000)²)/(8 * (25*10) * 9,93)

⇒ h= 555,10mm

⇒ h= 57,00cm

 

4.1_

Per verificare che il progetto della trave sia corretto in toto si procede con il calcolo del peso proprio della trave, il quale peso verrà aggiunto alla fase dell’analisi dei carichi, con i quali verrà ricavato un nuovo momento massimo che verificherà la resistenza della trave.

 

_carichi strutturali_qs

_tavolato 0,020 kN/m²

_travicelli 600kg/m³ 0,050 kN/m²

_caldana 0,100 kN/m²

_trave in latifoglie 1,140 kN/m²

-----------------------------------------------------------------------------------------------------

_totale c.s 1,131 kN/m²

 

_carichi permanenti_qp

_incidenza tramezzi 0,500 kN/m²

_incidenza impianti 1,000 kN/m²

_pavimento in parquet 750kg/m³ 0,220 kN/m²

_massetto in cs allegerito 1,000 kN/m²

_muro di tamponamento in tufo 1,800 kN/m²

-----------------------------------------------------------------------------------------------------

_totale c.p 4,520 kN/m²

 

_carichi accidentali_qa

_ambiente uffici 3,000 kN/m²

-----------------------------------------------------------------------------------------------------

_totale c.a 3,000 kN/m²

-----------------------------------------------------------------------------------------------------

_totale 8,651 kN/m²

 

q= (qs + qp + qa) *i ⇒ q= (1,131 + 4,520 + 3,000)kN /m² *5,100m

⇒ q= 44,12kN /m

MMAX= (q*L²)/8 ⇒ MMAX= (44,12*5,10²)/8

⇒ MMAX= 143,45kN*m

σMAX= MMAX/Wx ⇒ Wx= Jxx / (h/2)

⇒ Wx= MMAX/σMAX

⇒ Wx= (143,45*10⁶) / 9,93 

⇒ Wx= 14’446’122,12mm³

⇒ Wx= 14’446,12cm³

Wx= MMAX/σMAX

Wx= Jxx / (h/2) ⇒ Jxx = (b * h³)/12

MMAX= (q*L²)/8

Per procedere per il dimensionamento dell’altezza della trave, si ipotizza una base di b (= 25 cm), attraverso la formula flessionale di Navier viene ricavata l’altezza h:

 

⇒ h= √(6 * 44,12 * (5,1*1000)²)/(8 * (25*10) * 9,93)

⇒ h= 588,80mm

⇒ h= 60,00cm

Si adotta di conseguenza una trave di base b (= 25 cm) e altezza h (= 60 cm) avente modulo di resistenza Wx (= 15’000,00cm³) pari o superiore a quello ricavato dalla formula flessionale di Navier.

 

5.1_

dati di progetto e tabella

 

 

interasse (m)	qs (KN/m2)	qp (KN/m2)	qa (KN/m2)	q (KN/m)	luce (m)	M (KN*m)	fm,k (N/mm2)
5,1	0,170	4,520	3,00	39,219	5,1	127,51077375	24
5,1	1,131	4,520	3,00	44,120	5,1	143,445475125	24

 

 

 

kmod	sigam (N/mm2)	b (cm)	h (cm)
0,6	9,93	25	55,51
0,6	9,93	25	58,88

2.2_

stratrigrafia solaio_2

 

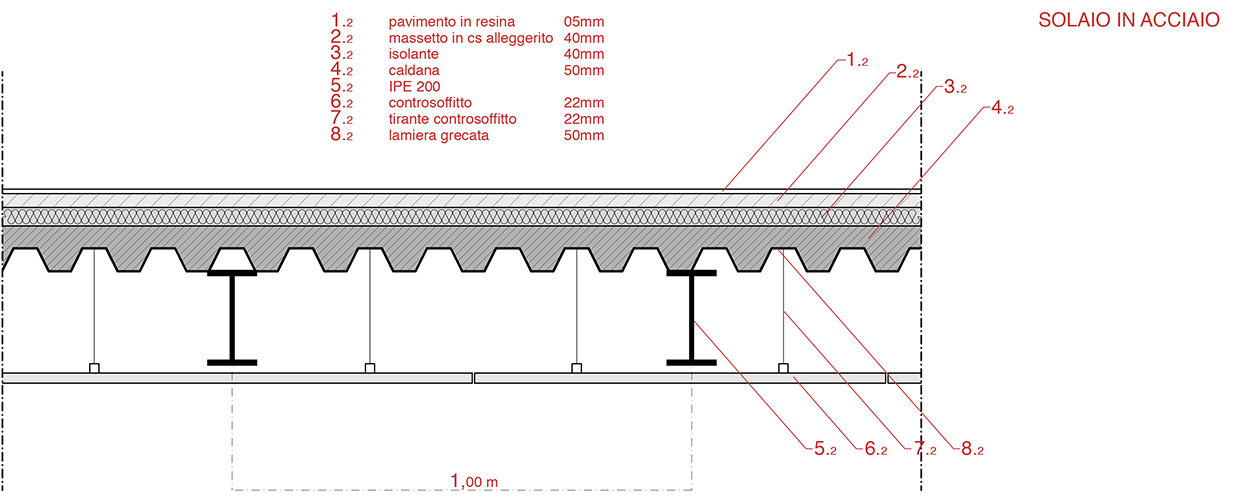
analisi dei carichi

.solaio in acciaio

_carichi strutturali_qs

_solaio in lamiera grecata di acciaio 0,240 kN/m²

_travetti in IPE 200 1,141 kN/m²

-----------------------------------------------------------------------------------------------------

_totale c.s 1,381 kN/m²

 

_carichi permanenti_qp

_incidenza tramezzi 0,500 kN/m²

_incidenza impianti 1,000 kN/m²

_pavimento in resina 0,003 kN/m²

_massetto in cs allegerito 1,000 kN/m²

_controsoffito in cartongesso 8kg/m² 0,010 kN/m²

_muro di tamponamento in tufo 1,800 kN/m²

-----------------------------------------------------------------------------------------------------

_totale c.p 4,313 kN/m²

 

_carichi accidentali_qa

_ambiente uffici 3,000 kN/m²

-----------------------------------------------------------------------------------------------------

_totale c.a 3,000 kN/m²

-----------------------------------------------------------------------------------------------------

_totale 8,694 kN/m²

 

_carico proprio della trave_qs*

Successivamente alla progettazione della sezione della trave, verra aggiunto il peso proprio della trave. Il calcolo verrà fatto moltiplicando la sezione per la lunghezza della trave e per il peso specifico del materiale di progetto. Il dimensionamento verrà concluso con la verifica della resistenza della trave calcolato con il nuovo momento flettente, vedendo di conseguenza la sua risposta.

 

3.2_

Per il progetto della trave si è proseguito con l’analisi del carico totale ricavato dall’analisi dei carichi. Questo valore è stato successivamente moltiplicato per l’interasse dell’area che interessava, ricavandosi di conseguenza il carico uniformemente distribuito sulla trave B-B’ presa in esame.

 

q= (qs + qp + qa) *i ⇒ q= (1,381 + 4,313 + 3,000)kN /m² *5,100m

⇒ q= 44,34kN /m

 

Successivamente al calcolo del carico distribuito che insiste sulla trave viene calcolato il momento flettente massimo MMAx che insiste sulla sezione della stessa. Il momento viene calcolato tenendo in considerazione le condizioni di vincolo della trave, e presentando essa una situazione semplicemente appoggiata ad una cerniera a sinistra ed un carrello a destra si può procedere al calcolo del momento massimo flettente mediante la formula:

 

MMAX= (q*L²)/8 ⇒ MMAX= (44,34*5,10²)/8

⇒ MMAX= 144,15kN*m

 

Definito il momento massimo di progetto, si calcola la resistenza di progetto fd, definita dalla motiplicazione della resistenza caratteristica del materiale di progetto (in questo caso acciaio) diviso per il coefficiente di sicurezza γs (= 1,15 per l’acciaio), come si può vedere nella formula:

 

fd= fyk/γs ⇒ fd= 235/1,15

⇒ fd= 204,35N/mm²

 

Ricavate le resistenze di progetto del materiale si può procedere per il dimensionamento dell’altezza della trave usando la formula flessionale di Navier:

 

fd= σMAX ⇒ σMAX = 204,35N/mm²

σMAX= MMAX/Wx ⇒ Wx= Jxx / (h/2)

⇒ Wx= MMAX/σMAX

⇒ Wx= (144,15*10⁶) / 204,35 

⇒ Wx= 705’407,39mm³

⇒ Wx= 705,47cm³

 

Si adotta di conseguenza un IPE 330 avente modulo di resistenza Wx (= 713,00cm³) pari o superiore a quello ricavato dalla formula flessionale di Navier.

 

4.2_

Per verificare che il progetto della trave sia corretto in toto si procede con il calcolo del peso proprio della trave, il quale peso verrà aggiunto alla fase dell’analisi dei carichi, con i quali verrà ricavato un nuovo momento massimo che verificherà la resistenza della trave.

 

_carichi strutturali_qs

_solaio in lamiera grecata di acciaio 0,240 kN/m²

_travetti in IPE 200 1,141 kN/m²

_trave in IPE 330 2,506 kN/m²

-----------------------------------------------------------------------------------------------------

_totale c.s 3,587 kN/m²

 

_carichi permanenti_qp

_incidenza tramezzi 0,500 kN/m²

_incidenza impianti 1,000 kN/m²

_pavimento in resina 0,003 kN/m²

_massetto in cs allegerito 1,000 kN/m²

_controsoffito in cartongesso 8kg/m² 0,010 kN/m²

_muro di tamponamento in tufo 1,800 kN/m²

-----------------------------------------------------------------------------------------------------

_totale c.p 4,313 kN/m²

 

_carichi accidentali_qa

_ambiente uffici 3,000 kN/m²

-----------------------------------------------------------------------------------------------------

_totale c.a 3,000 kN/m²

-----------------------------------------------------------------------------------------------------

_totale 10,900 kN/m²

 

q eff = (qs + qp + qa)*i ⇒ q eff = (3,587 + 4,313 + 3,000)kN /m² *5,100m

⇒ q eff = 55,59kN /m

MMAXeff= (q*L²)/8 ⇒ MMAXeff= (55,59*5,10²)/8

⇒ MMAXeff= 180,74kN*m

 

σMAX= MMAX/Wx ⇒ Wx= (180,74*10⁶) / 204,35 

⇒ Wx= 884’462,93mm³

⇒ Wx= 884,46cm³

 

Si adotta di conseguenza un IPE 360 avente modulo di resistenza Wx (= 904,00cm³) pari o superiore a quello ricavato dalla formula flessionale di Navier.

 

5.2_

dati di progetto e tabella

 

 

interasse (m)	qs (KN/m2)	qp (KN/m2)	qa (KN/m2)	q (KN/m)	luce (m)	M (KN*m)
5,1	1,381	4,313	3,00	44,34	5,10	144,15847425
5,1	3,587	4,313	3,00	55,59	5,10	180,7369875

 

 

 

fy,k (N/mm2)	sigam (N/mm2)	Wx (cm3)
235	204,35	705,46
235	204,35	884,46

2.3_

stratrigrafia solaio_3

 

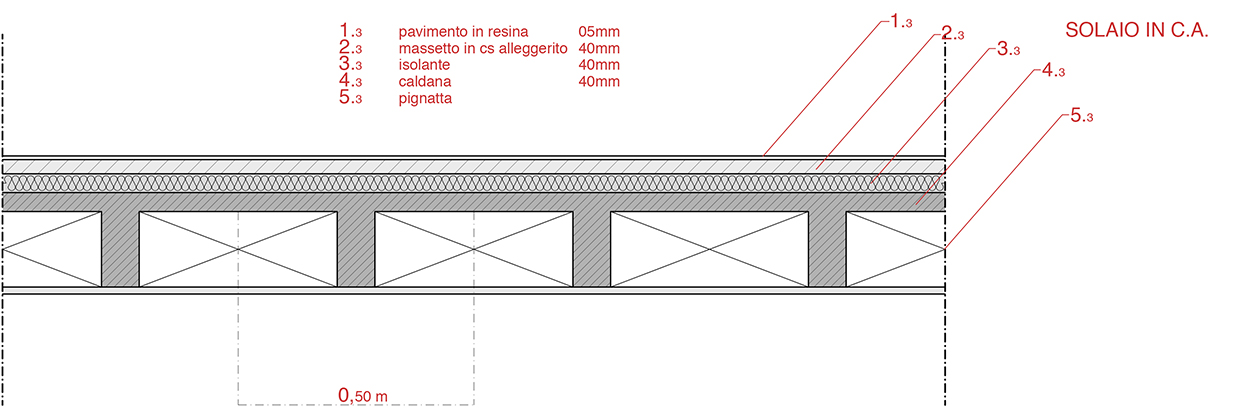
analisi dei carichi

.solaio in c.a.

_carichi strutturali_qs

_solaio in latero-cemento 2,700 kN/m²

----------------------------------------------------------------------------------------------------

_totale c.s 2,700 kN/m²

 

_carichi permanenti_qp

_incidenza tramezzi 0,500 kN/m²

_incidenza impianti 1,000 kN/m²

_pavimento in resina 0,003 kN/m²

_massetto in cs allegerito 1,000 kN/m²

_muro di tamponamento in tufo 1,800 kN/m²

-----------------------------------------------------------------------------------------------------

_totale c.p 4,303 kN/m²

 

_carichi accidentali_qa

_ambiente uffici 3,000 kN/m²

-----------------------------------------------------------------------------------------------------

_totale c.a 3,000 kN/m²

-----------------------------------------------------------------------------------------------------

_totale 10,003 kN/m²

 

_carico proprio della trave_qs*

Successivamente alla progettazione della sezione della trave, verra aggiunto il peso proprio della trave. Il calcolo verrà fatto moltiplicando la sezione per la lunghezza della trave e per il peso specifico del materiale di progetto. Il dimensionamento verrà concluso con la verifica della resistenza della trave calcolato con il nuovo momento flettente, vedendo di conseguenza la sua risposta.

 

3.3_

Per il progetto della trave si è proseguito con l’analisi del carico totale ricavato dall’analisi dei carichi. Questo valore è stato successivamente moltiplicato per l’interasse dell’area che interessava, ricavandosi di conseguenza il carico uniformemente distribuito sulla trave B-B’ presa in esame.

 

q= (qs + qp + qa) *i ⇒ q= (2,700 + 4,303 + 3,000)kN /m² *5,100m

⇒ q= 48,45kN /m

 

Successivamente al calcolo del carico distribuito che insiste sulla trave viene calcolato il momento flettente massimo MMAX che insiste sulla sezione della stessa. Il momento viene calcolato tenendo in considerazione le condizioni di vincolo della trave, e presentando essa una situazione semplicemente appoggiata ad una cerniera a sinistra ed un carrello a destra si può procedere al calcolo del momento massimo flettente mediante la formula:

 

MMAX= (q*L²)/8 ⇒ MMAX= (51,02*5,10²)/8

⇒ MMAX= 165,86kN*m

 

Definito il momento massimo di progetto, si calcola la resistenza di progetto fd e fy, definita dalla motiplicazione della resistenza caratteristica del materiale di progetto (fyk in questo caso CA e fyd nel caso delle barre in acciaio) per il coefficiente di sicurezza αcc (= 0,85) e diviso per il coefficiente di sicurezza γm (= 1,50 per il cls, = 1,15 per l’acciaio), come si può vedere nella formula:

 

fd= αcc*(fyk/γm) ⇒ fd= 0,85*(40/1,50)

⇒ fd= 22,67N/mm²

fy= fyd/γs ⇒ ⇒ fY= 450/1,15

⇒ fY= 391,30N/mm²

 

Ricavate le resistenze di progetto dei due materiali si può procedere per il dimensionamento dell’altezza della trave, la quale presenta una di base di b (= 20 cm), attraverso l’equilibrio alla rotazione della sezione, come si può vedere nella formula:

 

M = C * b* = T * b* ⇒ C = (σca * b * α * hu) / 2

⇒ b* = hu * (1- α/3)

⇒ M = ((σca * b * α * hu) / 2) * (hu * (1- α/3))

⇒ hu = √(M/b) * (1 / (σca/2) * (α * (1- α/3))

⇒ r =  √(1 / (σca/2) * (α * (1- α/3))

⇒ hu = √(M/b) * r

⇒ hu = √(165,86*10⁶) / (20 * 10)) * 2,26

⇒ hu = 432mm

 

Successivamente al calcolo delle resistenze di progetto si calcola il coefficiente α di omogeneizzazione della sezione in C.A. per poter calcolare la posizione dell’asse neutro della sezione viene usato il teorema dei triangoli simili, mediante la formula:

 

xc / hu = (σca/Eca) / (σca/Eca + σfd/Efd) ⇒ hu * (σca/Eca) = xc * (σca/Eca + σfd/Efd)

⇒ xc = (hu * (σca/Eca)) / (σca/Eca + σfd/Efd)

⇒ xc = (hu * (σca/Eca)) / (1/Eca) * (σca + (Eca/Efd) * σfd)

⇒ xc = (hu * σca) / (σca + (Eca/Efd) * σfd)

⇒ n = Eca/Efd ⇒ n = 15

⇒ xc = (hu * σca) / (σca + n * σfd)

⇒ α =  σca / (σca + n * σfd)

⇒ α =  22,67 / (22,67 + (15 * 391,30))

⇒ α =  0,46

⇒ xc = hu * α

⇒ xc = 432 * 0,46

⇒ xc =  198,7mm

 

In ultimo viene definita l’altezza definitiva della sezione sommando all’altezza utile della trave hu (= 432mm) il parametro δ (= 50 mm), che comprende il copriferro e metà barra di acciaio, come si può vedere nella formula:

 

h= hu + δ ⇒ h= 432 +50

⇒ h= 482mm

⇒ h’= 60cm

Verrà quindi adottata una trave avente base b (= 20cm) ed altezza h (= 60cm).

 

4.3_

Per verificare che il progetto della trave sia corretto in toto si procede con il calcolo del peso proprio della trave, il quale peso verrà aggiunto alla fase dell’analisi dei carichi, con i quali verrà ricavato un nuovo momento massimo che verificherà la resistenza della trave.

 

_carichi strutturali_qs

_solaio in latero-cemento 2,700 kN/m²

_trave in c.a 2,790 kN/m²

----------------------------------------------------------------------------------------------------

_totale c.s 5,4900 kN/m²

 

_carichi permanenti_qp

_incidenza tramezzi 0,500 kN/m²

_incidenza impianti 1,000 kN/m²

_pavimento in resina 0,003 kN/m²

_massetto in cs allegerito 1,000 kN/m²

_muro di tamponamento in tufo 1,800 kN/m²

-----------------------------------------------------------------------------------------------------

_totale c.p 4,303 kN/m²

 

_carichi accidentali_qa

_ambiente uffici 3,000 kN/m²

-----------------------------------------------------------------------------------------------------

_totale c.a 3,000 kN/m²

-----------------------------------------------------------------------------------------------------

_totale 12,793 kN/m²

 

verifica del momento massimo effettivo

 

MMAX= (q*L²)/8 ⇒ MMAX= (65,24*5,10²)/8

⇒ MMAX= 212,13kN*m

 

M = C * b* = T * b* ⇒ hu = √(M/b) * r

⇒ hu = √(212,13*10⁶) / (30 * 10)) * 2,26

⇒ hu = 399mm

 

h= hu + δ ⇒ h= 399mm +50

⇒ h= 449mm

⇒ h’= 45cm

Considerando questo nuovo momento massimo la trave non risulta verificata, quindi si sceglie di aumentare la dimensione della base b (= 30cm) ricavandoci di conseguenza un’altezza utile hu (= 39,9cm) e quindi l’altezza complessiva h (= 45cm).

 

5.3_

dati di progetto e tabella

 

 

interasse (m)	qs (KN/m2)	qp (KN/m2)	qa (KN/m2)	q (KN/m)	luce (m)	M (KN*m)
5,1	2,700	4,303	3,00	51,02	5,1	165,86
5,1	5,490	4,303	3,00	65,24	5,1	212,13

 

 

 

alfa	r	b (cm)	h (cm)	delta (cm)	H (cm)	H/l	area (m2)	peso (KN/m)
0,46	2,27	20,0	43,2	5	48,20	0,094	0,10	2,41
0,46	2,27	30,0	39,9	5	44,90	0,088	0,13	3,37