ESERCITAZIONE III: Progettazione di un solaio
ABSTRACT: Obiettivo dell'esercitazione è la progettazione di un solaio con stratigrafia affine a quella tradizionale romana. Approntato un semplice progetto strutturale in pianta relativo a una superficie di 80mq, saranno valutati i carichi per area di influenza della trave soggetta a maggiore sforzo. Infine sarà effettuato il dimensionamento della trave in legno e un confronto con la corrispettiva in acciaio e cemento.
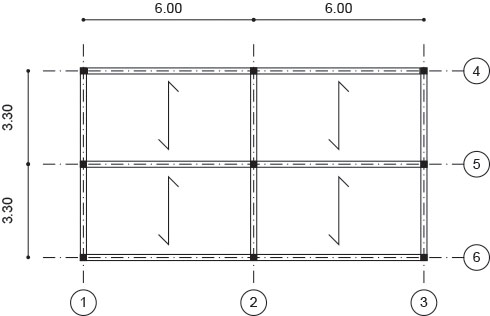
PIANTA
STRATIGRAFIA
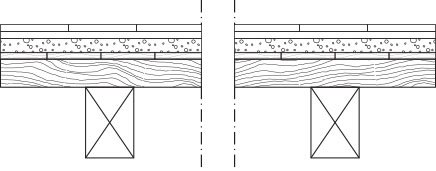
|
Pavimento mattonato |
2.5cm |
| Allettamento | 2.5cm |
|
Massetto di detriti |
5.0cm |
| Tavolato | 2.2cm |
|
Travicelli interas. 50cm |
10.0cm |
| Travi | ? cm |
dal Manuale del Recupero di Roma p. 216
| Carichi permanenti qp | ||
| Pavimento mattonato | 0.025m x 1800 daN/m3 | 45 daN/m2 ⇒ 0.45 KN/m2 |
| Allettamento | 0.025m x 1900 daN/m3 | 47 daN/m2 ⇒ 0.47 KN/m2 |
| Massetto di detriti | 0.050m x 1600 daN/m3 | 80 daN/m2 ⇒ 0.80 KN/m2 |
| Pareti divisorie | (carico diffuso) | 80 daN/m2 ⇒ 0.80 KN/m2 |
| TOTALE | 2.52 KN/m | |
|
Carichi strutturali qs |
||
| Tavolato | 0.022m x 700 daN/m3 | 15 daN/m2 ⇒ 0.15 KN/m2 |
| Travicelli | 0.010m x 0.09m x 1800 daN/m3 / 0.50m | 13 daN/m2 ⇒ 0.13 KN/m2 |
| TOTALE | 0.28 KN/m2 | |
|
Carichi strutturali qs |
||
| Uffici | 3.00 KN/m2 | |
|
|
||
| TOTALE | 5.8 KN/m2 | |
Chiaramente le travi con un'area di influenza con intensità maggiore sono le 1,2-5 e 2,3-5 perciò il carico distribuito sulla trave sarà 5.8 KN/m2 x 3.3 m = 19.14 KN/m
Possiamo dunque realizzare il progetto a momento flettente per una trave doppiamente appoggiata con carico distribuito noto.
Il momento flettente massimo è ql2/8: ne segue che Mmax = 86.13 KN*m
Contrariamente a quanto suggerito dal Manuale del Recupero si opta per una più tecnologica trave lamellare il cui coefficiente di sicurezza fm,k è 24 N/mm2. Alla struttura viene assegnato un coefficiente di kmod variabile di media durata pari a 0.6.
Attraverso questi dati è possibile ricavare l'altezza della trave con un processo progettuale a ritroso dove fm,k viene opportunamente ridotto di un coefficiente ɣm 1.45 è funge da valore di resistenza massimo.
Il momento d'inerzia per una trave a sezione rettangolare e bh3/12 e attraverso Navier σmax= MMAX/Wx da cui segue Wx= I / (h/2)
Assegnamo alla trave una base di 25cm e σmax = fm,k
h=√(6 ql2/ (8*b*σmax) ) = √( 6 . 5.8 KN/m2 . 36m2 / (8*0.25m*9.93/1000 KN/m2))=
= 0.4516 m
Il che vuol dire che dobbiamo aumentare ragionevolmente la sua altezza. Scegliamo una sezione con altezza 50cm
Osserviamo che il coefficiente ɣm 1.45 aggrava molto la scelta della trave: come già accennato a lezione nei paesi nordici dove la tradizione del legno è più consolidata esso è 1.1-1.2 KN/m2 che porta a ridurre l'altezza della trave (in questo caso) a 40-45 cm.
Attraverso il foglio di calcolo fornito effettuiamo dei confronti sulle altezze dei profili per valutare le differenze sulle sezioni così come la normativa consente di calcolarle.
Con logica analoga a quella del calcolo svolto (con le dovute differenze, specialmente nel calcolo del cemento armato) e attraverso l'inserimento di valori di resistenze caratteristiche di materiali mediamente prestazionali giungiamo ai seguenti risultati (a parità di carico):
ACCIAIO fy,k = 235 N/mm2 ⇒ Wx min=749.31 cm3 ⇒ IPE 360
CLS fy 450 N/mm2, Rck 40 N/mm2, b=25cm , copriferro = 5cm⇒H min=32.82 cm ⇒ H=35cm
