Esercitazione 1_Trave reticolare

TRAVE RETICOLARE 2D

Uno dei metodi per superare grandi luci è quello di utilizzare TRAVI RETICOLARI; tali strutture sono costituite da ASTE ognuna soggetta solamente a SFORZO ASSIALE (per avere tale condizione le forze esterne devono agire come carico concentrato nei nodi) e collegate per mezzo di CERNIERE INTERNE in modo da formare TRIANGOLI; la forma triangolare permette di creare strutture che non si deformano dove rimangono però 3 GDV liberi (GDL= 3x3=9  GDV=3x2=6) che devono essere assegnati a vincoli esterni (cerniera e carrello), per questo motivo la trave reticolare nel suo complesso può essere considerata come una trave appoggiata.

Analizziamo ora una trave reticolare composta da 8 campate con un carico concentrato pari a F in ciascuno dei nodi superiori.

Come abbiamo detto precedentemente la trave reticolare può essere ricondotta ad uno SHEMA ISOSTATICO EQUIVALENTE di trave doppiamente appoggiata in modo da ottenere le reazioni vincolari.

R_ua = 0                          R_ub = 0

R_va + R_vb = 9F => R_va = R_vb = 9F/2

Abbiamo quindi determinato le reazioni vincolari esterne, ora dobbiamo determinare le sollecitazioni su ciascuna asta e per farlo possiamo procedere in due modi o con il METODO DEI NODI o con il METODO DELLE SEZIONI DI RITTER.

Il metodo dei nodi consiste nell’analizzare ciascun nodo e le aste ad esso collegate in modo da equilibrare tutte le forze che agiscono su di esso, il problema di tale metodo è che non si possono avere più di un’incognita nella stessa direzione (considerando anche le componenti di forze inclinate).

Il metodo delle sezioni di Ritter invece taglia la struttura in modo da analizzare al massimo tre aste incognite contemporaneamente, facendo attenzione che le aste sezionate non siano collegate allo stesso nodo; avremo a questo punto la trave reticolare divisa in due parti che devono essere in equilibrio, si procede perciò con l’equilibrio alla rotazione di una delle due parti facendo polo in uno dei nodi dove concorrono almeno due aste in modo da non considerare le loro incognite risolvendo un’asta per volta.

Una trave reticolare può essere risolta usando uno solo dei due metodi o entrambi questo permette a volte di velocizzare i passaggi.

Per risolvere questo esercizio possiamo applicare le sezioni di Ritter come in figura e il metodo dei nodi per il nodo 1 e 10 poiché presentando solo aste verticali e orizzontali risulta più immediato, inoltre essendo la struttura simmetrica basta analizzare solo una parte delle aste e poi per simmetria avremo ottenuto l’analisi completa.

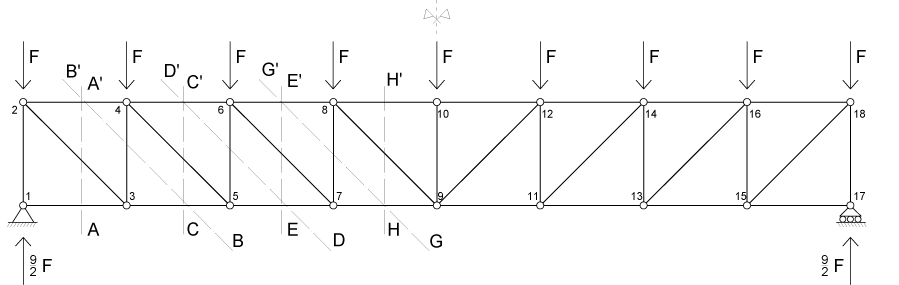
Iniziamo dall’analisi del NODO  1, in esso è presente un’azione esterna verticale e nessuna forza orizzontale, poiché non sono non ci sono aste inclinate l’unica che concorre all’equilibrio è l’ASTA 1-2 che risulta COMPRESSA ed è quindi un PUNTONE mentre l’ASTA 1-3 risulta SCARICA.

 

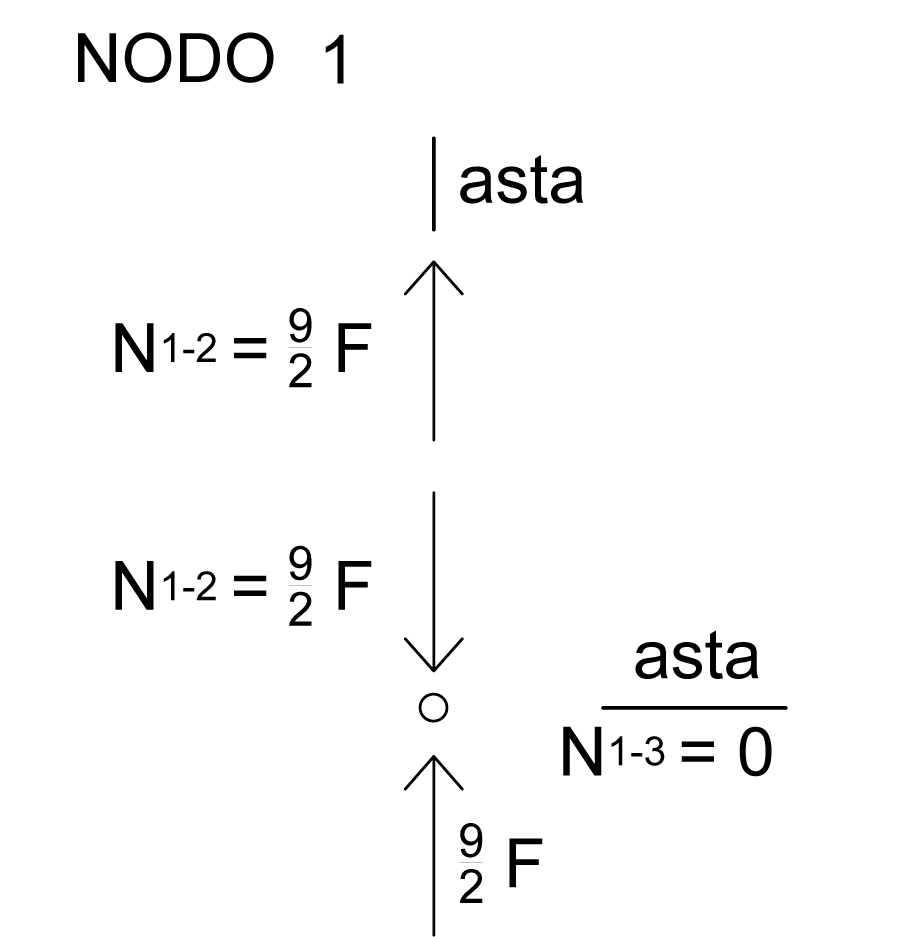
Passiamo ora ad effettuare la prima sezione virtuale (sezione di Ritter) in questo caso la SEZIONE A-A’. Per prima cosa dobbiamo disegnare gli sforzi assiali N che agisco su ciascuna asta, imponendoli di VERSO USCENTE stiamo ipotizzando che le aste sia soggette a TRAZIONE e quindi siano dei TIRANTI, se dai calcoli le forze risultassero negative significa che il verso corretto sia ENTRANTE, che l’asta sia COMPRESSA e di conseguenza un PUNTONE. In questa sezione sappiamo già che l’asta 1-3 è scarica quindi ci concentreremo solo sulle altre due aste sezionate avendo come incognite N_2-3 e N_2-4.

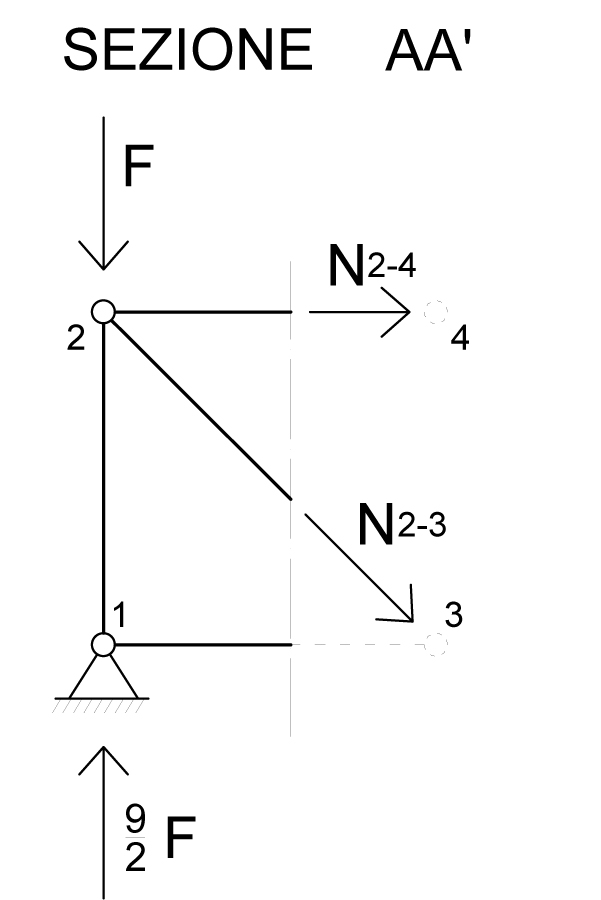
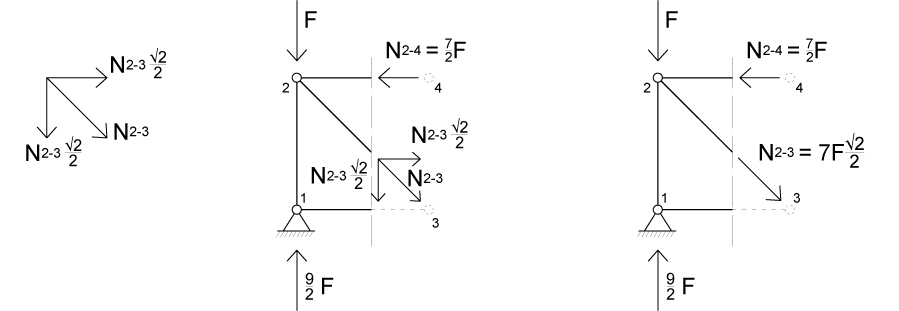
Facciamo l’equilibrio alla rotazione con polo nel nodo 3 (la forza N_2-3 ha braccio nullo quindi non sarà presa in considerazione) e potremmo ricavarci N_2-4.

N_2-4 risulta negativa ed è quindi un PUNTONE.

Per conoscere N_2-3 possiamo fare l’equilibrio alla traslazione orizzontale, prima però dobbiamo scomporre la forza nei suoi 2 vettori componenti, in questo caso pari entrambi a N_2-3(√2/2)poiché l’asta è inclinata di 45°.

N_2-3 risulta positiva ed è quindi un TIRANTE.

 

Continuiamo con la SEZIONE B-B’ questo risulta essere un caso particolare, per determinare N_3-5 potremmo fare sia l’equilibrio alla rotazione con polo nel nodo 4 sia l’equilibrio alla traslazione orizzontale poiché è l’unica forza orizzontale incognita, optiamo per la seconda perché immediata.

N_3-5 risulta positiva ed è quindi un TIRANTE.

Per ottenere N_3-4 possiamo fare l’equilibrio alla traslazione verticale.

N_3-4 risulta negativa ed è quindi un PUNTONE.

Analizziamo ora la SEZIONE C-C’. Per ottenere N_4-6 facciamo l’equilibrio alla rotazione con polo nel nodo 5.

N_4-6 risulta negativa ed è quindi un PUNTONE.

Per ricavare N_4-5 basta fare l’equilibrio alla traslazione orizzontale come per il caso di N_2-3.

N_4-5 risulta positiva ed è quindi un TIRANTE.

Nella SEZIONE D-D’ possiamo scegliere, come nella sezione B-B’, indifferentemente come procedere; per ricavarci N_5-7 facciamo l’equilibrio alla traslazione orizzontale.

N_5-7 risulta positiva ed è quindi un TIRANTE.

Con l’equilibrio alla traslazione verticale ricaviamo N_5-6.

N_5-6 risulta negativa ed è quindi un PUNTONE.

Nella SEZIONE E-E’. Per ottenere N_6-8 facciamo l’equilibrio alla rotazione con polo nel nodo 7.

N_6-8 risulta negativa ed è quindi un PUNTONE.

Per ricavare N_6-7  basta fare l’equilibrio alla traslazione orizzontale.

N_6-7 risulta positiva ed è quindi un TIRANTE.

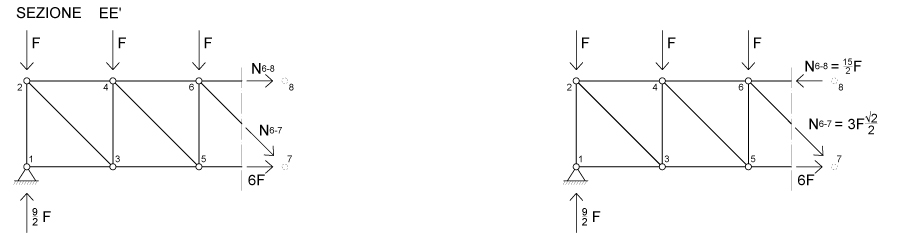
Nella SEZIONE G-G’ per ricavare N_7-9 possiamo fare l’equilibrio alla traslazione orizzontale.

N_7-9 risulta positiva ed è quindi un TIRANTE.

per ricavare N_7-8 possiamo fare l’equilibrio alla traslazione verticale.

N_7-8 risulta negativa ed è quindi un PUNTONE.

Nella SEZIONE H-H’. Per ottenere N_8-10 facciamo l’equilibrio alla rotazione con polo nel nodo 9.

N_8-10 risulta negativa ed è quindi un PUNTONE.

Per ricavare N_8-9  basta fare l’equilibrio alla traslazione orizzontale.

N_8-9 risulta positiva ed è quindi un TIRANTE.

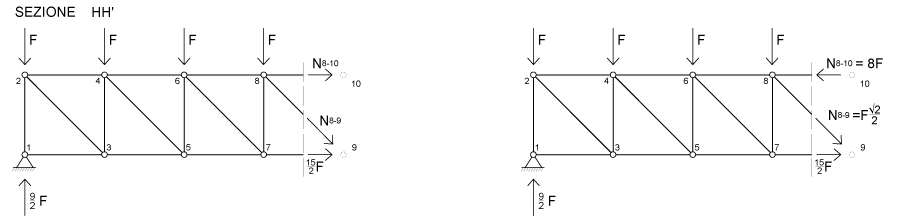
Abbiamo così risolto la parte sinistra della trave reticolare ed ora per simmetria possiamo conoscere gli sforzi assiali delle aste nella parte destra. Rimane da analizzare solo l’asta centrale e per comodità utilizzeremo il metodo dei nodi.

Osservando il NODO 10 possiamo vedere che l’unica forza incognita è N_9-10 che deve equilibrare la forza esterna F, l’asta sarà quindi un PUNTONE con N_9-10 = F.

 

Possiamo ora verificare i nostri calcoli ricorrendo a SAP.

Per prima cosa dobbiamo crere un nuovo file per poter disegnare la trave reticolare in esame FILE > NEW MODEL > GRIND ONLY ricordandoci di utilizzare le unità di misura corrette (kN, m, °C).

Impostiamo 9 spazi lungo x e 2 lungo z, con una lunghezza L unitaria.

Successivamente si impostano i vincoli attraverso il comando ASSIGN  > JOINT RESTRAINTS ricordandosi di assegnare un carrello ed una cerniera in modo da ottenere un sistema isostatico.

Nella trave reticolare tutti i vincoli interni sono cerniere e non incastri come da default di SAP, dobbiamo quindi rilasciare il momento a destra e a sinistra di ogni nodo, per farlo andiamo in ASSIGN > FRAME > RELEASE > MOMENT 3-3(MAJOR) > START 0 – END 0.

Bisogna ora impostare che il peso proprio dell’asta non venga considerato in fase di calcolo, andando ad aggiungere ai “load patterns” uno che abbia lo 0 alla voce “self weight multiplier”andiamo quindi su DEFINE > LOAD PATTERNS > ADD NEW LOAD PATTERNSe impostiamo come SELF WEIGHT MULTIPLIER = 0.

Ora bisogna assegnare il carico e per farlo selezioniamo i nodi superiori e ricorriamo al comando ASSIGN  > JOINT LOADS > FORCES impostiamo un carico puntuale su ognuno di essi di -10 KN.

Possiamo ora lanciare il calcolo e visionare il diagramma di SFORZO ASSIALE.

Possiamo constatare che i calcoli a mano risultano corretti.

 

 

 

TRAVE RETICOLARE 3D

Per aiutarci nella modellazione si è scelto di ricorrere ad Autocad.

Si è quindi disegnata una trave reticolare spaziale di lunghezza 3L, larghezza 2L e altezza L (con L=2m), con l’accortezza di non utilizzare polilinee (poiché il reticolo è composto da aste singole) e utilizzare un layer diverso da quello di default (che non viene letto da SAP). Dopodiché basta salvare in formato DXF 2000 (DXF più recenti non garantiscono la compatibilità).

Ora da SAP dobbiamo importare il DXF precedentemente creato. Per fa ciò dobbiamo utilizzare il comando FILE > IMPORT > AUTOCAD.DXF FILE ricordandoci di utilizzare le unità di misura corrette (kN, m, °C) e di impostare in Frames "cad" dal menù a tendina in modo che vengano lette le aste.

Fatto ciò selezioniamo l’intero reticolo ed usiamo EDIT > EDIT POINT  > MERGE JOINTS  >  MERGE TOLERANCE  >  0,01 (per  impostare un errore nella giunzione delle aste di 1 cm).

Successivamente si impostano i vincoli attraverso il comando ASSIGN  > JOINT RESTRAINTS ricordandosi di utilizzare cerniere e carrelli in modo che non giacciano sullo stesso asse.

Ora bisogna assegnare un materiale ed un profilo alle aste. Dopo aver selezionato tutte le aste, clicchiamo su DEFINE > SECTION PROPERTIES > FRAME SECTIONS si è scelto di utilizzare un tubolare in acciaio da 100x5. Successivamente si devono selezionare tutte le aste e bisogna assegnargli il profilo precedentemente creato utilizzando il comando ASSIGN   > FRAME  > FRAME SECTIONS.

Ora bisogna assegnare il carico e per farlo selezioniamo i 12 nodi superiori e ricorriamo al comando ASSIGN  > JOINT LOADS > FORCES impostiamo un carico puntuale su ognuno di essi di -40 KN (si è scelto questo valore tenendo conto dell’area di incidenza del solaio superiore e il segno negativo serve a dargli la direzione verso il basso).

Bisogna ora impostare che il peso proprio dell’asta non venga considerato in fase di calcolo, andando ad aggiungere ai “load patterns” uno che abbia lo 0 alla voce “self weight multiplier”andiamo quindi su DEFINE > LOAD PATTERNS > ADD NEW LOAD PATTERNS.

Dato che in una struttura reticolare tutti i vincoli interni sono cerniere, dobbiamo fare un’operazione di rilascio del momento ASSIGN > FRAME > RELEASE > MOMENT 3-3(MAJOR) > START 0 END 0 altrimenti verrebbero considerati incastri e ciè falserebbe i risultati.

Prima di lanciare il calcolo dobbiamo poter riconoscere le aste i cui valori verranno tabellati per far ciò andiamo in SET DISPLAY OPTIONS > FRAMES/CABLES/TENDONS >spuntiamo LABELS.

 

Rimane solamente da lanciare il calcolo. Per farlo andiamo in RUN ANALYSIS > disattiviamo le voci MODAL E DEAD e clicchiamo RUN NOW.

 

La prima cosa che mostra il software è la deformata.

Per visualizzare le reazioni vincolari invece dobbiamo andare in SHOW FORCES/STRESSES > JOINTS.

Per visualizzare gli sforzi assiali (unici presenti) usiamo il comando SHOW FORCES/STRESSES > FRAME/CABLES > AXIAL FORCE.

Possiamo ottenere le tabelle con gli sforzi assiali nelle aste con il comando DISPLAY > SHOW TABLES > spuntiamoANALYSIS RESULTS > ELEMENT FORCES – FRAMES.