commenti

Correzione tavola 6

1 anno 9 mesi fa
diagrammi graticcio

5 anni 6 mesi fa
ultima domanda

5 anni 6 mesi fa
no ho ancora un'ultima

5 anni 7 mesi fa
sì sì tutto chiaro.

5 anni 7 mesi fa

Commenti recenti

Correzione tavola 6 1 anno 9 mesi fa
diagrammi graticcio 5 anni 6 mesi fa
ultima domanda 5 anni 6 mesi fa
no ho ancora un'ultima 5 anni 7 mesi fa
sì sì tutto chiaro. 5 anni 7 mesi fa
Load Pattern peso proprio 5 anni 7 mesi fa
Ciao Fabiana, 5 anni 7 mesi fa
Ciao Giuliana, 5 anni 7 mesi fa
Modellazione setto - Giuliana Nardi 5 anni 7 mesi fa
assegnare sezione a setti su sap 5 anni 7 mesi fa

Esercitazione 2_Trave iperstatica (metodo della linea elastica)

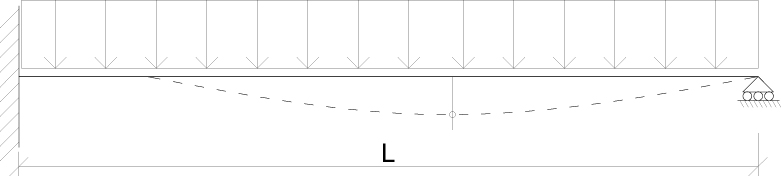
Inviato da lorenzo.procaccini il Sab, 13/04/2013 - 22:07

Per risolvere questa trave iperstatica si ricorre al metodo d’integrazione della linea elastica che ci permette di ottenere l’incognita richiesta, cioè lo spostamento verticale massimo vs della deformata.

Iniziamo analizzando le 8 equazioni fondamentali:

- 3 eq. di EQUILIBRIO

$\left\{\begin{matrix}N'+q_{1}=0 & & \\ T'+q_{2}=0 & & \\ M'+T=0 & & \end{matrix}\right.$

- 3 eq. di CONGRUENZA

$\left\{\begin{matrix}\varepsilon=u' & & \\ \varphi =v' & & \\ \chi =\varphi ' & & \end{matrix}\right.$

-2 eq. del LEGAME COSTITUTIVO

$\left\{\begin{matrix}N=EA\varepsilon & & \\ M=EI\chi & & \end{matrix}\right.$

Si prendo in analisi le 5 equazioni che sono legate allo spostamento vs che sono:

⎧(dT/ds) + q₂=0

⎢(dM/ds) + T=0

⎨M=E*I*χ

⎢χ=(dφ/ds)

⎩φ=(dv/ds)

Ora bisogna ottenere da queste equazioni v in funzione di s, per far ciò bisogna eseguire i questi passaggi:

sapendo che:

$\frac{dT}{ds}+q_{2}=0$ e $T=-\frac{dM}{ds}$

sostituendo otteniamo:

$\frac{d}{ds}\left ( -\frac{dM}{ds} \right )+q_{2}=0$ $-\frac{d^{2}M}{ds^{2}}+q_{2}=0$ $\frac{d^{2}M}{ds^{2}}=q_{2}$

sapendo che:

$\chi =\frac{d\varphi }{ds}$ $\varphi =\frac{dv}{ds}$ $\chi =\frac{d}{ds}\left ( \frac{dv}{ds} \right )=\frac{d^{2}v}{ds^{2}}$

sostituendo otteniamo:

$M=EI\chi =EI\frac{d^{2}v}{ds^{2}}$ $\frac{d^{2}}{ds^{2}}\left ( EI\frac{d^{2}v}{ds^{2}} \right )=q_{2}$ $EI\frac{d^{4}v}{ds^{4}}=q_{2}$

otteniamo così l'EQUAZIONE DELLA LINEA ELASTICA

$\frac{d^{4}v}{ds^{4}}=\frac{q_{2}}{EI}$

Svolgiamo ora le opportune integrazioni:

$\frac{d^{3}v}{ds^{3}}=\frac{q_{2}}{EI}s+C_{1}$

$\frac{d^{2}v}{ds^{2}}=\frac{q_{2}}{EI}\frac{s^{2}}{2}+C_{1}s+C_{2}$

$\frac{dv}{ds}=\frac{q_{2}}{EI}\frac{s^{3}}{6}+C_{1}\frac{s^{2}}{2}+C_{2}s+C_{3}$

$v\left ( s \right )=\frac{q_{2}}{EI}\frac{s^{4}}{24}+C_{1}\frac{s^{3}}{6}+C_{2}\frac{s^{2}}{2}+C_{3}s+C_{4}$

Passiomo ora ad analizzare le condizioni al bordo dalle quali si ottiene:

- nell'incastro all'estremo sinistro dove s=o si ha v(0)=0 e $\varphi \left ( 0 \right )=0$ da cui si ricava C₃=0 e C₄=0

- nel carrello all'estremo destro dove s=l si ha:

- $v\left ( l \right )=0$ da cui si ottiene $v\left ( l \right )=-\frac{ql^{4}}{24EI}+C_{1}\frac{l^{3}}{6}+C_{2}\frac{l^{2}}{2}=0$

- $M\left ( l \right )=0$ sapendo che M=E*I*χ; possiamo cosiderare solo la curvatura perchè E ed I sono costanti

$M\left (l \right )=-\frac{ql^{2}}{2EI}+C_{1}l+C_{2}=0$

Mettendo quindi a sistema queste due equazioni e risolvendo si ha:

$C_{2}=\frac{q_{2}l^{2}}{2EI}-C_{1}l$ $-\frac{q_{2}l^{4}}{24EI}+C_{1}\frac{l^{3}}{6}+\left ( \frac{q_{2}l^{2}}{2EI}-C_{1}l \right )\frac{l^{2}}{2}=0$

$-\frac{q_{2}l^{4}}{24EI}+C_{1}\frac{l^{3}}{6}+ \frac{q_{2}l^{4}}{4EI}-C_{1} \frac{l^{3}}{2}=0$

$-\frac{q_{2}l^{4}+6q_{2}l^{4}}{24EI}+C_{1}\frac{l^{3}-3C_{1}l^{3}}{6}=0$

$\frac{5q_{2}l^{4}}{24EI}-\frac{C_{1}l^{3}}{3}=0$

$C_{1}=\frac{5q_{2}l^{4}}{24EI}*\frac{3}{l^{3}}=\frac{5}{8}\frac{q_{2}l}{EI}$

$C_{2}=\frac{q_{2}l^{2}}{2EI}-\left ( \frac{5q_{2}l}{8EI} \right )l=\frac{4q_{2}l^{2}-5q_{2}l^{2}}{8EI}=-\frac{q_{2}l^{2}}{8EI}$

Ora dobbiamo determinare per quale valore di s si ha v_max. Sapendo che all’abbassamento verticale massimo corrisponde un valore nullo della derivata della funzione che approssima la deformata della trave è sufficiente, quindi, derivare la funzione v_(s)e trovare i valori di s per i quali la derivata si annulla.

$\varphi =\frac{dv}{ds}=-\frac{q_{2}s^{3}}{6EI}+C_{1}\frac{s^{2}}{2}+_{2}s+C_{3}$

Si ottiene un'equazione di 3° grado dove dobbiamo sostituire i valori di C ottenuti precedentemente.

$\varphi =-\frac{q_{2}s^{3}}{6EI}+\frac{5q_{2}ls^{2}}{16EI}-\frac{q_{2}l^{2}s}{8EI}=0$

$\varphi =s\left ( -\frac{q_{2}s^{2}}{6EI}+\frac{5q_{2}ls}{16EI}-\frac{q_{2}l^{2}}{8EI} \right )$

si ha quindi come prima soluzione $s=0$

$s=\left ( \frac{5q_{2}l^{2}}{16EI}\pm \sqrt{\frac{25q_{2}l^{2}}{256E^{2}I^{2}}-4\frac{q{_{2}}^{2}l^{2}}{48E^{2}I^{2}}} \right )*\frac{3EI}{q_{2}}$

Ipotizzando una trave di lunghezza unitaria (l=1) e risolvendola otteniamo s=1,296 (non accettabile poichè esterno alla trave) e s=0,5784.

Possiamo ora calcolarci lo spostamento massimo:

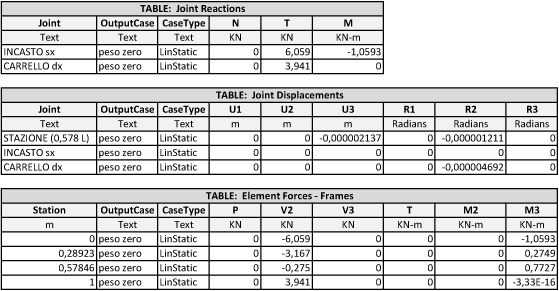
$v\left ( 0,57 \right )=\frac{q_{2}\left ( 0,57 \right )^{4}}{24EI}+\frac{5q_{2}l\left ( 0,57 \right )^{3}}{48EI}-\frac{q_{2}l\left ( 0,57 \right )^{2}}{16EI}=-\frac{0,25q_{2}l^{2}}{48EI}$

$l=1\rightarrow v\left ( 0,57 \right )=-0,00536\frac{q_{2}}{EI}$

Utilizzando le equazioni studiate all'inizio possiamo ottenere i valori di taglio e momento in punti noti:

$M=EI\frac{d^{2}v}{ds^{2}}=-\frac{q_{2}s^{2}}{2}+\frac{5q_{2}l}{8}s-\frac{q_{2}l^{2}}{8}$

$M\left ( 0 \right )=-\frac{q_{2}l^{2}}{8}$ $M\left ( l \right )=\frac{q_{2}s^{2}}{2}+\frac{5q_{2}l}{8}s-\frac{q_{2}l^{2}}{8}$

$T=-M\left ( s \right )=q_{2}s-\frac{5q_{2}l}{8}$

$T\left ( 0 \right )=-\frac{5q_{2}l}{8}$ $T\left ( l \right )=q_{2}l-\frac{5q_{2}l}{8}=-\frac{3}{8}q_{2}l$

Rimangono ora i diagrammi:

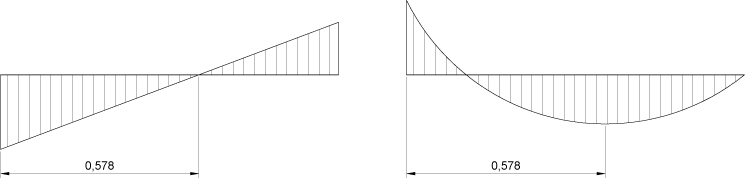
- Il diagramma del taglio ha un andamento lineare e si ha un taglio negativo massimo in prossimità dell’incastro e uno positivo massimo nel carrello destro mentre l’intersezione con l’asse della trave corrisponde a s=0,578.

- Il diagramma del momento ha un andamento parabolico, con un massimo negativo nell’incastro, curvatura verso il basso e valore zero nel carrello mentre si ha il momento massimo positivo ad s=0,578.

VERIFICA IN SAP

Iniziamo creando un nuovo file selezioniamo il preset GRIND ed impostiamo 2 sul numero di assi della griglia lungo x ed e 1 come GRIND SPACING lungo x (in modo da ottenere una trave di lunghezza unitaria come si era ipotizzato nell’esercizio precedente).

Ora si deve disegnare la trave di lunghezza AB ed aggiungere il punto a 0,5784 clicchiamo sul comando DRAW SPECIAL JOINT, selezioniamo il punto A ed impostiamo una distanza 0,5784 sull’offset x.

Si passa all’assegnazione dei vincoli, dopo aver selezionato il punto > ASSIGN > JOINT RESTRAINTS > scegliere il tipo di vincolo ( incastro nel nodo a sinistra, carrello in quello a destra).

Dobbiamo ora togliere il contributo del peso proprio della trave dai carichi, andiamo in DEFINE > LOAD PATTERNS > SELF WEIGHT MULTIPLER = 0 > assegnargli un nome (peso_nullo) > ADD NEW LOAD PATTERN.

Si deve ora assegnare il carico uniformemente distribuito, selezioniamo l’asta ed andiamo in ASSIGN > FRAME LOADS > DISTRIBUTED > selezioniamo la nostra trave di peso nullo ed impostiamo l’unità di misura voluta (nel nostro caso N, m, °C) > nella casella UNIFORM scrivere il carico (-10 KN, negativo poiché verso il basso).

Rimane solamente da lanciare il calcolo. Per farlo andiamo in RUN ANALYSIS > disattiviamo le voci MODAL E DEAD e clicchiamo RUN NOW.

La prima cosa che mostra il software è la deformata.

Per visualizzare il TAGLIO usiamo il comando SHOW FORCES/STRESSES > FRAME/CABLES > SHEAR 2/2.

Per visualizzare il MOMENTO usiamo il comando SHOW FORCES/STRESSES > FRAME/CABLES > MOMENT 3/3.

Dobbiamo ora definire il profilo in ACCIAIO d’assegnare alla trave.

Iniziamo impostando uno scatolare cavo 40x30cm spessore 2mm, andiamo in DEFINE > SECTION PROPERTIES > FRAME SECTIONS ed impostiamo i nostri parametri. Successivamente si deve selezionare l’asta e assegnargli il profilo appena creato utilizzando il comando ASSIGN > FRAME > FRAME SECTIONS.

Fatto ciò possiamo lanciare nuovamente il calcolo e d esportarci le tabelle che si ottengono dall’analisi per farlo andiamo in DISPLAY > SHOW TABLES > spuntiamoANALYSIS RESULTS.

Ottengo così le seguenti tabelle:

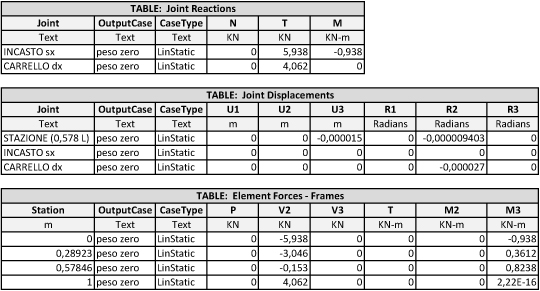
Ripetiamo la stessa procedura, questa volta assegnamo alla trave un profilo in CALESTRUZZO ARMATO h=50cm b=25cm.

SdC(b) (LM PA)

Esercitazione

Blog di lorenzo.procaccini

Menu principale

Tu sei qui

SdC(b)

commenti

Commenti recenti

Maschera di ricerca

Esercitazione 2_Trave iperstatica (metodo della linea elastica)