5_ESERCITAZIONE SUL METODO DELLE FORZE_16-04-2013

ESERCITAZIONE SUL METODO DELLE FORZE_16-04-2013

Il metodo delle forze consente di risolvere strutture iperstatiche in maniera tutto sommato agevole, dal momento che la struttura oggetto d’analisi viene ricondotta ad una struttura isostatica di riferimento. Il concetto chiave di questo procedimento risiede nella nozione di compatibilità cinematica e di congruenza di spostamenti e/o rotazioni semplici, noti negli esempi di sistemi isostatici a cui ci si rifà.

Risolvendo uno degli esempi più comuni di struttura iperstatica, ovvero la trave continua su più appoggi, descriveremo per punti questo metodo di risoluzione.

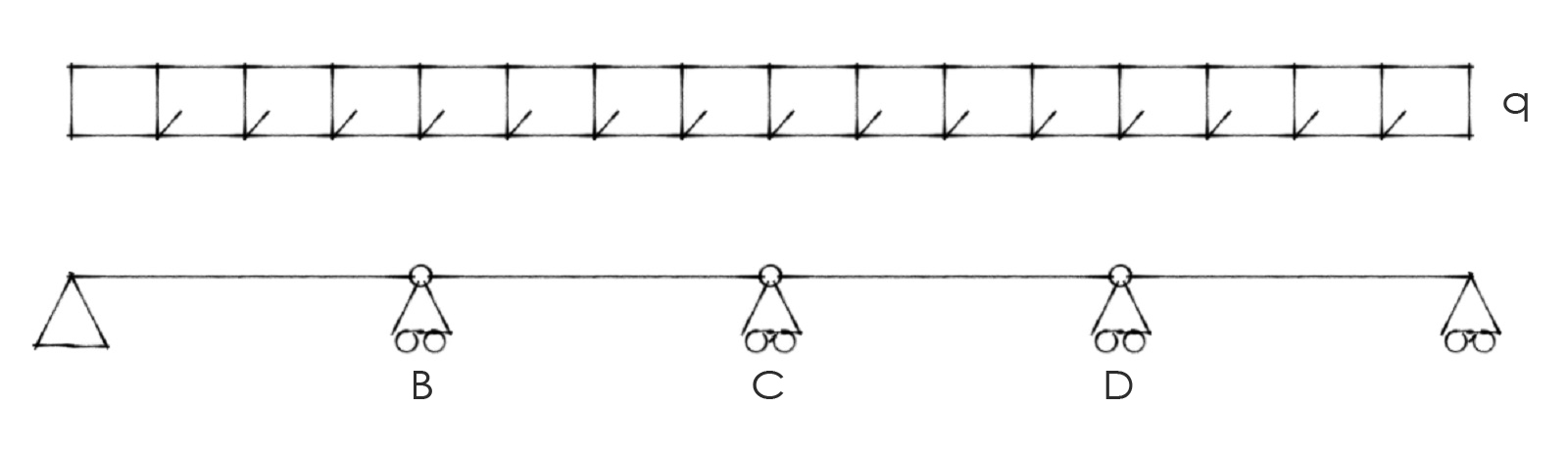
• STRUTTURA IPERSTATICA DI PARTENZA

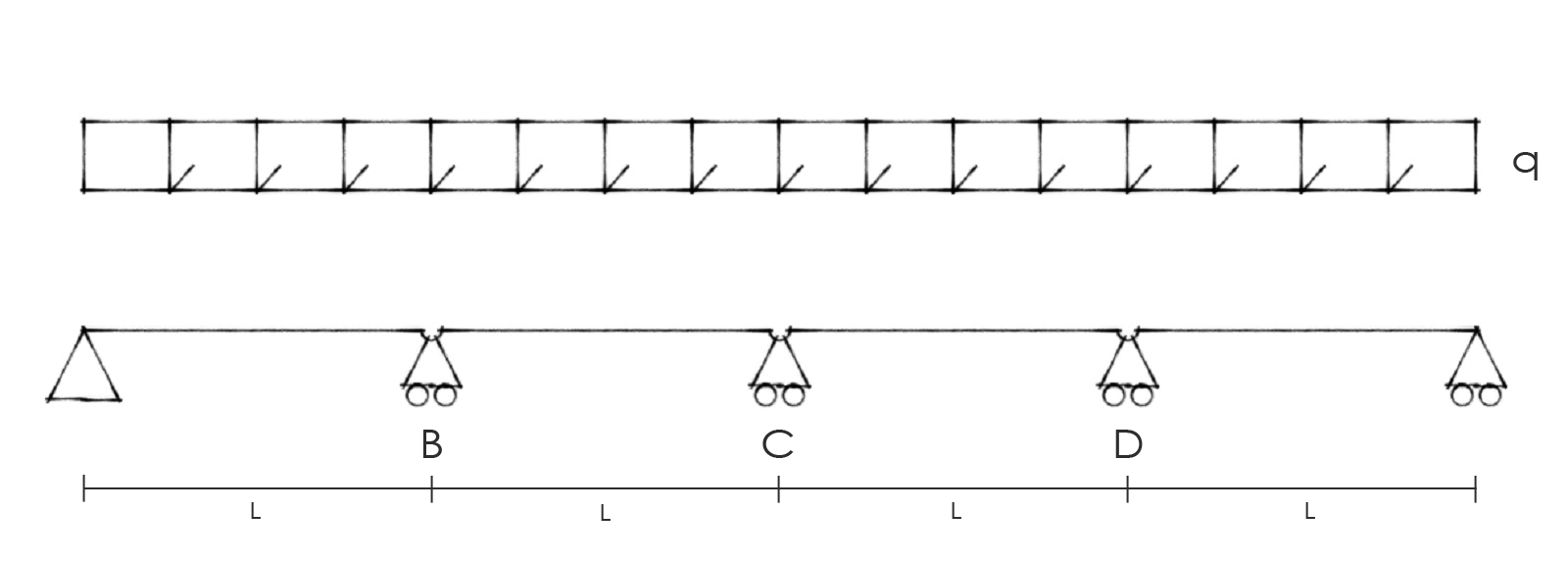
• STRUTTURA ISOSTATICA DI RIFERIMENTO

La struttura iperstatica di partenza viene ricondotta ad una isostatica nella quale, al numero di gradi di iperstaticità precedenti, corrispondono lo stesso numero di reazioni vincolari incognite in grado di non labilizzare la struttura in questione.

Nel nostro caso specifico abbiamo, quindi, 3 reazioni vincolari incognite (per il principio della simmetria x₁=x₃ d’ora in avanti si userà solo x₁) che si oppongono alla rotazione concessa dalle cerniere e precedentemente negata dai 3 vincoli.

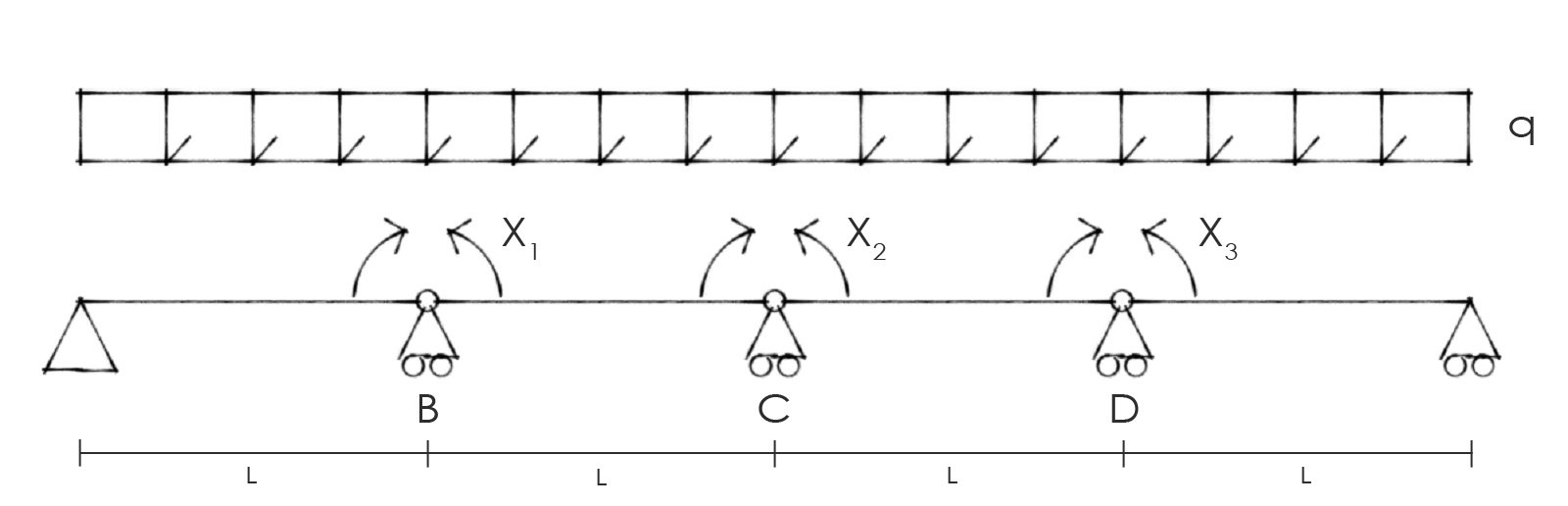
• EQUAZIONI DI COMPATIBILITA’ CINEMATICA

Individuate le reazioni incognite, dobbiamo scrivere le equazioni di compatibilità cinematica capaci di ripristinare il vincolo iperstatico, soppresso attraverso la trasformazione dello stesso in reazione vincolare.

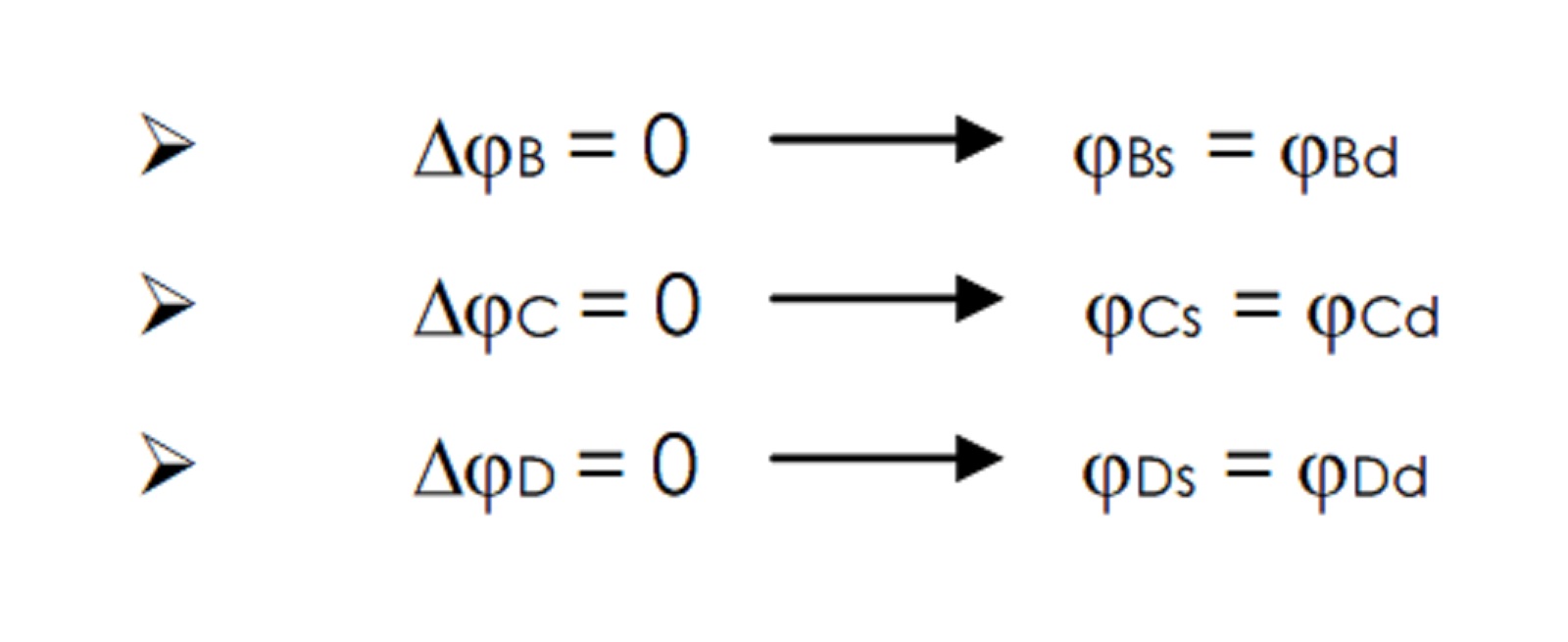
• RISOLUZIONE DELLE EQUAZIONI

Sostituendo alle equazioni di compatibilità cinematica i rispettivi valori delle rotazioni nei 3 nodi B,C e D e mettendole a sistema possiamo trovare i valori delle nostre due incognite x₁ ex_2.

Risolvendo questo sistema di 2 equazioni in 2 incognite troviamo i due valori delle nostre incognite x₁ e x₂.

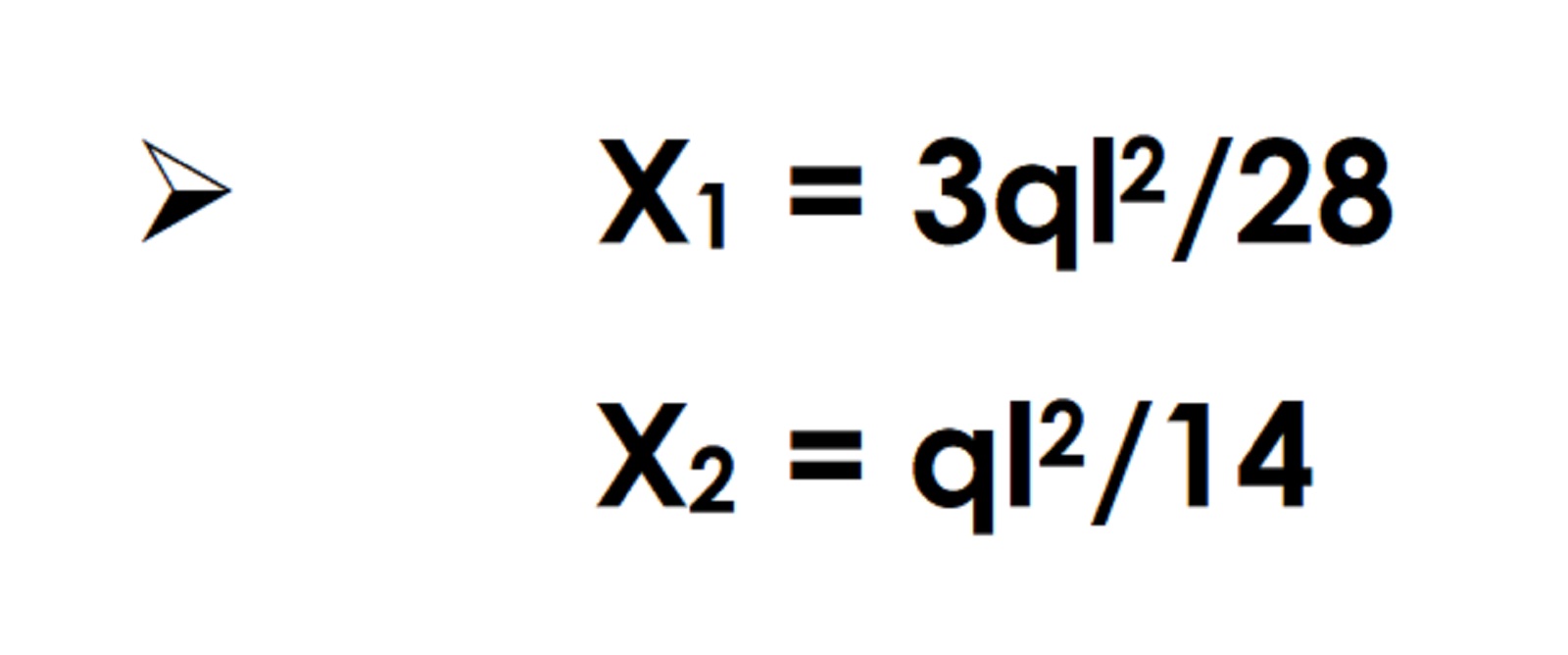
• PRINCIPIO DI SOVRAPPOSIZIONE DEGLI EFFETTI

Definite le incognite delle reazioni vincolari x₁ e x₂ applichiamo in maniera sistematica il principio di sovrapposizione degli effetti, semplificando ulteriormente la struttura isostatica di riferimento mediante due strutture: una dipendente dal carico q e l’altra dipendente dalle reazioni vincolari x.

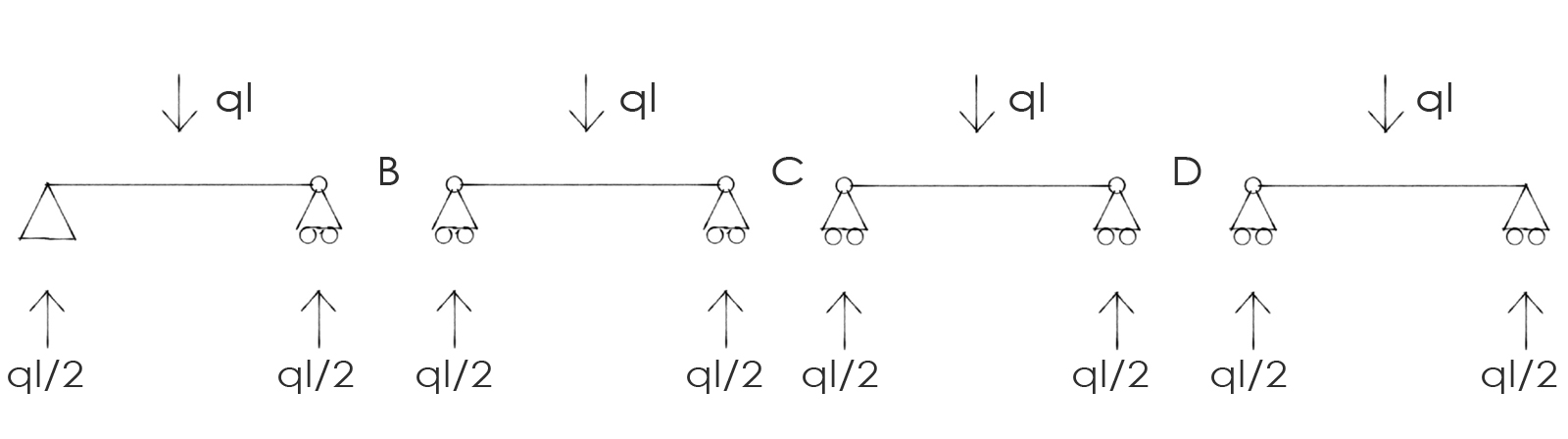
In entrambi i casi è possibile scomporre la struttura in 4 travi doppiamente appoggiate, studiare le reazioni vincolari dovute al carico q e ai momenti x₁ e x₂ in ognuna di queste 4 travi e sommare quelle relative ai medesimi nodi per avere le reazioni vincolari finali dei due sistemi.

q)

x)

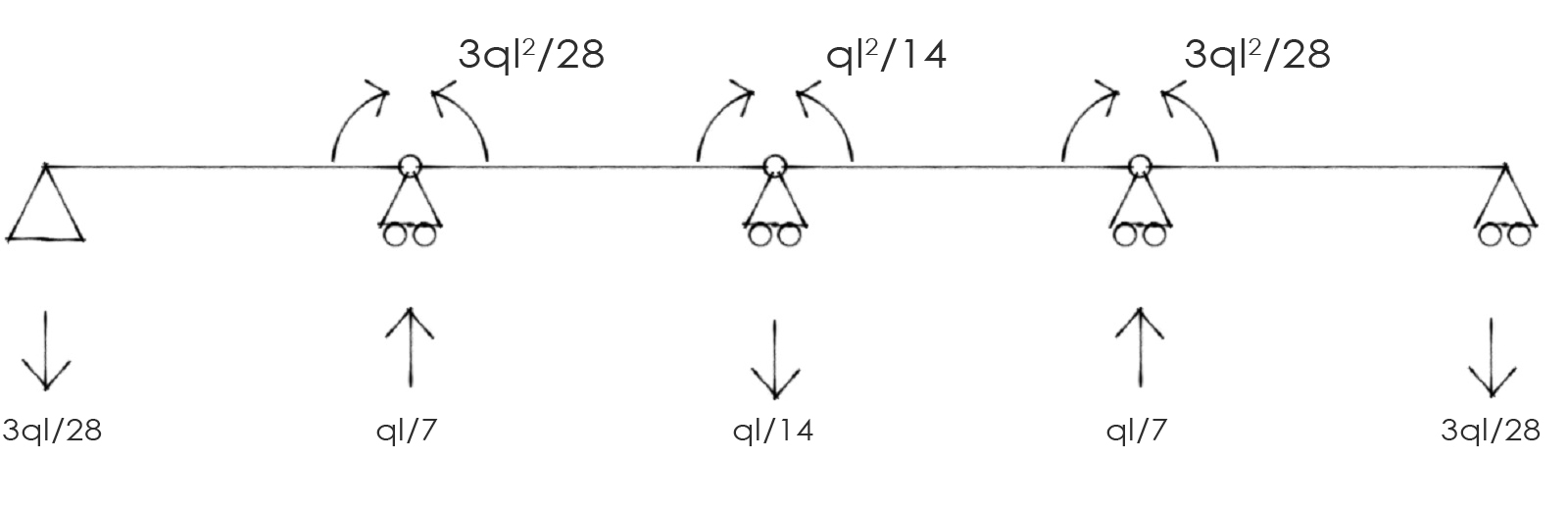
A questo punto è possibile sovrapporre gli effetti dei due sistemi e avere lo schema delle reazioni vincolari della nostra struttura di partenza. Passaggio questo necessario al fine di poter diagrammare lo sforzo di Taglio e il Momento Flettente.

Reazioni vincolari

Taglio

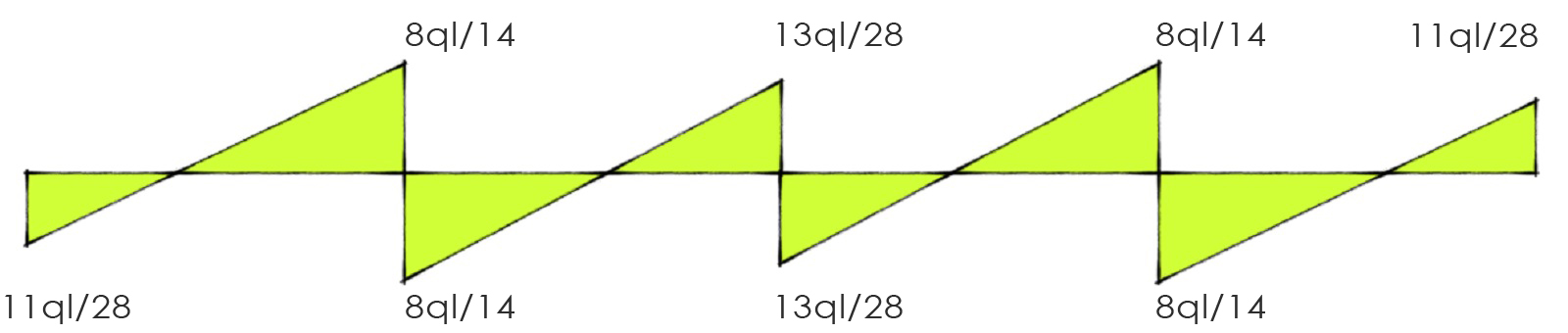
Momento Flettente