Esercitazione: Risoluzione di una struttura iperstatica

Analisi di una trave iperstatica

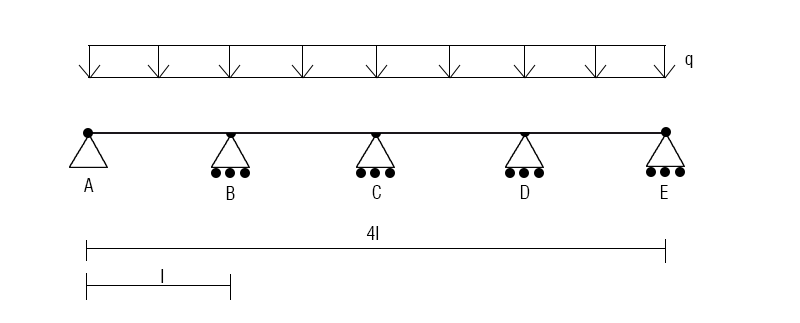
Per risolvere una struttura iperstatica il primo passo è associarla ad una struttura isostatica di riferimento, in questo caso posso considerarla come una serie di travi appoggiate con una coppia di forze che bilanciano i momenti nei nodi interni

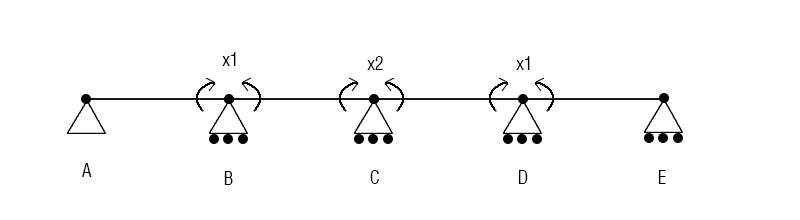
Ora vado ad analizzare le rotazioni nei nodi B, C, D. Visto che la struttura è simmetrica posso considerare i valori della coppia di momenti in B e in D equivalenti

ϕBs = (ql³ / 24EI) –( x₁l / 3EI)
ϕBd = -(ql³ / 24EI) +( x₁l / 3EI) +(x₂l / 6EI)

ϕBs =-ϕDd      ϕBd =-ϕDs      

Il termine +(x₂l / 6EI) che compare in ϕBd sta ad indicare la rotazione generata dal momento x₂ nel polo opposto a quello analizzato ma che incrementa ulteriormente la deformazione della trave ed assume un valore pari alla metà della rotazione generata dal momento x₂ nel suo polo di applicazione C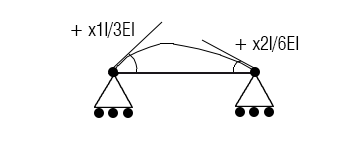

ϕCs  =  (ql³ / 24EI) -(x₂l / 3EI) -( x₁l / 6EI)

ϕCd  = - (ql³ / 24EI) +(x₂l / 3EI) +( x₁l / 6EI)

Ora andremo a stabilire l’uguaglianza tra le rotazioni per equilibrare i momenti e metteremo a sistema due coppie di rotazioni per ricavare le incognite

ϕBs =ϕBd     ϕDs =ϕDd     ϕCs  =  ϕCd     (considero ne sistema le coppie B e C)

(ql³ / 24EI) –( x₁l / 3EI)  =  -(ql³ / 24EI) +( x₁l / 3EI) +(x₂l / 6EI)
(ql³ / 24EI) -(x₂l / 3EI) -( x₁l / 6EI)  =   - (ql³ / 24EI) +(x₂l / 3EI) +( x₁l / 6EI)

Dalla prima ricavo x1:    -(2 x₁l / 3EI) = -(ql³ / 12EI) +(x₂l / 6EI)
x₁ = (ql²/8) – (x₂/4)

Ora sostituisco la x₁ trovata nella seconda equazione per trovare l’unica incognita x_2:
(ql³ / 24) = (7x₂l/12)       quindi    x2 = (ql²/14)

Conoscendo il valore di x₂ lo andrò a sostituire nuovamente per ricavare il valore di x₁
(ql³/12) – (ql³/21) = (x₁l/3)       quindi    x1 = (3ql²/28)

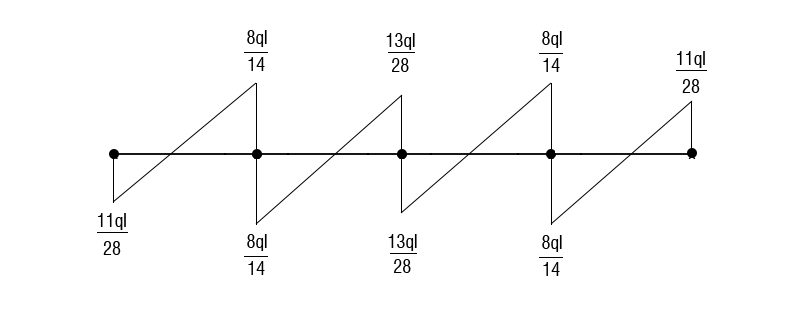
Ora sovrapponendo i due schemi potremo ricavare i valori delle forze agenti nei nodi

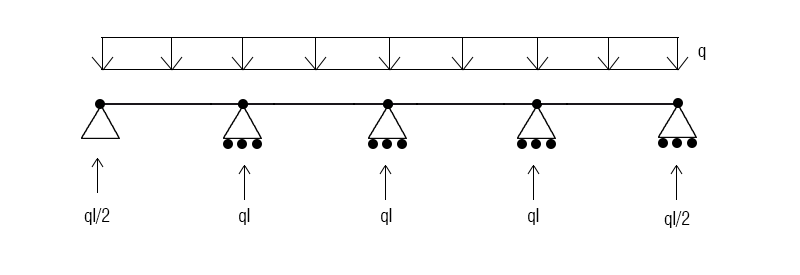
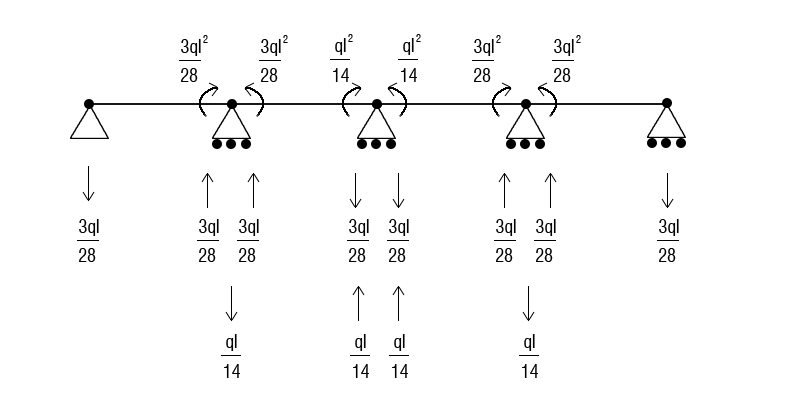
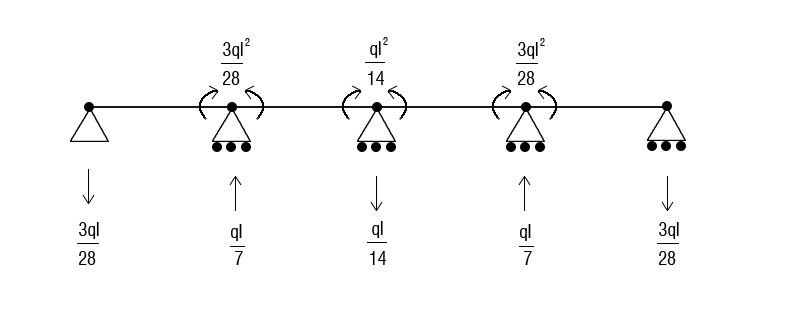
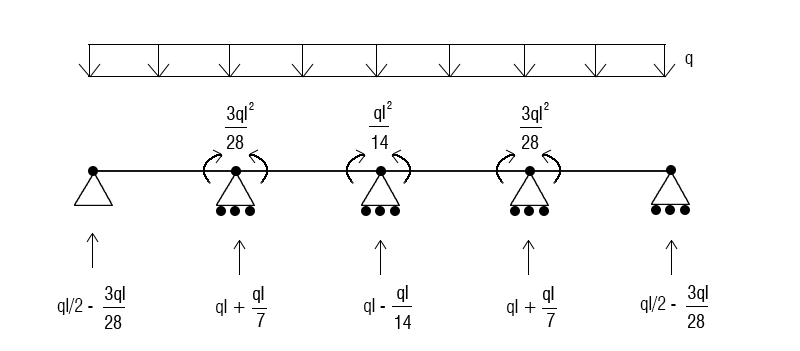
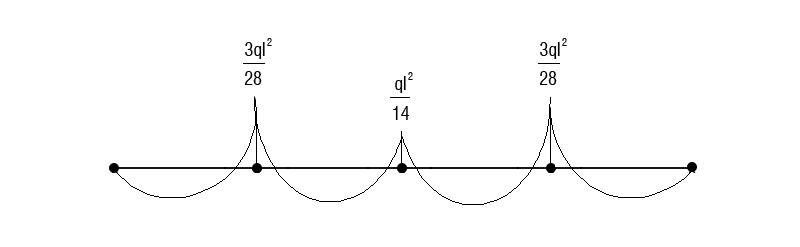
Conoscendo le forze agenti posso rappresentare il grafico del taglio e del momento