Esercitazione 4 -Metodo delle forze-

Esercitazione 4 -Metodo delle forze-

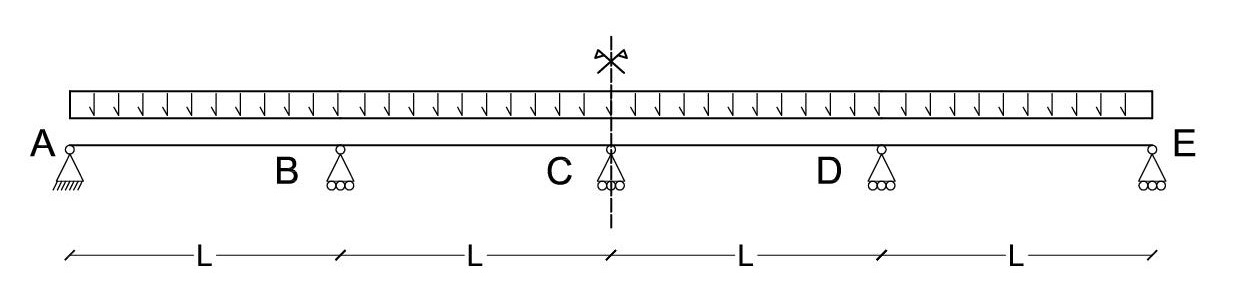
Trave tre volte iperstatica  NGL=3     NGV=6

La struttura è 3 volte iperstatica. Per risolvere la struttura con il metodo delle forze trasformo la struttura iniziale  in una struttura isostatica di riferimento. Trasformo le cerniere in B,C,D in cerniere interne applicando dei momenti X1,X2 in A e B, essendo la trave simmetrica nel punto C posso applicare X1. Si eliminano cosi i 3 gradi di vincoli.

Sistema equivalente isostatico

1.    Equazioni di compatibilità Cinematica

·       ΔφB=0       φBs – φBd=0

φBs= ql³/24EI – X1L/3EI

φBd= -ql³/24EI + X1L/3EI + X2L/6EI

·       ΔφC=0       φCs – φCd=0

φCs= ql³/24EI – X2L/3EI - X1L/6EI

φCd= -ql³/24EI + X2L/3EI + X1L/6EI

·       ΔφD=ΔφB

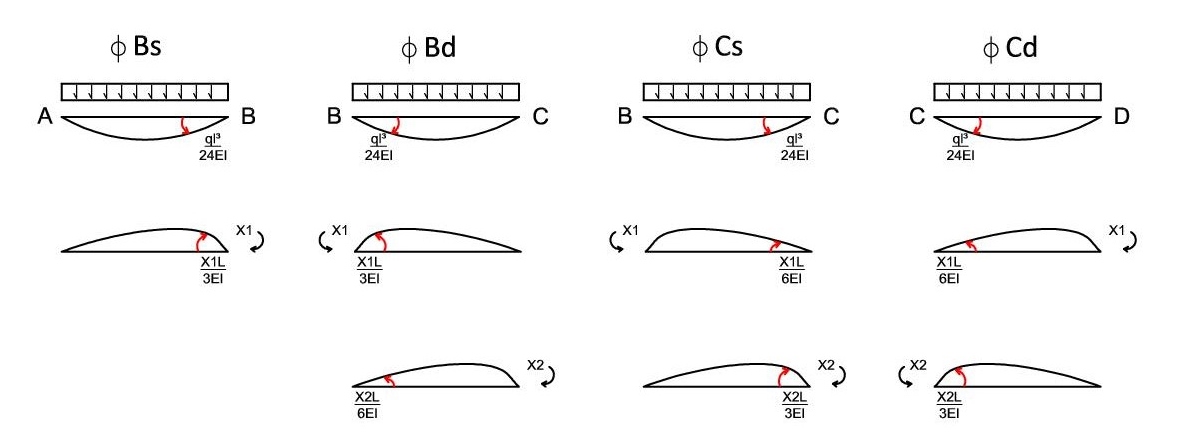
2.    Trovare X1 E X2

φBs – φBd=0

ql³/24EI - X1L/3EI+ ql³/24EI - X1L/3EI - X2L/6EI=0

2ql³/24EI - 2X1L/3EI - X2L/6EI=0

X2/2 = -2X1 + ql²/4

X2 = -4X1 + ql²/2          

φCs – φCd=0

ql³/24EI – X2L/3EI - X1L/6EI+ ql³/24EI - X2L/3EI - X1L/6EI=0

2ql³/24EI – 2X2L/3EI - 2X1L/6EI=0

-X1/2 = X2 - ql²/8          

X1 = - 2X2 - ql²/4          

X1=3/28 ql²

X2=1/14 ql²

2.    Reazioni

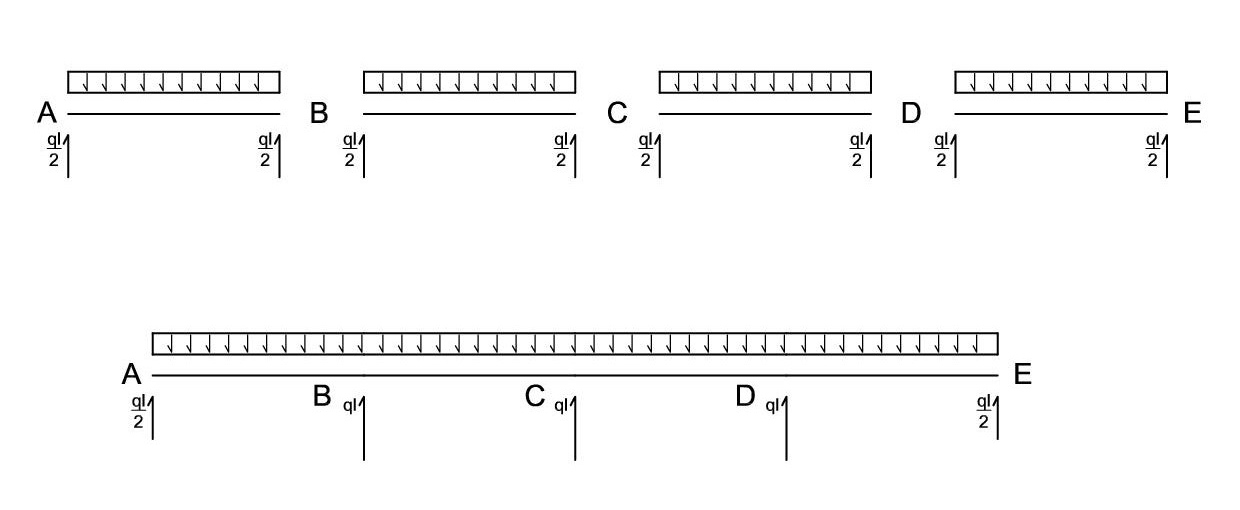
Reazioni dovute al carico

Reazioni dovute ai momenti  X1 e X2

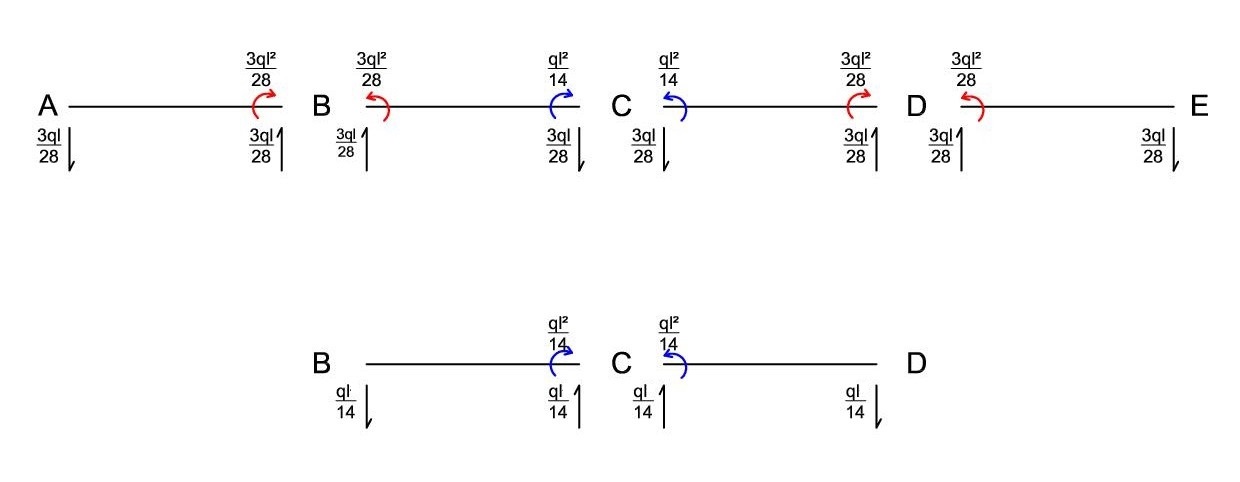
Somma delle reazioni dei momenti

Trovare le reazione finali dovute alla somma tra le reazione del carico  e dei momenti

Diagramma del taglio e del momento