blog di alessandro.mastrantoni

Trave Vierendeel

 

Il secondo esercizio sulla trave Vierendel è su doppio incastro ed è composta da 6 telaio shear type, sovrapposti e ruotati, in questo caso la struttura è simile al comportamento ad una trave doppiamente incastrata.

 

La struttura è simmetrica, quindi è necessario dividere la forza centrale in F/2.

Data la simmetria è sufficiente risolvere metà trave per poi ribaltare i risultati.

 

Trovare il taglio nei pilastri tramite l’equilibrio delle forze orizzontali tenendo conto che la forza viene assorbita dai 4 incastri e non più solo da due come l’esercizio precedente.

 

Diagramma taglio

 

È possibile trovare il momento e lo spostamento δdei traversi  tramite  

M= 6EI/l²*δ T= 12 EI/l³*δ  dove   δ= Tl³/12 EI

1.      T=F/4   M=Fl/8  δ=Fl³/48EI

2.      T=3F/4   M=3Fl/8  δ=3Fl³/48EI

3.      T=5F/4   M=5Fl/8  δ=5Fl³/48EI

 

Per determinare  Il momento dei traversi è possibile moltiplicare il taglio per il braccio che è pari ad  l/2.

Diagramma momento

 

Per trovare il momento sui montanti, bisogna scrivere l’equilibrio ai nodi.

 

Diagramma momento sui montanti

 

Per trovare i tagli è necessario sommare la coppia dei momenti agenti sul montante e dividendoli per la luce su cui lavorano (2L)

 

Taglio sui montanti

 

Deformata

 

 

 

 

Es. RIPARTIZIONE FORZA SISMICHE

 

Impalcato

L’impalcato di riferimento è interamente in cemento armato costituito da  12 pilastri che organizzano 8 telai, quattro lungo X e quattro lungo Y necessari a sopportare oltre il carico strutturale anche ad assorbire le sollecitazioni orizzontali dovuti al sisma.

 

I pilastri hanno un’altezza di 4 metri.

Sono presenti 4 molle nell’asse X e 4 nell’asse Y e indicano che, il solaio è pensato come rigido nel suo piano. 

• Step 1: calcolo delle rigidezze traslanti dei controventi dell'edificio

  Si inizia studiando singolarmente i 8 telai in base alla caratteristiche e l numero dei pilastri che li compongono

•  Step 2: tabella sinottica controventi e distanze

Tabella in cui vengono riportate le somme di rigidezza dei telai e le rispettive distanza dei pilastri dall’origine O.

 

• Step 3: calcolo del centro di massa

Per il calcolo del centro di massa dell’intero impalcato è necessario determinare l’area dei singoli rettangoli (area 1,area2,area3) e le distanze dei rispettivi centri di massa.

 

• Step 4: calcolo del centro di rigidezze e delle rigidezze globali

Si calcola in centro di rigidezza  che è il punto in cui è applicata la risultante delle forze resistenti.

 

• Step 5: analisi dei carichi sismici 

• Step 6: ripartizione forza sismica lungo X

 

• Traslazione dell’impalcato lungo l’asse x

• Step 7: ripartizione forza sismica lungo Y

 

•  Traslazione dell’impalcato lungo l’asse y

• Centro di massa e centro di rigidezza

Es5 -Trave Vierendeel-

La trave Vierendeelha lo stesso comportamento di un telaio “shear-type” solo che è ruotato di 90 gradi. La trave è infinitamente resistente a flessione, mentre i pilastri  per effetto delle forze esterne traslano di una quantità δ ma senza deformarsi. 

 

Per risolvere la trave occorre risolvere ogni tratto verticale considerandolo come se fosse una trave doppiamente appoggiata.

Trave iperstatica  soggetta ad un cedimento vincolare δ,  si hanno i seguenti valori notevoli del momento e del taglio.

M= 6EI/l²*δ     T= 12 EI/l³*δ

 

Si trovano i valore di ogni asta orizzontale

 1.      F = 2T  → F = 24 EI/l³δ1  

         δ1= Fl³/24 EI

 T = 12 EI/l³*δ1  

M = 6 EI/l²*δ1

T = 12 EI/l³*(Fl³/24 EI) = F/2

M = 6 EI/l²*(Fl³/24 EI)  = Fl/4

 

2.      F + F/2 + F/2= 2T  → 2F = 24 EI/l³*δ2   

        δ2= Fl³/12 EI

T = 12 EI/l³*δ2

M = 6 EI/l²*δ2

T = 12 EI/l³*(Fl³/12 EI) = F

M = 6 EI/l²*(Fl³/12 EI)  = Fl/2

 

3.      F + F + F= 2T  → 3F = 24 EI/l³*δ3 

         δ3= Fl³/8 EI

T = 12 EI/l³*δ3

M = 6 EI/l²*δ3

T =12 EI/l³*(Fl³/8 EI) = 3/2F

M =6 EI/l²*(Fl³/8 EI) = 3/4 Fl

 

4.      F + 3/2F + 3/2F= 2T  → 4F = 24 EI/l³*δ4 

         δ4= Fl³/6 EI

T = 12 EI/l³ δ3

M = 6 EI/l²*δ4

T = 12 EI/l³ * (Fl³/6 EI) = 2F

M = 6 EI/l²*(Fl³/6 EI)=  Fl

 

5.      F + 2F + 2F= 2T  → 5F = 24 EI/l³*δ5  

        δ5= 5 Fl³/ 24EI

T = 12 EI/l³*δ2

M = 6 EI/l²*δ2

T = 12 EI/l³*(5 Fl³/24 EI) = 5/2F

M = 6 EI/l²*(5 Fl³/24 EI) = 5/4Fl

 

6.      F + 5/2F + 5/2F= 2T  → 6F = 24 EI/l³*δ6   

         δ1= Fl³/4 EI

T = 12 EI/l³*δ1

M = 6 EI/l²*δ6

T = 12 EI/l³*(Fl³/4 EI) = 3F

M = 6 EI/l²*(Fl³/4 EI)=3/2 Fl

• Distribuzione delle forze orizzontale

• Diagramma del Taglio dei traversi

 

 

 

 

• Diagramma del Momento dei traversi

• Ora si deve trovare i momenti degli elementi verticali, per trovarli basta fare l’equilibrio di ogni nodo

1

 

2

 

3

FL/2 + FL/4 =5/4 FL

4

3FL/4 + FL =7/4 FL

5

FL + 5Fl/4 =9/4 FL

6

5FL/4 + 3Fl/2 =11/4 FL

 

Posso trovare i valori dei tagli, calcolando l'equilibrio di ciascuna asta verticale:

1

2

3

 

(5FL/4+5FL/4) /2L= 5FL

 

4

(7FL/4+7FL/4) /2L=7FL

 

5

(9FL74+9FL/4) /2L=9FL

 

6

(11FL/4+11FL/4) /2L=11FL

 

• Diagramma taglio ritti

 

• Diagramma momento ritti

 

 

 

Si può facilmente determinare lo sforzo normale sui traversi, poiché è pari al taglio dei ritti che si trasmettono ai traversi e diventano sforzo normale.

 

 

Verifica con sap dove si deve cambiare il Modulo Elastico per rendere la struttura infinitivamente rigida.

Deformata

 

Diagramma del taglio

 

Diagramma del momento

 

 

 

Esercitazione 4 -Metodo delle forze-

 

Trave tre volte iperstatica  NGL=3     NGV=6

La struttura è 3 volte iperstatica. Per risolvere la struttura con il metodo delle forze trasformo la struttura iniziale  in una struttura isostatica di riferimento. Trasformo le cerniere in B,C,D in cerniere interne applicando dei momenti X1,X2 in A e B, essendo la trave simmetrica nel punto C posso applicare X1. Si eliminano cosi i 3 gradi di vincoli.

 

Sistema equivalente isostatico

 

1.    Equazioni di compatibilità Cinematica

·       ΔφB=0       φBs – φBd=0

φBs= ql³/24EI – X1L/3EI

φBd= -ql³/24EI + X1L/3EI + X2L/6EI

 

·       ΔφC=0       φCs – φCd=0

φCs= ql³/24EI – X2L/3EI - X1L/6EI

φCd= -ql³/24EI + X2L/3EI + X1L/6EI

 

·       ΔφD=ΔφB

 

 

 

 

2.    Trovare X1 E X2

φBs – φBd=0

ql³/24EI - X1L/3EI+ ql³/24EI - X1L/3EI - X2L/6EI=0

2ql³/24EI - 2X1L/3EI - X2L/6EI=0

X2/2 = -2X1 + ql²/4

X2 = -4X1 + ql²/2          

 

φCs – φCd=0

ql³/24EI – X2L/3EI - X1L/6EI+ ql³/24EI - X2L/3EI - X1L/6EI=0

2ql³/24EI – 2X2L/3EI - 2X1L/6EI=0

-X1/2 = X2 - ql²/8          

X1 = - 2X2 - ql²/4          

X1=3/28 ql²

X2=1/14 ql²

 

2.    Reazioni

Reazioni dovute al carico

 

Reazioni dovute ai momenti  X1 e X2

 

Somma delle reazioni dei momenti

 

Trovare le reazione finali dovute alla somma tra le reazione del carico  e dei momenti

Diagramma del taglio e del momento

 

 

 

 

Dimensionamento Trave in un solaio in Legno

1.       Disegnare il solaio:

Dimensionare il solaio con interasse trave 3 m

Scegliere l’orditura del solaio

 

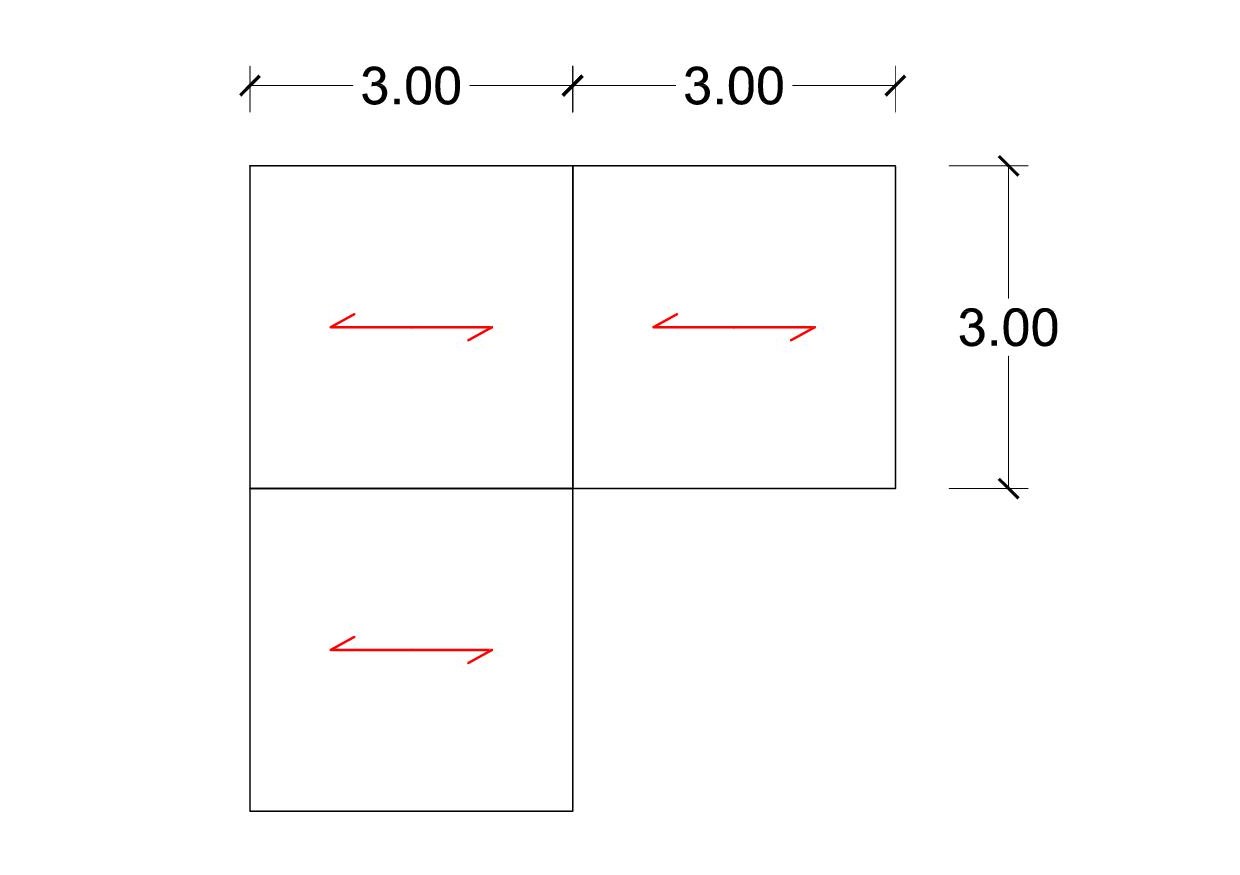
2.       Trovare la trave più sollecitata e la rispettiva area di influenza dei carichi

 

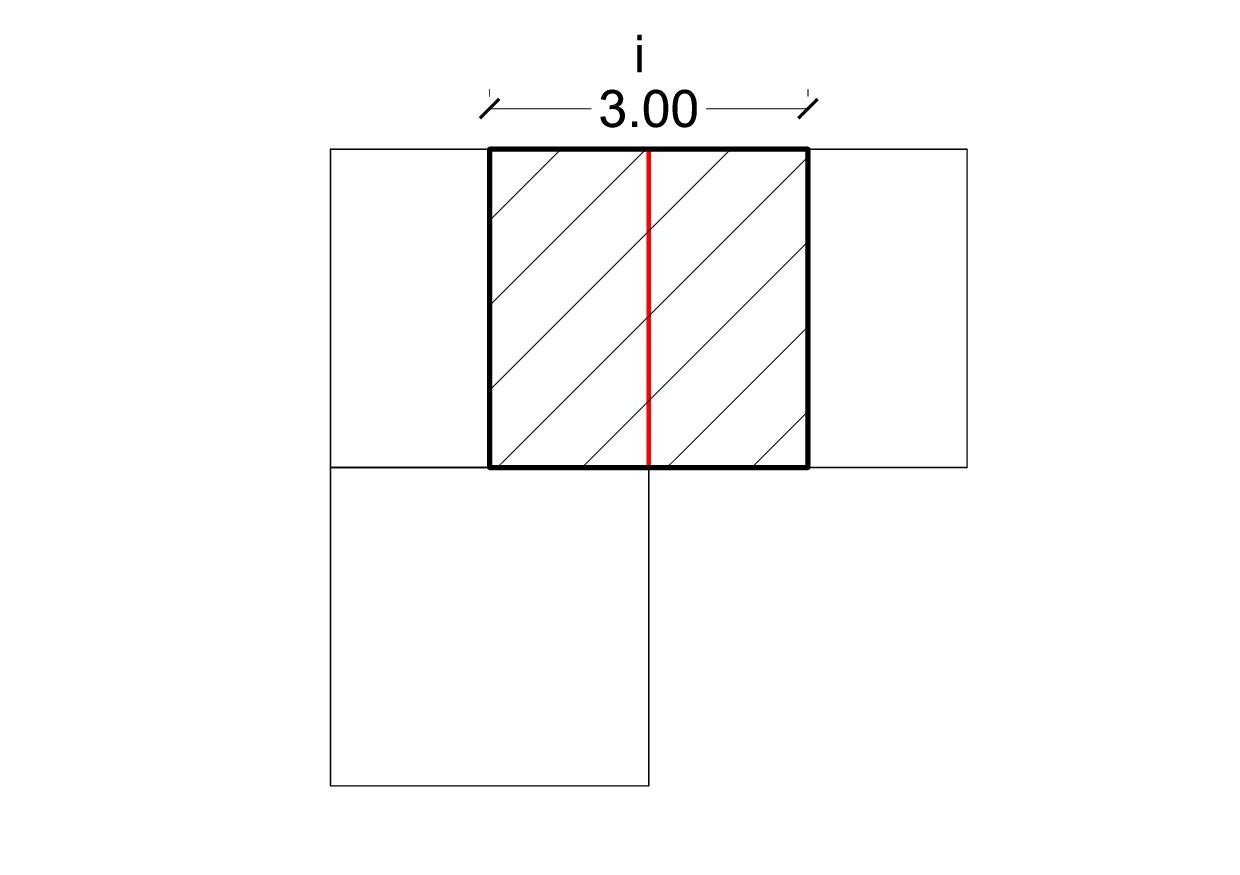
3.       Solaio in legno sistema a secco con riscaldamento (porzione di 1m)

 

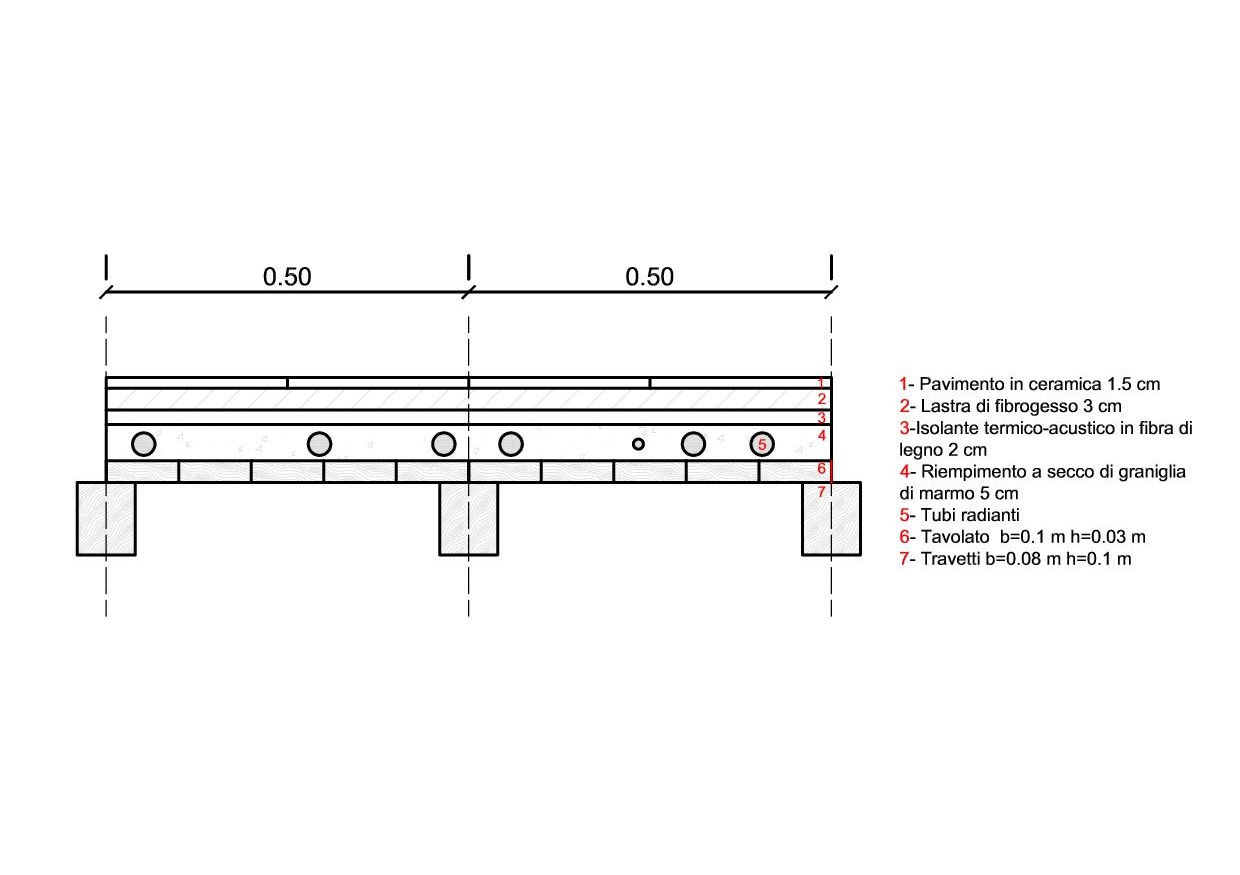
Calcolare i pesi agenti sulla trave

4.       qs Peso di 1mq di solaio Lamellare conifero

·         Peso di 2 Travetti  (b=0.08m  h=0.1m)    γ = 6 kn/mc   V=0.008mc  P=γ *V

                                  P1=0.048 kn/mq*2=0.096 kn/mq

·         Peso di 20 Tavole (b=0.1m  h=0.03m)    γ = 6 kn/mc   V=0.003mc  P=γ *V

                                 P2=0.018 kn/mq*20=0.36 kn/mq

Qs=P1+P2=0.456 kn/mq

5.       qp Sovraccarico permanente di 1 mq

·         Sottofondo di riempimento a secco con graniglia di marmo γ = 1.4 kn/mc  P=γ *Spessore

          P3= 1.4 kn/mc * 0.05 m= 0.07kn/mq

·         Isolante termico-acustico in fibra di legno  γ = 0.5 kn/mc  P=γ *Spessore

         P4= 0.5 kn/mc * 0.02 m= 0.01kn/mq

·         Lastra di fibrogesso   γ = 0.35 kn/mc  P=γ *Spessore

         P5= 0.35 kn/mc * 0.03 m= 0.01kn/mq

·         Pavimento in ceramica  γ = 20 kn/mc  P=γ *Spessore

         P6= 20 kn/mc * 0.015 m= 0.3 kn/mq

·         Avendo il riscaldamento a pavimento il peso degli impianti è maggiore di 0.5 kn/mq e diventa             P7= 0.8 kn/mq

·         Tramezzi P8=1 kn/mq

QP=P3+P4+P5+P6+P7+P8=2.19 kn/mq

6.     Qd Carico accidentale

·         Ambienti ad uso residenziali  P9=2 kn/mq

Qd= 2 kn/mq

7.       Una volta trovati i carichi agenti nella trave più sollecitata si inseriscono i dati sul foglio Excel

i=6 metri

qs=0.456 kn/mq           qp=2.19 kn/mq          qd= 2 kn/mq

q= somma de carichi*i

luce=lunghezza trave

M=momento pari a ql²/8

Fm,k= resistenza a flessione del legno lamellare  classe GL 24c pari a 24 N/mm²

Kmod=coefficiente correttivo che tiene conto dell’effetto della durata del carico sia dell’umiduta della struttura                      poichè ho scelto un legno lamellare incollato EN 14080 classe 2 il Kmod permanente è 0.6

γ_amm= sigma ammissibile 

b=la base della trave la dimensioniamo noi, io ho impostato b=18 cm

 

Dai calcoli effettuati la dimensione della trave viene  b=18cm   h=22.93cm ma poiché la dimensione delle travi lamellari sono multiplo di 4 cm la trave ultima è di  b=18cm   h=24 cm