Es5 -Trave Vierendeel-

Es5 -Trave Vierendeel-

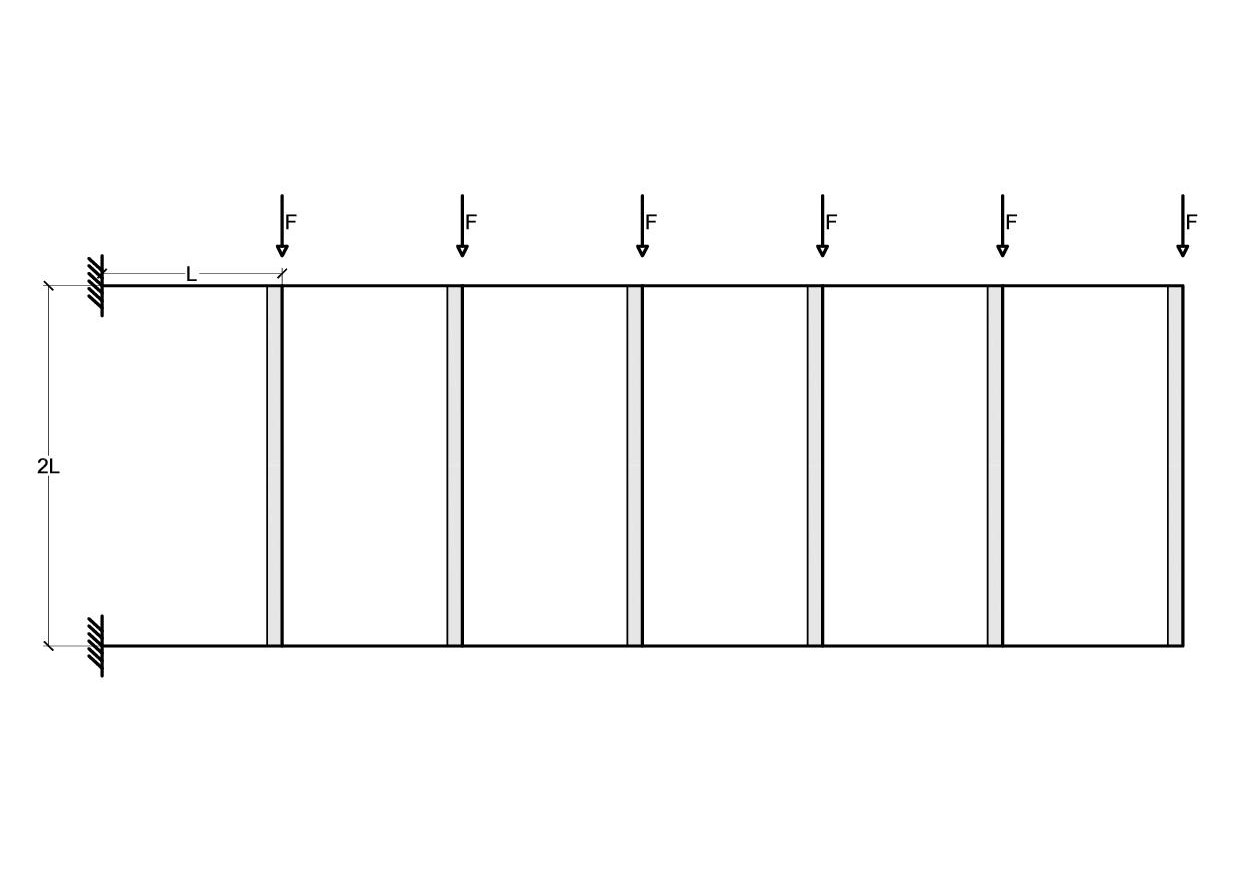La trave Vierendeelha lo stesso comportamento di un telaio “shear-type” solo che è ruotato di 90 gradi. La trave è infinitamente resistente a flessione, mentre i pilastri  per effetto delle forze esterne traslano di una quantità δ ma senza deformarsi. 

 

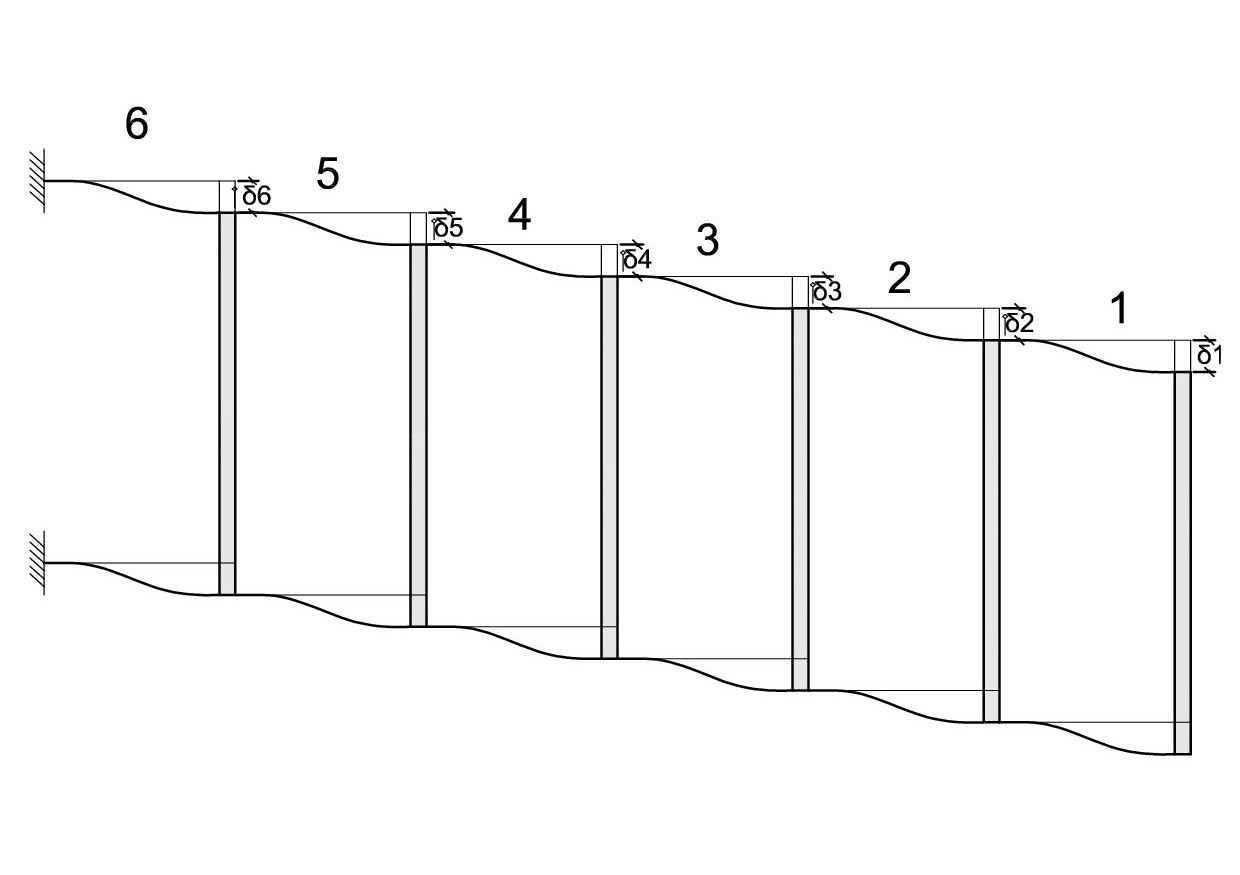
Per risolvere la trave occorre risolvere ogni tratto verticale considerandolo come se fosse una trave doppiamente appoggiata.

Trave iperstatica  soggetta ad un cedimento vincolare δ,  si hanno i seguenti valori notevoli del momento e del taglio.

M= 6EI/l²*δ     T= 12 EI/l³*δ

 

Si trovano i valore di ogni asta orizzontale

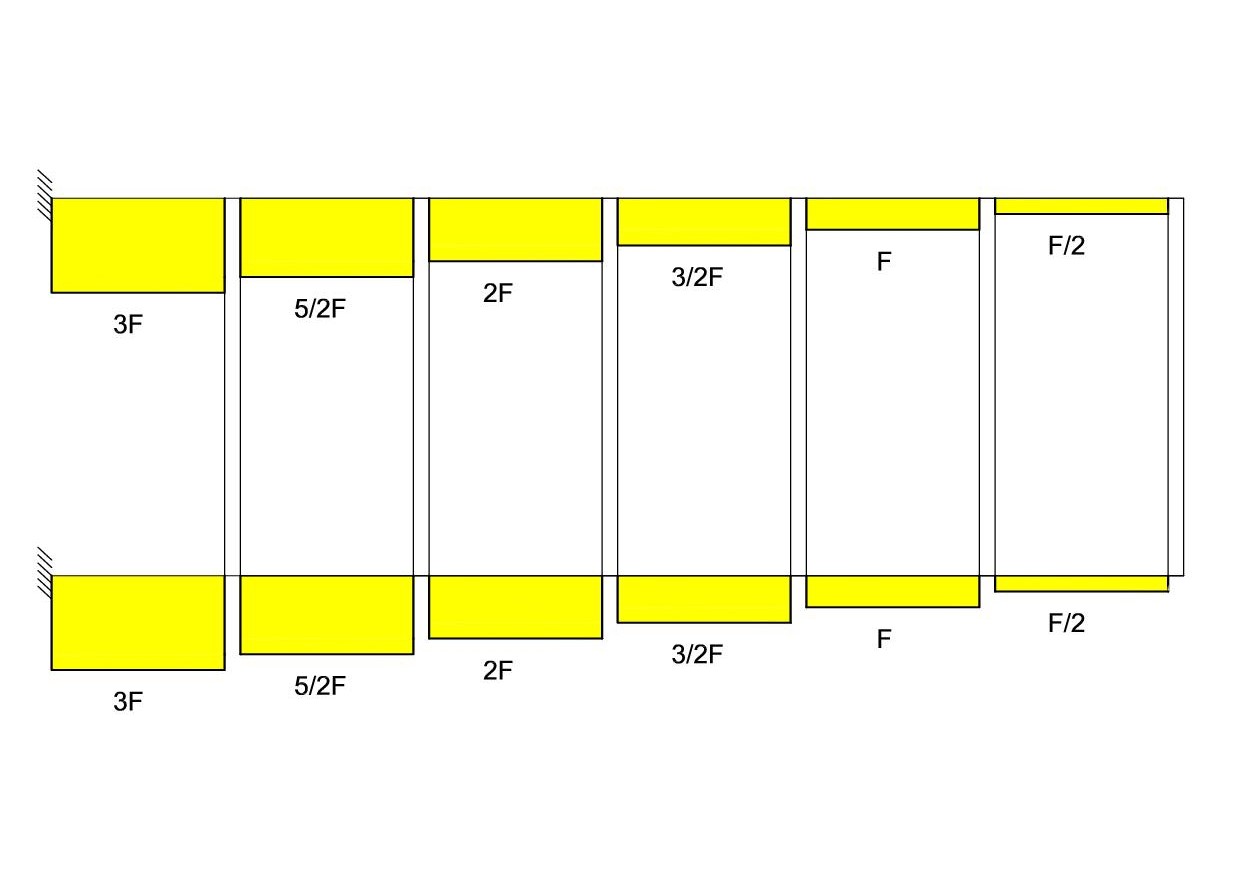
 1.      F = 2T  → F = 24 EI/l³δ1  

         δ1= Fl³/24 EI

 T = 12 EI/l³*δ1  

M = 6 EI/l²*δ1

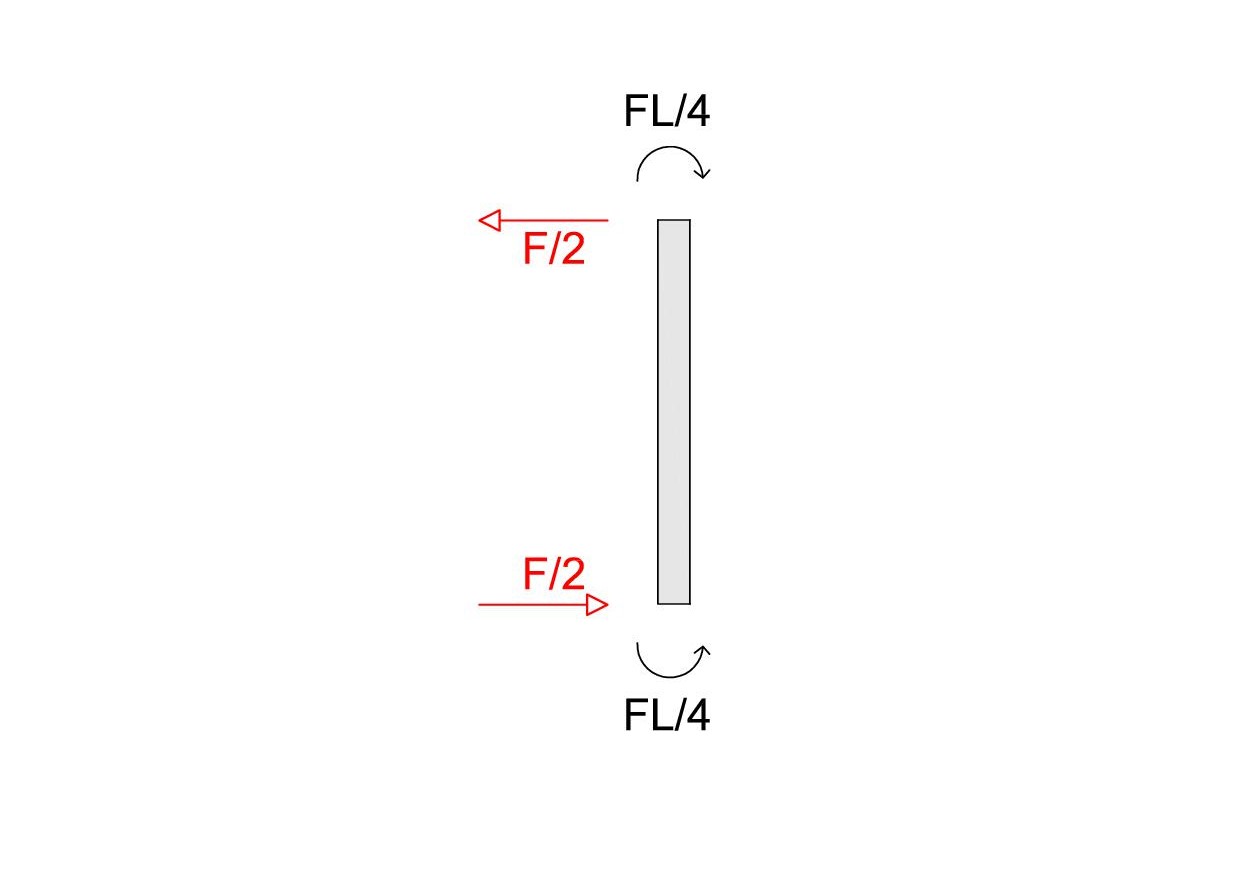
T = 12 EI/l³*(Fl³/24 EI) = F/2

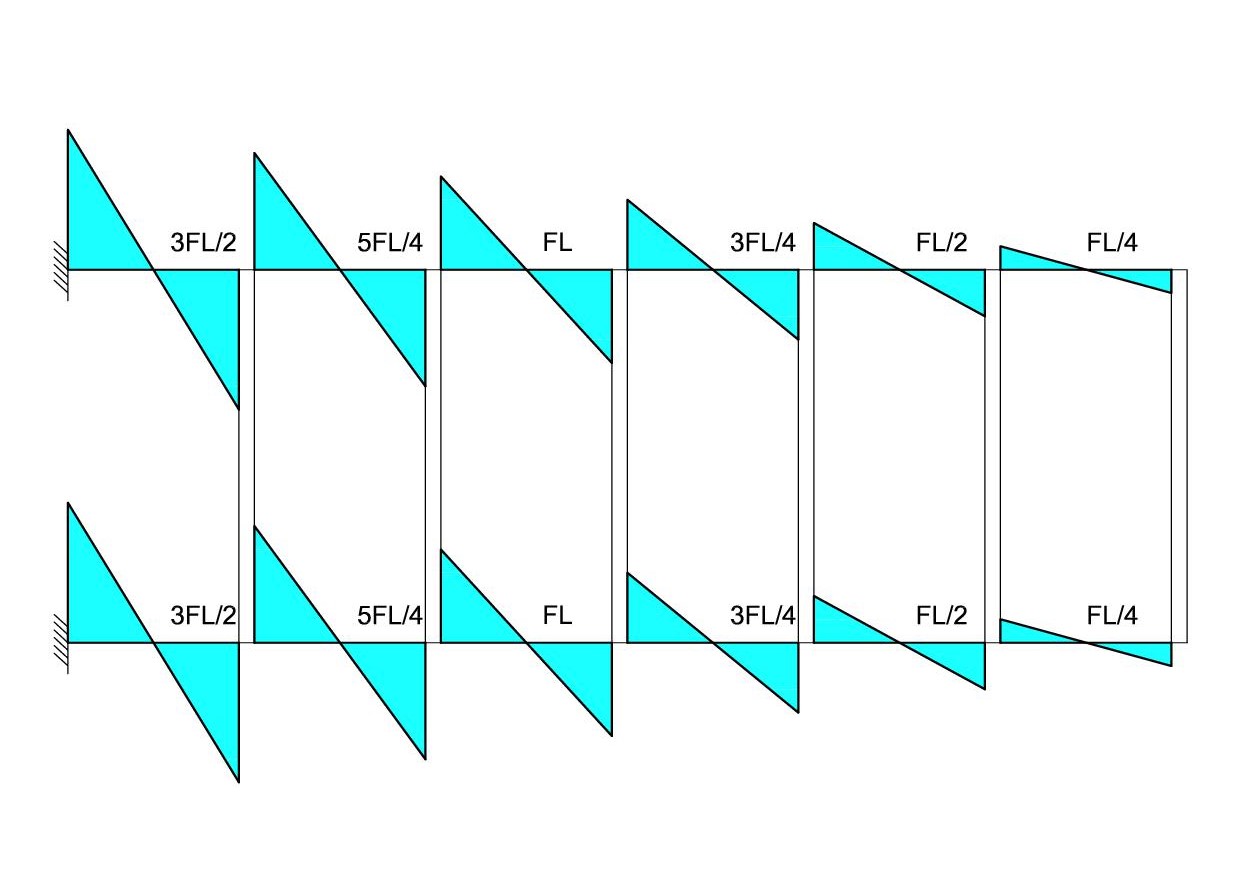
M = 6 EI/l²*(Fl³/24 EI)  = Fl/4

 

2.      F + F/2 + F/2= 2T  → 2F = 24 EI/l³*δ2   

        δ2= Fl³/12 EI

T = 12 EI/l³*δ2

M = 6 EI/l²*δ2

T = 12 EI/l³*(Fl³/12 EI) = F

M = 6 EI/l²*(Fl³/12 EI)  = Fl/2

 

3.      F + F + F= 2T  → 3F = 24 EI/l³*δ3 

         δ3= Fl³/8 EI

T = 12 EI/l³*δ3

M = 6 EI/l²*δ3

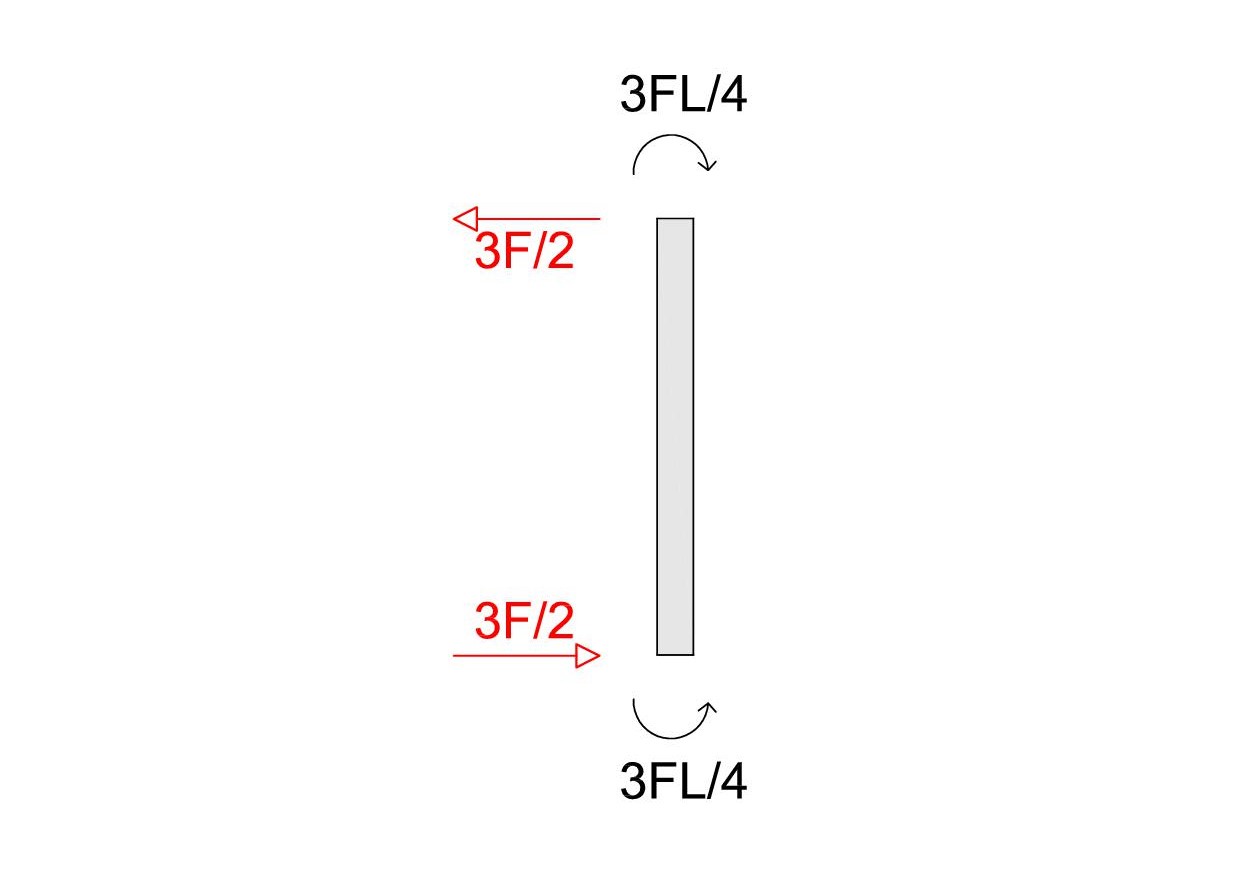
T =12 EI/l³*(Fl³/8 EI) = 3/2F

M =6 EI/l²*(Fl³/8 EI) = 3/4 Fl

 

4.      F + 3/2F + 3/2F= 2T  → 4F = 24 EI/l³*δ4 

         δ4= Fl³/6 EI

T = 12 EI/l³ δ3

M = 6 EI/l²*δ4

T = 12 EI/l³ * (Fl³/6 EI) = 2F

M = 6 EI/l²*(Fl³/6 EI)=  Fl

 

5.      F + 2F + 2F= 2T  → 5F = 24 EI/l³*δ5  

        δ5= 5 Fl³/ 24EI

T = 12 EI/l³*δ2

M = 6 EI/l²*δ2

T = 12 EI/l³*(5 Fl³/24 EI) = 5/2F

M = 6 EI/l²*(5 Fl³/24 EI) = 5/4Fl

 

6.      F + 5/2F + 5/2F= 2T  → 6F = 24 EI/l³*δ6   

         δ1= Fl³/4 EI

T = 12 EI/l³*δ1

M = 6 EI/l²*δ6

T = 12 EI/l³*(Fl³/4 EI) = 3F

M = 6 EI/l²*(Fl³/4 EI)=3/2 Fl

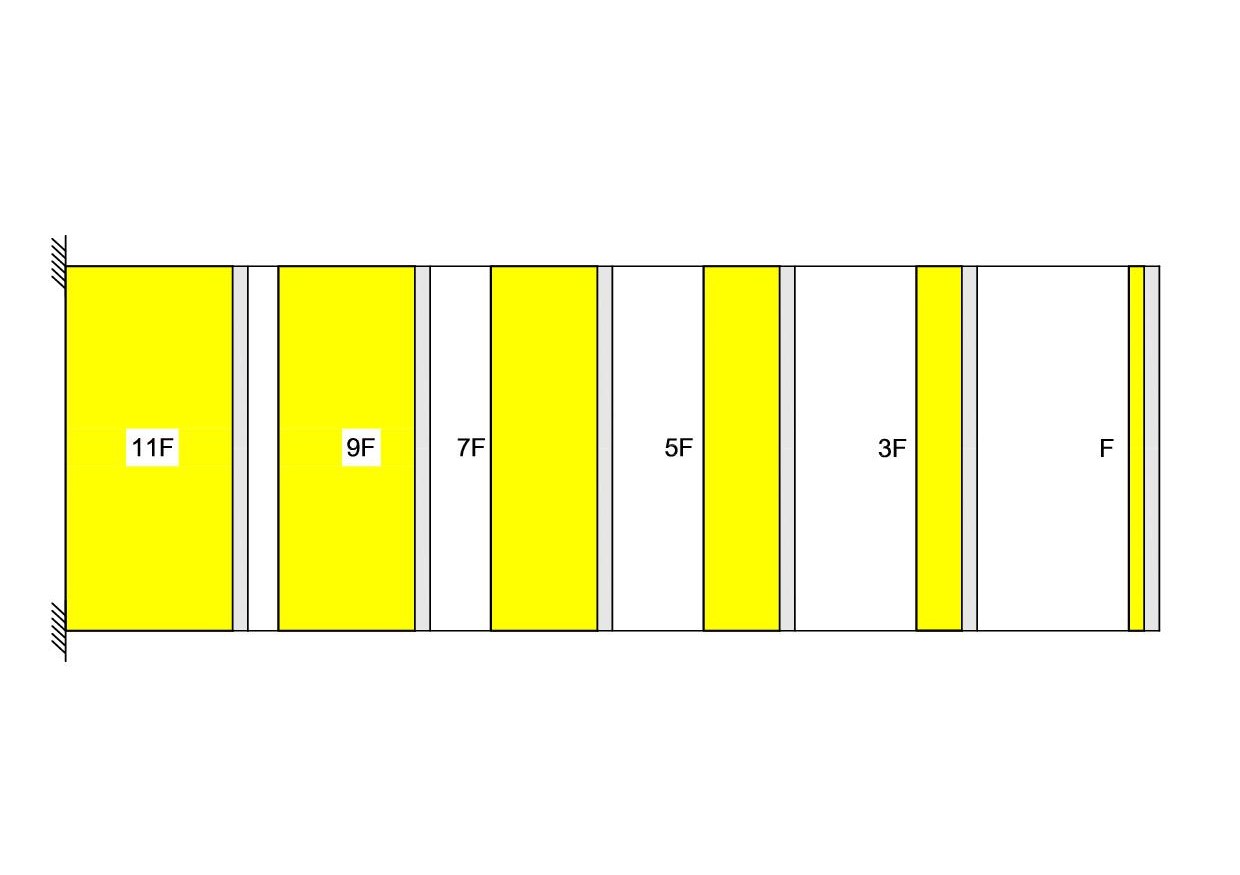
• Distribuzione delle forze orizzontale

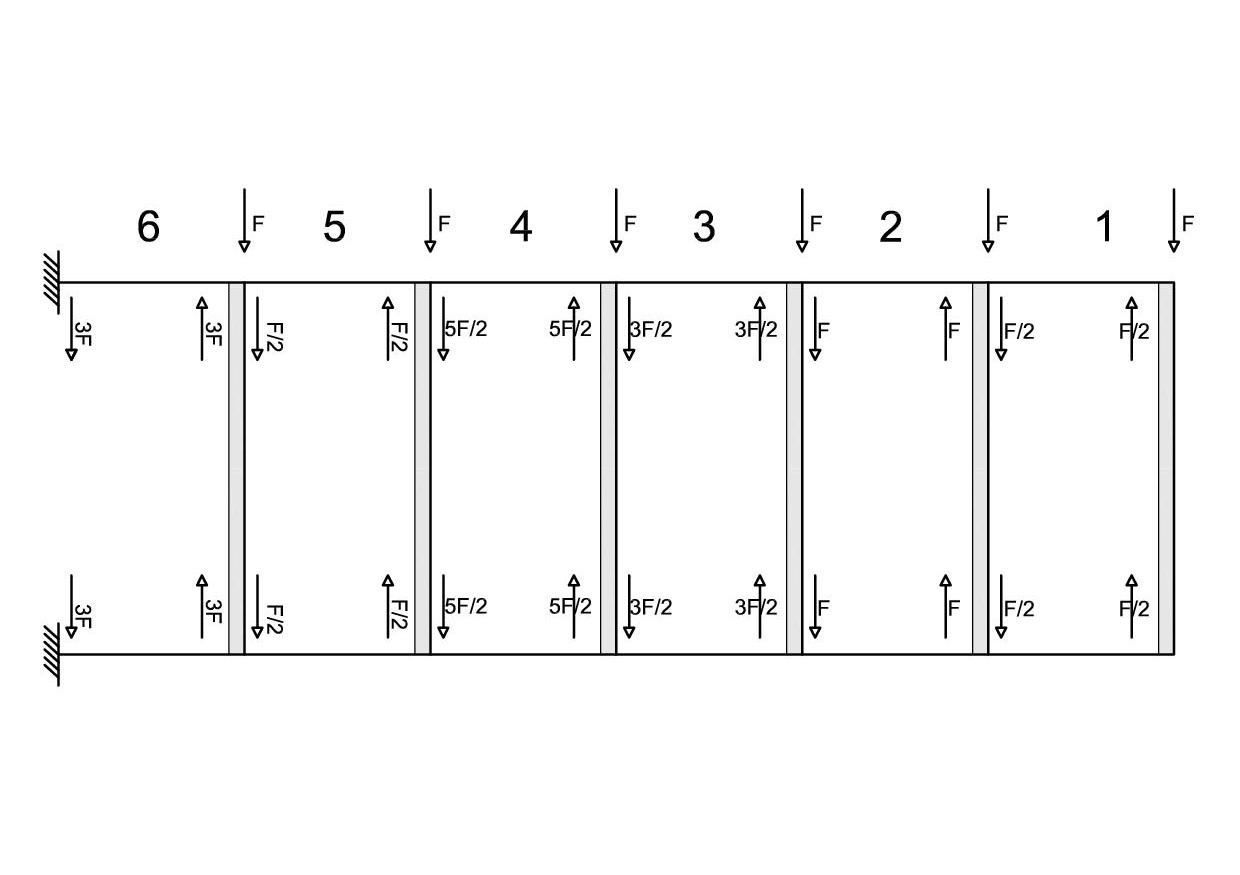
• Diagramma del Taglio dei traversi

 

 

 

 

• Diagramma del Momento dei traversi

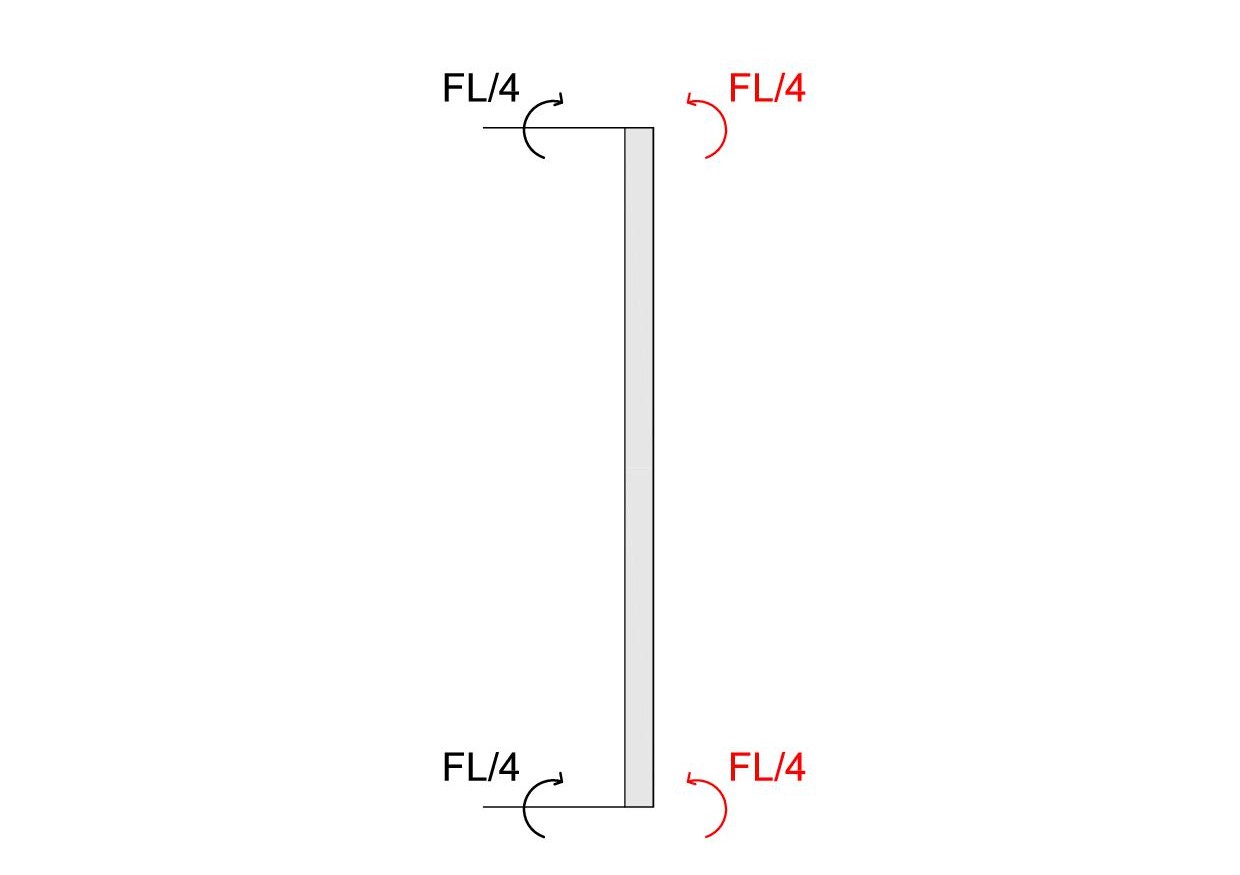
• Ora si deve trovare i momenti degli elementi verticali, per trovarli basta fare l’equilibrio di ogni nodo

1

 

2

 

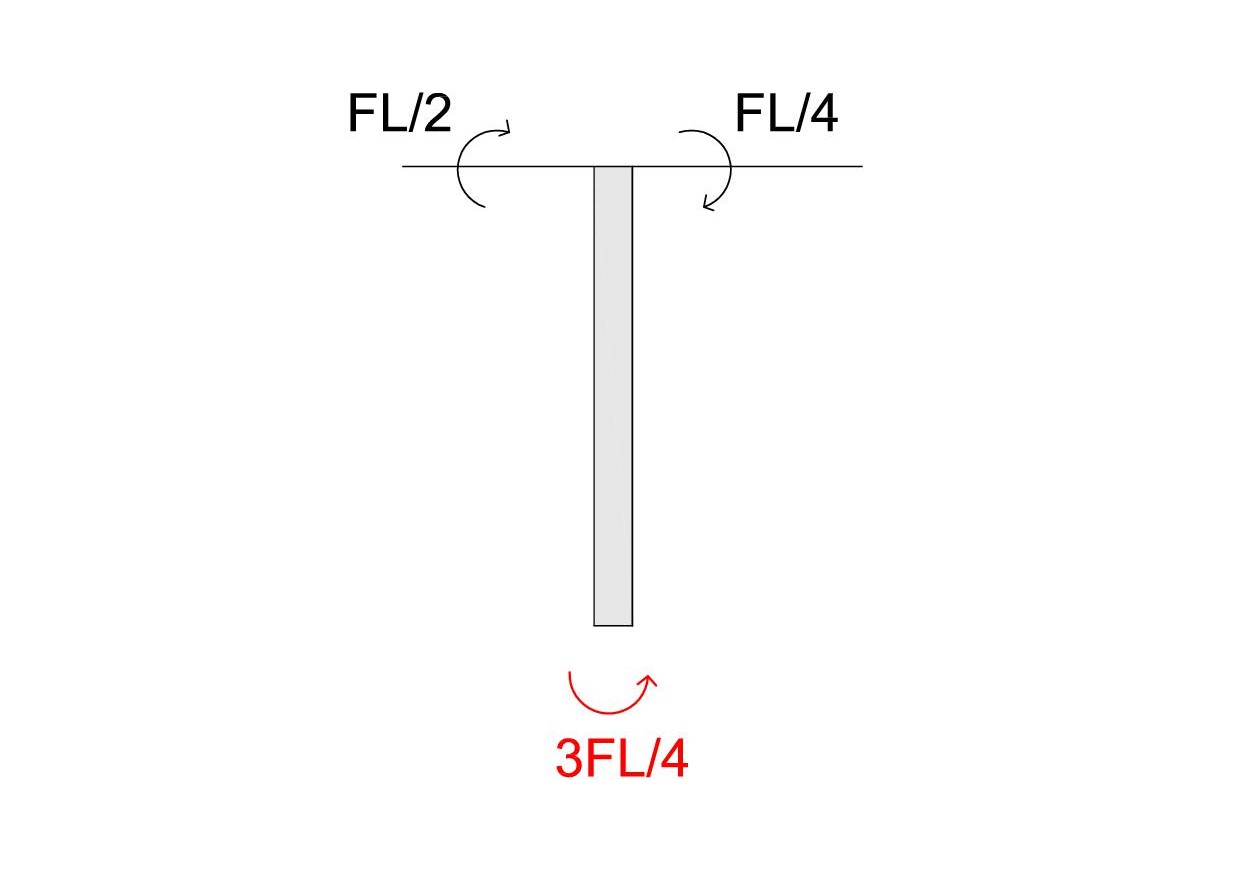
3

FL/2 + FL/4 =5/4 FL

4

3FL/4 + FL =7/4 FL

5

FL + 5Fl/4 =9/4 FL

6

5FL/4 + 3Fl/2 =11/4 FL

 

Posso trovare i valori dei tagli, calcolando l'equilibrio di ciascuna asta verticale:

1

2

3

 

(5FL/4+5FL/4) /2L= 5FL

 

4

(7FL/4+7FL/4) /2L=7FL

 

5

(9FL74+9FL/4) /2L=9FL

 

6

(11FL/4+11FL/4) /2L=11FL

 

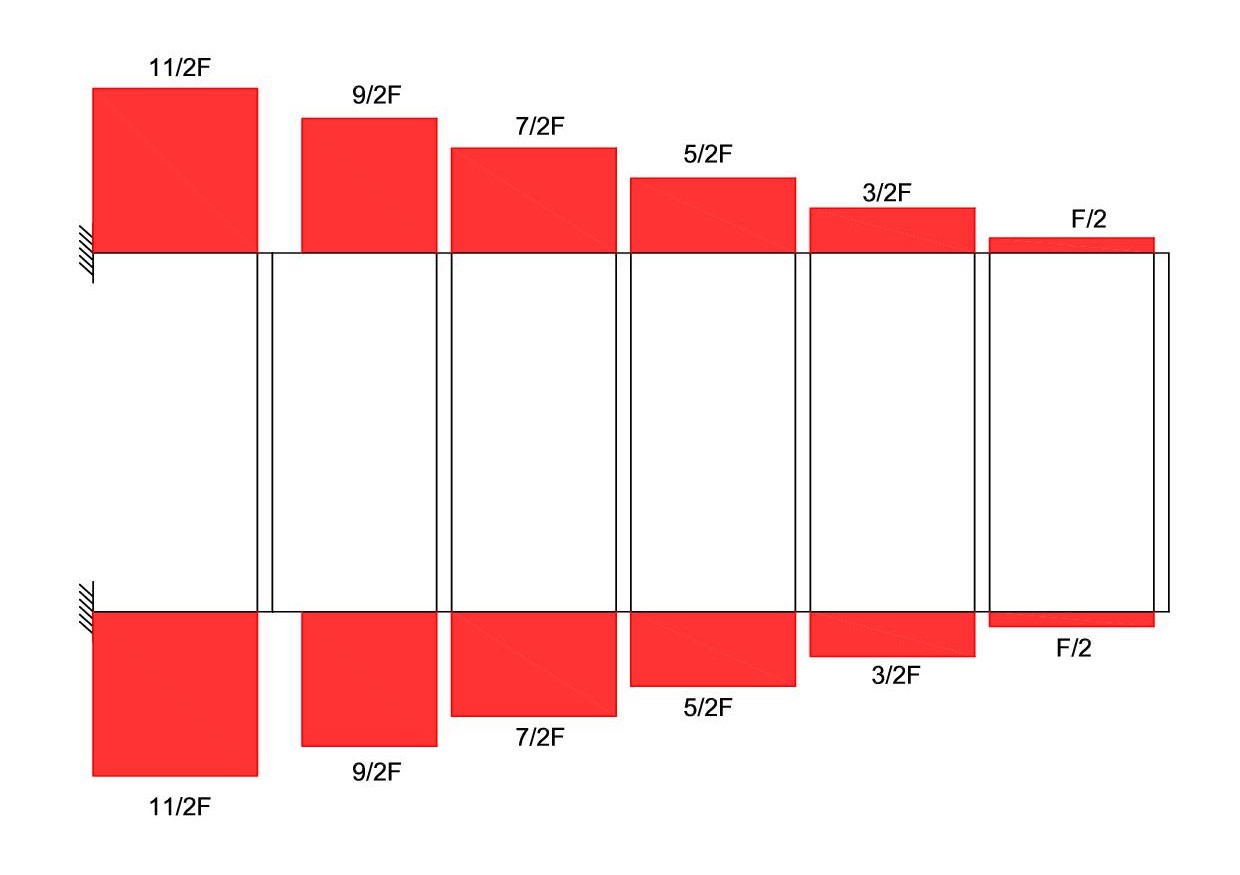
• Diagramma taglio ritti

 

• Diagramma momento ritti

 

 

 

Si può facilmente determinare lo sforzo normale sui traversi, poiché è pari al taglio dei ritti che si trasmettono ai traversi e diventano sforzo normale.

 

 

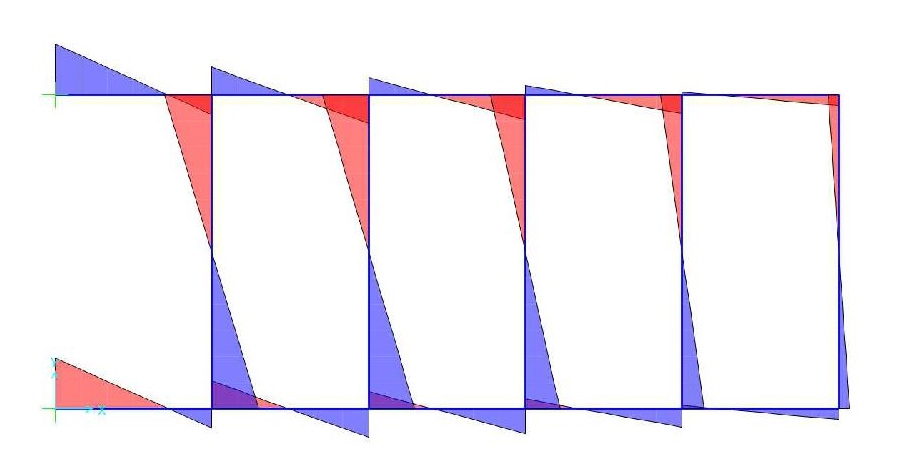
Verifica con sap dove si deve cambiare il Modulo Elastico per rendere la struttura infinitivamente rigida.

Deformata

 

Diagramma del taglio

 

Diagramma del momento