Esercitazione 4 - Risoluzione di un sistema iperstatico mediante il metodo delle forze

RISOLUZIONE DI UN SISTEMA IPERSTATICO MEDIANTE IL METODO DELLE FORZE

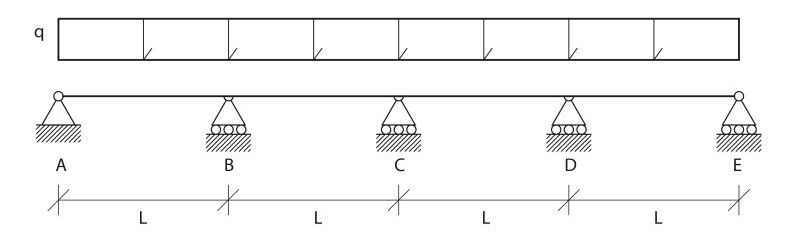
Per la risoluzione dello schema statico qui rappresentato verrà applicato il metodo delle forze, che prevede di declassare vincoli fino a raggiungere l'isostaticità e sostituendoli con forze incognite, che corrispondono alle reazione che i vincoli appena esclusi fornirebbero come risposta ai carichi agenti.

La scelta dei vincoli da declassare è dettata dalla conoscenza del valore di abbassamenti e rotazioni nelle condizioni di carico e schema strutturale che si presenta. In questo caso trasformare le cerniere esterne in cerniere interne aggiungendo dei momenti agenti a destra e a sinistra risolve il problema agevolmente: i momenti infatti ripristinano la condizione di vincolo esclusa, garantendo la simmetria delle rotazioni a destra e a sinistra della cerniera interna appena inserita. Inoltre è noto il valore della rotazione in quell'ambito. Al contrario, declassando la reazione verticale dei carrelli e sostituendola con delle forze verticali, per risolvere il problema sarebbe stato necessario conoscere gli abbassamenti della trave non solo in mezzeria, ma anche a ¼L (valore valido anche a ¾ della lunghezza per simmetria di condizioni di carico e vincolo). Per arrivare a queste informazioni sarebbe stato necessario applicare il metodo della linea elastica, grazie al quale sono note le informazioni riguardo i valori delle rotazioni e abbassamenti nelle condizioni che si presentano in questo caso. Nel caso del momento applicato all'estremo è importante considerare che non imprime solo una rotazione nel punto in cui è applicato, ma anche una rotazione di entità dimezzata all'altro estremo.

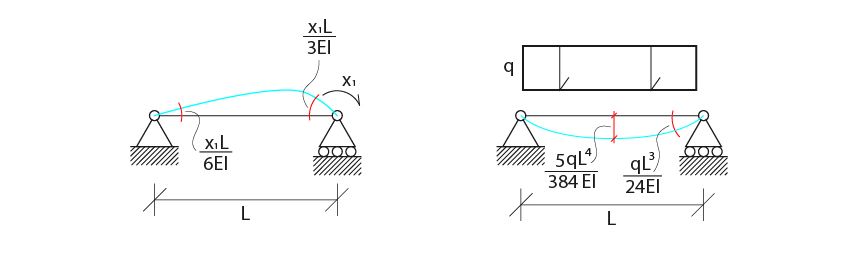
Questo è lo schema alternativo, risultato dell'applicazione del metodo delle forze.

I momenti aggiunti in seguito al declassamento dei vincoli sono ovviamente incogniti. Per trovarne il valore bisogna eguagliare le rotazioni a destra e a sinistra della cerniera, eguaglianza che questi stessi momenti assicurano. Sempre grazie alla simmetria delle condizioni di carico e di vincolo è possibile considerare X₁ = X₃.

Per trovare il valore di X₁ ed X₂ è sufficiente mettere a sistema 2 equazioni ottenute eguagliando le rotazioni a destra e a sinistra dei punti B e C.

trovato il valore dei momenti è possibile calcolare le reazioni vincolari dei 2 sistemi, quello con i momenti e quello con il carico ripartito, considerando la trave sempre come discontinua.

La somma delle reazioni, per il principio di sovrapposizione degli effetti, darà come risultato quelle della struttura obbiettivo dell'esercizio.

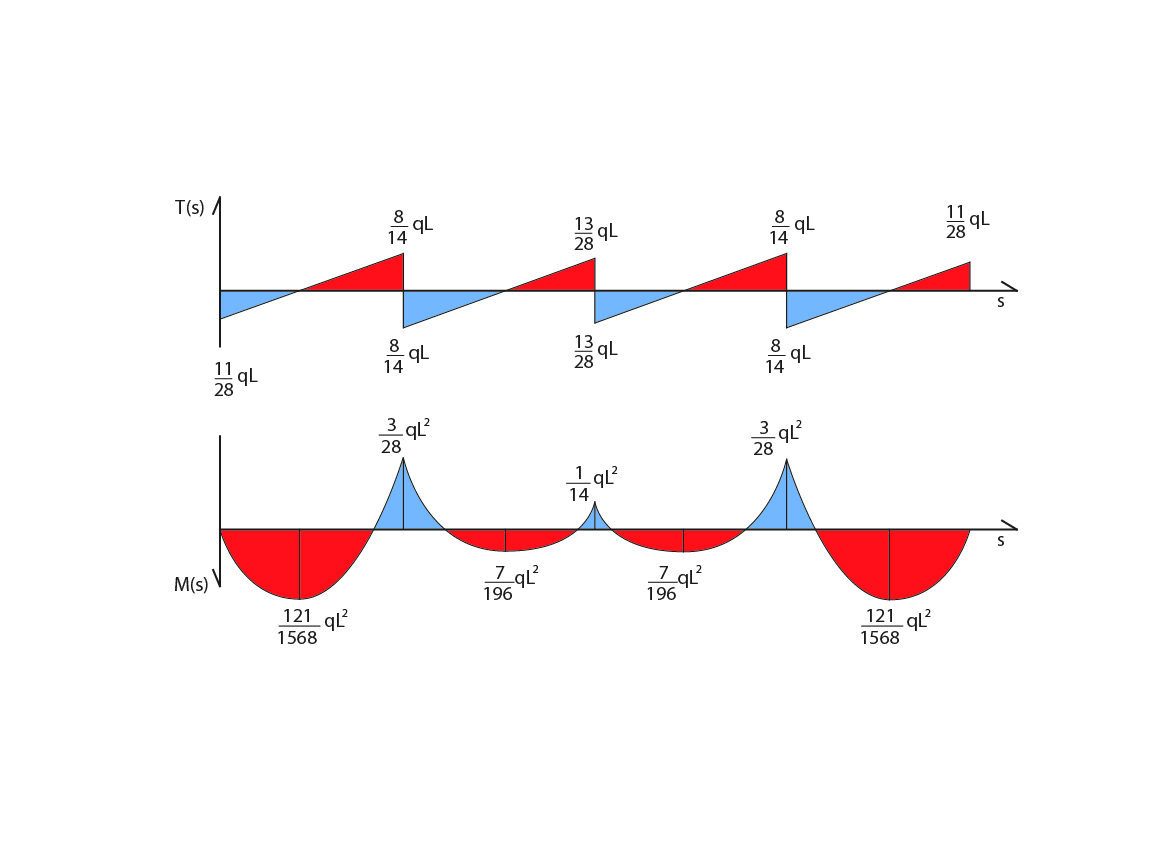
Ora è possibile disegnare i grafici del Taglio e del Momento flettente lungo la trave.