Esercitazione V_Trave Vierendeel

Inviato da dario.taffi il Sab, 27/04/2013 - 12:56

Trave Vierendeel

In questo esercizio analizziamo una trave Vierendeel, la quale può essere rappresentata con un modello Shear-Type messo in orizzontale;
questo schema è caratterizzato da elementi talmente compatti che posso considerarli corpi rigidi, ricordando le due ipotesi fondamentali:
 
  • La trave è infinitamente resistente a flessione (momento di inerzia molto alto)
  • I pilastri non si deformano se sottoposti ad un qualsiasi sforzo normale
Analizziamo il modello, calcolandone gli spostamenti (quindi la deformata), i diagrammi del momento e del taglio, sia sugli elementi orizzontali sia su quelli verticali.
 

Come prima cosa calcolo le varie reazioni di taglio, analizzando separatamente ogni tratto (o asta verticale) della struttura, partendo dall'estremo a sinistra.
Ora eseguo il medesimo procedimento per gli altri 5 tratti restanti, ricordandomi sempre di considerare anche le forze già calcolate.

Posso ora disegnare il diagramma del taglio per gli elementi orizzontali:

Per trovare i valori dei momenti, mi basta prendere ciascun valore del taglio e moltiplicarlo rispettivamente per metà della lunghezza l/2 (poiché in quei punti, nelle mezzerie, ho i valori nulli del diagramma momento).

Deformata:

Ora, mi mancano solo momento e taglio nelle aste verticali.
per il momento, mi basta calcolare l'equilibrio al nodo di ciascun elemento:
Fatto ciò, posso trovare anche i valori dei tagli, calcolando l'equilibrio di ciascuna asta verticale:

In ultimo, disegno i due diagrammi:

Taglio

Momento

Verifico ora questo risultati con SAP2000:

Taglio

Momento

Deformata

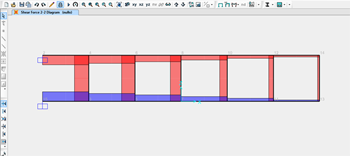
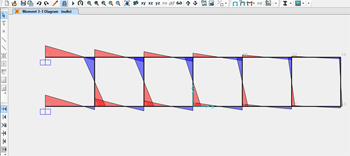
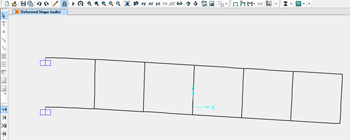
Anche se con qualche differenza quantitativa e diversa convenzione di segno, i risultati corrispondono.

Trave Vierendeel_caso 2

In questo esercizio analizziamo nuovamente la trave Vierendeel, questa volta però vincolata a entrambi i bordi, calcolandone gli spostamenti (quindi la deformata), e calcolandone anche qui, gli spostamenti (quindi la deformata), i diagrammi del momento e del taglio, sia sugli elementi orizzontali sia su quelli verticali.

 

Un aspetto che posso sfruttare, è la simmetria della struttura.
Ora come prima cosa calcolo le varie reazioni di taglio, analizzando separatamente ogni tratto (o asta verticale) della struttura, partendo da quella centrale.

Ora eseguo il medesimo procedimento per gli altri 2 tratti restanti (sfrutto la simmetria), ricordandomi sempre di considerare anche le forze già calcolate.

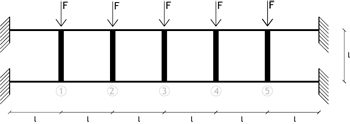
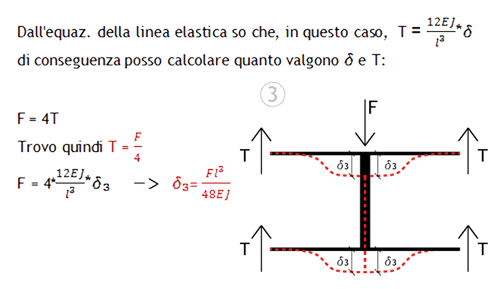
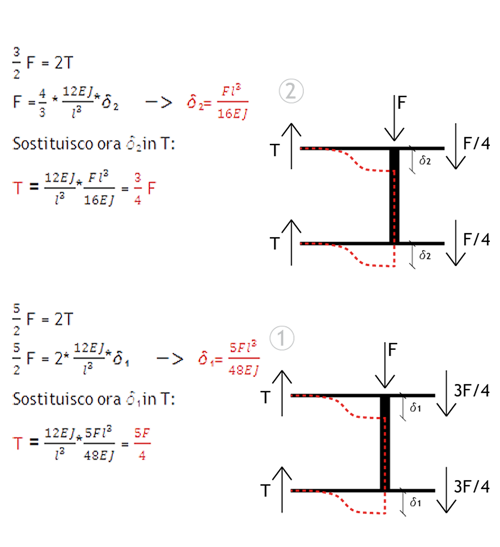
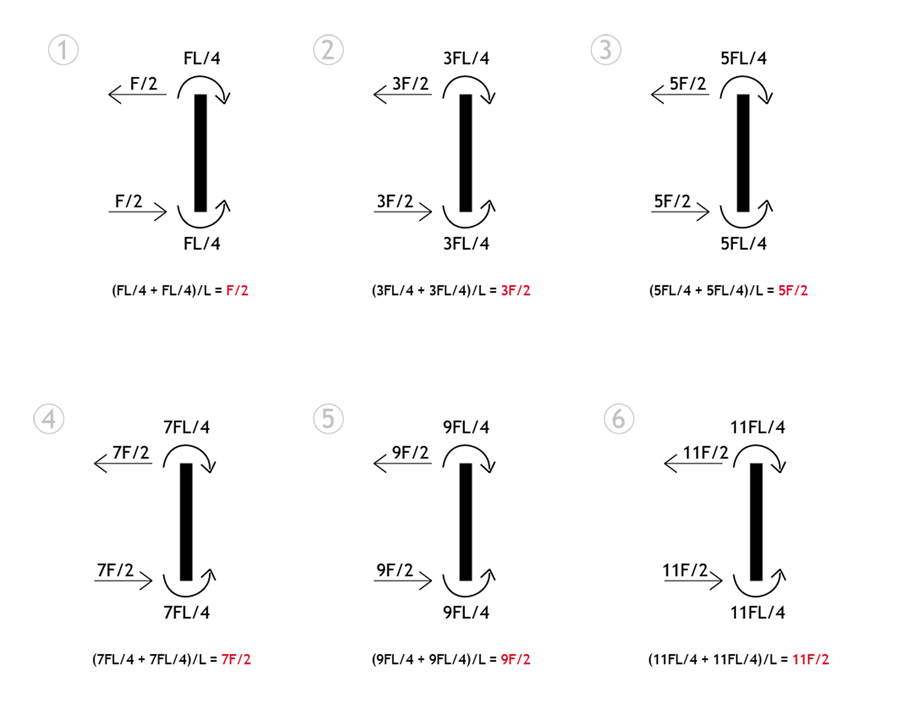
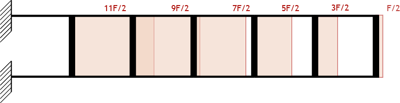
Posso ora disegnare il diagramma del taglio per gli elementi orizzontali:

Per trovare i valori dei momenti, mi basta anche qui prendere ciascun valore del taglio e moltiplicarlo rispettivamente per metà della lunghezza l/2.

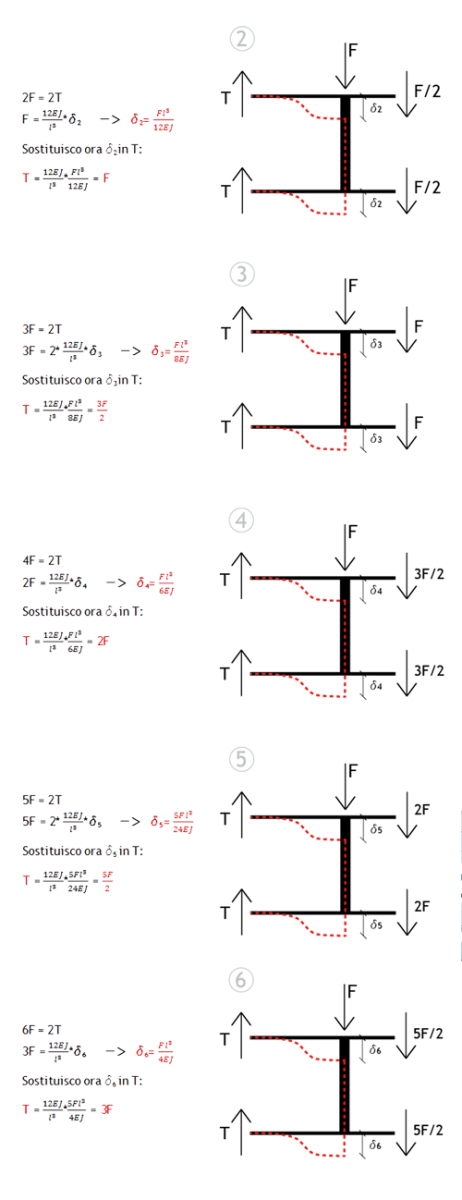
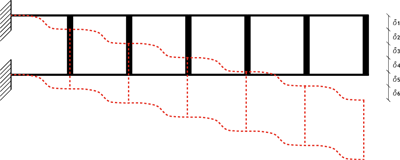
Deformata:

 

Ora, mi mancano solo momento e taglio nelle aste verticali.
per il momento, mi basta calcolare l'equilibrio al nodo di ciascun elemento:

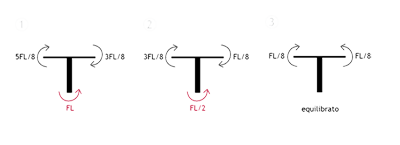
Fatto ciò, posso trovare anche i valori dei tagli, calcolando l'equilibrio di ciascuna asta verticale (ricordando che l'asta centrale non ha né momento, né taglio):

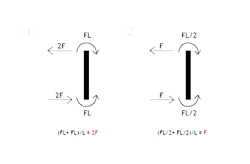
Disegno i diagrammi:

Taglio

Momento

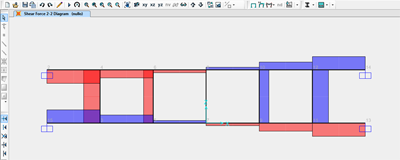
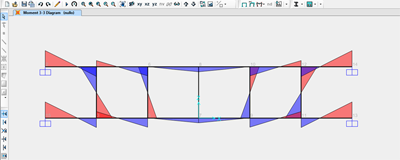
Verifico ora questo risultati con SAP2000:

Taglio

Momento

Deformata

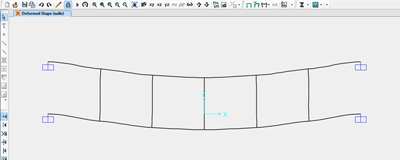
Anche se con qualche differenza quantitativa e diversa convenzione di segno, i risultati corrispondono.