blog di dario.taffi

Esercitazione VII_Rigidezza torsionale

Inviato da dario.taffi il Sab, 01/06/2013 - 12:47

Esercizio I

In questa esercitazione cercheremo di risolvere una struttura tridimensionale, 12 volte iperstatica, composta da un nodo con tre aste incastrate all’estremità e una mensola con carico distribuito.
Al contrario di altre volte, in questo caso avremo a che fare con due componenti: flessione e torsione. 
Come primo passo, posso eliminare la mensola, sostituendola con il suo momento in corrispondenza del nodo. Al contrario, non terrò conto dello sforzo normale a cui è soggetto il pilastro, poichè lo considero sempre assialmente indeformabile.
                                      
Ora, il problema sta nel fatto che questo momento sottopone le aste ad una rotazione, la quale a sua volta provoca delle rigidezze flessionali nelle aste AB e AC, e una rigidezza torsionale nell'asta AD.
                                    

Ipotizzando (come nelle esercitazioni precedenti) che il nodo A in questione ceda anelasticamente a rotazione, posso risolvere l'iperstaticità della struttura tramite il metodo della linea elastica (e trovare così i valori dei momenti).

                                   
Quindi (aggiungendo il momento torsionale dell'asta AD):
                                     
L'equazione di equilibrio dei momenti è la seguente:
dalla quale ricavo la rotazione 
Dove RA è la somma di tutte le rigidezze.
 
Rispettivamente i momenti saranno: 

Ora, scelgo un profilo per le aste, in modo tale da calcolarmi i vari valori.
Dati:
l1= 2m
l2= 4m
l3= 4m
l4= 3m

Profilo acciaio: 

E=1,999*108 kN/m2
I= 5,554*10-5 m4
Gsteel= 80*106 kN/m2
 
It(ala)= 22,47 *10-8 m4
It(anima)= 5,66 *10-8 m4
It = 50,6 * 10-8 m4
 
 
 

 

Ora posso calcolare come si distribuisce il momento su ogni asta (in base alla rigidezza):

Verifico in SAP2000 questi risultati:
 
Deformata
 
Momenti:

I risultati corrispondono.

Cambiando la sezione dell'asta soggetta a torsione, il momento si ripartisce diversamente:

 
Verifico in SAP2000 questi risultati:
 
Deformata
 
Momenti:
 

I risultati corrispondono.

Un ultimo tentativo che possiamo fare è utilizzare un profilo in cls, per mettere a confronto i due materiali. Prendo quindi una sezione di questo tipo:
E=24,86*106 kN/m2
I= 3,76*10-3 m4
Gcls= 107 kN/m2
 
It = c2*a*b3     c2= a/b = 0,291
It= 6,58 *10-4 m4
 
 

Il risultato è praticamente identico all'esempio precedente in acciaio, solo con una sezione tre volte più alta.

Esercizio II

Con un procedimento analogo, posso risolvere un graticcio di travi, dove per graticcio si intende un intreccio di travi ortogonali fra loro, che collaborano per contrastare i pesi. In questo caso si tratta di una struttura costituita da una serie di elementi identici (assenza di una gerarchia), infatti un graticcio è distinguibile da una struttura classica per due aspetti: da una parte l’analisi del momento d’inerzia delle travi (questo è identico per ciascuna trave essendo, dall'altra l'importanza in questo caso della torsione.
 
Per capire meglio questi concetti, prendo in esame due aste perpendicolari tra loro a l/3, con una forza concentrata nel nodo. 
Come in altri casi, questo sistema (teoricamente) possiede 6 g.d.l., ma considerando le aste sempre indeformabili, posso trascurare gli spostamenti in direzione x e y e le rotazioni intorno gli assi z e x.

Quindi, mi rimangono solo 2 g.d.l. (δ e ϕy) che posso ricavarmi con le equazioni di equilibrio alla traslazione verticale e alla rotazione.

 

Attraverso la sovrapposizione degli effetti di δ e ϕy, trovo l’equilibrio alla traslazione e alla rotazione:

         

 

 
 
Equilibrio alla traslazione verticale:

             

 
Equilibrio alla trotazione:

             

Dall'equazione dei momenti ricavo δ in funzione di ϕy:

  dove  
 
Sostituendo δ/l nell'equazione dell'equilibrio alla traslazione, posso ricavare ϕy:
 
 
A questo punto posso decidere un materiale e una sezione (per comodità di calcoli utilizzo la stesso profilo IPE utilizzato nell'esercitazione precedente)

Profilo acciaio: 

 

            E=1,999*108 kN/m2
            J= 5,554*10-5 m4
            Gsteel= 80*106 kN/m2
            Jt = 50,6 * 10-8 m4
 
 
 
 
 
 
 
Sostituisco i valori sopra riportati e ottengo:
 

Infine ricavo il valore dei momenti agenti sulla struttura:

 
Verifico con SAP2000 i valori ottenuti:
 
Momento
Torsione
 
Ripeto le stesse operazioni utilizzando il profilo in cls dell'esercitazione precedente:
 
E=24,86*106 kN/m2 
J= 3,76*10-3 m4
Gcls= 107 kN/m2
Jt= 6,58 *10-4 m4
 
 
 
 
 
 
 
 
 
 
 
 
 
 
Sostituisco i valori sopra riportati e ottengo:
 

Infine ricavo il valore dei momenti agenti sulla struttura:

 
Verifico con SAP2000 i valori ottenuti:
 
Momento
Torsione
 

Esercitazione VI_Ripartizione forze sismiche

Inviato da dario.taffi il Gio, 09/05/2013 - 21:38
In questa esercitazione viene affrontato l'aspetto delicato dell'esistenza delle azioni orizzontali (troppo spesso non considerate...) in natura (azione sismica, vento, ecc.).
L'aspetto importante da tenere in considerazione è il fatto che i medesimi elementi strutturali possono avere una doppia funzione, (a patto che siano disposti in maniera intelligente nello spazio. Nella pratica, un insieme di travi e pilastri, se allineati in un piano verticale,  rappresentano allo stesso tempo una struttura che sopporta i carichi verticali ma anche le azioni orizzontali (controvento).
 

Detto ciò, prendiamo in considerazione un piano "tipo" (simile a quello del progetto su cui sto lavorandocon Federico Restaino nel Lab. 2M, definito dal seguente impalcato (pianta strutturale):

Ipotizziamo che l’impalcato sia in calcestruzzo armato (quindi con modulo elastico E=21000 N/mm2) e sia composto da 18 pilastri aventi sezione rettangolare e dimensioni 30x40 cm. Dato che una sezione rettangolare ha due momenti d’inerzia, uno lungo l’asse x e l’altro lungo l’asse y, i pilastri sono stati disposti in base alla tessitura del solaio.

Quindi:
Ix= bh3/12 = 90000,00 cm4  (pilastri A1, A2, B1, B2, C1, C2, D1, E1)
Iy= hb3/12 = 160000,00 cm4  (pilastri D2, D3, D4, D5, D6, E2, E3, E4, E5, E6)
 
Osservando l'impalcato, individuiamo 11 telai piani, 6 lungo Y e 5 lungo X. Questi hanno il compito (oltre a portare il peso della costruzione), anche di controventare la struttura intera, cioè di resistere a forze orizzontali.

Ora, essendo i controventi degli elementi con comportamento elastico, possono essere semplificati come delle vere e proprie molle...

Utilizzeremo ora un foglio Excell, grazie al quale ripartiremo la forza orizzontale (in particolare quella sismica) sui controventi, attribuendone ad ognuno una frazione, che è il rapporto della rigidezza del controvento e della sua distanza da un punto privilegiato (il centro delle rigidezze C).
 
Passo 1: Calcolo delle rigidezze traslanti dei controventi dell'edificio
Come prima cosa, calcoliamo la rigidezza traslante di ogni controvento, quindi tenendo conto del Modulo di elasticità (E), dell’altezza dei pilastri (h) e del momento d’inerzia di ogni pilastro (I). 

Passo 2: Tabella sinottica controventi e distanze

Ora calcoliamo le distanze verticali (dv) e orizzontali (do) dei controventi dal punto O, che è l’origine del nostro sistema di riferimento.

Passo 3: Calcolo del centro di massa
Per calcolare il centro di massa G, dividiamo la struttura in due aree, la più grande di 254,15 m2 e la più piccola di 120 m2.
 

Successivamente inserendo nella tabella la misura di ogni superficie e le coordinate dei relativi baricentri (mantenendo l’origine O come riferimento), otteniamo le coordinate del centro di massa G:
Xg = (A1 x Xg1+ A2 x Xg2) / (A1 + A2)
Yg = (A1 x Yg1+ A2 x Yg2) / (A1 + A2)
 

Passo 4: Calcolo del centro delle rigidezze e delle rigidezze globali
Ora con la tabella troviamo il centro delle rigidezze C, ovvero il punto in cui ruota la struttura se nasce un momento; dopodichè calcoliamo le distanze di ogni controvento dal centro delle rigidezze e infine la rigidezza torsionale totale (la sommatoria di ogni rigidezza moltiplicata per la distanza al quadrato dal centro delle rigidezze).
 

 
Passo 5: Analisi dei carichi sismici

Inserendo una serie di valori (coefficiente di contemporaneità Ψ, coefficiente di intensità sismica c,...) obbligatori da normativa, otteniamo il calcolo della forza sismica orizzontale, che nella nostra struttura è pari a 300,09 KN.

 
Passo 6-7: Ripartizione della forza sismica lungo X e Y
Poichè la forza sismica è applicata nel centro di massa G, che molto spesso non coincide con il centro delle rigidezze C (come in questo caso), avviene una torsione della struttura in quanto si genera un braccio tra i punti G e C (ovviamente, maggiore sarà il braccio e maggiore sarà la rotazione dell’impalcato). 

Le ultime due tabelle calcolano il momento torcente della struttura, le traslazioni e le rotazioni secondo le due direzioni perpendicolari.

Lungo X
 
Lungo Y

Esercitazione V_Trave Vierendeel

Inviato da dario.taffi il Sab, 27/04/2013 - 12:56

Trave Vierendeel

In questo esercizio analizziamo una trave Vierendeel, la quale può essere rappresentata con un modello Shear-Type messo in orizzontale;
questo schema è caratterizzato da elementi talmente compatti che posso considerarli corpi rigidi, ricordando le due ipotesi fondamentali:
 
  • La trave è infinitamente resistente a flessione (momento di inerzia molto alto)
  • I pilastri non si deformano se sottoposti ad un qualsiasi sforzo normale
Analizziamo il modello, calcolandone gli spostamenti (quindi la deformata), i diagrammi del momento e del taglio, sia sugli elementi orizzontali sia su quelli verticali.
 

Come prima cosa calcolo le varie reazioni di taglio, analizzando separatamente ogni tratto (o asta verticale) della struttura, partendo dall'estremo a sinistra.
Ora eseguo il medesimo procedimento per gli altri 5 tratti restanti, ricordandomi sempre di considerare anche le forze già calcolate.

Posso ora disegnare il diagramma del taglio per gli elementi orizzontali:

Per trovare i valori dei momenti, mi basta prendere ciascun valore del taglio e moltiplicarlo rispettivamente per metà della lunghezza l/2 (poiché in quei punti, nelle mezzerie, ho i valori nulli del diagramma momento).

Deformata:

Ora, mi mancano solo momento e taglio nelle aste verticali.
per il momento, mi basta calcolare l'equilibrio al nodo di ciascun elemento:
Fatto ciò, posso trovare anche i valori dei tagli, calcolando l'equilibrio di ciascuna asta verticale:

In ultimo, disegno i due diagrammi:

Taglio

Momento

Verifico ora questo risultati con SAP2000:

Taglio

Momento

Deformata

Anche se con qualche differenza quantitativa e diversa convenzione di segno, i risultati corrispondono.

Trave Vierendeel_caso 2

In questo esercizio analizziamo nuovamente la trave Vierendeel, questa volta però vincolata a entrambi i bordi, calcolandone gli spostamenti (quindi la deformata), e calcolandone anche qui, gli spostamenti (quindi la deformata), i diagrammi del momento e del taglio, sia sugli elementi orizzontali sia su quelli verticali.

 

Un aspetto che posso sfruttare, è la simmetria della struttura.
Ora come prima cosa calcolo le varie reazioni di taglio, analizzando separatamente ogni tratto (o asta verticale) della struttura, partendo da quella centrale.

Ora eseguo il medesimo procedimento per gli altri 2 tratti restanti (sfrutto la simmetria), ricordandomi sempre di considerare anche le forze già calcolate.

Posso ora disegnare il diagramma del taglio per gli elementi orizzontali:

Per trovare i valori dei momenti, mi basta anche qui prendere ciascun valore del taglio e moltiplicarlo rispettivamente per metà della lunghezza l/2.

Deformata:

 

Ora, mi mancano solo momento e taglio nelle aste verticali.
per il momento, mi basta calcolare l'equilibrio al nodo di ciascun elemento:

Fatto ciò, posso trovare anche i valori dei tagli, calcolando l'equilibrio di ciascuna asta verticale (ricordando che l'asta centrale non ha né momento, né taglio):

Disegno i diagrammi:

Taglio

Momento

Verifico ora questo risultati con SAP2000:

Taglio

Momento

Deformata

Anche se con qualche differenza quantitativa e diversa convenzione di segno, i risultati corrispondono.

Esercitazione IV_Metodo delle forze per la risoluzione di una struttura iperstatica

Inviato da dario.taffi il Mar, 16/04/2013 - 22:35

Metodo delle forze - Struttura iperstatica

 
Questa struttura è tre volte iperstatica (posso però semplificare i calcoli sfruttando la simmetria).
Per risolverla, quindi trovare le reazioni vincolari, la trasformo in una struttura isostatica, togliendo un grado di vincolo in B, C e D, permettendo quindi in quei punti la rotazione.

Così facendo "tiro fuori" le reazioni vincolari interne dei momenti X1, X2, X3 (dove X1 = X3 per simmetria).

Ora devo imporre le nuove condizioni di vincolo:
DfiB=0
DfiC=0
DfiD=0
 
Questo significa che devo calcolarmi ora nei tre punti le rotazioni f, provocate sia dal carico q, sia dai momenti X1, X2, X3(ponendo sempre la condizione  Dfisinistra=Dfidestra in B, C e D).
Per simmetria:
Ora, trovo X1, X2, mettendo insieme i valori di destra e di sinistra ottenuti nei rispettivi punti:
 
e sostituendo ottengo anche: 
 
Ora, conoscendo X1, X2, X3, posso trovare le reazioni vincolari:    

  • prima in relazione al carico q:

 
  • poi in relazione ai momenti X1, X2, X3:
 
  • facendo le dovute somme:
 
  • Posso unire il tutto trovando le reazioni vincolari finali:
 
 
Infine, disegno i diagrammi del taglio e del Momento, trovandone i valori nei diversi punti.
 
Taglio
 
 
Momento:  

 

Esercitazione III_Analisi dei carichi e dimensionamento di una trave (acciaio, legno, cls)

Inviato da dario.taffi il Gio, 11/04/2013 - 17:33
Come prima cosa, ho definito il telaio strutturale. 
In seguito, ho scelto di progettare la trave del solaio sottoposta a maggior carico, ovvero la trave A-B lungo l’allineamento 2.

 

Analisi dei carichi

Voglio sapere ora, quanto pesa il solaio e in particolare, quanto carico andrà sulla trave che sto analizzando.

 

Tipologie di carico:

 

  • Carico strutturale (qs = Kg/mq): corrisponde al peso proprio di tutti gli elementi strutturali.
  • Carico permanente (qp = Kg/mq): tiene in considerazione il peso dei restanti elementi che compongono il pacchetto solaio (massetto, intonaco, pavimento,impianti...)
  • Carico accidentale (qa = Kg/mq): strettamente legato alla funzione dell’edificio (considera la variazione dei carichi mobili come arredi, persone,...che possono esserci o meno nel corso del tempo.

Poter progettare la trave principale si deve tener conto, all’interno dei carichi strutturali, anche del peso dei travetti, quindi è necessario dimensionare prima i travetti del solaio, tenendo conto di tutti i carichi citati in precedenza.

SOLAIO IN ACCIAIO

Progetto travetti

Travetti (interasse 1 m, luce 3.85 m)

Carico strutturale (Qs)
 
  
 
  • Lamiera grecata A75-P570 (h: 0.75 m) + gettata in cls (s: 0.15m)  ->   2.50 kN/m²
Qs: 2.50 kN/m²
Calcolo Carico Proprio Permanente (Qp)                                                   
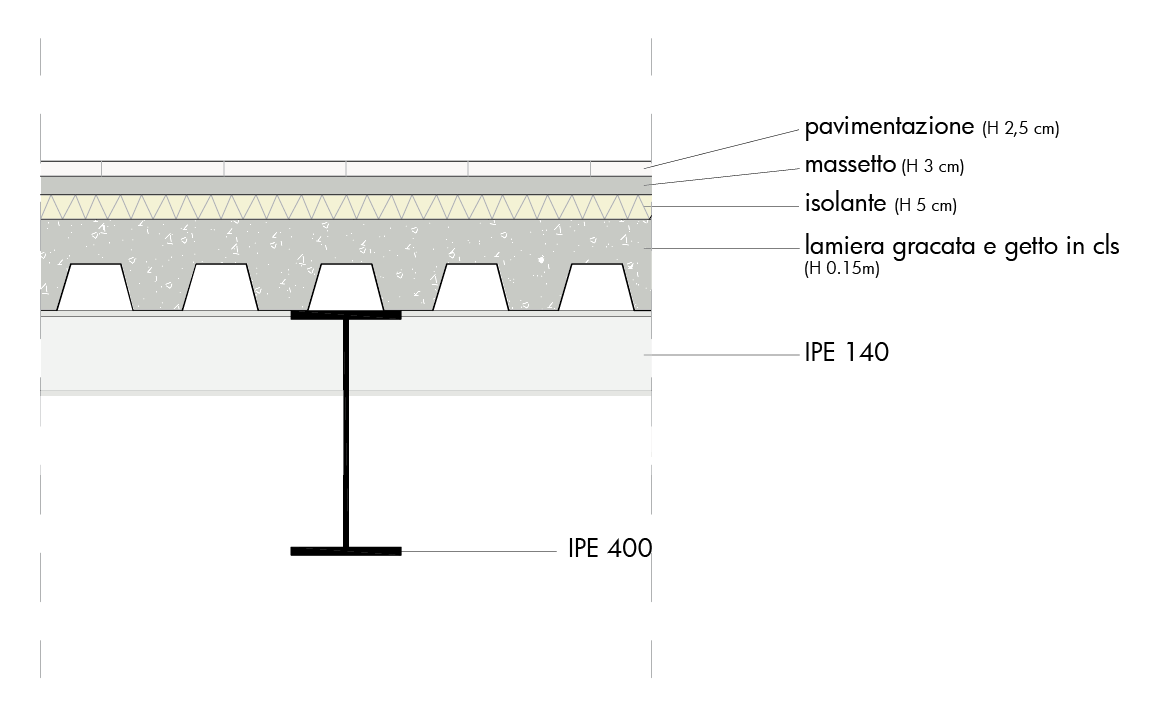
  • Isolante: 0.12 kN/m²
  • Massetto: 24kN/m³ * 0.03m: 0.72 kN/m²
  • Pavimentazione in legno di abete bianco: sp.: 0.025m , peso specifico 340 kg/m²:(0.025*1*1)*3.4= 0.85 kN/m²
  • Tramezzi e impianti: 1.5 kN/m²                                          
 Qp: 0.12+0.75+0.85+1.5= 3.19 kN/m²
Calcolo Carico Accidentale (Qa)
  • Ambiente ad uso residenziale: 2.00 kN/m² da normativa
Qa:2.00 kN/m²

Trovati i valori per i differenti tipi di carico, inserisco nel foglio Excell i risultati, la luce della trave e il suo interasse. Avendo deciso di utilizzare un acciaio Fe360/S235, inserisco il suo valore caratteristico a snervamento che equivale a 235 N/mm2. 
 
Risultati Excell:
interasse (m)
qs (KN/m2)
qp (KN/m2)
qa (KN/m2)
q (KN/m)
luce (m)
M (KN*m)
fy,k (N/mm2)
sigam (N/mm2)
Wx (cm3)
1
2,5
3,19
2,00
7,69
 3,85
14,2481
235
204,35
69,72
Il modulo di resistenza minimo per i travetti è 69.09 cm3.
Scelgo delle IPE 140 (W = 77.3 cm3).
 
Ora eseguo la verificacon l'aggiunta del peso dei travetti:
peso proprio travetto: 0,129 KN/m:
peso travetto al m²: 0,129 KN/m / 1m (interasse)= 0.129 kN/m²

Qs*: 2.50+0.129= 2.629 kN/m²

Risultati Excell:
interasse (m)
qs (KN/m2)
qp (KN/m2)
qa (KN/m2)
q (KN/m)
luce (m)
M (KN*m)
fy,k (N/mm2)
sigam (N/mm2)
Wx (cm3)
1
2,629
3,19
2,00
7,819
3,85
14,4871
235
204,35
70,89

Verificato: travetti: IPE 140  (W = 77.3 cm3 > 70.89 cm3)

Progetto trave

Luce (L): 7.7m
Interasse (i): 3.85m
Area d'influenza:  29.65m²
 

Calcolo Carico Proprio Strutturale (Qs)                                                            

  • Travetti: IPE 140   12.9 kg/m : 0.129 kN/m²
  • Lamiera grecata A55-P600 (h: 0.75 m) + gettata in cls (s: 0.15m)  ->   2.50 kN/m²
Qs: 2.5+0.129= 2.629 kN/m²
Calcolo Carico Proprio Permanente (Qp)                                                   
  • Isolante: 0.12 kN/m²
  • Massetto: 24kN/m³ * 0.03m: 0.72 kN/m²
  • Pavimentazione in legno di abete bianco: sp.: 0.025m , peso specifico  340 kg/m²: (0.025*1*1)*3.4= 0.85 kN/m²
  • Tramezzi e impianti: 1.5 kN/m²                                          
    Qp: 0.12+0.75+0.85+1.5= 3.19 kN/m²
Calcolo Carico Accidentale (Qa)
  • Ambiente ad uso residenziale: 2.00 kN/m² da normativa
Qa:2.00 kN/m²
 
Trovati i valori per i differenti tipi di carico, inserisco nel foglio Excell i risultati, la luce della trave e il suo interasse. Avendo deciso di utilizzare un acciaio Fe360/S235, inserisco il suo valore caratteristico a snervamento che equivale a 235 N/mm2.
 
Risultati Excell:
interasse(m)
qs(KN/m2)
qp(KN/m2)
qa(KN/m2)
q(KN/m)
luce(m)
M (KN*m)
fy,k(N/mm2)
sigam (N/mm2)
Wx (cm3)
3,85
2,629
3,19
2,00
30,1032
7,7
223,102
235
204,35
1091,78
Il modulo di resistenza minimo per i travetti è di 1091,78 cm3.

Scelgo delle IPE 400 (W = 1160 cm3).

Ora eseguo la verificacon l'aggiunta del peso della trave:
peso proprio trave: 0.776 KN/m:
peso trave al m²: 0,776 KN/m / 3.85m (interasse)= 0.202 kN/m²

Qs*: 2.629+0.202= 2.831 kN/m²

Risultati Excell:

 

interasse(m)
qs KN/m2)
qp (KN/m2)
qa (KN/m2)
q(KN/m)
luce(m)
M(KN*m)
fy,k(N/mm2)
sigam(N/mm2)
Wx(cm3)
3,85
2,831
3,19
2,00
30,8809
7,7
228,866
235
204,35
1119,98

Verificato: IPE 400 (Wx: 1160 cm³  > 1119,98 cm³)

SOLAIO IN LEGNO

Similmente effettuo la stessa operazione per dimensionare una trave lignea.
Anche in questo caso per progettare la trave principale si deve tener conto, all’interno dei carichi strutturali, anche del peso dei travetti, quindi è necessario dimensionare prima i travetti.
 
Progetto travetti
 

Travetti (interasse 1 m, luce 3.85 m)

Carico strutturale (Qs)
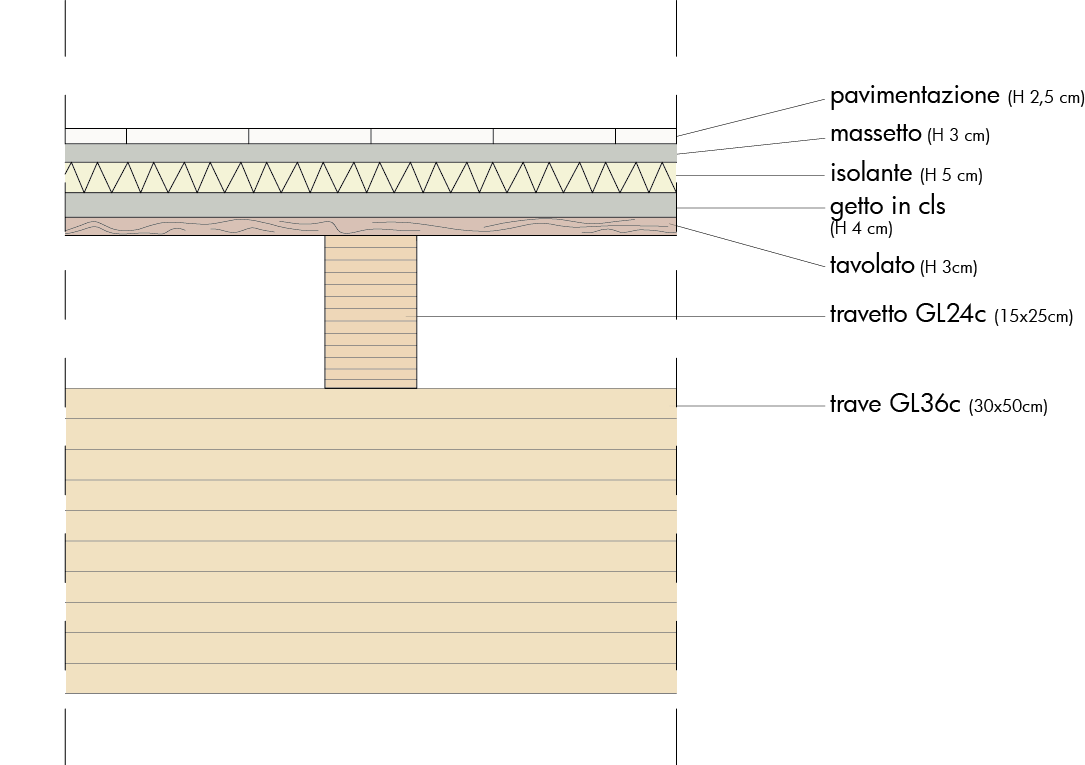
  • tavolato in legno s: 0.03m peso 6 kN/m²:0.03*1*7 ->  0.18 KN/mq

Qs: 0.18 kN/m²

Carico permanente non strutturale (Qp):                   
  • Gettata di cls: peso specifico 20kN/m²,s: 0.04 m -> 0.8 kN/m²
  • Isolante acustico: 0.075 kN/m²
  • Massetto: 24 kN/m²x 0.03 m: 0.72 kN/m²
  • Pavimentazione in legno di abete bianco: sp.: 0.025m , peso specifico  340 kg/m²: (0.025*1*1)*3.4= 0.85 kN/m²
  • Tramezzi e impianti: 1.5 kN/m²               
                         Qp: 0.8+0.075+0.72+0.85+1.5= 3.945 KN/mq
 
Calcolo Carico Accidentale (Qa)
  • Ambiente ad uso residenziale: 2.00 kN/m² da normativa
Qa:2.00 kN/m²

 

Trovati i valori per i differenti tipi di carico, inserisco nel foglio Excell i risultati, la luce della trave, il suo interasse.
Ipotizzo inoltre, un travetto in legno lamellare GL24c (Fm,k:24N/mm²).
 
 
Da normativa scelgo un kmod:0.60 (derivante da una classe di servizio 1, e una classe di durata del carico permanente, ipotizzando una classica abitazione).
 
 
Risultati Excell:
interasse(m)
qs(KN/m2)
qp(KN/m2)
qa(KN/m2)
q(KN/m)
luce(m)
M (KN*m)
fm,k(N/mm2)
kmod
sigamN/mm2)
b(cm)
h(cm)
1
0,18
3,945
2,00
6,125
3,85
11,34848
24
0,6
9,93
15
21,38

Avendo ipotizzato una base di 15cm, ottengo un'altezza di 21,38cm, che per motivi convenzionali approssimerò a 25 cm (quindi travetto: GL24c 15*25 cm)

Ora posso effettuare la verifica inserendo anche il peso proprio dei travetti:
peso specifico GL24c: 350 kg/m³
peso travetto:(3,50* 0.15*0.2*3.85)= 0.4 kN

peso travetto al m²: 0,4 KN/1m (interasse)/3.85 (luce)= 0.10 kN/m²

Qs*: 0.18+0.10= 0.28 kN/m²
Risultati Excell:
interasse(m)
qs(KN/m2)
qp(KN/m2)
qa(KN/m2)
q(KN/m)
luce(m)
M (KN*m)
fm,k(N/mm2)
kmod
sigamN/mm2)
b(cm)
h(cm)
1
0,28
3,945
2,00
6,225
3,85
11,53376
24
0,6
9,93
15
21,55

Verificato: travetti: GL24c  (H = 25 cm > 21.55 cm)

Progetto trave

Luce (L): 7.7m
Interasse (i): 3.85m

Area d'influenza:  29.65m²

Calcolo Carico Proprio Strutturale (Qs)                                                            
  • Travetti: GL24c: 0.10 kN/m²
  • Tavolato in legno s: 0.03m peso 6 kN/m²:0.03*1*7 ->  0.18 KN/mq
Qs: 0.10+0.18= 0.28 kN/m²
Calcolo Carico Proprio Permanente (Qp)                                                   
  • Gettata di cls: peso specifico 20kN/m²,s: 0.04 m -> 0.8 kN/m²
  • Isolante acustico: 0.075 kN/m²
  • Massetto: 24 kN/m²x 0.03 m: 0.72 kN/m²
  • Pavimentazione in legno di abete bianco: sp.: 0.025m , peso specifico  340 kg/m²: (0.025*1*1)*3.4= 0.85 kN/m²
  • Tramezzi e impianti: 1.5 kN/m²                
Qp: 0.8+0.075+0.72+0.85+1.5= 3.945 KN/mq
Calcolo Carico Accidentale (Qa)
  • Ambiente ad uso residenziale: 2.00 kN/m² da normativa
Qa:2.00 kN/m²

Eseguo gli stessi calcoli effettuati per i travetti, adottando stavolta un legno lamellare GL36c (Fm,k:36N/mm²):

Risultati Excell:
interasse(m)
qs(KN/m2)
qp(KN/m2)
qa(KN/m2)
q (KN/m)
luce(m)
M (KN*m)
fm,k(N/mm2)
kmod
sigamN/mm2)
b(cm)
h(cm)
3,85
0,28
3,945
2,00
23,96625
7,7
177,6199
36
0,6
14,90
30
48,83
Avendo ipotizzato una base 30cm, ottengo un'altezza di 48,83cm, che per motivi convenzionali approssimerò a 50 cm (quindi trave: GL36c 30*50 cm).
 
Ora posso effettuare la verifica inserendo anche il peso proprio della trave:
peso specifico GL36c: 430 kg/m³
peso trave:(4,30* 0.3*0.5*7,7)= 4.96 kN
peso trave al m²: 4,96 KN/3,85m (interasse)/7.7 (luce)= 0.17 kN/m²
Qs*: 0.28+0.17= 0.45 kN/m²
Risultati Excell
 
interasse(m)
qs(KN/m2)
qp(KN/m2)
qa(KN/m2)
q (KN/m)
luce(m)
M(KN*m)
fm,k(N/mm2)
kmod
sigamN/mm2)
b(cm)
h(cm)
3,85
0,45
3,945
2,00
24,62075
7,7
182,4705
36
0,6
14,90
30
49,50

Verificato: trave GL36c   (H = 50 cm > 49.50 cm)

SOLAIO IN CLS

Progetto trave

Luce (L): 7.7m
Interasse (i): 3.85m

Area d'influenza:  29.65m²

Calcolo Carico Proprio Strutturale (Qs)        
                                 
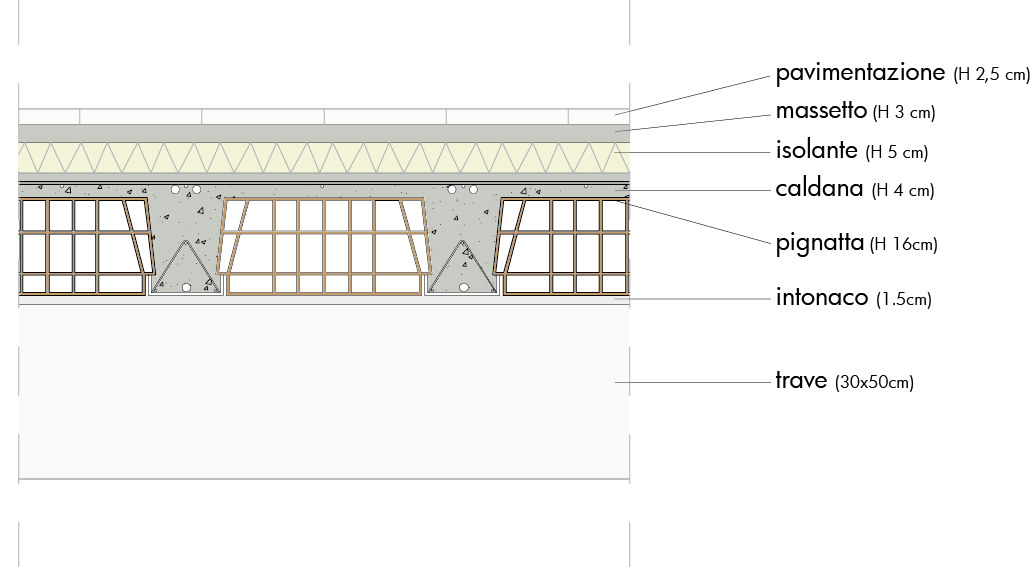
  • Solaio in laterocemento con travetti armati : H 0.2m (0.16+0.04), peso 266 kg/m² -> 2.66 kN/m²
Qs: 2.66 kN/m²
CalcolCarico Proprio Permanente (Qp)                                                   
  • Isolante: 0.12 kN/m²
  • Massetto: 24kN/m³ * 0.03m: 0.72 kN/m²
  • Pavimentazione in legno di abete bianco: sp.: 0.025m , peso specifico  340 kg/m²: (0.025*1*1)*3.4= 0.85 kN/m²
  • Intonaco (s.0.015 cm): 0.3 kN/m²Tramezzi e impianti: 1.5 kN/m²                                                
Qp: 0.12+0.72+0.85+0.3+1.5= 3.49 kN/m²
Calco Carico Accidentale (Qa)
  • Ambiente ad uso residenziale: 2.00 kN/m² da normativa
Qa:2.00 kN/m²
Trovati i valori per i differenti tipi di carico, inserisco nel foglio Excell i risultati, la luce della trave e il suo interasse.
Utilizzo un acciaio B450C per le barre e un cls C35/45 (con Rck: 45 N/mm2).
 
Risultati Excell:
interasse (m)
qs (KN/m2)
qp (KN/m2)
qa(KN/m2)
q (KN/m)
luce (m)
M(KN*m)
fy (N/mm2)
sig_fa (N/mm2)
3,85
2,66
3,49
2,00
31,3775
7,7
232,5465
450
391,30
Rck(N/mm2)
sig_ca(N/mm2)
alfa
r
b (cm)
h (cm)
delta(cm)
H (cm)
H/l
area(m2)
peso(KN/m)
45
25,50
0,49
2,20
30
38,37
5
43,37
0,056
0,13
3,25
Avendo ipotizzato una base 30cm, ottengo un'altezza utile di 38.37cm.
Dovendo aggiungere 5 cm di copriferro e dato che le sezioni standard in calcestruzzo armato hanno dimensioni che variano di 5 cm alla volta, scelgo una sezione di 30 x 45 cm.   
 
Ora eseguo la verifica con l'aggiunta del peso della trave:
peso proprio trave: 3.25 KN/m:
peso trave al m²: 3,25 KN/m / 3.85m (interasse)= 0.84 kN/m²
Qs*: 2.66+0.84=3.5 kN/m²
Risultati Excell:
interasse(m)
qs(KN/m2)
qp (KN/m2)
qa(KN/m2)
q(KN/m)
luce (m)
M((KN*m)
fy(N/mm2)
sig_fa(N/mm2)
3,85
3,5
3,49
2,00
34,6115
7,7
256,5145
450
391,30
Rck(N/mm2)
sig_ca(N/mm2)
alfa
r
b (cm)
h (cm)
delta(cm)
H (cm)
H/l
area(m2)
peso(KN/m)
45
25,50
0,49
2,20
30
40,30
5
45,30
0,059
0,14
3,40
Non verificato: trave cls (H: 45 cm  < 45.30 cm)
Adotto quindi una sezione 30*50 cm

Esercitazione II_Struttura iperstatica

Inviato da dario.taffi il Mer, 03/04/2013 - 23:53

Ora verifico con SAP2000 il risultato:
Come prima cosa, apro un nuovo modello di griglia, dando le seguenti informazioni:

Assegno un carico "nullo" alla struttura, in modo tale che SAP mi calcoli solo l'azione dei carichi e delle forze esterne.

Attraverso il comando Point, disegno un punto a 0,57L (posizione in cui, secondo i miei calcoli, dovrebbe trovarsi la Vmax).

Una volta disegnata la trave e aver assegnato i vincoli, imposto e assegno una sezione.

Assegno un carico distribuito di 20 kN, agente nella direzione della gravità.

Cliccando su "run" (ponendo "do not run case" su DEAD e MODAL) faccio partire l'analisi e posso visualizzare la deformata:

Andando su SHOW FORCES -> FRAMES posso controllare l'azione del Taglio e del Momento e verificarne i valori (i quali corrispondono a quelli calcolati manualmente).
 
Diagramma Taglio

Diagramma Momento

Ora cliccando sul simbolo della casella segnata da una "v" (DISPLAY OPTIONS FOR ACTIVE WINDOW) metto la spunta (nella sezione JOINTS) alla voce "Labels". In questo modo sappiamo quale numero è stato assegnato al nodo.

Per conoscere lo spostamente verticale V in ogni nodo, devo seguire il seguente percorso: DISPLAY -> SHOW TABLES -> selezionare ANALISYS RESULTS, e infine selezionare Joint Displacements:

Esercitazione I_Trave reticolare piana e spaziale

Inviato da dario.taffi il Mer, 03/04/2013 - 23:51
Una travatura reticolare piana è un insieme di aste appartenenti ad uno stesso piano, vincolate l'un l'altra da cerniere interne.
In queste aste è presente solo sforzo normale ed esistono due metodi fondamentali per risolvere questo tipo di struttura:
il metodo delle sezioni di ritter e ilmetodo dei nodi.
 

Nel seguente caso, utilizzo il primo metodo, il quale prevede la sezione di volta in volta di un numero di aste non superiore a tre e dell'analisi delle forze agenti sulle aste in questione.

Come prima cosa trovo le reazioni vincolari:

Ora applico il metodo delle sezioni (Ritter):

sezione I (effettuo i tagli passanti per 3 aste, nei punti in cui ho più incognite "note"):

sezione II

sezione III

Poichè la struttura e le forze che vi agiscono sono simmetriche, posso concludere disegnando il risultato finale:

Ora svolgo la verifica dei risultati su SAP2000:
 
Apro un nuovo modello di trave reticolare su SAP, denominato nel menu TRUSSES.

Assegno un carico "nullo" alla struttura, in modo tale che SAP mi calcoli solo l'azione dei carichi e delle forze esterne.

Imposto e assegno una sezione a tutte le aste.

Assegno un carico di 20kN sull'asse Z (in direzione della gravità) ai nodi superiori della struttura.

Trasformo tutti i nodi in cerniere interne  (Assign -> Frame -> Releases -> Moment33 =0)

Cliccando ora su "run" (ponendo "Do not run case" su DEAD e MODAL) faccio partire l'analisi e posso visualizzare la deformata:

Andando su SHOW FORCES -> FRAMES e impostando AXIAL FORCE posso vedere l'entità dello sforzo normale su ogni asta (i valori corrispondono a quelli calcolati manualmente).

Ora cliccando sul simbolo della casella segnata da una "v" (DISPLAY OPTIONS FOR ACTIVE WINDOW) metto la spunta (su FRAMES) alla voce "Labels". In questo modo sappiamo quale numero è stato assegnato ad ogni asta.

Ora, per conoscere gli sforzi normali di ciascuna asta, devo seguire il seguente percorso: DISPLAY -> SHOW TABLES -> selezionare ANALISYS RESULTS. Nella tabella è possibile osservare, asta per asta, quale è tesa e quale è compressa e di quanto ( i risultati sono ripartiti per le aste ogni 50 cm della loro lunghezza).

Infine, essendo possibile esportare quest'ultima tabella in formato Excel per una eventuale manipolazione dei dati, la modifico lasciando solo i valori che mi interessano e calcolandomi la ơ(N/A)di ciascun elemento.

Il secondo caso è quello di una travatura reticolare spaziale: la modellazione viene effettuata (per comodità e necessità) su AUTOCAD, avendo l’accortezza di non disegnare in layer 0 e di non usare polilinee (dato che dovranno risultare aste separate). 

Il file viene quindi salvato in DXF per poter essere importato in SAP2000. Quest'operazione avviene in SAP con il comando FILE > IMPORT > AutoCAD.dxf File.

Fatto ciò, seleziono l’intero reticolo ed uso Edit> Edit point  > Mmerge joints >  Merge tolerance  >  0,01 (per  impostare un errore nella giunzione delle aste di 1 cm).

Dopodiché assegno i vincoli attraverso il comando Assign  > Joint Restraints, ricordando di utilizzare cerniere e carrelli in modo che non giacciano sullo stesso asse.

Ora assegno un materiale ed una sezione alle aste (Define > Section Properties > Frame sections, scegliendo un tubolare in acciaio di diametro 100mm e spesso 5mm). 

Assegno un carico "nullo" alla struttura, in modo tale che SAP mi calcoli solo l'azione dei carichi e delle forze esterne.

Trasformo tutti i nodi in cerniere interne  (Assign > Frame > Releases > Moment33 =0)

Assegno un carico di 50kN sull'asse Z (in direzione della gravità) ai nodi superiori della struttura.

Cliccando ora su "run" (ponendo "Do not run case" su DEAD e MODAL) faccio partire l'analisi e posso visualizzare la deformata:

Andando su SHOW FORCES -> FRAMES e impostando AXIAL FORCE posso vedere l'entità dello sforzo normale su ogni asta.

Per visualizzare le reazioni vincolari basta andare in Show Forces/Stresses> Joints.

Ora cliccando sul simbolo della casella segnata da una "v" (DISPLAY OPTIONS FOR ACTIVE WINDOW) metto la spunta (su FRAMES) alla voce "Labels". In questo modo sappiamo quale numero è stato assegnato ad ogni asta.

Ora, per conoscere gli sforzi normali di ciascuna asta, devo seguire il seguente percorso: DISPLAY -> SHOW TABLES -> selezionare ANALISYS RESULTS. Nella tabella è possibile osservare, asta per asta, quale è tesa e quale è compressa e di quanto.

Infine, essendo possibile esportare quest'ultima tabella in formato Excel per una eventuale manipolazione dei dati, la modifico lasciando solo i valori che mi interessano e calcolandomi la ơ(N/A)di ciascun elemento.

Abbonamento a Feed RSS - blog di dario.taffi