Esercitazione VI_Ripartizione forze sismiche

Inviato da dario.taffi il Gio, 09/05/2013 - 21:38
In questa esercitazione viene affrontato l'aspetto delicato dell'esistenza delle azioni orizzontali (troppo spesso non considerate...) in natura (azione sismica, vento, ecc.).
L'aspetto importante da tenere in considerazione è il fatto che i medesimi elementi strutturali possono avere una doppia funzione, (a patto che siano disposti in maniera intelligente nello spazio. Nella pratica, un insieme di travi e pilastri, se allineati in un piano verticale,  rappresentano allo stesso tempo una struttura che sopporta i carichi verticali ma anche le azioni orizzontali (controvento).
 

Detto ciò, prendiamo in considerazione un piano "tipo" (simile a quello del progetto su cui sto lavorandocon Federico Restaino nel Lab. 2M, definito dal seguente impalcato (pianta strutturale):

Ipotizziamo che l’impalcato sia in calcestruzzo armato (quindi con modulo elastico E=21000 N/mm2) e sia composto da 18 pilastri aventi sezione rettangolare e dimensioni 30x40 cm. Dato che una sezione rettangolare ha due momenti d’inerzia, uno lungo l’asse x e l’altro lungo l’asse y, i pilastri sono stati disposti in base alla tessitura del solaio.

Quindi:
Ix= bh3/12 = 90000,00 cm4  (pilastri A1, A2, B1, B2, C1, C2, D1, E1)
Iy= hb3/12 = 160000,00 cm4  (pilastri D2, D3, D4, D5, D6, E2, E3, E4, E5, E6)
 
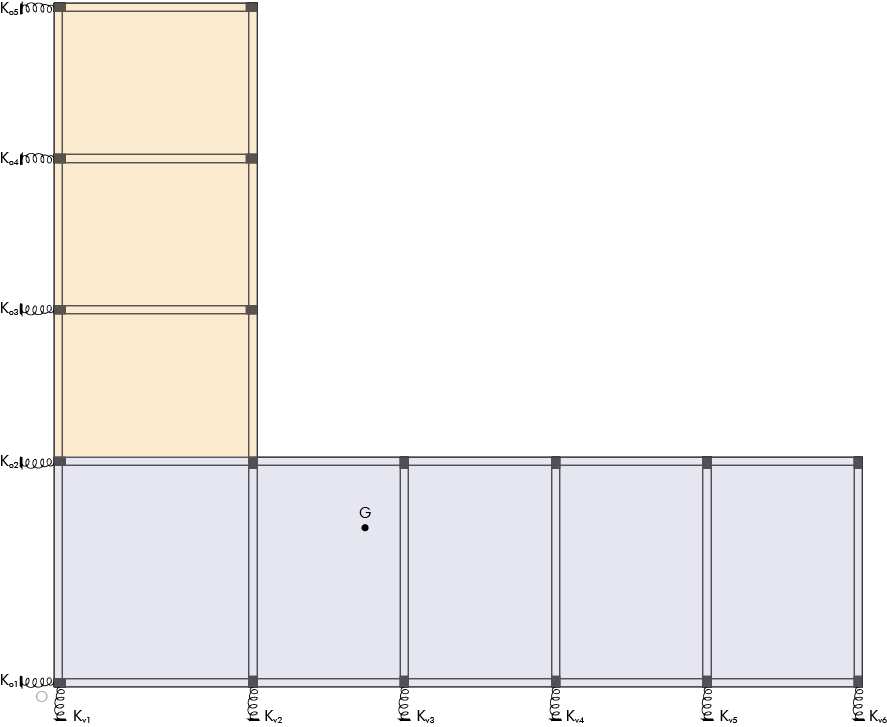
Osservando l'impalcato, individuiamo 11 telai piani, 6 lungo Y e 5 lungo X. Questi hanno il compito (oltre a portare il peso della costruzione), anche di controventare la struttura intera, cioè di resistere a forze orizzontali.

Ora, essendo i controventi degli elementi con comportamento elastico, possono essere semplificati come delle vere e proprie molle...

Utilizzeremo ora un foglio Excell, grazie al quale ripartiremo la forza orizzontale (in particolare quella sismica) sui controventi, attribuendone ad ognuno una frazione, che è il rapporto della rigidezza del controvento e della sua distanza da un punto privilegiato (il centro delle rigidezze C).
 
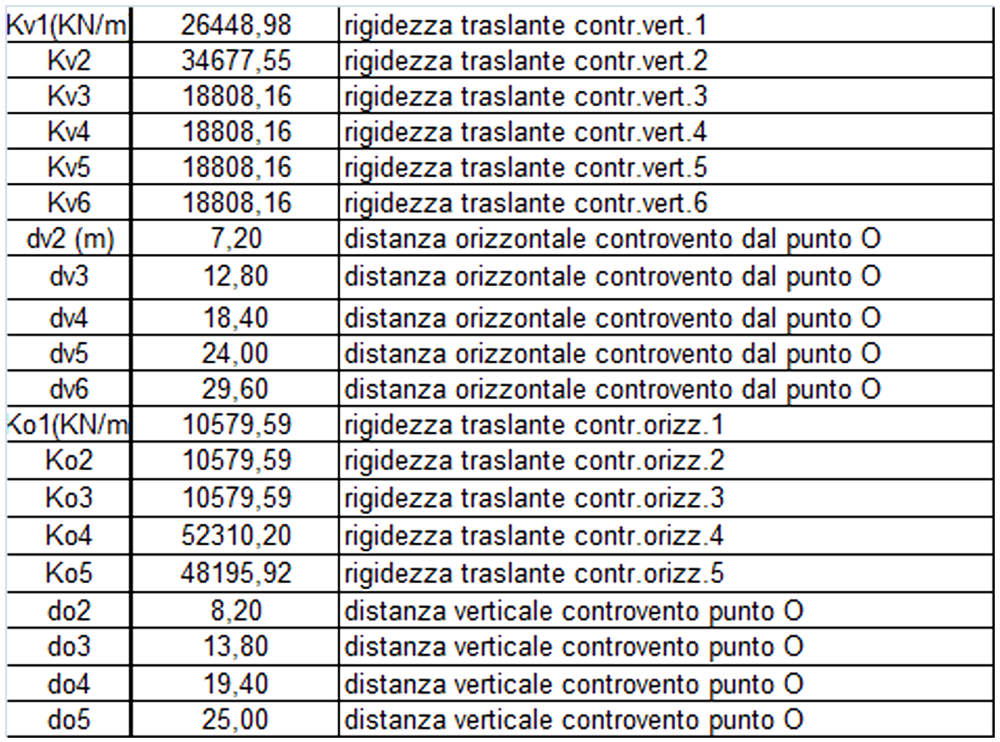
Passo 1: Calcolo delle rigidezze traslanti dei controventi dell'edificio
Come prima cosa, calcoliamo la rigidezza traslante di ogni controvento, quindi tenendo conto del Modulo di elasticità (E), dell’altezza dei pilastri (h) e del momento d’inerzia di ogni pilastro (I). 

Passo 2: Tabella sinottica controventi e distanze

Ora calcoliamo le distanze verticali (dv) e orizzontali (do) dei controventi dal punto O, che è l’origine del nostro sistema di riferimento.

Passo 3: Calcolo del centro di massa
Per calcolare il centro di massa G, dividiamo la struttura in due aree, la più grande di 254,15 m2 e la più piccola di 120 m2.
 

Successivamente inserendo nella tabella la misura di ogni superficie e le coordinate dei relativi baricentri (mantenendo l’origine O come riferimento), otteniamo le coordinate del centro di massa G:
Xg = (A1 x Xg1+ A2 x Xg2) / (A1 + A2)
Yg = (A1 x Yg1+ A2 x Yg2) / (A1 + A2)
 

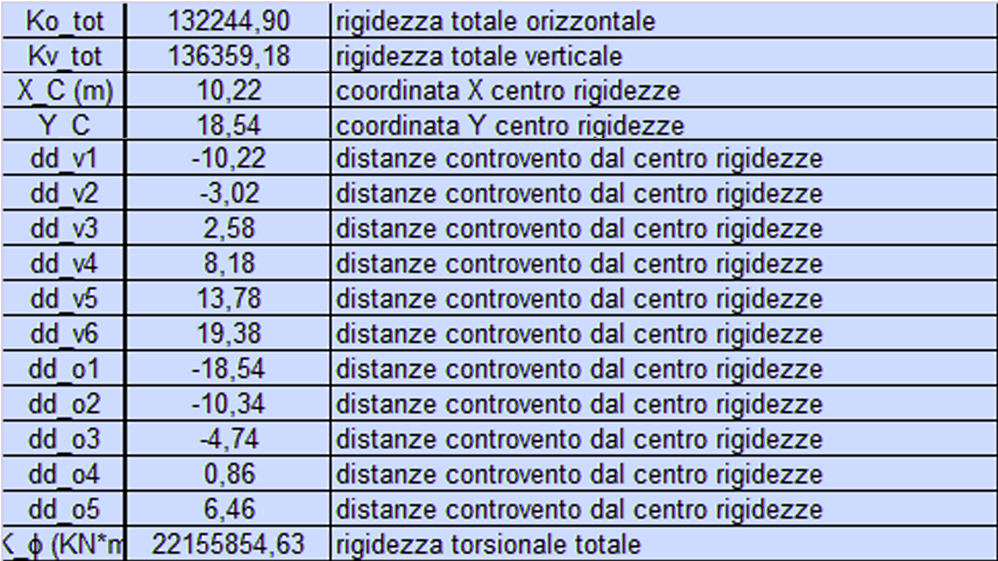
Passo 4: Calcolo del centro delle rigidezze e delle rigidezze globali
Ora con la tabella troviamo il centro delle rigidezze C, ovvero il punto in cui ruota la struttura se nasce un momento; dopodichè calcoliamo le distanze di ogni controvento dal centro delle rigidezze e infine la rigidezza torsionale totale (la sommatoria di ogni rigidezza moltiplicata per la distanza al quadrato dal centro delle rigidezze).
 

 
Passo 5: Analisi dei carichi sismici

Inserendo una serie di valori (coefficiente di contemporaneità Ψ, coefficiente di intensità sismica c,...) obbligatori da normativa, otteniamo il calcolo della forza sismica orizzontale, che nella nostra struttura è pari a 300,09 KN.

 
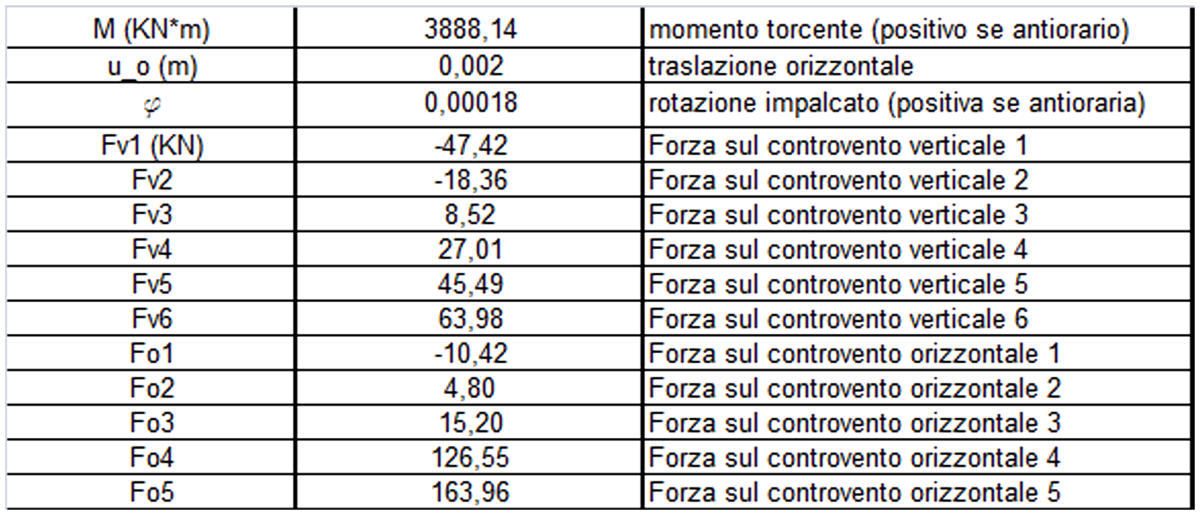
Passo 6-7: Ripartizione della forza sismica lungo X e Y
Poichè la forza sismica è applicata nel centro di massa G, che molto spesso non coincide con il centro delle rigidezze C (come in questo caso), avviene una torsione della struttura in quanto si genera un braccio tra i punti G e C (ovviamente, maggiore sarà il braccio e maggiore sarà la rotazione dell’impalcato). 

Le ultime due tabelle calcolano il momento torcente della struttura, le traslazioni e le rotazioni secondo le due direzioni perpendicolari.

Lungo X
 
Lungo Y