8_ESERCITAZIONE 2 SUL CONCETTO DI RIGIDEZZA_23-04-2013

Il secondo esercizio riguarda una struttura composta sempre da 6 telai shear type sovrapposti e ruotati, ma in questo caso la struttura rimanda ad una trave doppiamente incastrata per via della presenza degli incastri anche sulla destra. Qualitativamente ci aspettiamo risultati almeno in parte diversi e sfruttiamo per i nostri calcoli il concetto di simmetria di cui la struttura gode.

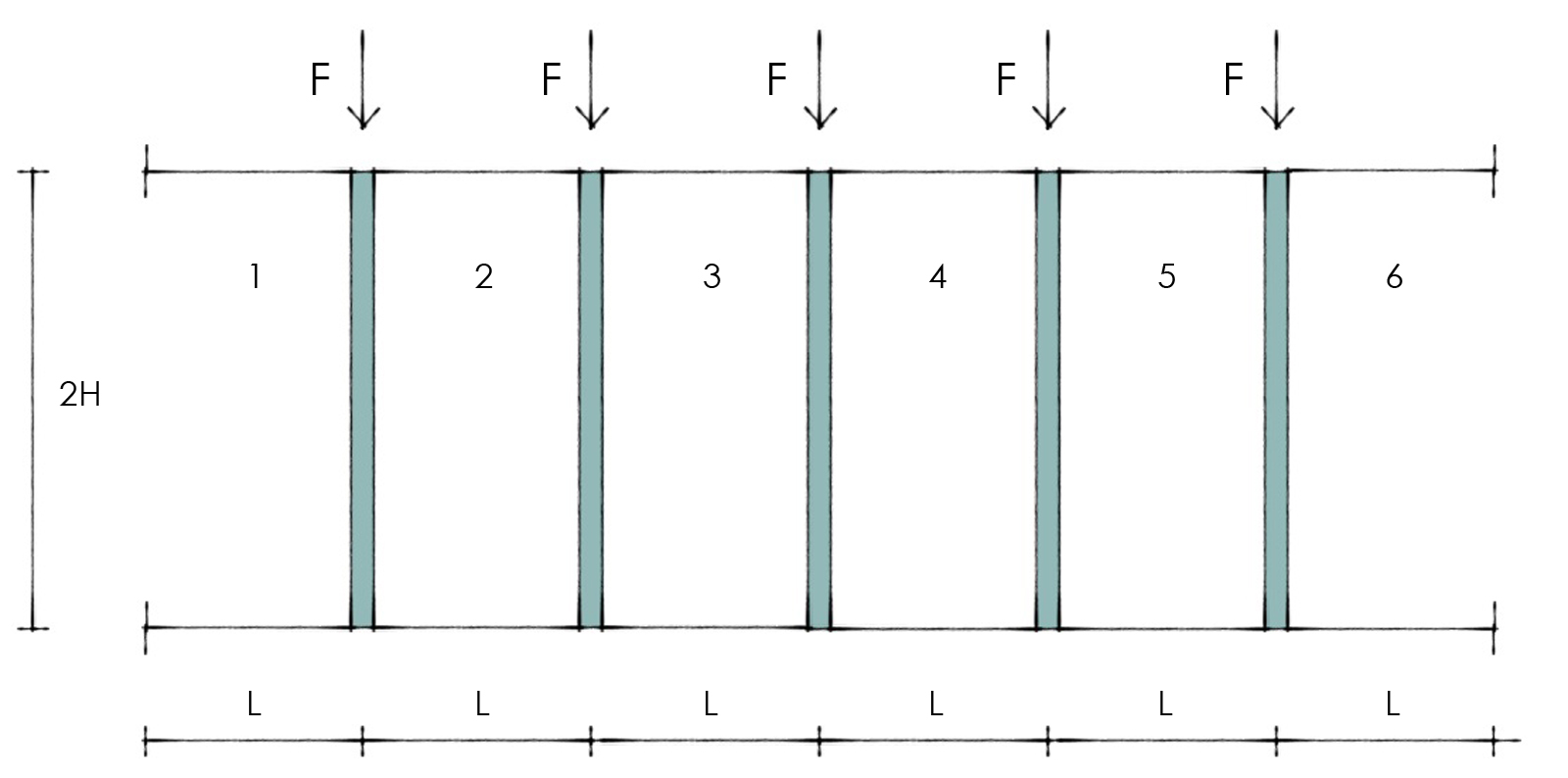
Il primo passo rimane il medesimo rispetto all’esercizio precedente, ossia il calcolo dei valori costanti del Taglio nei pilastri sempre tramite l’equilibrio delle forze orizzontali. Mentre per i telai più esterni non abbiamo particolari problemi, per i due centrali, per la simmetria, dobbiamo avere l’accortezza di ripartire la forza F agente in 4 forze F/4:

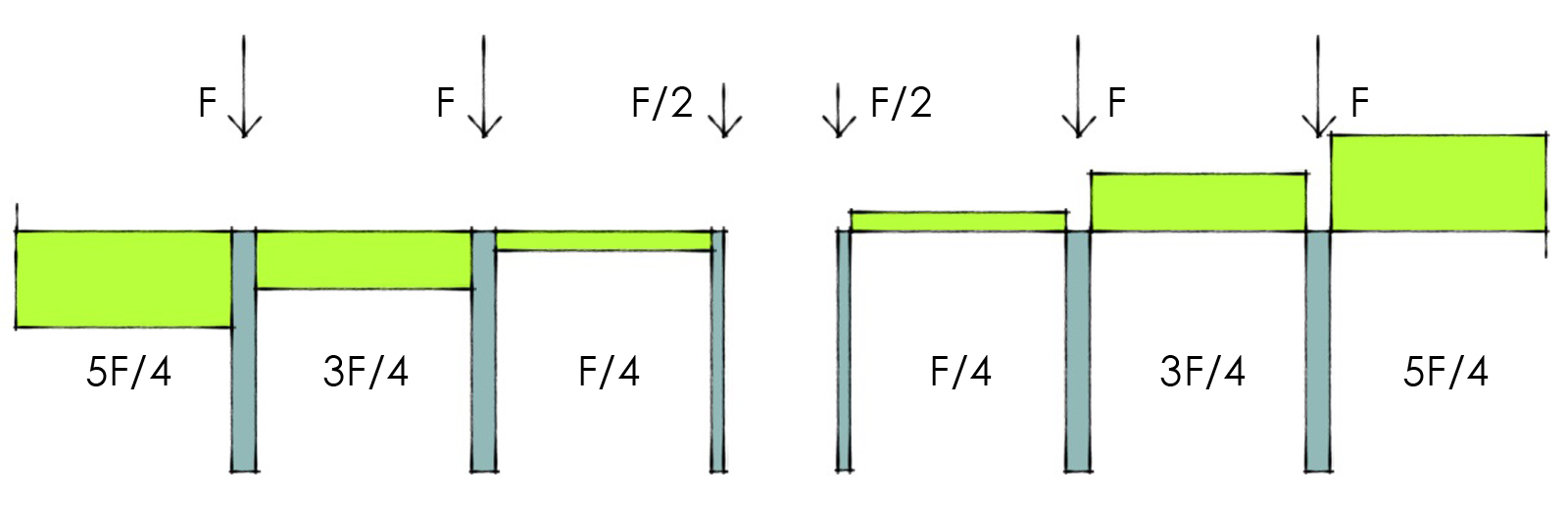
I valori del Taglio ottenuti consentono di calcolare i valori del Momento Flettente massimo negli incastri nei pilastri. Infatti, è sufficiente moltiplicare il valore del taglio nel pilastro in questione per la metà della lunghezza dello stesso:

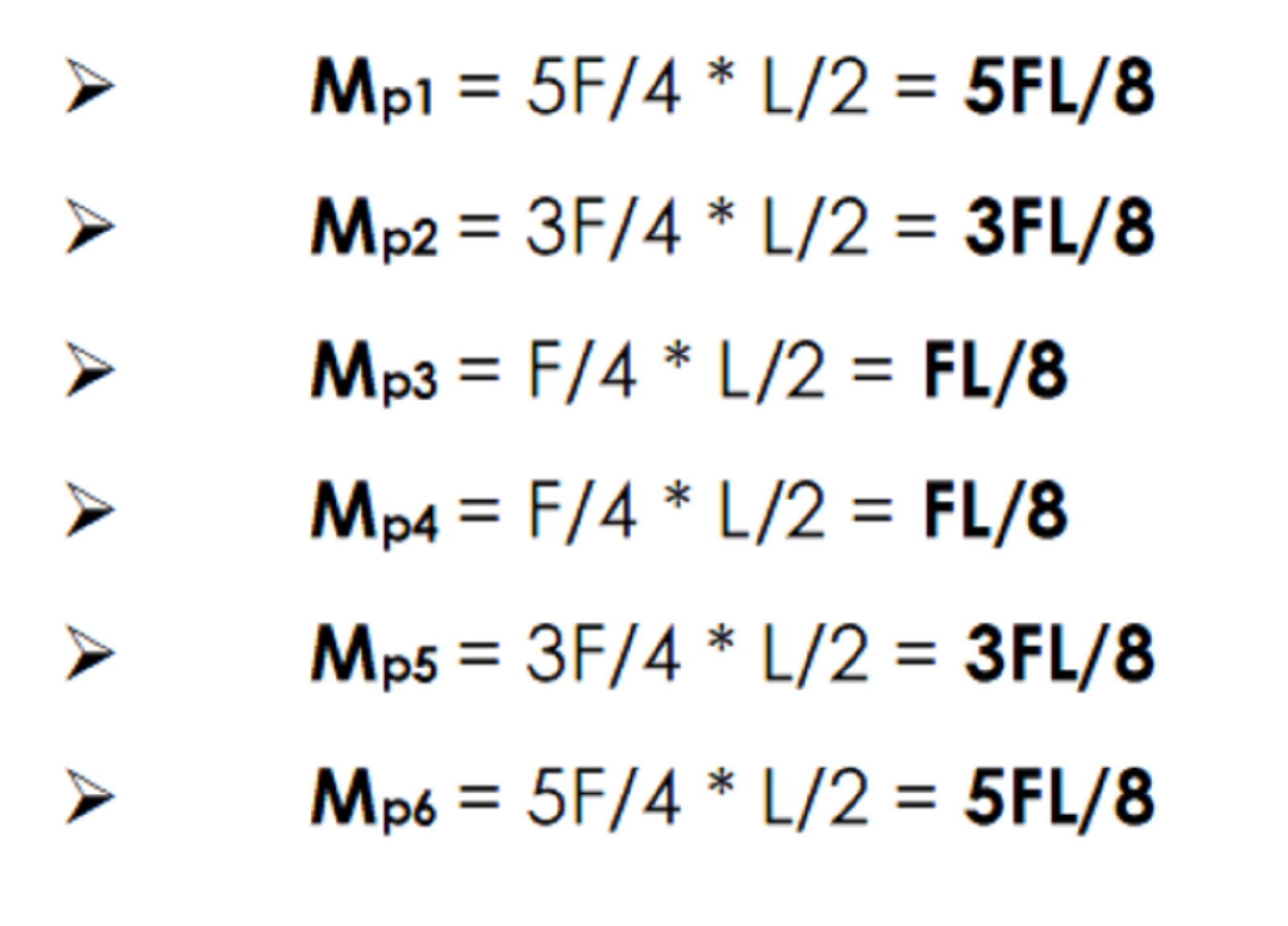
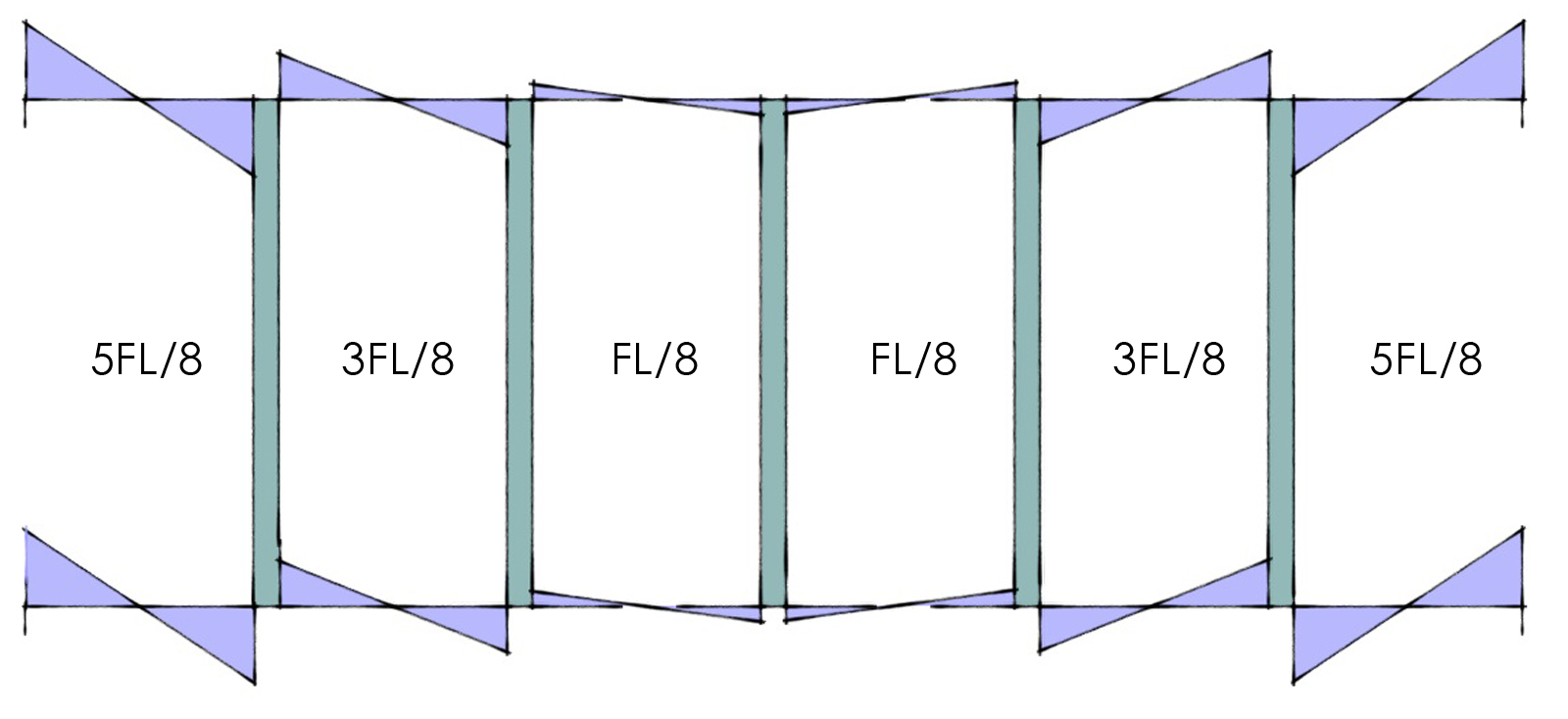
A questo punto passiamo ad analizzare le travi e prima di tutto calcoliamo il loro Momento Flettente sempre mediante l’equilibrio dei momenti nei nodi:

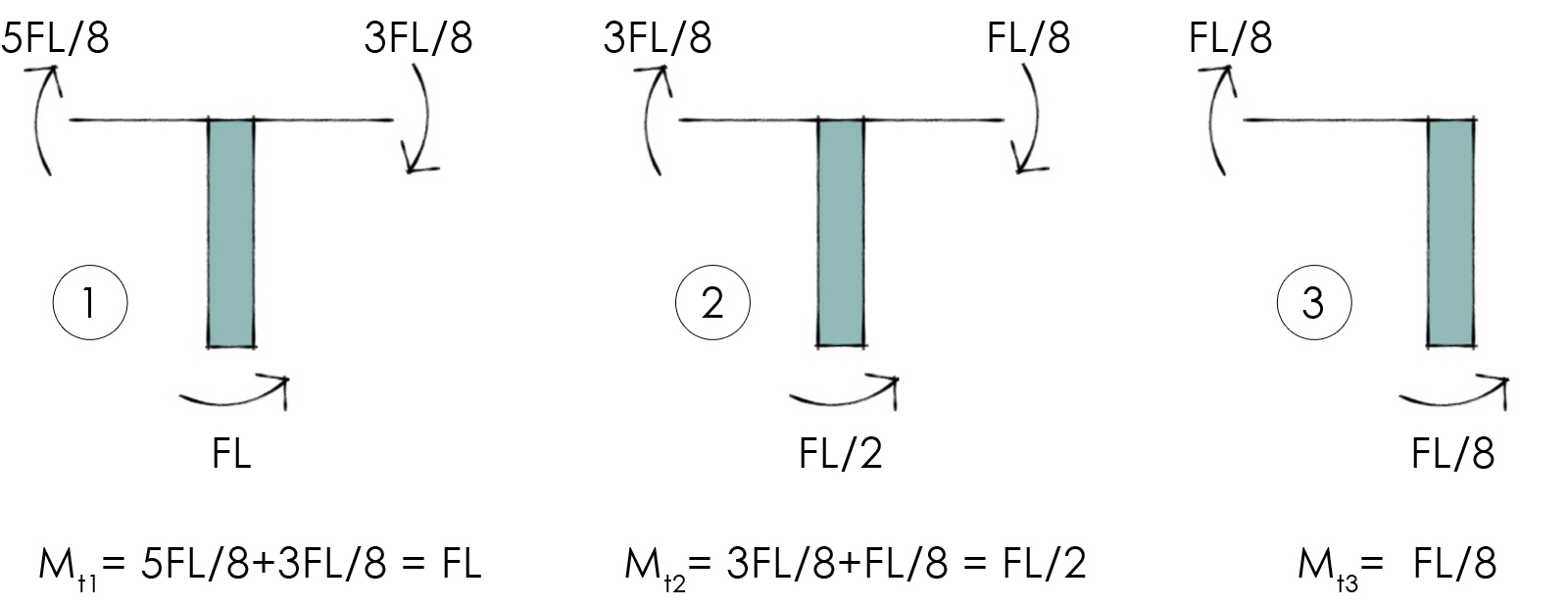
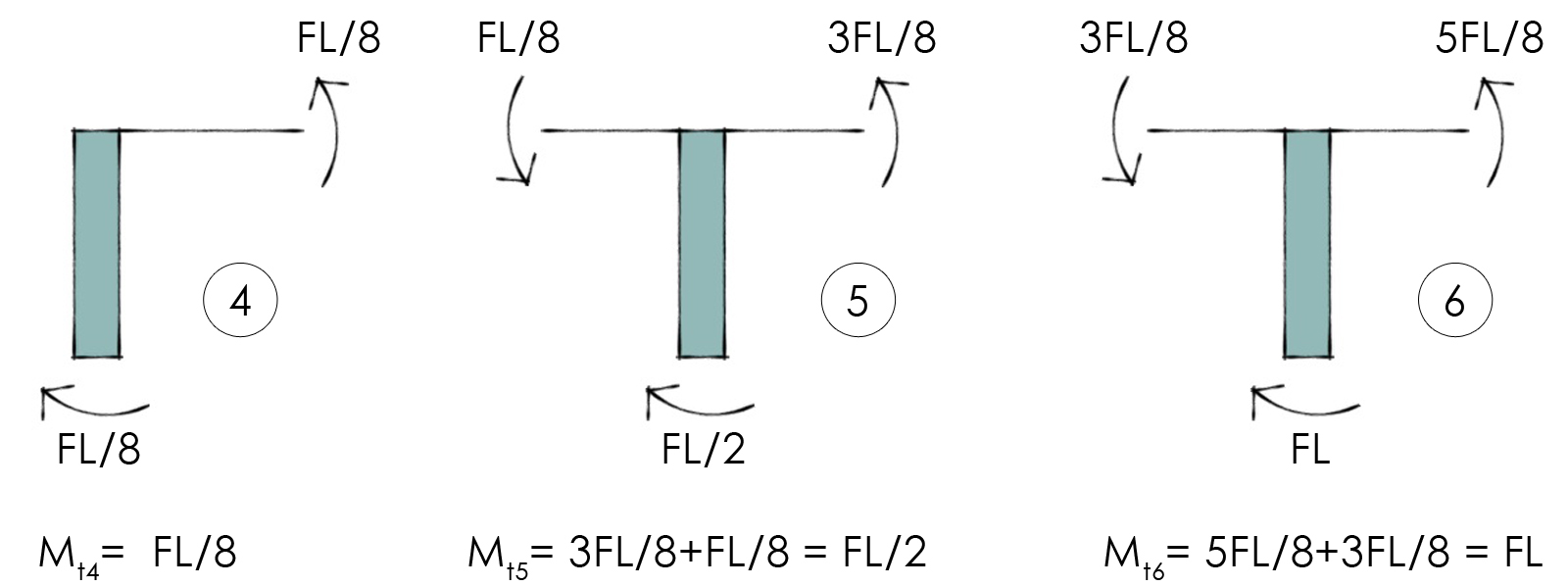
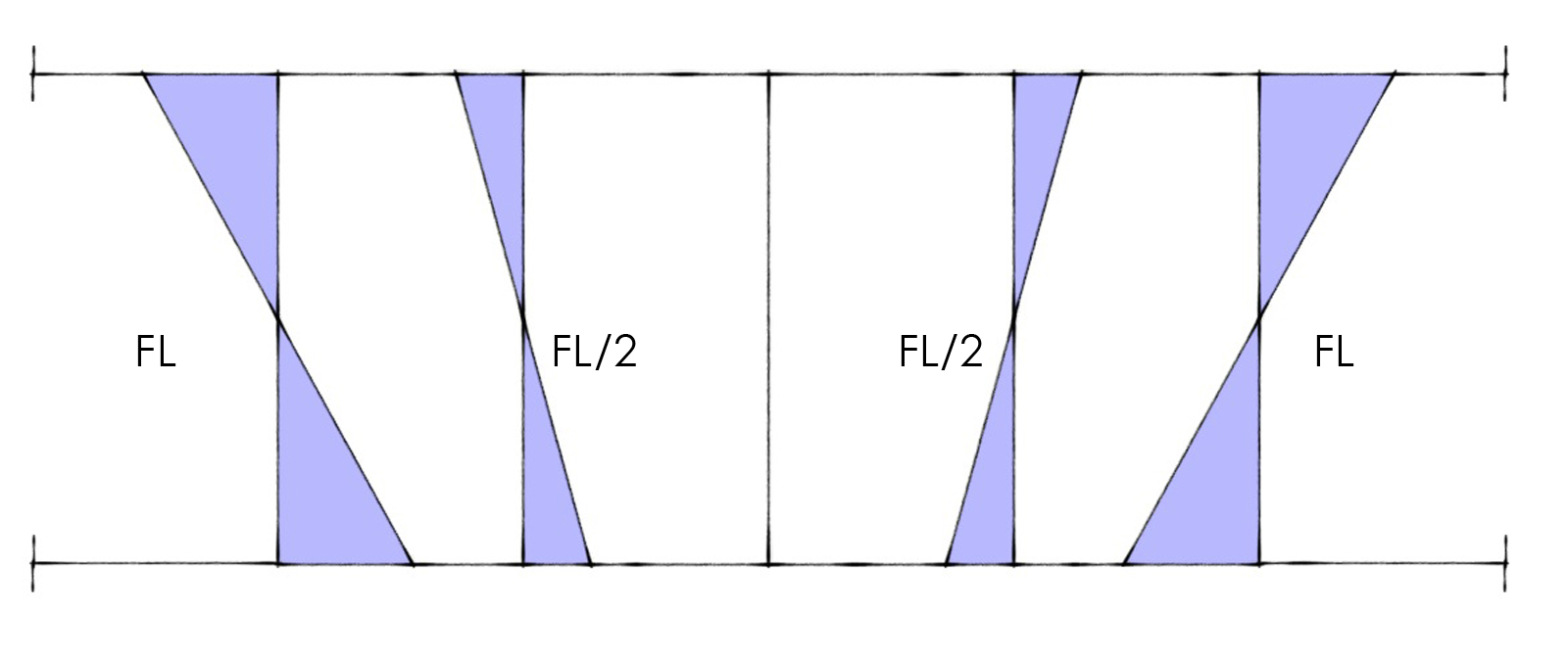
Ora avendo i valori dei Momenti, determiniamo quelli del Taglio nelle travi. Come nell’esercizio analogo precedente i due momenti agli estremi sono concordi, quindi sommiamo i loro valori e dividiamo il risultato ottenuto per la luce, ovvero per il braccio, quantificando così il valore del Taglio:

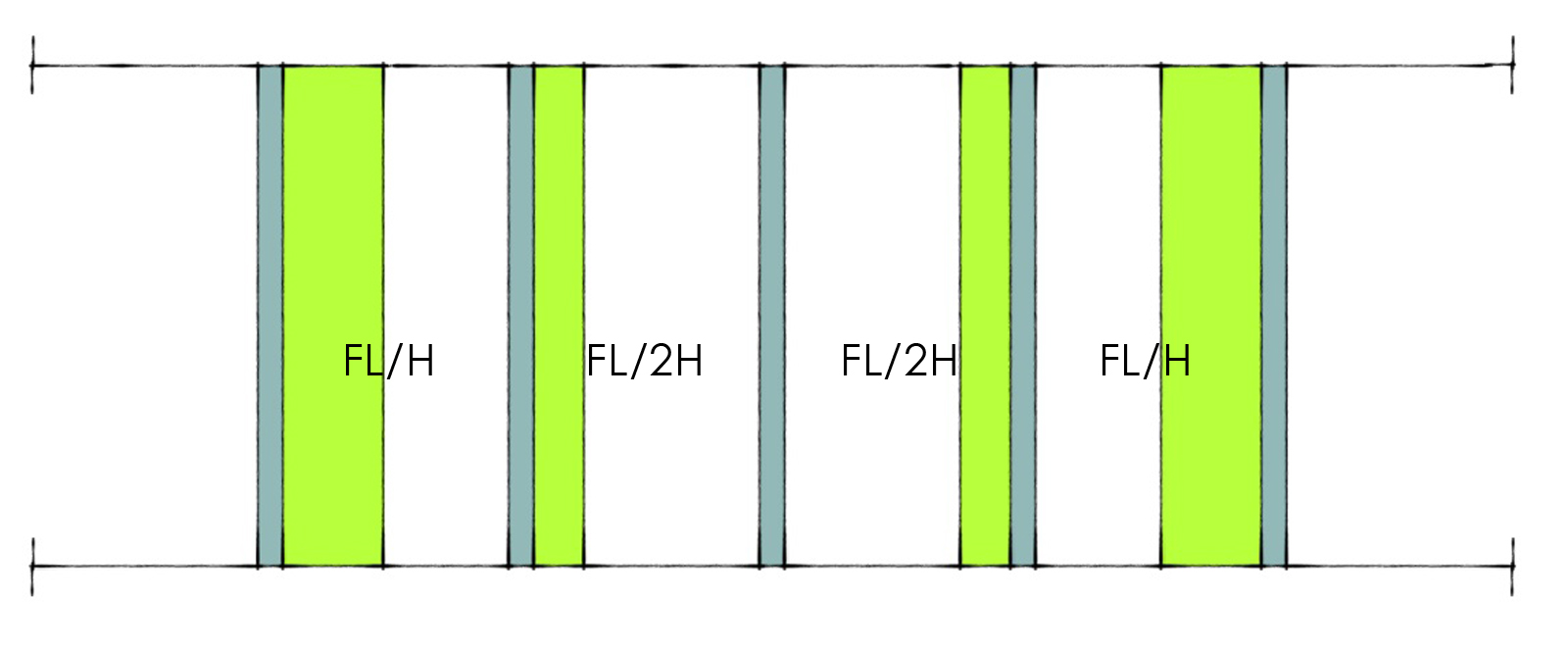
Inutile ripetere come i pilastri abbiano tutti la medesima rigidezza che, dallo studio del telaio shear type, possiamo ritenere uguale a 12EI/L³. A questo punto siamo in possesso di tutti i requisiti utili alla determinazione degli spostamenti. Ancora una volta ci affidiamo all’equilibrio alla traslazione orizzontale del corpo rigido identificato con la trave:

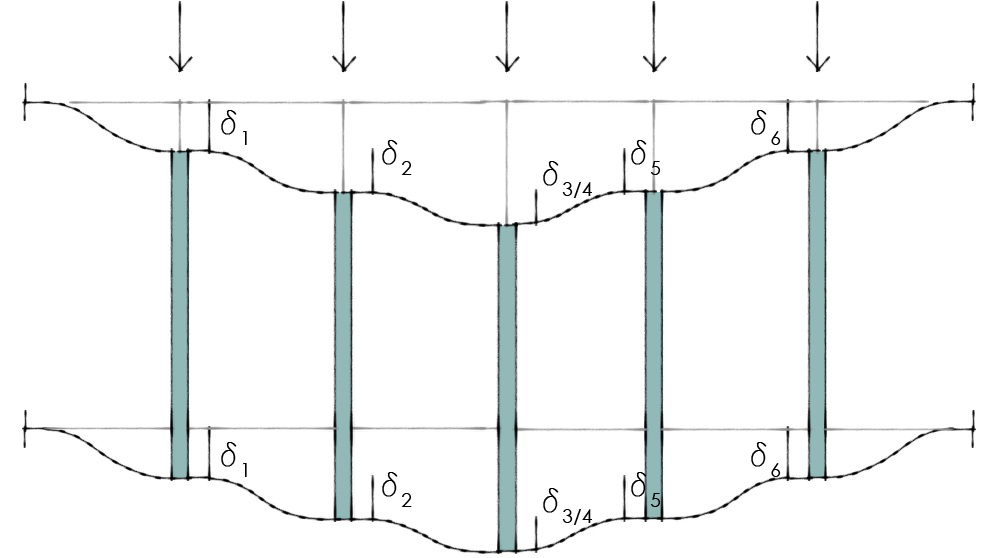
VERIFICA SU SAP

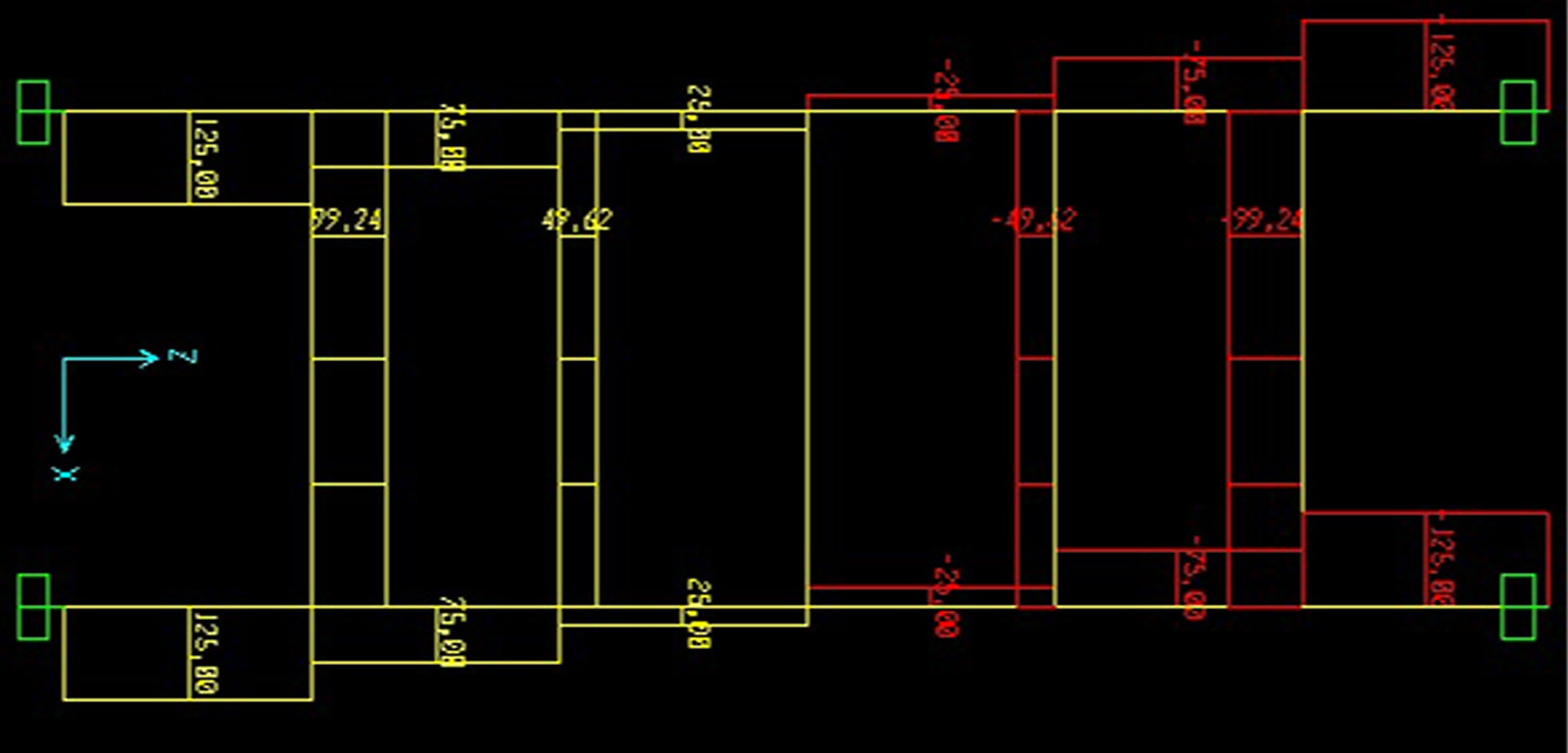
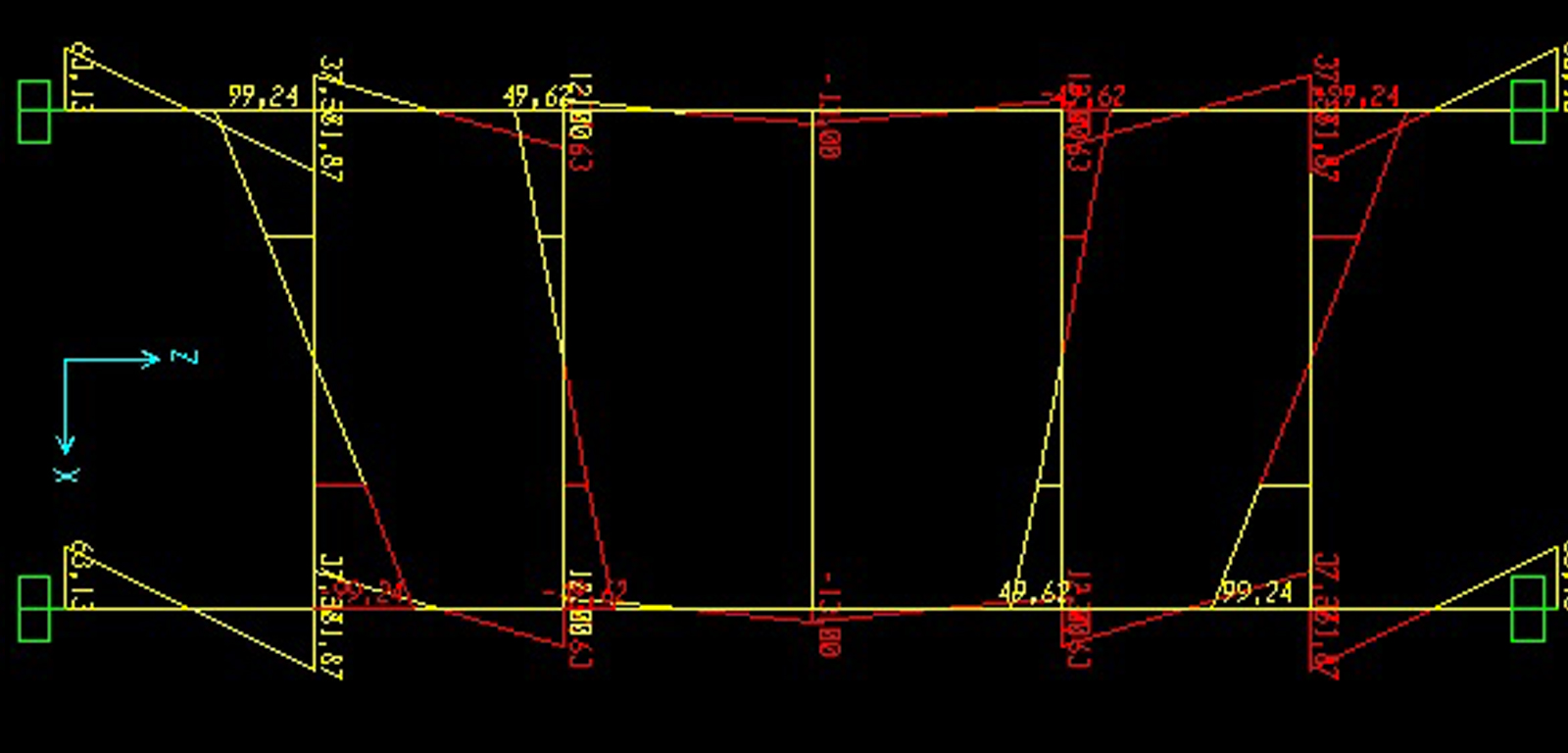
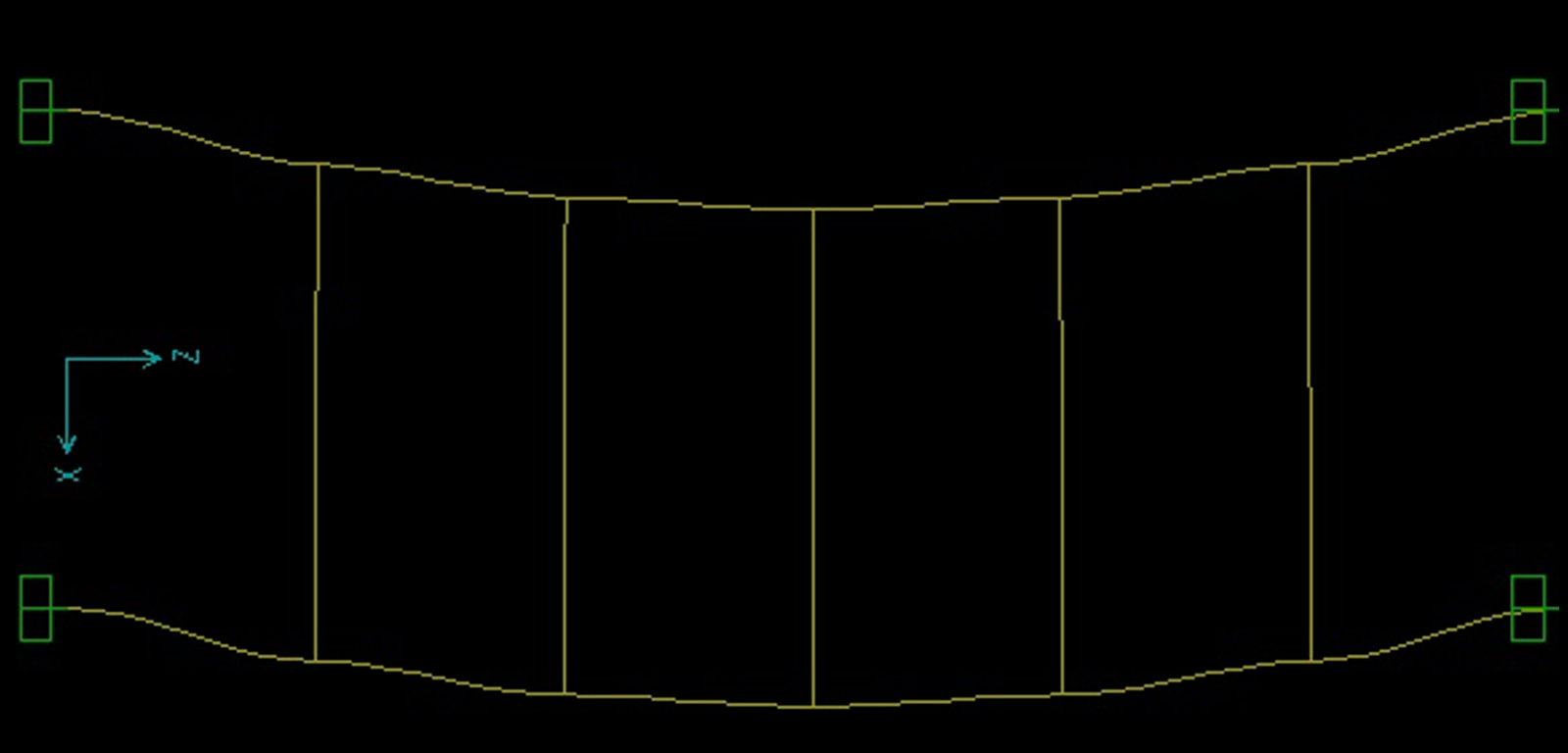
Come fatto in precedenza, verifichiamo i risultati ottenuti attraverso il software SAP. Utilizziamo nuovamente un modello “2D Frames” e impostiamo numero di piani, di campate e lunghezze. Assegniamo sempre ai pilastri il materiale acciaio di default e una sezione di un profilo qualsiasi; per quanto riguarda le travi, invece, ricordiamoci di modificare i parametri giusti al fine di renderle infinitamente rigide da un punto di vista flessionale: teniamo sempre a mente che la rigidezza dipende dal materiale (modulo elastico E), dalla sezione (momento d’inerzia I) e dalla luce (L), quindi scegliamo di assegnare un materiale dal modulo elastico infinitamente elevato. Come possiamo vedere dalle immagini dei diagrammi di Taglio e Momento e dalla deformata i risultati precedentemente calcolati sono in linea con il reale comportamento della struttura: