ESERCITAZIONE IV: Analisi di una trave iperstatica attraverso il Metodo delle Forze

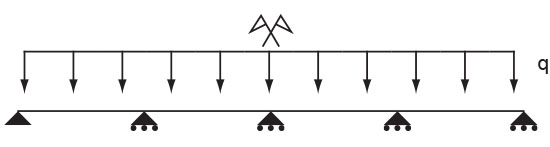
A partire dal precedente schema strutturale iperstatico si vuole ottenere l'andamento di Momento e Taglio per ogni sezione di esso. Partiamo anzitutto riducendo la struttura ad una isostatica sostituendo per ciascun vincolo incognito una forza, intesa come ente dinamico capace di generare spostamento, tale che per l'intorno del punto in cui viene applicata la situazione cinematica rimanga inalterata.

Questo algoritmo prende il nome di Metodo delle Forze.

Si vuole ridurre il grado di vincolo del carrello in modo tale che esso consenta la rotazione relativa delle aste da esso collegate.

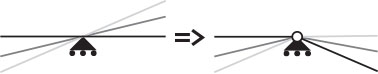
Per ripristinare la continuità sarà necessario dunque applicare un momento tale da ripristinare la continuità:

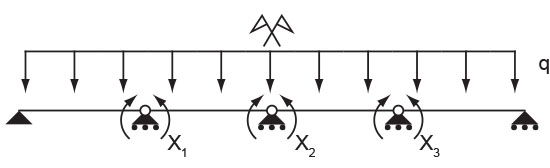
Per porre dei riferimenti sulla trave indichiamo con le seguenti lettere i punti di discontinuità della trave:

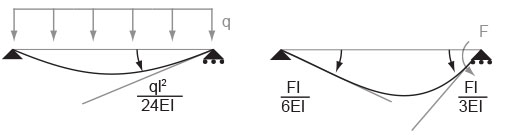
Ricordiamo inoltre i seguenti schemi noti riguardo le rotazioni generate su trave appoggiata rispettivamente da un carico distribuito e da un momento applicato su uno dei carrelli terminali:

Essendo la struttura simmetrica possiamo analizzare la struttura fino al punto C sapendo che Taglio e Momento rispettimente saranno antisimmetrico e simmetrico.

Δφ_B=0 così come Δφ_C=0 inoltre agli estremi di B e C i comportamenti delle sezioni di frontiera saranno diversi quindi vanno studiati e analizzati

φ_Bsx = ql³/24EI - X₁l/3EI, φ_Bdx = -ql³/24EI + X₁l/3EI + X₂l/6EI
φ_Csx = ql³/24EI - X₂l/3EI - X₁l/6EI, φ_Cdx = -ql³/24EI + X₂l/3EI + X₁l/6EI

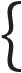ql³²/24EI - X₁l/3EI = -ql³²/24EI + X₁l/3EI + X₂l/6EI
ql³²/24EI - X₂l/3EI - X₁l/6EI = -ql³²/24EI + X₂l/3EI + X₁l/6EI

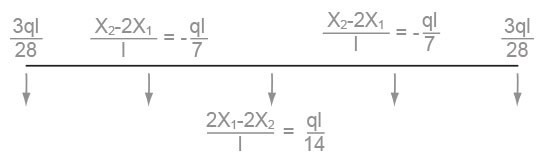
ql²/4 - 2X₁ - X₂/2 = 0
ql²/4 - 2X₂ - X₁ = 0 ⇒ X₁ = ql²/4 - 2X₂

ql²/4 - 2ql²/4 +4X₂ - 2X₂/2  ⇒ X₂ = ql²/14

X₁ = ql²/4 - 2ql²/14 ⇒ X₁ = 7ql²-4ql²/28 ⇒ X₁ = 3ql²/28

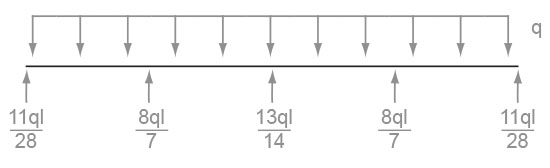
Poniamo in equilibrio le singole aste e quindi ricaviamo l'equilibrio per l'asta isostatica sottoposta a momenti flettenti in A,B,C

+

=

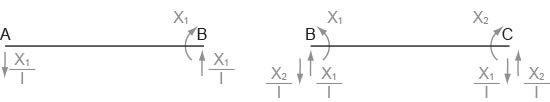
Le funzioni che descrivono il Taglio sono:

T_AB(s) = 11/28ql - qs ⇒ T_AB(l) = -17/28ql
T_BC(s) = -17/28ql + 8/7ql - qs ⇒ T_BC(0) = 15/28ql,  T_BC(l) = 13/28ql

e poichè dM/ds = - T ⇒ M(s) = - ∫T(S) le equazioni del Momento saranno (tenendo conto del valore del momento generato dall'eventuale asta precedente):

M_AB(s) = -11/28qls - qs²/2 ⇒ M_AB(l) = 3/28ql² ,  M_AB(11/28l) = 121/1568ql²
M_AB(s) = -15/28qls - qs²/2 +3/28ql²⇒ M_BC(l) = 1/14ql² ,  M_BC(15/28l) = 57/1568ql²