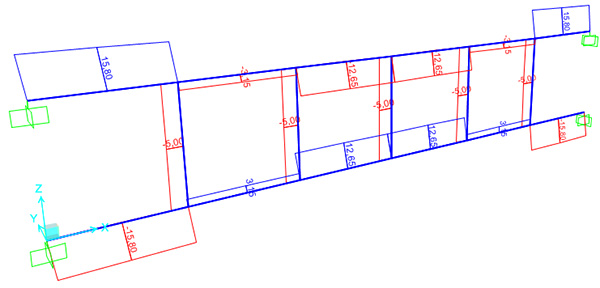
ESERCITAZIONE V: Trave Vieerendel su doppio incastro

Anzitutto si osserva che la trave Vieerendel può essere vista può essere vista come un telaio con travi ShearType le cui proprietà sono note e verificate.

Prima di elencarle è necessario precisare che la risoluzione totale di un telaio ShearType attraverso metodi analitici base può avvenire quando esso si appoggia su due incastri: in questo caso la struttura ha un'ulteriore iperstaticità conferita dal doppio incastro aggiuntivo che come vedremo impedirà la determinazione dello sforzo Normale, in realtà anche a causa del modello stesso che prevede il ritto come infinitamente rigido.

Per via delle sua trave indeformabile lo spostamento in una trave ShearType non può essere diverso da quello rappresentato in figura poichè le travi in generale si ammettono indeformabili assialmente.

La struttura si deforma per assecondare la sua iperstaticità esattamente come una trave doppiamente incastrata sottoposta a cedimento vincolare sull'incastro.

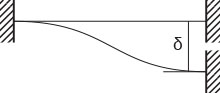
Il cedimento vincolare genera tensioni, figlie in questo caso della forza applicata orizzontalmente.

L'integrazione della linea elastica avviene a partire dall'equazione EIv^IV + q= 0 ma q=0.

φ(s) = 1/2 c₁s² + c₂s + c₃
v(s) = 1/6c₁s³ + 1/2c₂s² + c₃s + c₄

φ(0)=0, φ(l)=0, v(0)=0, v(l)=-δ ⇒ c₁=12/l³ δ , c₁=6/l² δ

χ(s)=φ'(s)= 12/l³ δs - 6/l² δ, M(s)=EIχ=12EI/l³ δs - 6EI/l² δ
⇒ -M'=T ⇒ T(S)=-12EI/l³ δ

F = 2T = 24EI/l³ δ ⇒ δ = Fl³/24EI

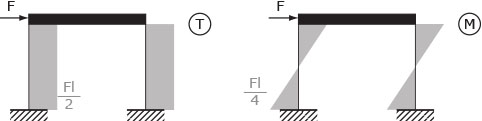
Iterando il modello su un telaio ShearType semplice su due incastri con forze F orizzontali agenti su ogni asta orizzontale si può facilmente verificare che:

- il taglio a partire dall'alto verso il basso per ogni asta verticale è F/2 più tutto il contributo in termini di Forze agente sopra di esso
- il momento è il taglio di quell'asta per la metà del braccio (il pilastro nel telaio ShearType)

Il telaio è stato ruotato a rappresentare una Vieerendel aggettante (il funzionamento è il medesimo)

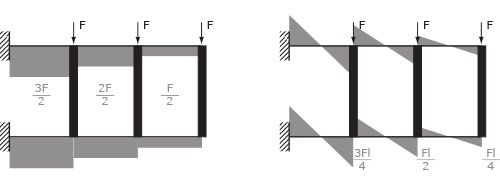
Tornando alla Vieerendel doppiamente appoggiata può essere utile (data la simmetria della struttura) raffigurarla secondo la seguente logica:

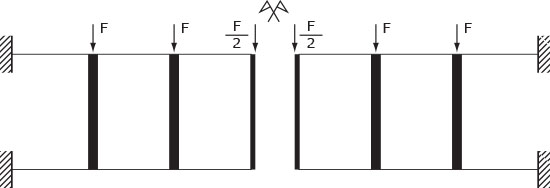
Considerando l e F valori parametrici sostituibili al processo generale illustrato precedentemente (non all'esempio!) facilmente troviamo:

T_CD=F/4 = 12EI/l³ δ ⇒ δ = Fl³/48EI
T_BC=F/4 + F/2 = 3/4 F = 12EI/l³ δ ⇒ δ = 3Fl³/48EI
T_AB=3F/4 + F/2 = 5/4 F = 12EI/l³ δ ⇒ δ = 5Fl³/48EI

Sull'incastro invece per la rigidità dei ritti e la simmetria della struttura la forza totale agente (5/4F) si ripartisce sui 4 incastri.

TAGLIO

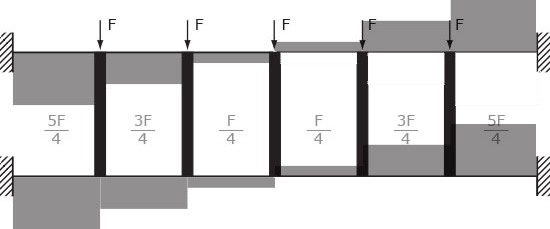
MOMENTO

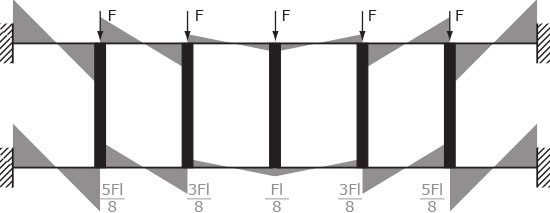
Anche i ritti posseggono un loro equilibrio al momento che è nella fattispecie risolvibile attraverso l'equilibrio nel nodo. Il momento rimane lineare e i picchi, che si hanno nei punti estremi della trave, sono la somma dei valori (tenendo conto dei segni) del momento sulle sezioni di trave orizzontale collegate al nodo.

MOMENTO NEI RITTI

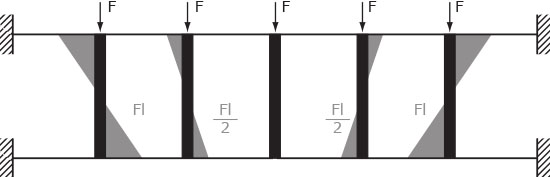
Verifichiamo dunque la validità dei risultati su SAP2000.
Una volta disegnata la struttura assegnamo alle travi e ai ritti sezioni diverse sezioni e al loro incrocio un carico verticale di 10KN con un LoadPatterns con Weight Multiplier = 0.

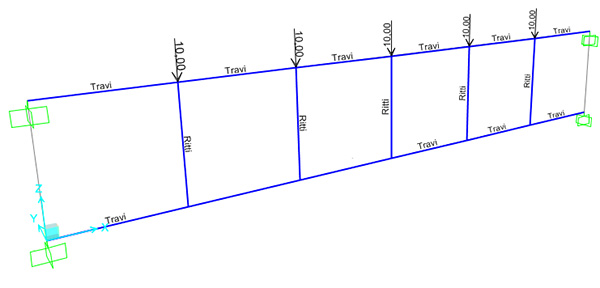
Con sezioni quadrate di 40cm per lato indistintamente dalla sua posizione l'esercizio non sembra essere coerente ai risultati ottenuti. Questo perchè i ritti hanno un fattore EI non sufficiente a rendere quanto più indeformabile la trave.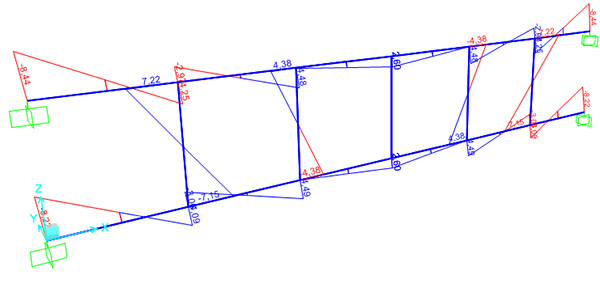

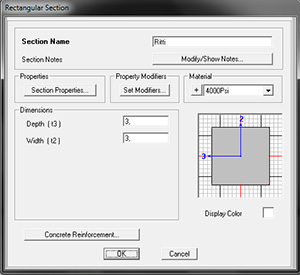
Il modello scelto consente infatti una valutazione bonaria delle azioni di contatto ma lontana dalla realtà. Infatti per avere risultati efficaci (senza modificare le proprietà del materiale) bisogna assegnare una sezione di 3x3m.

Qui di seguito i grafici con le sezioni così assegnate.

TAGLIO

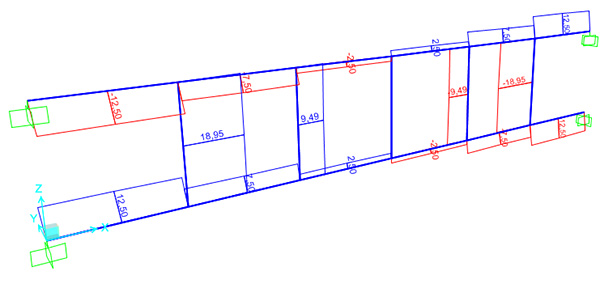
MOMENTO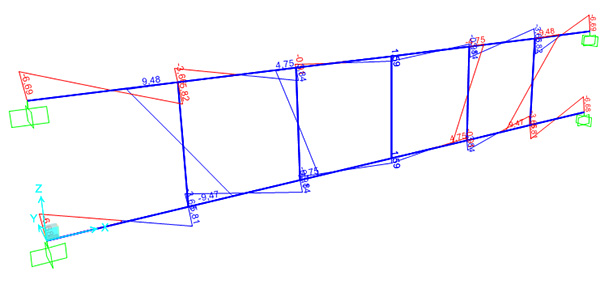

SFORZO NORMALE