esercitazione SISTEMA IPERSTATICO CON METODO DELLE FORZE

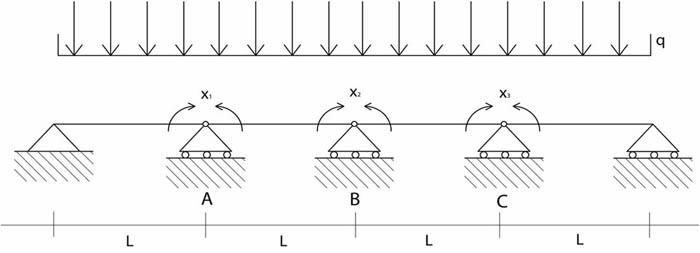
Risolviamo una struttura iperstatica con il metodo delle forze, che consiste nel porre come incognite delle reazioni vincolari, tante quanti sono i gradi di iperstaticità della struttura (nel nostro caso quindi 3). È importante definire bene queste incognite affinchè non rendano labile il sistema della struttura di partenza.

In questo caso le reazioni incognite coincidono con i momenti flettenti, rappresentati come coppie uguali ed opposte, il cui effetto cinematico è quello di evitare la rotazione delle sezioni su cui agiscono, la cui rotazione sarebbe concessa dalle cerniere e precedentemente negata dai vincoli.

Definiamo le equazioni di compatibilità cinematica per ripristinare il vincolo iperstatico

∆ϕB=0   ;     ∆ϕB= ϕBs + ϕBd =0   ;   ϕBs = ϕBd

∆ϕC=0   ;     ∆ϕC= ϕCs + ϕCd =0   ;   ϕCs = ϕCd

∆ϕD=0   ;     ∆ϕD= ϕDs + ϕDd =0   ;   ϕDs = ϕDd

Ora andiamo a studiare le rotazioni nei nodi B e C (è una struttura simmetrica uindi B=D), ponendo i valori noti per una trave appoggiata con un momento applicato a un estremo in modo che mettendole a sistema possiamo ricavare i valori delle incognte X1 e X2

ϕBs = (ql³)24EI  -  (X1l)/3EI

ϕBd = -(ql³)24EI  +  (X1l)/3EI  -  (X2l)/6EI      

ϕCs = (ql³)24EI  -  (X2l)/3EI  -  (X1l)/6EI

ϕCd = -(ql³)24EI  +  (X2l)/3EI  -  (X1l)/6EI      

mettendo le equazioni a sistema otteniamo i valori di X1 e X2 pari a

X1 =( 3ql²)/28               X2=(ql²)/14

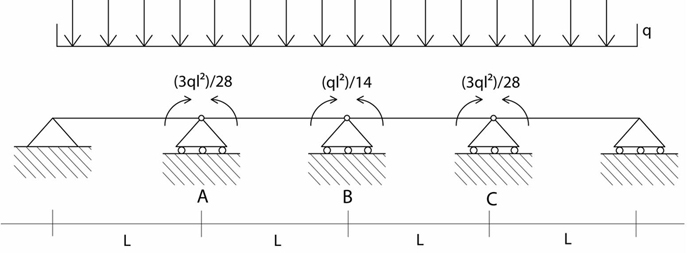
Ora, per applicare il principio di sovrapposizione per trovare il valore delle reazioni semplifichiamo ulteriormente la struttura isostatica in 2 stutture: una dipendente dal carico q e l’altra dipendente dalla reazione vincolare x

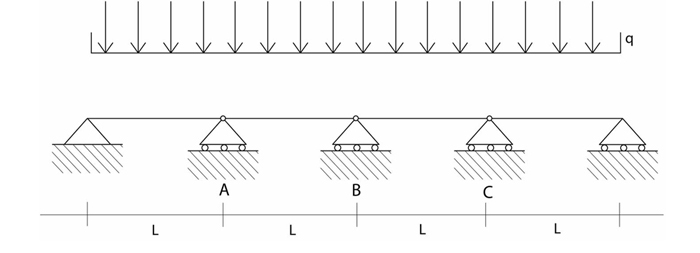
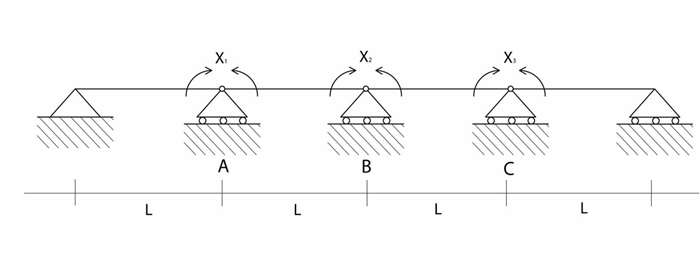
In entrambi i casi possiamo scomporre la struttura in quattro travi reciprocamente incernierate, tutte doppiamente appoggiate sulle quali studieremo le reazioni dipendenti dal carico q e dall’incognita x

Per il carico q

per il momento x

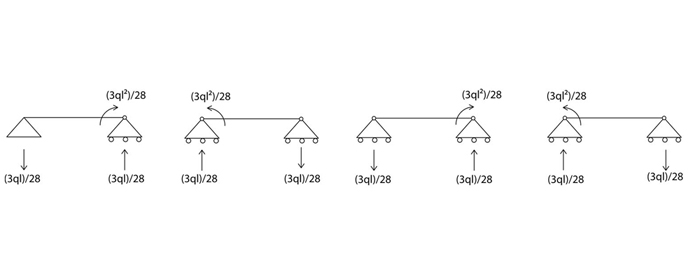
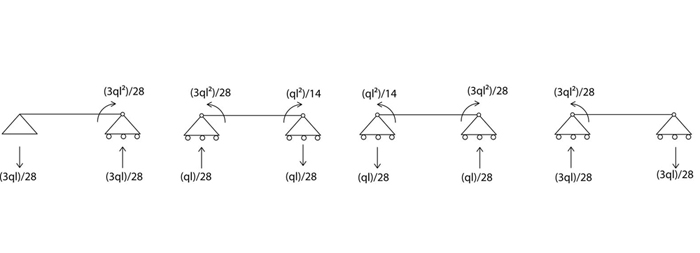
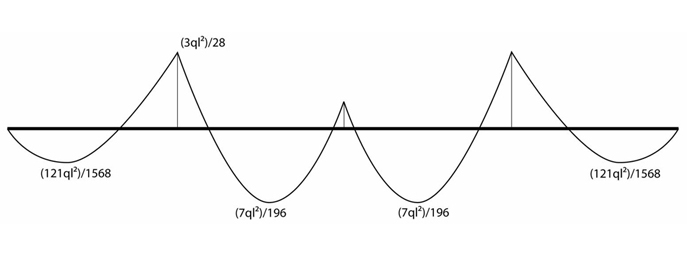
A questo punto possiamo determinare i diagrammi di taglio e momento flettente della struttura iperstatica attraverso l’applicazione del principio di sovrapposizione degli effetti. Quindi andiamo a sovrapporre gli schemi degli effetti dovuti alla densità di carico e alla coppia x per le strutture isostatiche di riferimento.