blog di marta.braconcini

in questa esercitazione studiamo una struttura reticolare tridimenionale con l'ausilio del programma SAP2000, al fine di valutare gli effetti di un carico distribuito su una struttura isostatica di questo tipo. 

la struttura è stata disegnata precedentemete su Rhinoceros per motivi di comodità e poi importata su SAP con il formato .IGS

una volta importato il disegno è bene ridurre la tolleranza di errore del file in modo che, se a seguito dell'importazione, le linee avessero subito qualche variazione come un minimo distanziamento, con il comando MERGE TOLERANCE tutto questo verrebbe evitato e le linee a una distanza inferiore al valore da noi impostato si considererebbero unite

per rendere la stuttura reticolare isostatica assegniamo 3 vincoli a tre nodi inferiori (comandi ASSIGN-JOINT-RESTRAINTS)

assegniamo alle aste una sezione tubolare in acciaio e il peso proprio nullo, in modo che non influenzi l'analisi 

assegniamo un carico distribuito ai nodi superiori pari a 50KN (comandi ASSIGN-JOINT LOADS-FORCES)

avendo a che fare con una trave reticolare in cui i nodi sono cerniere dobbiamo impostare il rilascio dei momenti, un operazione che dichiara l'intrasmissibilità dei momenti attraverso le cerniere.

ora possiamo avviare l'analisi, ottenendo l'immagine accentuata della deformata

da questa analisi possiamo ottenere anche delle tabelle (esportabili su excel) con riportati per esempio i valori delle reazioni vincolari o i valori di taglio e memento per ogni asta che compone la trave, come accade nella tabella riportata sotto.

dato un impalcato di riferimento

con pilasti in acciaio

possiamo individuare 7 telai piani, quattro lungo X e tre lungo Y, composti da due a quattro pilastri ognuno, il cui compito, oltre quello strutturale, è di controventamento per l'intera struttura, cioè sopportare le forze gravanti sul piano X-Y (=orizzontali). 

le molle individuate nella pianta iniziale dell'impalcato stanno a indicare che, se il solaio è pensato rigido nel suo piano, i contronventi sono dotati di una propria elasticità che ci permette di considerarli dei vincoli cedevoli dell'impalcato e quindi di rappresentarli con delle molle con una relativa rigidezza K= (12EI)/h³, in cui I è la sommatria dei momenti di inerzia dei pilastri coinvolti ne telaio di riferimento.

a questo punto, con il foglio exel di calcolo, possiamo iniziare a studiare singolarmente i telai in base alle caratteristiche e al numero dei pilastri che li compongono.

a questo punto possiamo raccogliere i risultati delle rigidezze ottenuti dallo studio dei telai in una tabella sinottica, in cui scriveremo anche i valori delle distanze coordinate dei pilastri dal punto o(0,0), origine degli assi cartesiani. 

il terzo passo di questo algoritmo consiste nel calcolo delle coordinate del centro di massa del nostro impalcato. per fare ciò però bisogna semplificare la pianta a forme basilari, nel nostro caso due rettangoli, dei quali calcoleremo i rispettivi centri.

come si può leggere nell'immagine, le coordinate della prima sezione (da sinistra a destra) sono X=3  Y=18, mentre quelle della seconda sezione  X=9  Y=8, la cui media ponderata in base alle aree delle rispettive sezioni darà come risultato le coordinate del centro di massa dell'intero impalcato.

a questo punto, con le rigidezze orizzontali e verticali totali possiamo calcolare, sempre con il foglio excel, le coordinate del centro delle rigidezze, cioè (in semplici parole) il punto in cui è applicata la risultante delle forze resistenti, e le distanze dei controventi da tale punto.

si nota dai dati ottenuti che le coordinate del centro delle rigidezze coincidono con quelle del centro delle masse ottenuto prima; questo significa che il nostro impalcato è equilibrato e che non subirà rotazione a seguito dell'applicazione di forse orizzontali (come possono essere le forze sismiche)

ora, in base all'area totale dell'impalcato e ai dati dei carichi dati da normativa, otteniamo il valore della forza sismica (forza orizzontale)

sappiamo che questa forza sismica F è ripartita lungo gli assi X e Y, non resta che sapere in che proporzione per ogni telaio atraverso il prodotto tra la rigideza del telaio, la distanza di questo dall'origine e il valore della rotazione dell'impalcato:

asse X

asse Y

Risolviamo una struttura iperstatica con il metodo delle forze, che consiste nel porre come incognite delle reazioni vincolari, tante quanti sono i gradi di iperstaticità della struttura (nel nostro caso quindi 3). È importante definire bene queste incognite affinchè non rendano labile il sistema della struttura di partenza.

In questo caso le reazioni incognite coincidono con i momenti flettenti, rappresentati come coppie uguali ed opposte, il cui effetto cinematico è quello di evitare la rotazione delle sezioni su cui agiscono, la cui rotazione sarebbe concessa dalle cerniere e precedentemente negata dai vincoli.

Definiamo le equazioni di compatibilità cinematica per ripristinare il vincolo iperstatico

∆ϕB=0   ;     ∆ϕB= ϕBs + ϕBd =0   ;   ϕBs = ϕBd

∆ϕC=0   ;     ∆ϕC= ϕCs + ϕCd =0   ;   ϕCs = ϕCd

∆ϕD=0   ;     ∆ϕD= ϕDs + ϕDd =0   ;   ϕDs = ϕDd

Ora andiamo a studiare le rotazioni nei nodi B e C (è una struttura simmetrica uindi B=D), ponendo i valori noti per una trave appoggiata con un momento applicato a un estremo in modo che mettendole a sistema possiamo ricavare i valori delle incognte X1 e X2

ϕBs = (ql³)24EI  -  (X1l)/3EI

ϕBd = -(ql³)24EI  +  (X1l)/3EI  -  (X2l)/6EI      

ϕCs = (ql³)24EI  -  (X2l)/3EI  -  (X1l)/6EI

ϕCd = -(ql³)24EI  +  (X2l)/3EI  -  (X1l)/6EI      

mettendo le equazioni a sistema otteniamo i valori di X1 e X2 pari a

X1 =( 3ql²)/28               X2=(ql²)/14

Ora, per applicare il principio di sovrapposizione per trovare il valore delle reazioni semplifichiamo ulteriormente la struttura isostatica in 2 stutture: una dipendente dal carico q e l’altra dipendente dalla reazione vincolare x

In entrambi i casi possiamo scomporre la struttura in quattro travi reciprocamente incernierate, tutte doppiamente appoggiate sulle quali studieremo le reazioni dipendenti dal carico q e dall’incognita x

Per il carico q

per il momento x

A questo punto possiamo determinare i diagrammi di taglio e momento flettente della struttura iperstatica attraverso l’applicazione del principio di sovrapposizione degli effetti. Quindi andiamo a sovrapporre gli schemi degli effetti dovuti alla densità di carico e alla coppia x per le strutture isostatiche di riferimento.

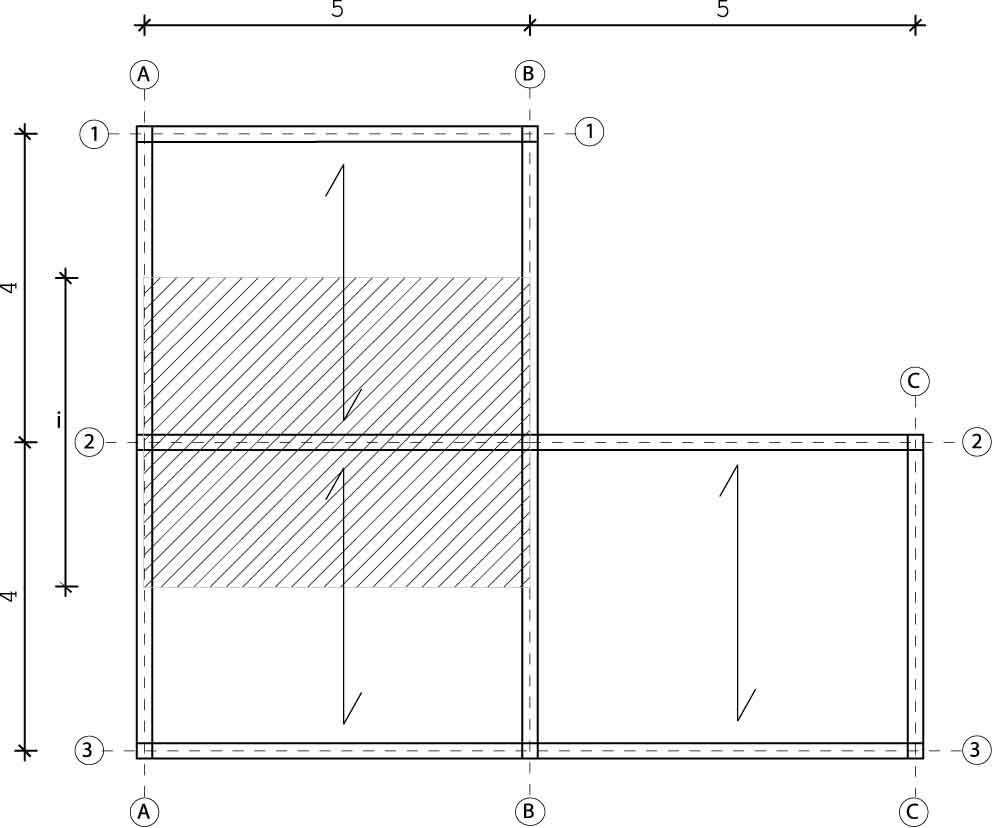
La tecnologia scelta per la struttura di questa pianta a uso residenziale è quella del legno, un materiale leggero perché ricco di acqua e resina e che allo stesso tempo presenta un ottimo rapporto resistenza/peso specifico (= 5KN/m³).                                                                                                                                             Vediamo sul disegno della pianta una zona tratteggiata che evidenzia l’area di influenza  della trave soggetta a maggior sforzo, scelta in base proprio alla misura dell’area di influenza e alla sua lunghezza.

In particolare la scelta è ricaduta sul pioppo, tra i legni “poveri” uno di quelli che rispondono meglio alle necessità strutturali.

Il solaio presenta gli elementi basilari per una struttura del genere, arrivando a uno spessore di 29 cm circa escluso quello della trave che dobbiamo ancora dimensionare.

Nonostante abbiamo a disposizione un foglio excel che può supportare i seguenti calcoli, proviamo a eseguirli ugualmente a mano per poi confrontarli e verificarli con la tabella excel .

Iniziamo con l’analisi dei carichi strutturali, permanenti e accidentali.

-----------------------------------------------------------------------------------------

Carichi strutturali qs, che comprendono il peso degli elementi portanti

Travetti in pioppo

Peso specifico = 5KN/m³

Volume = 0,08 x 0,1 x 1 = 0,008m³

Peso al m² = 5 x 0,08 x 0,1 x 2 = 0,08KN/m²     è moltiplicato per due perchè secondo l’interasse tra i travetti  possiamo dedurre che ogni metro ci sono sicuramente due travetti

Tavolato in pioppo

Peso specifico = 5KN/m³

Volume = 0,035 x 1 x 1 = 0,035m³

Peso al m² = 5 x 0,035 = 0,175KN/m²  

Caldana

Peso specifico = 18KN/

Volume = 0,05 x 1 x 1 = 0,05m³

Peso al m² = 18 x 0,05 = 0,9 KN/m²

Totale qs = 1,15KN/m²

--------------------------------------------------------------------------------

Carichi permanentiqp, cioè quegli elementi di sovraccarico che gravano costantemente, permanentemente sugli elementi strutturali

Pavimento parquet in rovere

Peso specifico = 7KN/m³

Volume = 0,015 x 1 x 1 = 0,015m³

Peso al m² = 7 x 0,015 = 0,1KN/m²  

Massetto in cls alleggerito

Peso specifico = 4,7KN/m³

Volume = 0,04 x 1 x 1 = 0,04m³

Peso al m² = 4,7 x 0,04 = 0,2KN/m²  

Isolamento in fibra di legno

Peso specifico = 2,1KN/m³

Volume = 0,05 x 1 x 1 = 0,05m³

Peso al m² = 2,1 x 0,05 = 0,1KN/m²  

Incidenza impianti = 1KN/m²

Incidenza tramezzi = 1KN/m²

Muro di tamponamento  = 2KN/m²

Totale qp = 4,4 KN/m²

--------------------------------------------------------------------------------

Carichi accidentali qa, cioè quelli dovuti all’uso dell’ambiente. Nel nostro cosa, come abbiamo scritto precedentemente, si tratta di un uso residenziale

Totale qa = 2 KN/m² (da normativa)

--------------------------------------------------------------------------------

TOTALE CARICHI

qs + qp + qa = 1,15 + 4,4 + 2 =7,55KN/m²

--------------------------------------------------------------------------------

Avendo il valore totale dei carichi, ora possiamo calcolare il valore del carico distribuito sulla trave presa in esame, moltiplicando la somma dei carichi per il valore i, cioè l’ampiezza dell’area di influenza degli stessi carichi sulla trave.

Q = (qL²)/2 x i = 7,55 x 4 = 30,2KN/m²

Ora calcoliamo il momento massimo che insiste sulla trave, valutata come una trave appoggiata con un carico distribuito. L è l’altra dimensione dell’area di influenza

abbiamo ottenuto una trave in legno con dimensioni 200x550mm

andiamo a verificare con il foglio excel se i nostri calcoli sono giusti.

i dati calcolati con excel corrispondono a quelli svolti a mano! 

ma cosa succederebbe se considerassimo anche il peso della trave stessa?                                                                          sommiamo ai carichi strutturali quello della trave appena calcolata

Trave in pioppo

Peso specifico = 5KN/m³

Volume = 0,2 x 0,55 x 1 = 0,11m³

Peso al m² = 5 x 0,11 = 0,55KN/m²

Totale qs = 1,15 + 0,55 =1,7 KN/m²

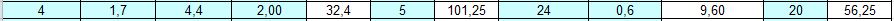
notiamo che l'altezza della trave è cambiata, pertanto le dimensioni sarebbero 200x600mm (arrotondando sempre per eccesso)