esercitazione RIPARTIZIONE FORZA SISMICHE

dato un impalcato di riferimento

con pilasti in acciaio

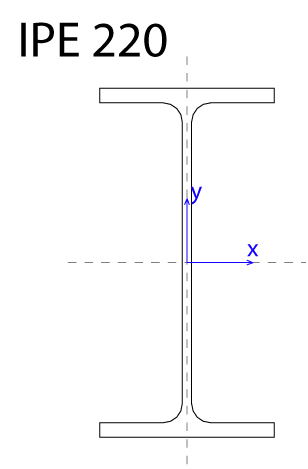
possiamo individuare 7 telai piani, quattro lungo X e tre lungo Y, composti da due a quattro pilastri ognuno, il cui compito, oltre quello strutturale, è di controventamento per l'intera struttura, cioè sopportare le forze gravanti sul piano X-Y (=orizzontali). 

le molle individuate nella pianta iniziale dell'impalcato stanno a indicare che, se il solaio è pensato rigido nel suo piano, i contronventi sono dotati di una propria elasticità che ci permette di considerarli dei vincoli cedevoli dell'impalcato e quindi di rappresentarli con delle molle con una relativa rigidezza K= (12EI)/h³, in cui I è la sommatria dei momenti di inerzia dei pilastri coinvolti ne telaio di riferimento.

a questo punto, con il foglio exel di calcolo, possiamo iniziare a studiare singolarmente i telai in base alle caratteristiche e al numero dei pilastri che li compongono.

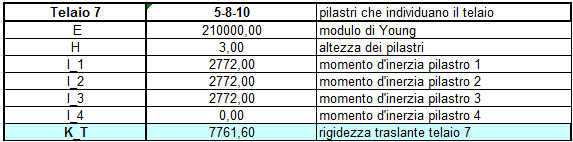
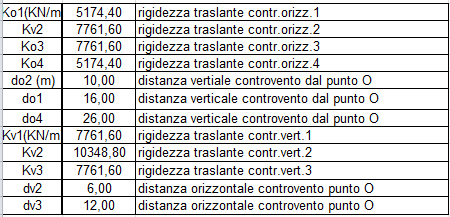
a questo punto possiamo raccogliere i risultati delle rigidezze ottenuti dallo studio dei telai in una tabella sinottica, in cui scriveremo anche i valori delle distanze coordinate dei pilastri dal punto o(0,0), origine degli assi cartesiani. 

il terzo passo di questo algoritmo consiste nel calcolo delle coordinate del centro di massa del nostro impalcato. per fare ciò però bisogna semplificare la pianta a forme basilari, nel nostro caso due rettangoli, dei quali calcoleremo i rispettivi centri.

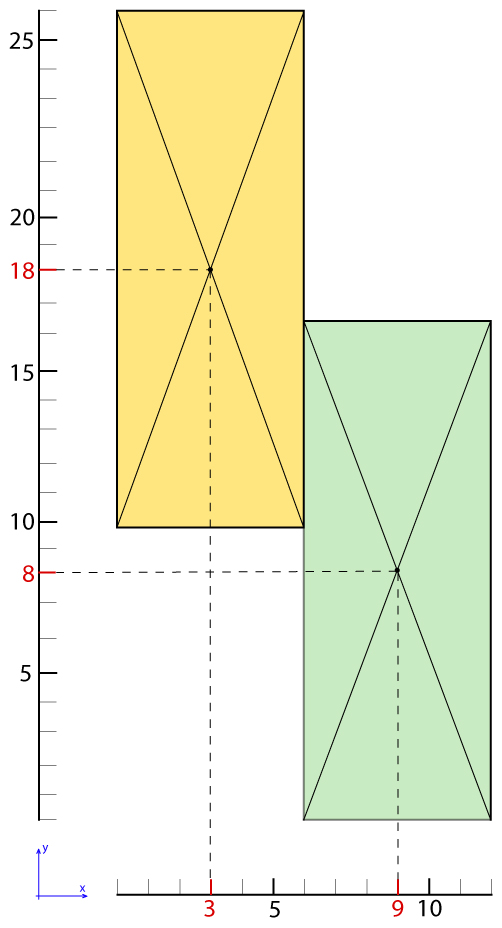
come si può leggere nell'immagine, le coordinate della prima sezione (da sinistra a destra) sono X=3  Y=18, mentre quelle della seconda sezione  X=9  Y=8, la cui media ponderata in base alle aree delle rispettive sezioni darà come risultato le coordinate del centro di massa dell'intero impalcato.

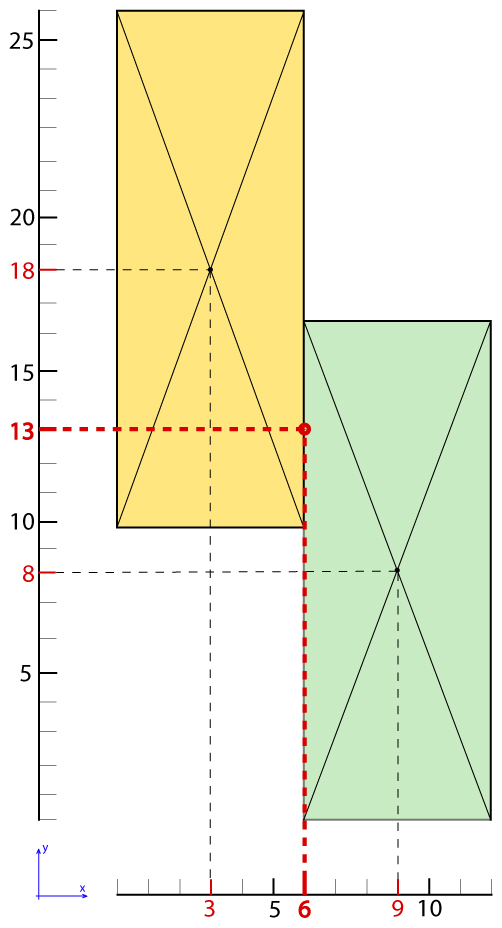
a questo punto, con le rigidezze orizzontali e verticali totali possiamo calcolare, sempre con il foglio excel, le coordinate del centro delle rigidezze, cioè (in semplici parole) il punto in cui è applicata la risultante delle forze resistenti, e le distanze dei controventi da tale punto.

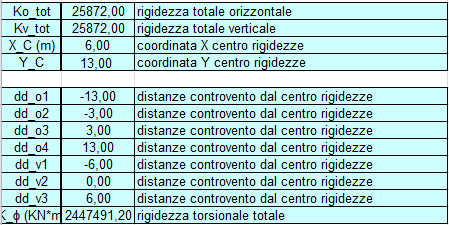
si nota dai dati ottenuti che le coordinate del centro delle rigidezze coincidono con quelle del centro delle masse ottenuto prima; questo significa che il nostro impalcato è equilibrato e che non subirà rotazione a seguito dell'applicazione di forse orizzontali (come possono essere le forze sismiche)

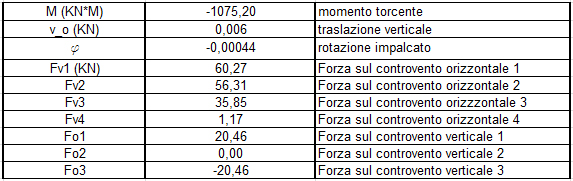
ora, in base all'area totale dell'impalcato e ai dati dei carichi dati da normativa, otteniamo il valore della forza sismica (forza orizzontale)

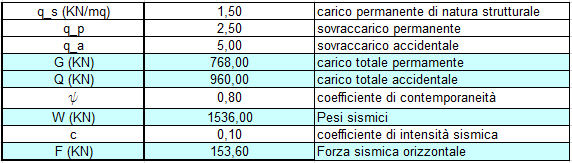
sappiamo che questa forza sismica F è ripartita lungo gli assi X e Y, non resta che sapere in che proporzione per ogni telaio atraverso il prodotto tra la rigideza del telaio, la distanza di questo dall'origine e il valore della rotazione dell'impalcato:

asse X

asse Y