Facoltà di Architettura - Università degli Studi Roma Tre
Es5_Rigidezza e metodo
Un portale è una struttura che va guardata nel suo complesso, in quanto il suo comportamento è sistematico.
Nel caso che segue la struttura è una volta iperstatica e il nostro obiettivo è quello di trovare la rigidezza del
telaio, cioè il coefficiente che lega F a δ.
Prendo una struttura isostatica di riferimento e risolvo il sistema con il metodo delle forze.
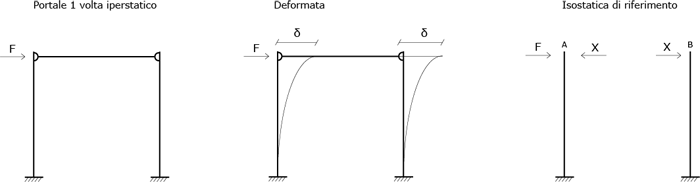
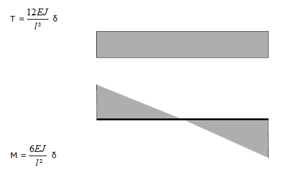
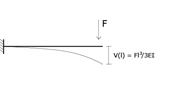
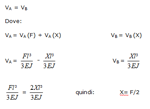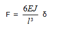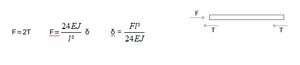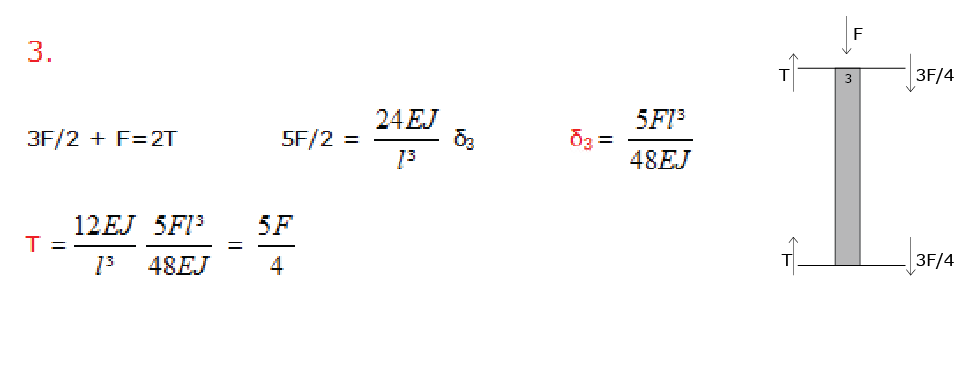Per quanto riguardo gli spostamenti dei punti A e B posso identificare i due pilastri come due mensole con forza
concentrata all’estremo libero. Quindi:
Equazione di compatibilità cinematica
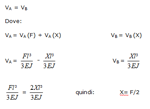
Dal sistema finale risulterà che la forza iniziale F influisce sia sul primo che sul secondo pilastro
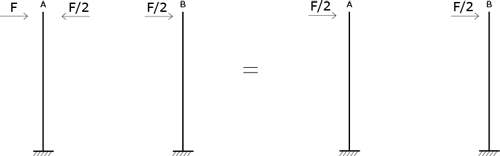
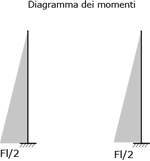
Quindi lo spostamento finale δ è pari a quello di una mensola con una forza F/2 all’estremità
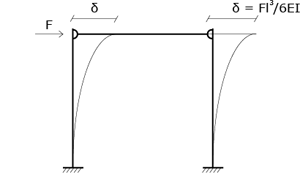
Dove la rigidezza, il coefficiente che lega F a δ,è pari a:
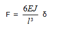
Se considero sistemi più complessi come quello in figura, avrò un comportamento strutturale (sistematico)
in cui la forza F sarà ripartita in ogni pilastro in modo uguale
Telaio shear-type
Diverso è il caso del telaio shear-type, costituito da una trave che si presenta come un elemento pieno, un corpo
infinitamente rigido, e due pilastri flessibili. L’unica deformazione possibile per questo tipo di telaio è la seguente,
in quanto la forza sposta la trave in maniera rigida e trascina con sé i pilastri che si flettono.
Per conoscere in questo caso quanto vale la rigidezza del sistema, considero una situazione analoga: la mensola
incastra ai due estremi. Suppongo che uno dei due incastri ceda, provocando una deformazione e quindi una curvatura.
In questo caso il taglio vale 0, quindi il momento è lineare. Il punto in cui il momento è nullo e quindi anche la curvatura
è nulla (M=EJχ), è detto punto di flesso.
Per sapere quanto vale il momento risolvo la struttura iperstatica con il metodo della linea elastica, e otterrò i seguenti
valori di taglio e momento:
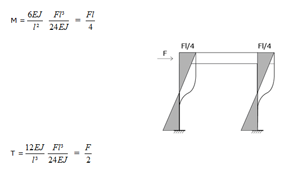
A questo punto torno al sistema iniziale del telaio shear-type e lo risolvo utilizzando il metodo delle rigidezze, che mi
permetterà di conoscere il valore dello spostamento δ provocato da F.
Scrivo l’equazione di equilibrio provocata da F:
Sostituendo δ posso conoscere i valori di M e T e introduco così la rigidezza:
Esempio di telaio a più piani
ESERCIZIO TRAVE VIERENDEEL_1
Una trave Vierendeel può essere vista come un sistema shear-type ribaltato. Quindi anche qui sono presenti degli
elementi infinitamente rigidi ed elementi flessibili.
Risolvo la struttura utilizzando il metodo delle rigidezze, che mi permetterà di calcolare i valori degli spostamenti δe di
verificare i valori del taglio.
Ora conosco tutti i valori del taglio negli elementi orizzontali.
- Diagramma T
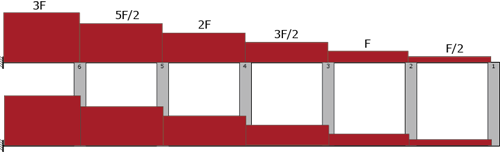
Per conoscere i valori dei momenti sugli elementi orizzontali, basterà moltiplicare la forza di taglio per il suo braccio l/2.
- Diagramma M
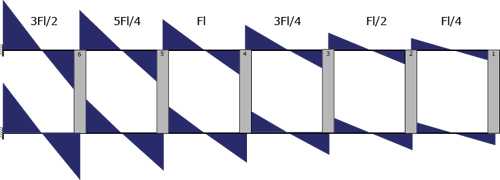
Per conoscere i valori del momento su ogni elemento verticale, calcolo l’equilibrio in ogni nodo.
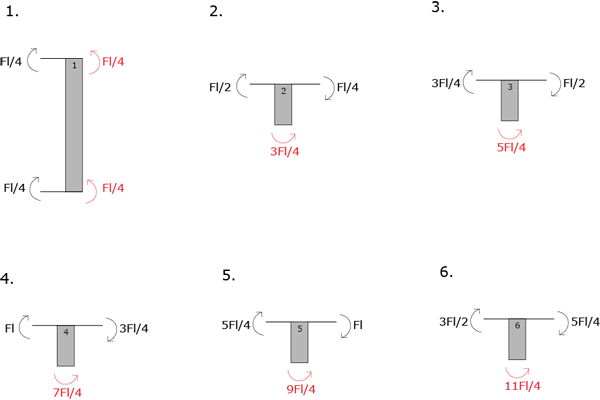
Ora posso fare l’equilibrio di ogni elemento verticale per sapere il valore del taglio.
- Diagramma T
- Diagramma M
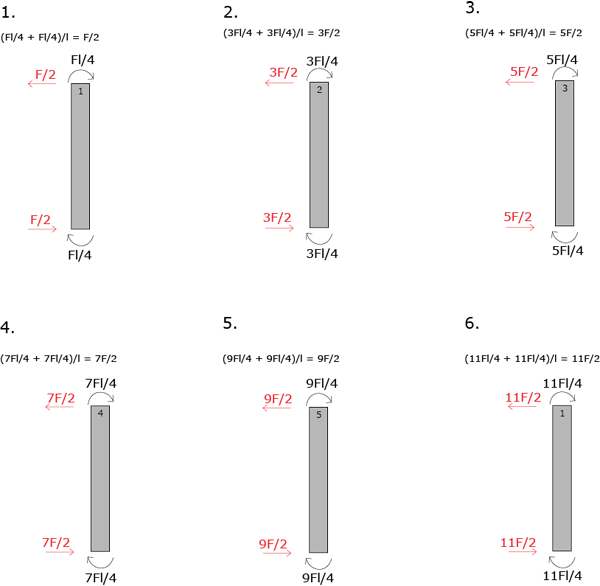
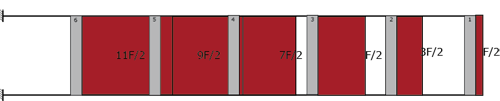
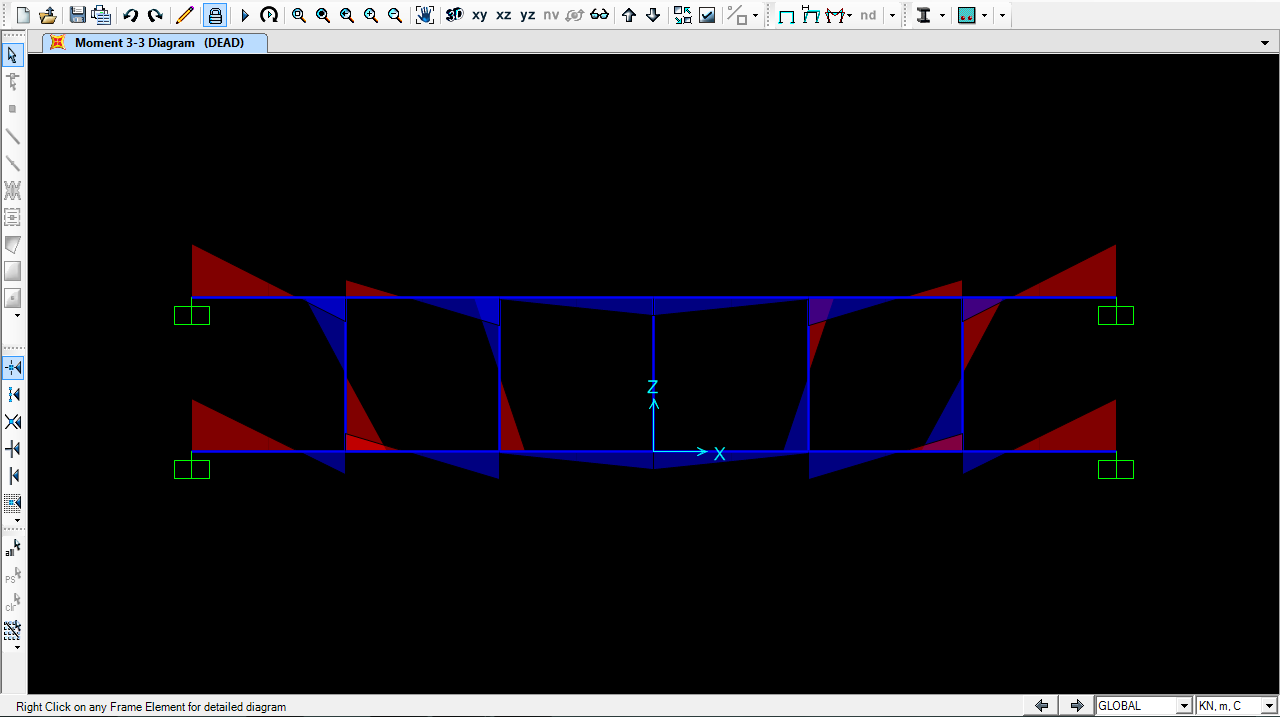
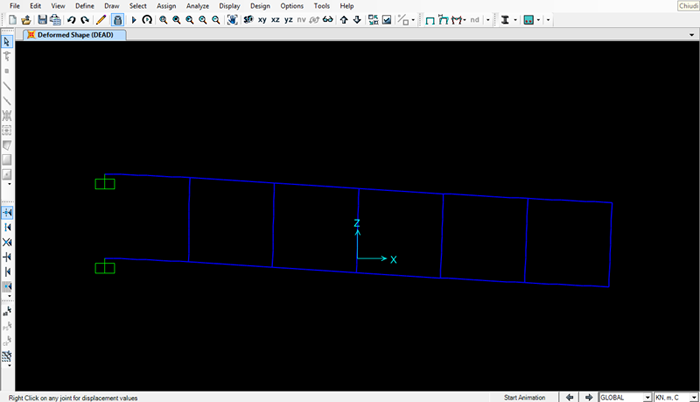
Ora verifico i valori su SAP2000
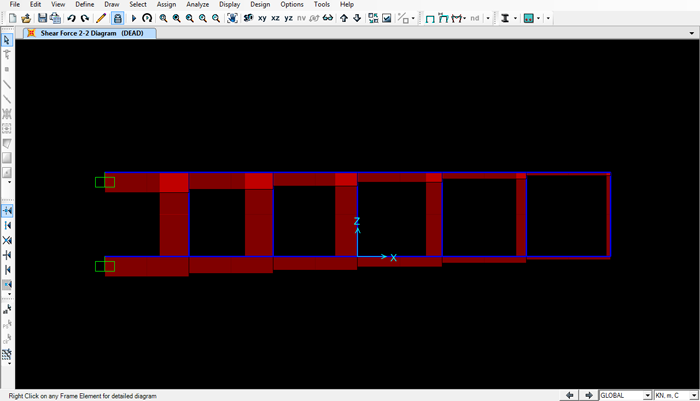
Deformata
Taglio
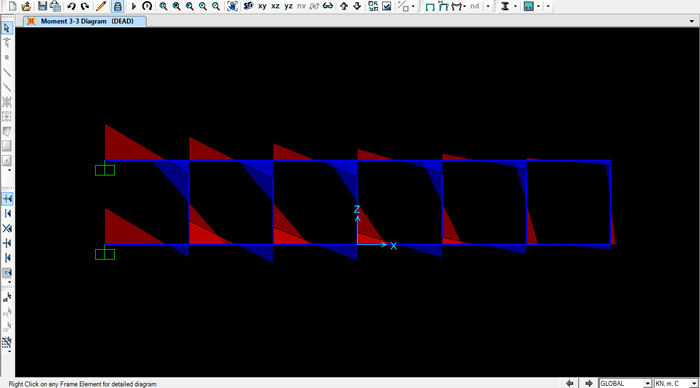
Momento
ESERCIZIO TRAVE VIERENDEEL_2
In questo caso la struttura è incastrata su entrambi i lati.
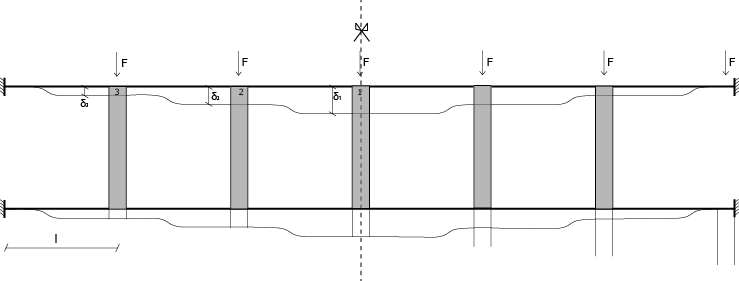
Posso vederla come una struttura simmetrica, quindi vado ad analizzare la parte sinistra della utilizzando sempre il
metodo delle rigidezze.
Intuitivamente i valori del taglio nel pilastro centrale valgono F/4, ma andrò comunque a verificarlo calcolando anche
lo spostamento δ di ogni elemento.
Ora conosco tutti i valori del taglio negli elementi orizzontali.
Diagramma T
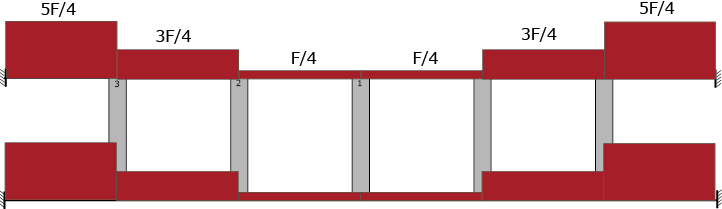
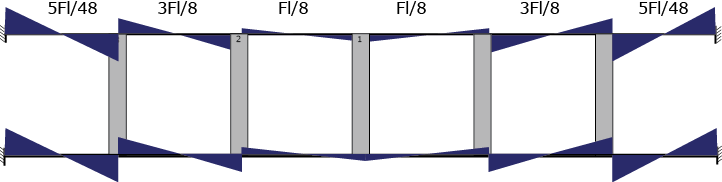
Per conoscere i valori dei momenti sugli elementi orizzontali, basterà moltiplicare la forza di taglio per il suo braccio l/2.
Diagramma M
Per conoscere i valori del momento su ogni elemento verticale, calcolo l’equilibrio in ogni nodo.
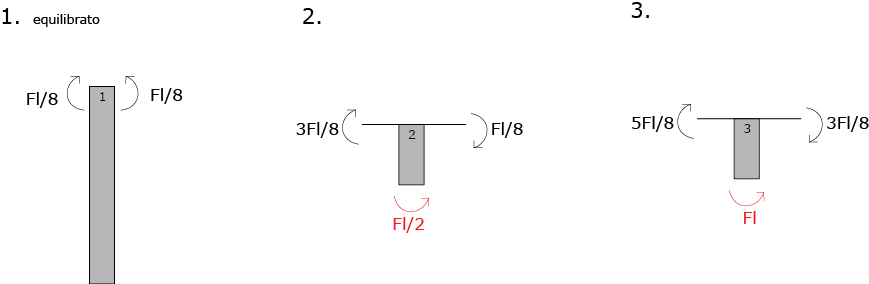
Ora posso fare l’equilibrio di ogni elemento verticale per sapere il valore del taglio.
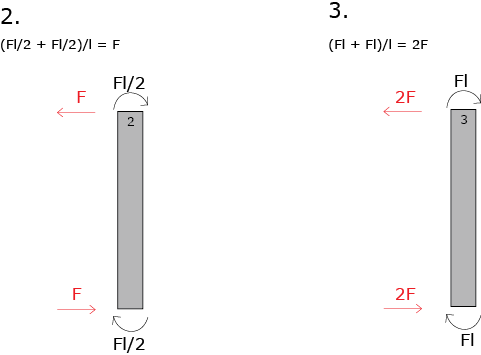
Diagramma T
Diagramma M
Ora verifico i valori su SAP2000
Deformata
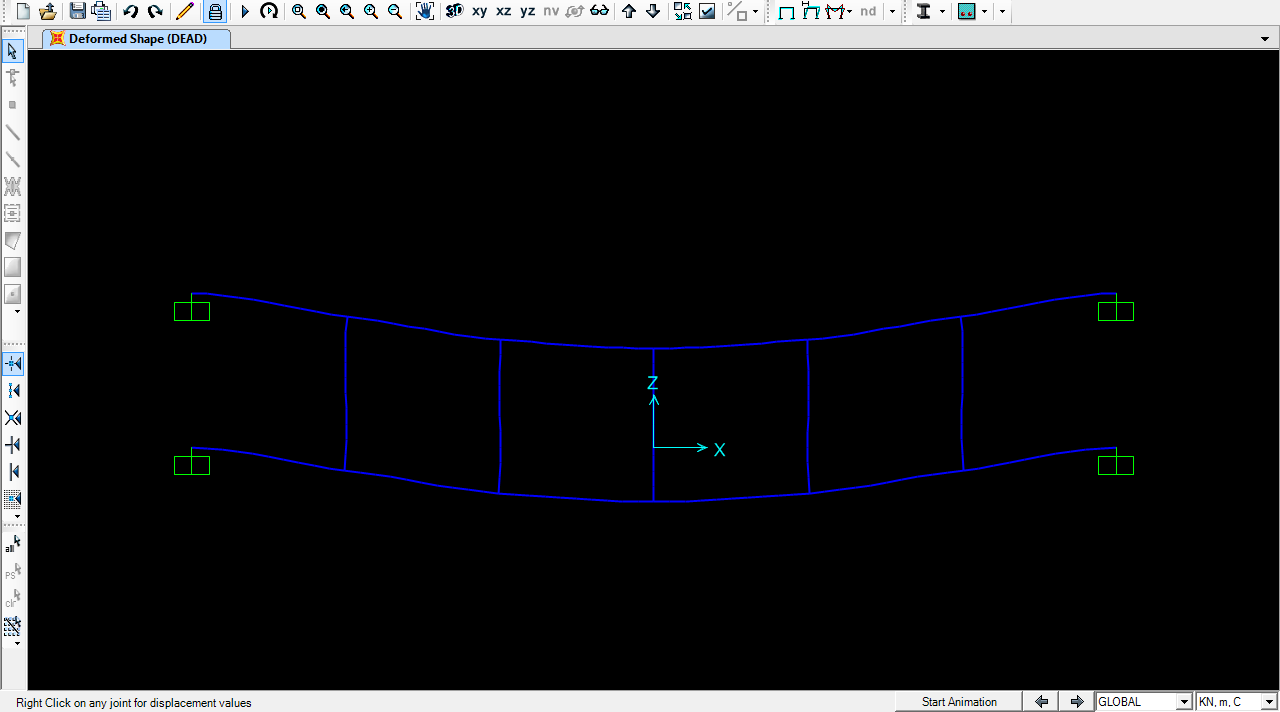
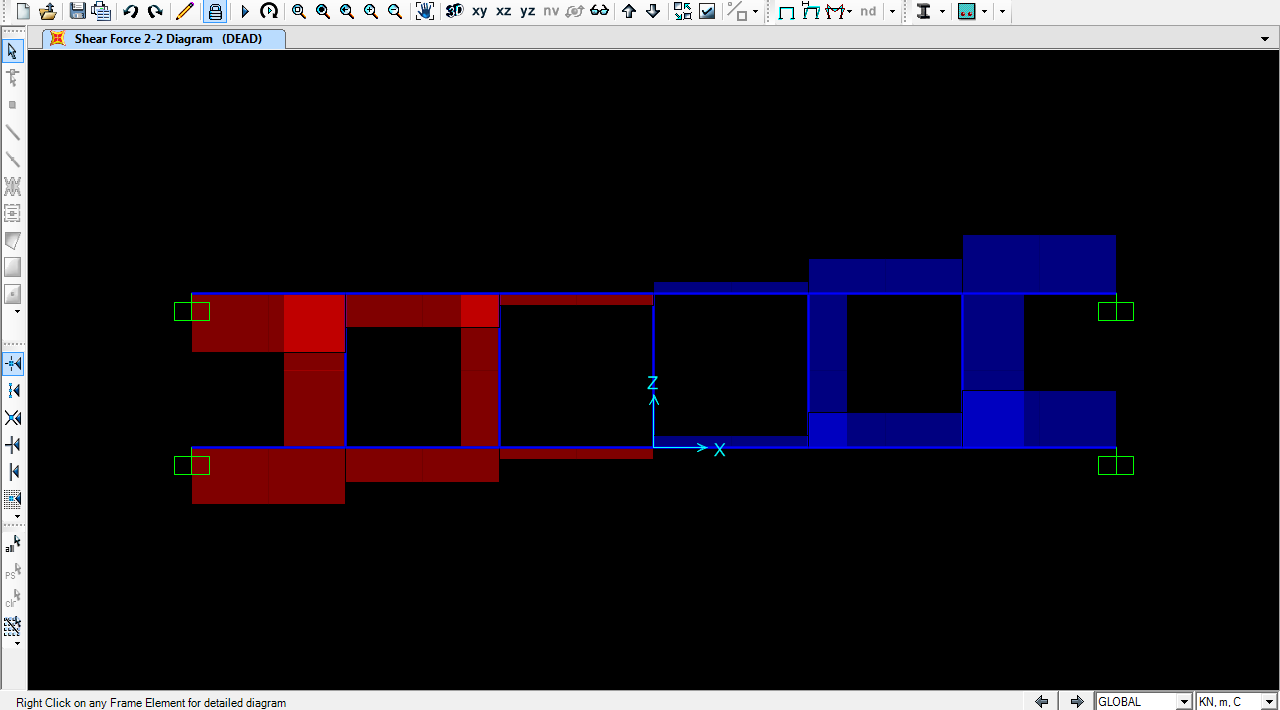
Taglio
Momento
