Esercitazione 5 - Risoluzione di una trave Virendeel doppiamente incastrata mediante il metodo delle rigidezze

RISOLUZIONE DI UNA TRAVE VIERENDEEL MEDIANTE IL METODO DELLE RIGIDEZZE

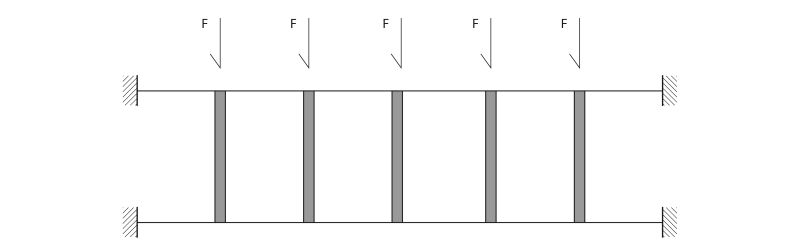
Una trave Vierendeel è una somma di telai Shear Type, che sono strutturati in questo modo:

Gli elementi verticali sono incastrati a terra e la trave (che per definizione è indeformabile) è incastrata ai pilastri. L'insieme di questi elementi può essere considerato come telaio piano. Questo sistema ha un comportamento meccanico che gli consente di fare a meno di controventi, la resistenza ai carichi orizzontali (vento o sismi) è affidata ai pilastri, o meglio alla loro rigidezza.

Per evidenziarne i punti di forza di questo schema strutturale è utile confrontarlo con il portale con l'elemento di collegamento incernierato alla sommità dei pilastri.

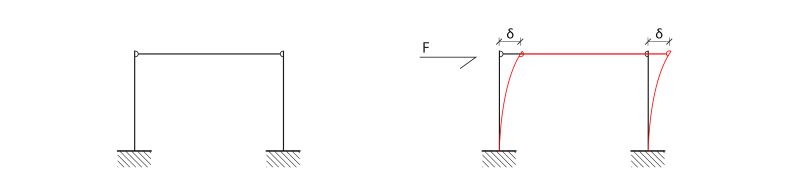
In questo caso la rotazione dei pilastri non è in nessun modo vincolata nella parte sommitale, e tutto il momento flettente si concentra alla base dei pilastri, in corrispondenza dei vincoli. Sovrapponendo più telai di questo tipo (come nel caso di un edificio multipiano) e verificandone il comportamento meccanico all'applicazione di forze orizzontali si evidenzia come il momento si trasmette da piano a piano, crescendo esponenzialmente e scaricandosi nelle fondazioni. L'esempio, oltre a suggerire che questo tipo di portale non è adatto per strutture multipiano in zona sismica, mette in luce il comportamento sistemico delle strutture formate da più elementi.

Anche nel caso del portale con trave incastrata il momento cresce man mano che ci si avvicina alle fondazioni, ma la presenza delle travi infinitamente rigide, incidendo fortemente sulla deformata dei pilastri per via del vincolo che le collega ad essi, interrompe la continuità del momento provocando un comportamento diverso da quello del telaio precedentemente descritto. A parità di piani, di carichi applicati e di proporzioni della struttura adottando questo tipo di schema strutturale il momento che giunge alle fondazioni è nettamente inferiore rispetto al caso precedente, nonostante la rigidezza dei pilastri sia analoga.

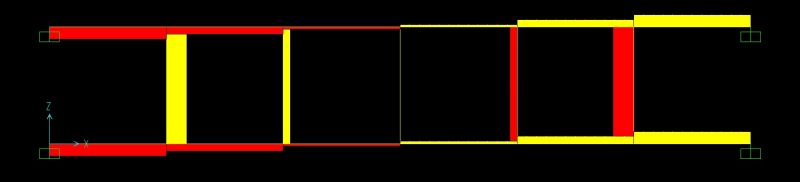
La trave Vierendeel dell'esercizio è doppiamente incastrata. La deformazione del singolo portale sottoposto a un carico perpendicolare ai pilastri è qualitativamente così:

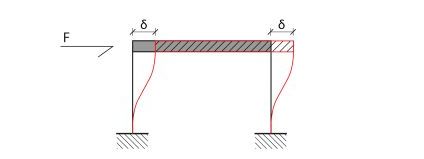
La trave è per definizione infinitamente rigida, di conseguenza non può che traslare o ruotare. I pilastri presentano solo deformazioni flessionali e non assiali. La forza F si ripartisce egualmente nei pilastri che presentano un taglio costante pari a F/2, che è scaricato negli incastri come reazione vincolare.

La trave è incastrata ai 2 pilastri e quindi trasla senza ruotare dato che essi hanno la stessa rigidezza e sono per definizione indeformabili assialmente, quindi presentano la stessa deformata flessionale. Essa è determinata dalle loro condizioni di vincolo: essendo doppiamente incastrati non possono ruotare agli estremi, la parte superiore presenta una traslazione δ, la cui entità è inversamente proporzionale alla rigidità dei pilastri.

Note queste informazioni è facile prevedere il comportamento sistemico della trave Vierendeel doppiamente incastrata. Ogni portale presenta un abbassamento δ, che in termini relativi sarà maggiore in corrispondenza dei vincoli e minore al centro della campata.

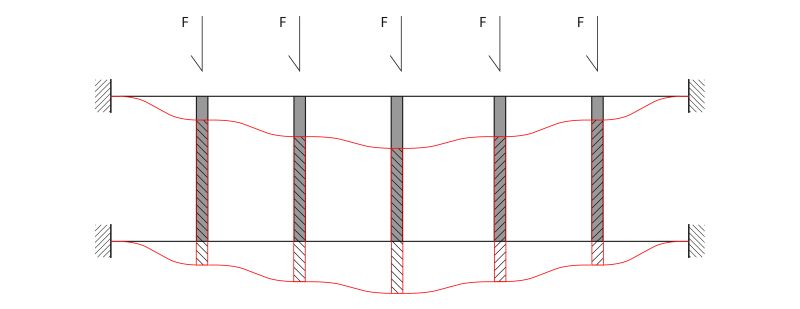
Considerata la simmetria di carichi, vincoli e struttura si può affermare che la deformata stessa sarà simmetrica, con l'asse di simmetria verticale al centro del sistema. Il comportamento del lato opposto a quello analizzato sarà anch'esso simmetrico.

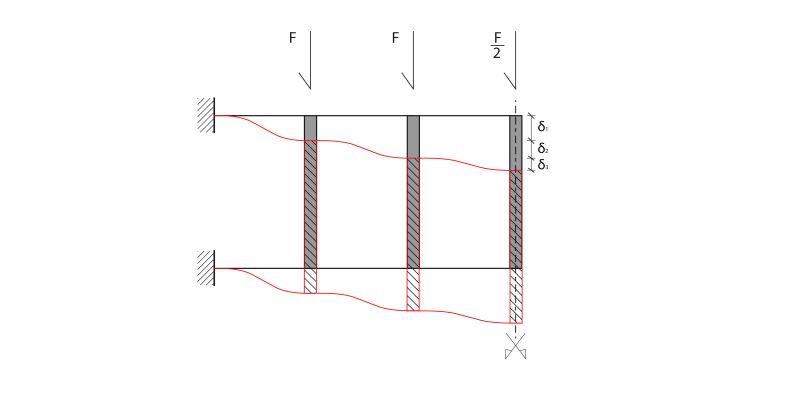
Procedendo a partire dal telaio più lontano dagli incastri si ricava facilmente il taglio nelle travi (gli elementi orizzontali), che cresce di telaio in telaio (aumentando i carichi che si trasmettono attraverso di essi per giungere al vincolo).

Altrettanto semplice è determinare il momento flettente nelle travi, che si ottiene moltiplicando il taglio (che in ogni portale ha andamento costante) per L/2. Esso avrà andamento lineare, sarà zero al centro delle travi, dove la deformata presenta un flesso (dove la curvatura e di conseguenza il momento sono nulli).

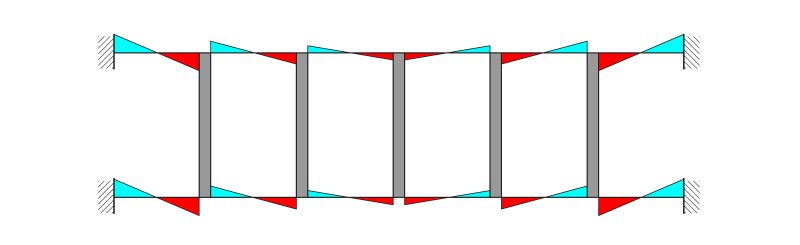
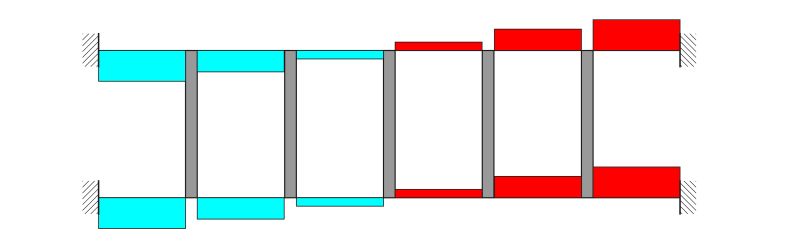
Il momento flettente dei pilastri è ricavato mediante l'equilibrio dei momenti in ogni singolo nodo, dovendo il momento del pilastro bilanciare i 2 momenti concordi dei pilastri che nel suo estremo si incontrano.

Ovviamente la presenza di momento nei pilastri presuppone che ci sia anche il taglio. Esso viene ricavato altrettanto facilmente sommando i momenti agenti sulle travi che sono collegati al pilastro in questione e dividendoli per la lunghezza dello stesso.

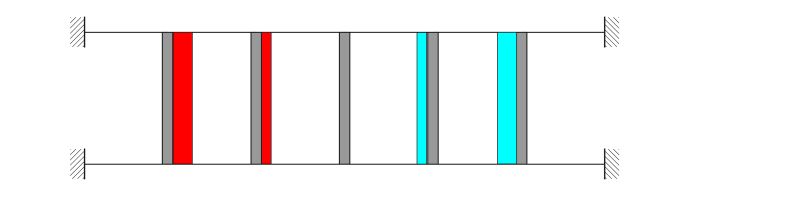
Analizzando esclusivamente metà struttura il pilastro centrale risulterebbe essere sollecitato sia a taglio che a momento flettente, ma per il principio di sovrapposizione degli effetti quando esplicita la simmetria rappresentando la struttura per intero le sollecitazioni di quell'elemento strutturale sono opposte come in ogni pilastro e il suo corrispettivo simmetrico, con la differenza che in questo caso ci si trova proprio sull'asse di simmetria. Per questo le sollecitazioni si annullano, facendo risultare l'elemento scarico.

La verifica su SAP si mette in pratica modellando la struttura partendo da una semplice grid, l'accortezza sta nell'assegnare le sezioni corrette agli elementi strutturali: i pilastri infatti devono essere infinitamente rigidi, di conseguenza ad essi è stata associata una sezione composta da un materiale a cui è stato notevolmente aumentato il modulo di Young, rendendo infinitesime così le deformazioni anche in presenza di tensioni molto alte. 

Usando carichi più pesanti è stata riscontrata una rotazione dei pilastri, incoerente con il modello di telaio Shear Type precedentemente descritto. Questa rotazione è data dal fatto che in sap non è stata inserita la condizione di indeformabilità assiale delle travi.

Questi sono i diagrammi delle sollecitazioni risultato delle analisi, qualitativamente coerenti con quelli ottenuti mediante il calcolo manuale.