commenti

Correzione tavola 6

2 anni 1 settimana fa
diagrammi graticcio

5 anni 9 mesi fa
ultima domanda

5 anni 9 mesi fa
no ho ancora un'ultima

5 anni 9 mesi fa
sì sì tutto chiaro.

5 anni 9 mesi fa

Commenti recenti

Correzione tavola 6 2 anni 1 settimana fa
diagrammi graticcio 5 anni 9 mesi fa
ultima domanda 5 anni 9 mesi fa
no ho ancora un'ultima 5 anni 9 mesi fa
sì sì tutto chiaro. 5 anni 9 mesi fa
Load Pattern peso proprio 5 anni 9 mesi fa
Ciao Fabiana, 5 anni 10 mesi fa
Ciao Giuliana, 5 anni 10 mesi fa
Modellazione setto - Giuliana Nardi 5 anni 10 mesi fa
assegnare sezione a setti su sap 5 anni 10 mesi fa

ESERCITAZIONE 5_SHEAR TYPE E TRAVE VIRENDEEL

Inviato da lorenzo.procaccini il Mer, 08/05/2013 - 23:46

Possiamo indicare come RIGIDEZZA (K) il rapporto tra la FORZA (F) necessaria per imprimere uno spostamento e lo SPOSTAMENTO (δ).

F = k x δ

TELAIO SHEAR TYPE

Con questo modello possiamo indicare uno dei due comportamenti limite di un portale. La caratteristica principale di tale modello è che la trave viene considerata come un CORPO RIGIDO ovvero indeformabile. Questo permette negli incastri (tra trave e pilastro) di avere solo uno spostamento orizzontale (δ) della trave poiché gli unici elementi deformabili sono i pilastri. Come abbiamo accennato precedentemente una volta nota F lo spostamento dipende dalla rigidezza dei pilastri.

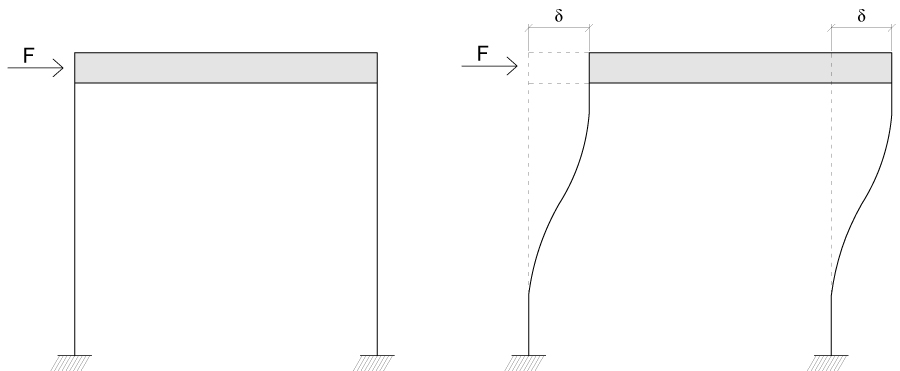
Analizzando i pilastri li possiamo osservare come una struttura 3 volte iperstatica (essendo doppiamente incastrato). Dobbiamo quindi imporre un CEDIMENTO a ridosso della trave ottenendo di conseguenza una DEFORMATA.

Passando all’INTEGRAZIONE DELLA LINEA ELASTICA abbiamo:

$EI\frac{dv^{4}}{ds}+q=0$ in assenza di carico si ha perciò $\frac{dv^{4}}{ds}=0$

$v\left ( s \right )=\frac{C_{1}s^{3}}{6}+\frac{C_{2}s^{2}}{2}+C_{3}s+C_{4}$

$\varphi \left ( s \right )=\frac{C_{1}s^{2}}{2}+C_{2}s+C_{3}$

Dalle CONDIZIONI AL BORDO sappiamo che:

$v\left ( 0 \right )=0\rightarrow C_{4}=0$ $\varphi \left ( 0 \right )=0\rightarrow C_{3}=0$

$v\left ( l \right )=-\delta \rightarrow C_{2}=-\frac{6}{l^{2}}\delta$ $\varphi \left ( l \right )=0\rightarrow C_{1}=\frac{12}{l^{3}}\delta$

Ottenute le equazioni dello SPOSTAMENTO v e della ROTAZIONE φ, derivando quest’ultima ricaviamo la CURVATURA χe di conseguenza il MOMENTO FLETTENTE ed il TAGLIO.

$v\left ( s \right )=\frac{12}{l^{3}}\delta \frac{s^{2}}{6}-\frac{6}{l^{2}}\delta$ $\varphi \left ( s \right )=\frac{12}{l^{3}}\delta \frac{s^{2}}{2}-\frac{6}{l^{2}}\delta s$

$\chi \left ( s \right )=\frac{12}{l^{3}}\delta s-\frac{6}{l^{2}}\delta$ $M\left ( s \right )=EI\chi \left ( s \right )=\frac{12EI}{l^{3}}\delta s-\frac{6EI}{l^{2}}\delta$ $T\left ( s \right )=-\frac{dM}{ds}=-\frac{12EI}{l^{3}}\delta$

Possiamo ora diagrammare i due sforzi: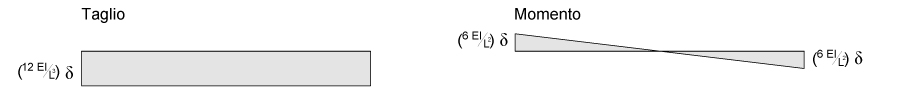

Ovviamente le REAZIONI VINCOLARI ottenute si trasmettono dal PILASTRO alla TRAVE.

Facendo ora l’EQUILIBRIO ALLA TRASLAZIONE della trave possiamo ottenere il valore di δ.

$F=2T=\frac{24EI}{l^{3}}\delta \rightarrow \delta =\frac{Fl^{3}}{24EI}$

Di conseguenza la rigidezza complessiva è paria a:

$k=\frac{24EI}{l^{3}}$

TRAVE VIRENDEEL A MENSOLA

La TRAVE VIRENDEEL è costituita dalla sovrapposizione di più TEALI SHEAR TYPE e quindi possiamo ricorrere al modello precedentemente studiato per poterla analizzare.

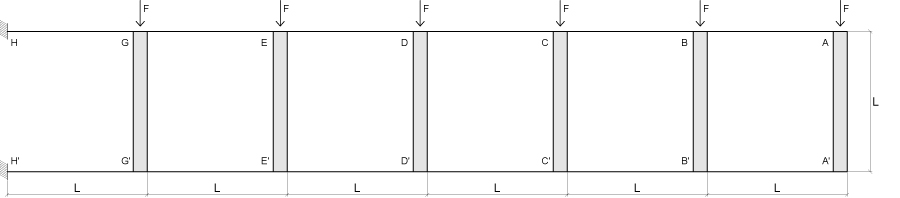
In questo esercizio la Virendeel è disposta come una mensola ed composta da 6 telai. Il vantaggio di utilizzare la trave Virendeel è che per ogni campata il momento flettente deve essere pari 0 al centro e questo permette di avere valori minori nelle reazioni agli incastri.

Poiché nel nostro esercizio la struttura è ruotata è più corretto dire che ciò che prima era stato indicato con pilastri ora li identificheremo con travi e viceversa (abbiamo quindi in questo caso dei PILASTRI INFINITAMENTE RIGIDI e delle TRAVI DEFORMABILI). Come abbiamo visto precedentemente la FORZA agente sulla struttura si ripartisce in valori di TAGLIO nei pilastri (in questo caso travi) proporzionali alla loro rigidezza. Essendo quindi le nostre travi di pari luce, materiale e sezione avranno anche la stessa rigidezza.

Ciò comporta che ciascuna trave ha un taglio pari alla metà della forza agente sommata al taglio che proviene dalla trave precedente.

Da tali valori di taglio possiamo ottenere di conseguenza i MOMENTI FLETTENTI moltiplicando il valore del taglio per metà della luce della trave.

$M_{A}=\frac{F}{2}*\frac{l}{2}=\frac{Fl}{4}$ $M_{B}=F*\frac{l}{2}=\frac{Fl}{2}$ $M_{C}=\frac{3}{2}F*\frac{l}{2}=\frac{3}{4}Fl$ $M_{D}=2F*\frac{l}{2}=Fl$

$M_{E}=\frac{5}{2}F*\frac{l}{2}=\frac{5}{4}Fl$ $M_{G}=3F*\frac{l}{2}=\frac{3}{2}Fl$

Possiamo ora analizzare come il momento in ciascun nodo si trasmetta dalla trave al pilastro (grazie all’equilibrio dei momenti nei nodi).

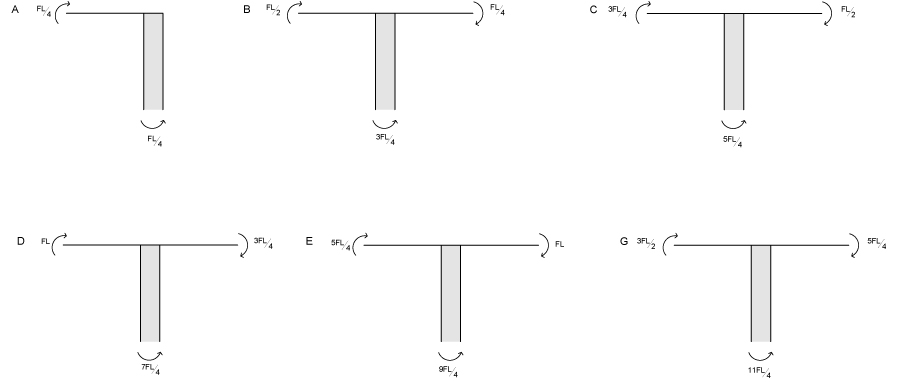
Otteniamo così il seguente diagramma.

Una volta noti i momenti in ciascun pilastro dobbiamo ora ottenere i valori di TAGLIO, per farlo dobbiamo equilibrare a rotazione il pilastri, sommiamo i momenti e dividiamoli per la luce del pilastro.

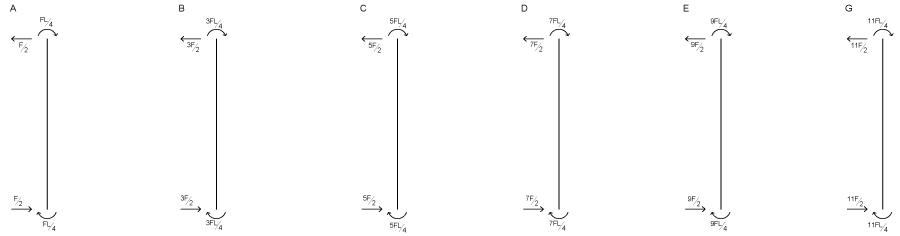
Otteniamo così il seguente diagramma.

Ora rimane da determinare di quanto si deformi ogni campata ovvero a quanto equivale il suo abbassamento (δ), sappiamo che la rigidezza nel telaio shear type simmetrico è pari a 12EI/L³ per ciascuna trave, conoscendo il taglio in ciascuna campata otteniamo:

$\frac{F}{2}=T=\frac{12EI}{l^{3}}\delta_{1} \rightarrow \delta _{1}=\frac{Fl^{3}}{24EI}$

$F=T=\frac{12EI}{l^{3}}\delta_{2} \rightarrow \delta _{2}=\frac{Fl^{3}}{12EI}$

$\frac{3}{2}F=T=\frac{12EI}{l^{3}}\delta_{3} \rightarrow \delta _{3}=\frac{Fl^{3}}{8EI}$

$2F=T=\frac{12EI}{l^{3}}\delta_{4} \rightarrow \delta _{4}=\frac{Fl^{3}}{6EI}$

$\frac{5}{2}F=T=\frac{12EI}{l^{3}}\delta_{5} \rightarrow \delta _{5}=\frac{5Fl^{3}}{24EI}$

$3F=T=\frac{12EI}{l^{3}}\delta_{6} \rightarrow \delta _{6}=\frac{Fl^{3}}{4EI}$

Otteniamo così la seguente DEFORMATA COMPLESSIVA.

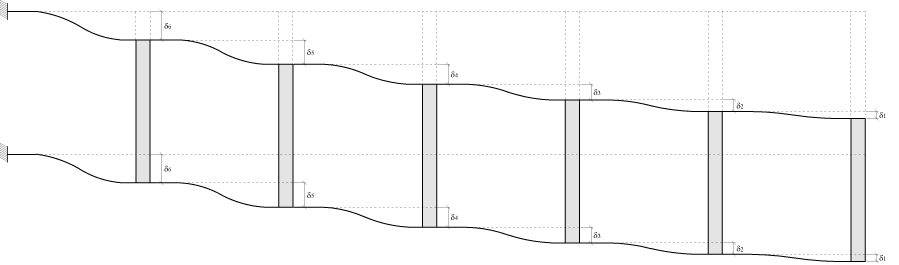
Possiamo ora verificare la struttura in SAP, disegniamo un MODELLO 2D FRAMES identico a quello del nostro esercizio.

L’unica differenza rispetto agli esercizi che sono stati fatti finora è nell’assegnazione dei materiali: dobbiamo infatti assegnare un materiale qualsiasi ed un profilo qualsiasi alle travi, mentre per i pilastri che devono essere INFINITAMENTE RIGIDI possiamo agire sulla sezione (cambiando così il momento d’inerzia) oppure sul materiale (cambiando il modulo elastico). In questo caso si è scelto di assegnare direttamente un modulo elastico “estremamente elevato” ed abbiamo ottenuto così i seguenti diagrammi e deformata.

SFORZO ASSIALE

TAGLIO

MOMENTO

Possiamo notare delle differenze tra il modello ideale ed il risultato ottenuto dalla verifica in SAP. Questo è dovuto al fatto che SAP considera le travi rigide anche se di un valore molto piccolo e di conseguenza il momento nella struttura si distribuisce in maniera diversa. Per ovviare a ciò ed ottenere un risultato il più vicino possibile al modello ideale dobbiamo assegnare alle travi delle sezioni molto piccole o un modulo elastico molto minore, con questa piccola accortezza otteniamo i seguenti risultati.

SFORZO ASSIALE

TAGLIO

MOMENTO

TRAVE VIRENDEEL DOPPIAMENTE INCASTRATA

Anche in questo esercizio possiamo fare riferimento al TEALIO SHEAR TYPE, con la differenza che la struttura questa volta non rimanda ad una mensola bensì ad una trave doppiamente incastrata, visto che abbiamo due incastri anche nel lato destro; questo ci permette di sfruttare il CONCETTO DI SIMMETRIA.

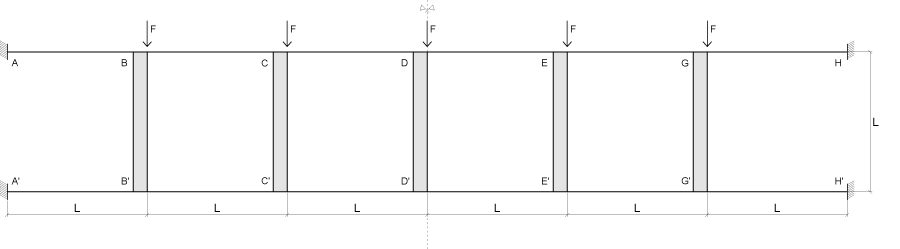
Iniziamo come nell’esercizio precedente calcolando i diversi valori del TAGLIO facendo però attenzione al pilastro centrale dove agisce una forza F/2 a destra e una forza F/2 a sinistra (perché per il concetto di simmetria lo abbiamo immaginato diviso in 2).

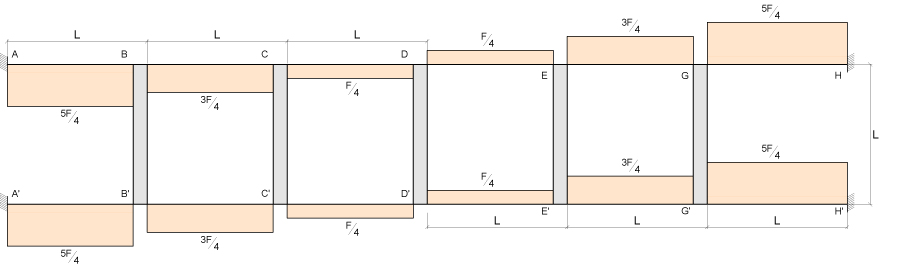
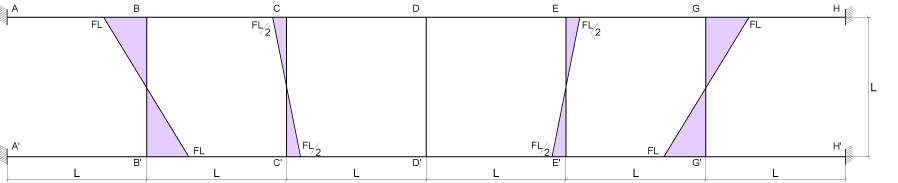
Dai valori del taglio ricaviamo quelli del MOMENTO (sempre moltiplicando il taglio per metà della luce della trave).

$M_{D}=\frac{F}{4}*\frac{l}{2}=\frac{Fl}{8}$ $M_{C}=\frac{3}{4}F*\frac{l}{2}=\frac{3}{8}Fl$ $M_{B}=\frac{5}{4}F*\frac{l}{2}=\frac{5}{8}Fl$

Ora possiamo ottenere i momenti agenti nei pilastri grazie all’equilibrio dei momenti ai nodi, dobbiamo ricordarci di unire il momento del nodo Ds con quello del nodo Dd che precedentemente avevamo considerato separati per poter applicare il concetto di simmetria.

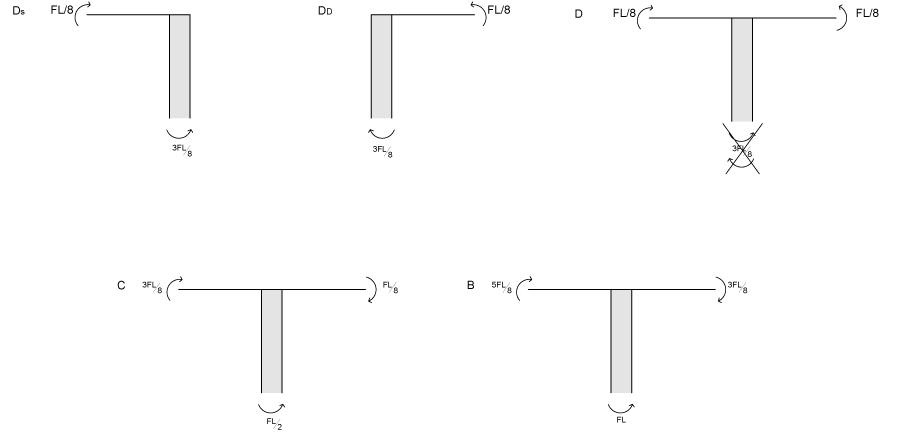
Sempre come nell’esercizio precedente dai valori dei momenti possiamo ricavarci quello del taglio nei pilasti.

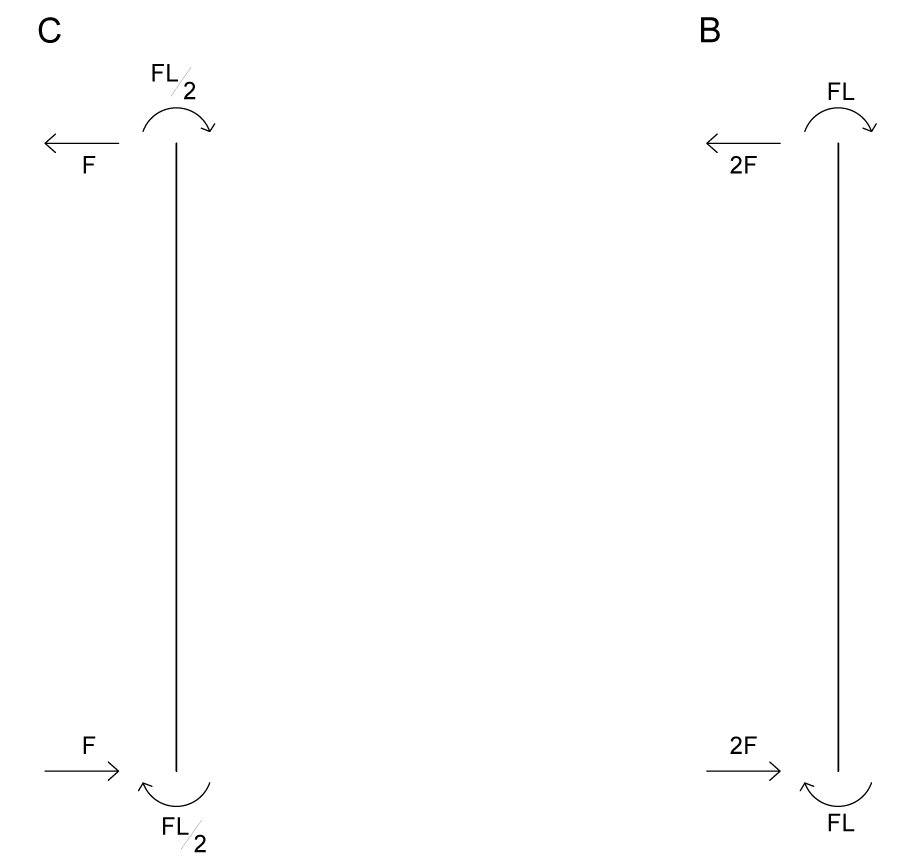
Rimane ora da determinare gli abbassamenti (δ) come abbiamo fatto precedentemente e otteniamo:

$\frac{F}{4}=T=\frac{12EI}{l^{3}}\delta _{1s}\rightarrow \delta _{1s}=\frac{Fl^{3}}{48EI}$

$\frac{3}{4}F=T=\frac{12EI}{l^{3}}\delta _{2}\rightarrow \delta _{2}=\frac{Fl^{3}}{16EI}$

$\frac{5}{4}F=T=\frac{12EI}{l^{3}}\delta _{3}\rightarrow \delta _{3}=\frac{5Fl^{3}}{48EI}$

Otteniamo così la seguente DEFORMATA COMPLESSIVA

Possiamo ora verificare la struttura in SAP, disegnando un MODELLO 2D FRAMES identico a quello del nostro esercizio e ripetendo i passaggi dell’esercizio precedente.

SFORZO ASSIALE

TAGLIO

MOMENTO

SdC(b) (LM PA)

Esercitazione

Blog di lorenzo.procaccini

Menu principale

Tu sei qui

SdC(b)

commenti

Commenti recenti

Maschera di ricerca

ESERCITAZIONE 5_SHEAR TYPE E TRAVE VIRENDEEL