In questa esercirazione andiamo a dimensionare la trave appoggiata più sollecitata di un solaio, dimensionandola a flessione dunque e comparando diversi materiali: acciaio, legno e laterocemento.
Il solaio analizzato è il seguente e mette in evidenza la trave più sollecitata con la sua area d'influenza, ovvero di quale parte del solaio questa si fa carico.

ANALISI DEI CARICHI PER SOLAIO IN ACCIAIO
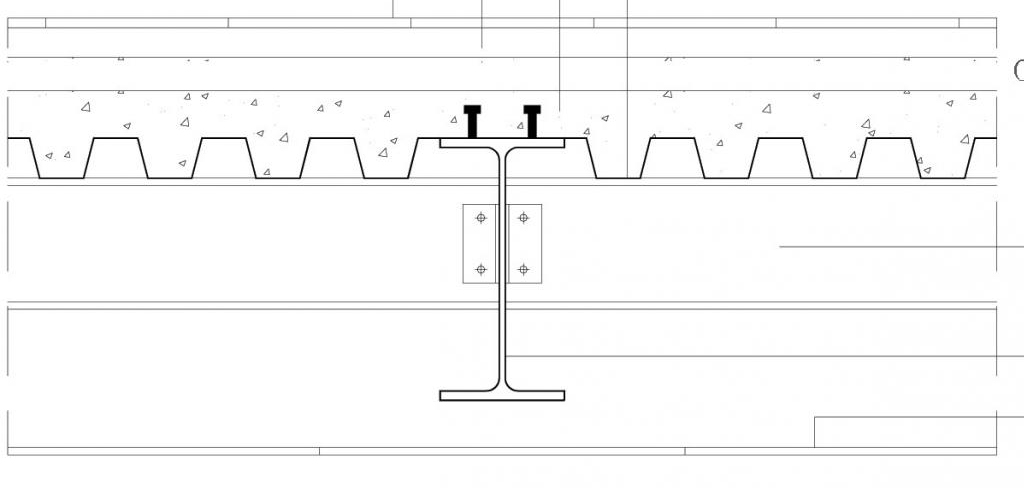
Elementi del Solaio
Lamiera Grecata – spessore: 0.9 mm; altezza: 7 cm; Peso: 0,11 KN/m2
Getto di cls – altezza: 7 cm nella lamiera + 4 cm esterni; Peso Specifico: 25 KN/m3
Isolante – altezza 3 cm; Peso Specifico: 1,8 KN/m3
Massetto – altezza: 5 cm; Peso Specifico: 19 KN/m3
Pavimento – altezza: 3 cm; Peso Specifico: 20 KN/m3
Calcolo Carichi Strutturali
Lamiera Grecata: 0,11 KN/m2
Getto di cls: (25 KN/m3 x 0,04 m) + (25 KN/m3 x 0,07m) / 2 = 1 KN/m2 + 0,875 KN/m2 = 1,875 KN/m2
qs= 0,11 KN/m2 + 1,875 KN/m2 = 1,985 KN/m2
Calcolo Carichi Permanenti
Isolante: 1,8 KN/m3 x 0,03m = 0,054 KN/m2
Massetto: 19 KN/m3 x 0,05 m = 0,95 KN/m2
Pavimento: 20 KN/m3 x 0,03 m = 0,6 KN/m2
Tramezzi: 1 KN/m2
Impianti: 0,5 KN/m2
qp= 0,054 KN/m2 + 0,95 KN/m2 + 0,6 KN/m2 + 1 KN/m2 + 0,5 KN/m2 = 3,104 KN/m2
Calcolo Carichi Accidentali
I carichi accidentali sono dati dalla normativa: essendo ad uso residenziale abbiamo che
qa = 2 KN/m2
DIMENSIONAMENTO A FLESSIONE
Una volta trovati tutti i carichi inserisco nella tabella excel del dimensionamento a flessione (nella sezione acciaio) i valori dei carichi ricavati, l'interasse, la luce della trave e scelgo una classe di acciaio (S275), in modo che moltiplicando i carichi per i loro coefficenti di sicurezza, moltiplicandoli per l'interasse e sommandoli, ottengo il mio carico ripartito sulla trave qu.
So che il Momento massimo di una trave appoggiata sottoposta a un carico ripartito equivale a qL2/8; sapendo tutti i valori lo calcolo e grazie a questo mi trovo il Wx min (=Mmax/fyd).

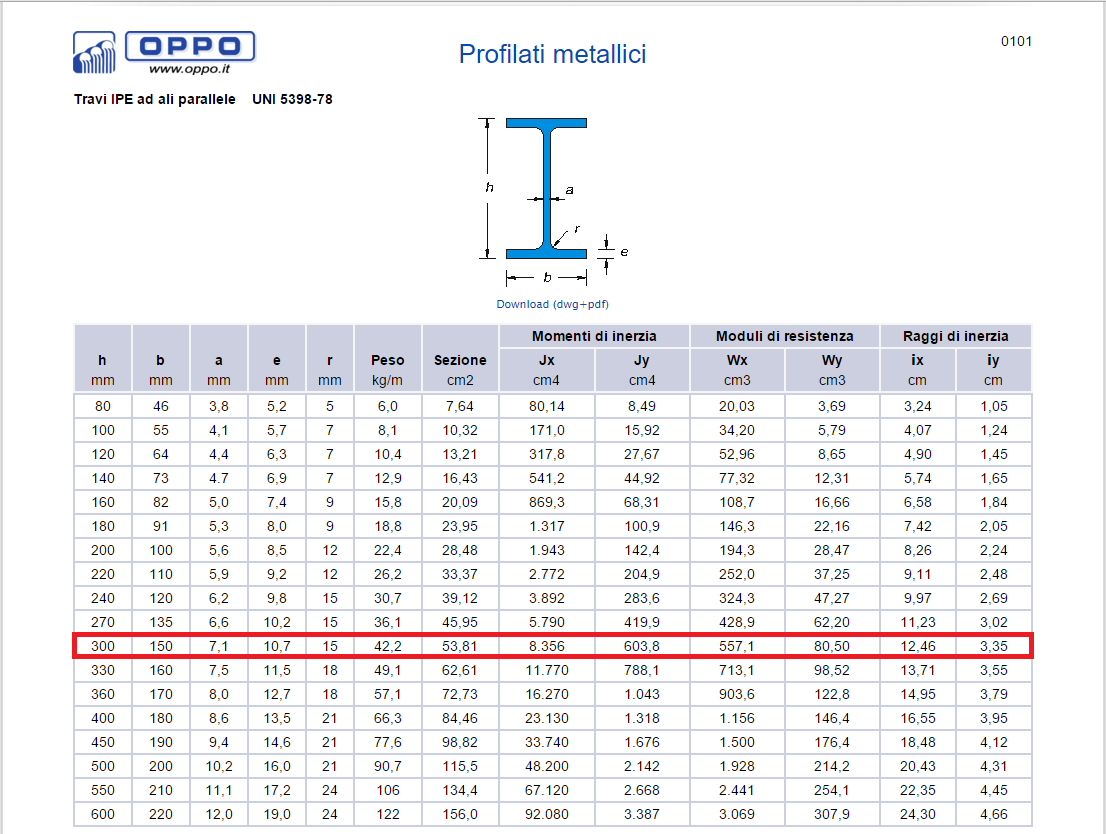
Grazie a questo valore trovo un profilato industralizzato adeguato, ovvero con un Wx > Wx min: una IPE300
ANALISI DEI CARICHI PER SOLAIO IN LATEROCEMENTO
Elementi del Solaio
Calcestruzzo armato – altezza: 5 cm + 25x10 cm dei travetti; Peso Specifico: 25 KN/m3
Pignatte – 12x50x25 cm; Peso: 1,05 KN/m2 con travetti di interasse 60 cm
Isolante – altezza 3 cm; Peso Specifico: 1,8 KN/m3
Massetto – 5 cm; Peso Specifico: 19 KN/m3
Pavimento – 3 cm; Peso Specifico: 20 KN/m3
Calcolo Carichi Strutturali
Cls armato: 25 KN/m3 x 0,05m + [(0,025 m3 x 2) x 25 KN/m3] / m2 = 1,25 KN/m2 + 1,25 KN/m2 = 2,5 KN/m2
Pignatte: 1,05 KN/m2
qs= 2,5 KN/m2 + 1,05 KN/m2 = 3,55 KN/m2
Calcolo Carichi Permanenti
Isolante: 1,8 KN/m3 x 0,03m = 0,054 KN/m2
Massetto: 19 KN/m3 x 0,05 m = 0,95 KN/m2
Pavimento: 20 KN/m3 x 0,03 m = 0,6 KN/m2
Tramezzi: 1 KN/m2
Impianti: 0,5 KN/m2
qp= 0,054 KN/m2 + 0,95 KN/m2 + 0,6 KN/m2 + 1 KN/m2 + 0,5 KN/m2 = 3,104 KN/m2
Calcolo Carichi Accidentali
I carichi accidentali sono dati dalla normativa: essendo ad uso residenziale abbiamo che
qa = 2 KN/m2
DIMENSIONAMENTO A FLESSIONE
Trovo qu nuovamente grazie ai carichi, i coefficenti e l'interasse e di conseguenza il Momento massimo. Inserisco le tensioni caratteristiche fk di cls e acciaio (C60 e S450) e trovo le tensioni caratteristiche di progetto fcd e fyd grazie ai coefficenti.
A questo punto scelgo una dimensione per la base della mia trave (25 cm) e per il mio copriferro (5 cm) e grazie alla tabella excel ottengo un'altezza minima di 34,14 cm, dunque inizialmente ho scelto una trave 25x35 cm, in seguito però analizzando il carico con aggiunta del peso proprio, la trave non era verificata e l'altezza minima era di 35,4 cm, dunque ho scelto una trave 25x40 cm, in questo modo la sezione risulta verificata.

ANALISI DEI CARICHI PER SOLAIO IN LEGNO
Elementi del Solaio
Travetti – altezza: 10x20cm con 50cm di interasse; Peso Specifico: 4 KN/m3 (abete rosso)
Tavolato – altezza: 3 cm; Peso Specifico: 4 KN/m3 (abete rosso)
Isolante – altezza 3 cm; Peso Specifico: 1,8 KN/m3
Massetto – 5 cm; Peso Specifico: 19 KN/m3
Pavimento – 3 cm; Peso Specifico: 20 KN/m3
Calcolo Carichi Strutturali
Travetti: [(0,02 m3 x 2) x 4 KN/m3] / m2 = 0,16 KN/m2
Tavolato: 4 KN/m3 x 0,03 m = 0,12 KN/m2
qs= 0,16 KN/m2 + 0,12 KN/m2 = 0,28 KN/m2
Calcolo Carichi Permanenti
Isolante: 1,8 KN/m3 x 0,03m = 0,054 KN/m2
Massetto: 19 KN/m3 x 0,05 m = 0,95 KN/m2
Pavimento: 20 KN/m3 x 0,03 m = 0,6 KN/m2
Tramezzi: 1 KN/m2
Impianti: 0,5 KN/m2
qp= 0,054 KN/m2 + 0,95 KN/m2 + 0,6 KN/m2 + 1 KN/m2 + 0,5 KN/m2 = 3,104 KN/m2
Calcolo Carichi Accidentali
I carichi accidentali sono dati dalla normativa: essendo ad uso residenziale abbiamo che
qa = 2 KN/m2
DIMENSIONAMENTO A FLESSIONE
Nuovamente, trovati i diversi carichi trovo il carico distribuito qu e calcolo il Momento massimo. A questo punto inserisco la tensione caratteristica del materiale da me scelto (Abete rosso) fmk = 24 MPa, che moltiplicato per il fattore di umidità kmod e diviso per il coefficente di sicurezza dà la tensione caratteristica di progetto fmd.
Fatto questo scelgo un valore per la mia base, scegliendo tra i valori industrializzati (24 cm), trovo un'altezza minima pari a 45,21 cm, dunque scelgo un profilato 24x48 cm (sempre controllando tra i valori industrializzati).

Commenti recenti