ESERCITAZIONE 4 - Centro delle Rigidezze e Ripartizioni delle Forze Sismiche

In questa esercitazione andremo a calcolare come si ripartiscono le forze orizzontali (sismiche o causate dal vento) che agiscono su di un impalcato, andando ad analizzare le rigidezze dei suoi controventi, trovandone il centro di massa ed il centro delle rigidezze e calcolando gli spostamenti e la rotazione subiti dall'impalcato stesso.

 

L'impalcato proposto è un telaio in cemento armato assimilabile al comportamento di un telaio shear-type.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

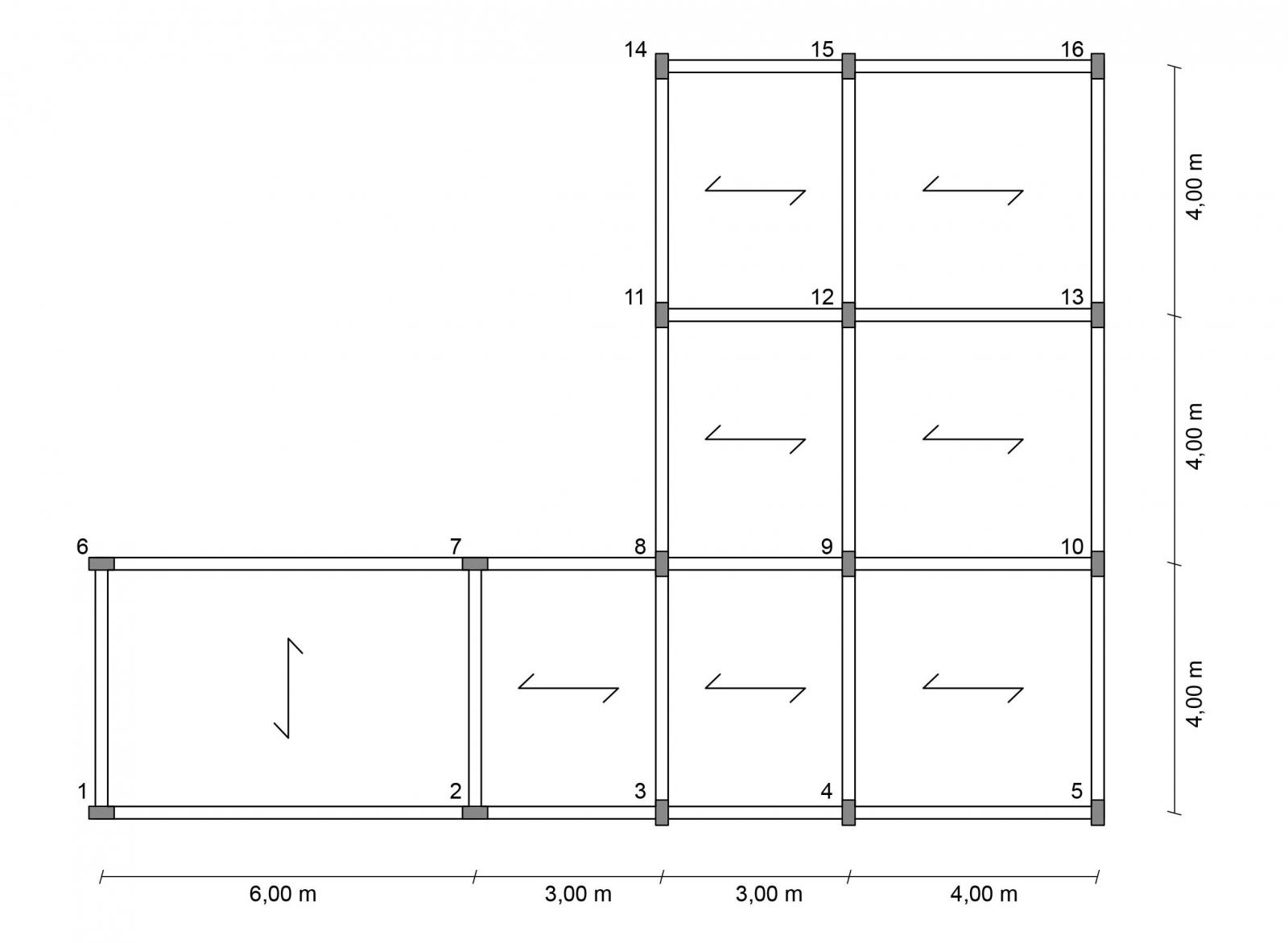
Identifichiamo quindi tutti i telai che hanno funzione di controventamento, orizzontalmente e verticalmente:

T1v - pilastri 1-6                                    T1o - pilastri 1-2-3-4-5

T2v - pilastri 2-7                                    T2o - pilastri 6-7-8-9-10

T3v - pilastri 3-8-11-14                           T3o - pilastri 11-12-13

T4v - pilastri 4-9-12-15                           T4o - pilastri 14-15-16

T5v - pilastri 5-10-13-16

 

I controventi possono essere idealmente rappresentati come delle molle in quanto rappresentano dei vincoli cedevoli elasticamente dell'impalcato, piochè permettono uno spostamento elastico.

 

 

 

 

 

 

 

 

 

 

 

 

 

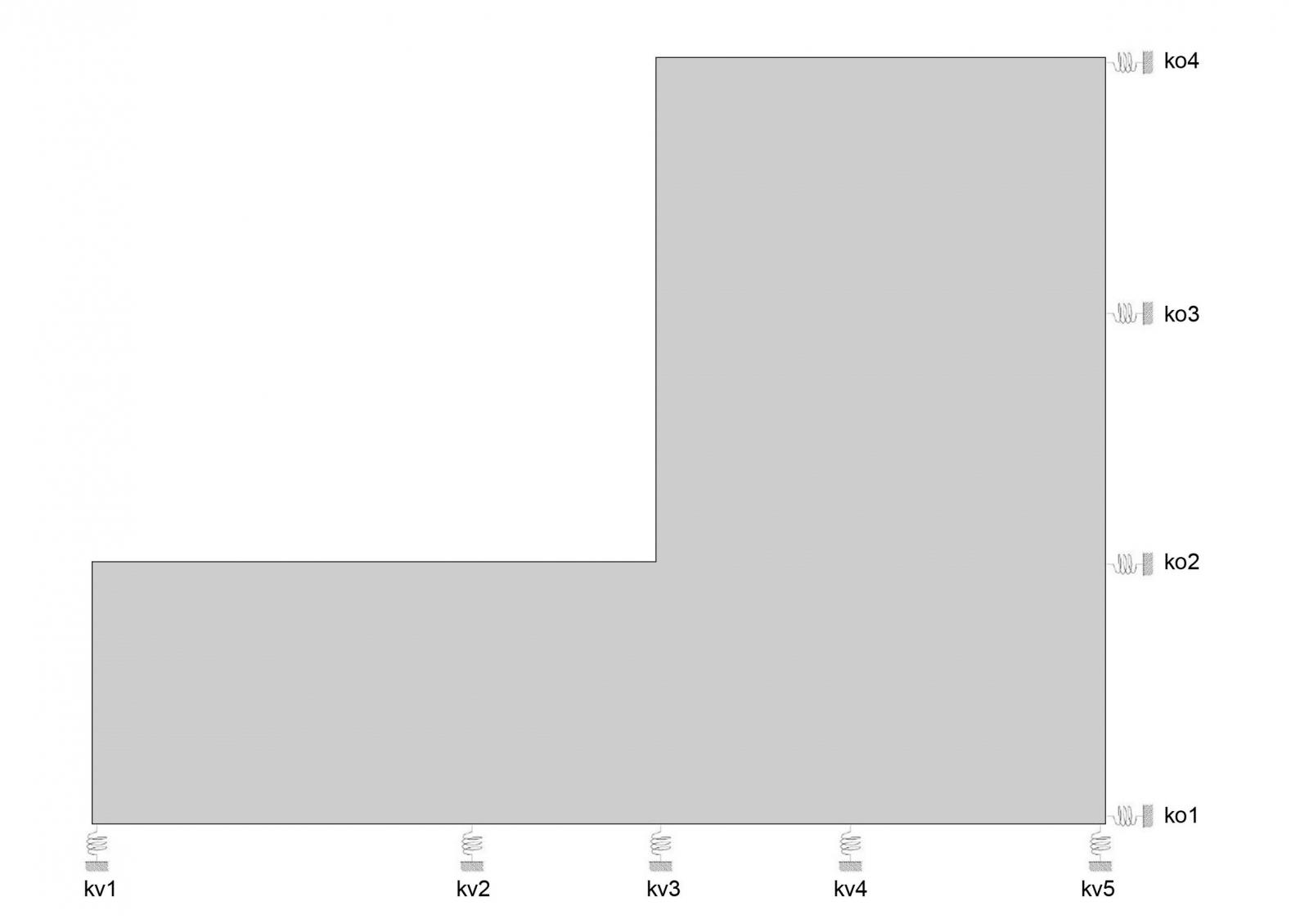
Avendo inoltre detto che il telaio dell'impalcato è assimilabbile ad un modello shear-type, e sapendo che la rigidezza dei pilastri di tale telaio è k = 12EI / h³, possiamo calcolare la rigidezza k dei controventi come somma delle rigidezze dei pilastri che li compongono:

 

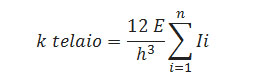
ad esempio:     kv1 = (12E / h³) x (I₁ + I₆)

con E, modulo di Young o modulo elastico = 21000 Mpa

      H, altezza del pilastro = 3,5 m

      I, momento d'inerzia del pilastro a sezione rettangolare = b x h³ / 12 che con dei pilastri 20x40 cm ho che

 

 

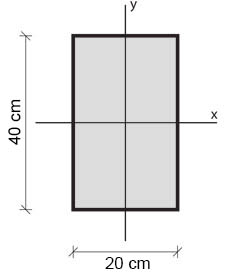
       I_y = 26666,67 cm⁴

 

       I_x = 106666,67 cm⁴

 

 

 

Ultilizzando la tabella excel (aggiungendo parti e modificando altre del file scaricabile dal sito) ottengo facilmente i valori delle rigidezze k dei controventi.

Fatto ciò raccolgo in una tabella le rigidezze dei vari controventi e la rispettive distanze da un punto d'origine O, da me posto sul pilastro 1.

 

 

 

 

 

 

 

 

 

Trovo il centro di massa dell'impalcato suddividendolo il due geometrie semplici (due rettangoli) e utilizzo la formula dei centri adattandola per il centro di massa

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

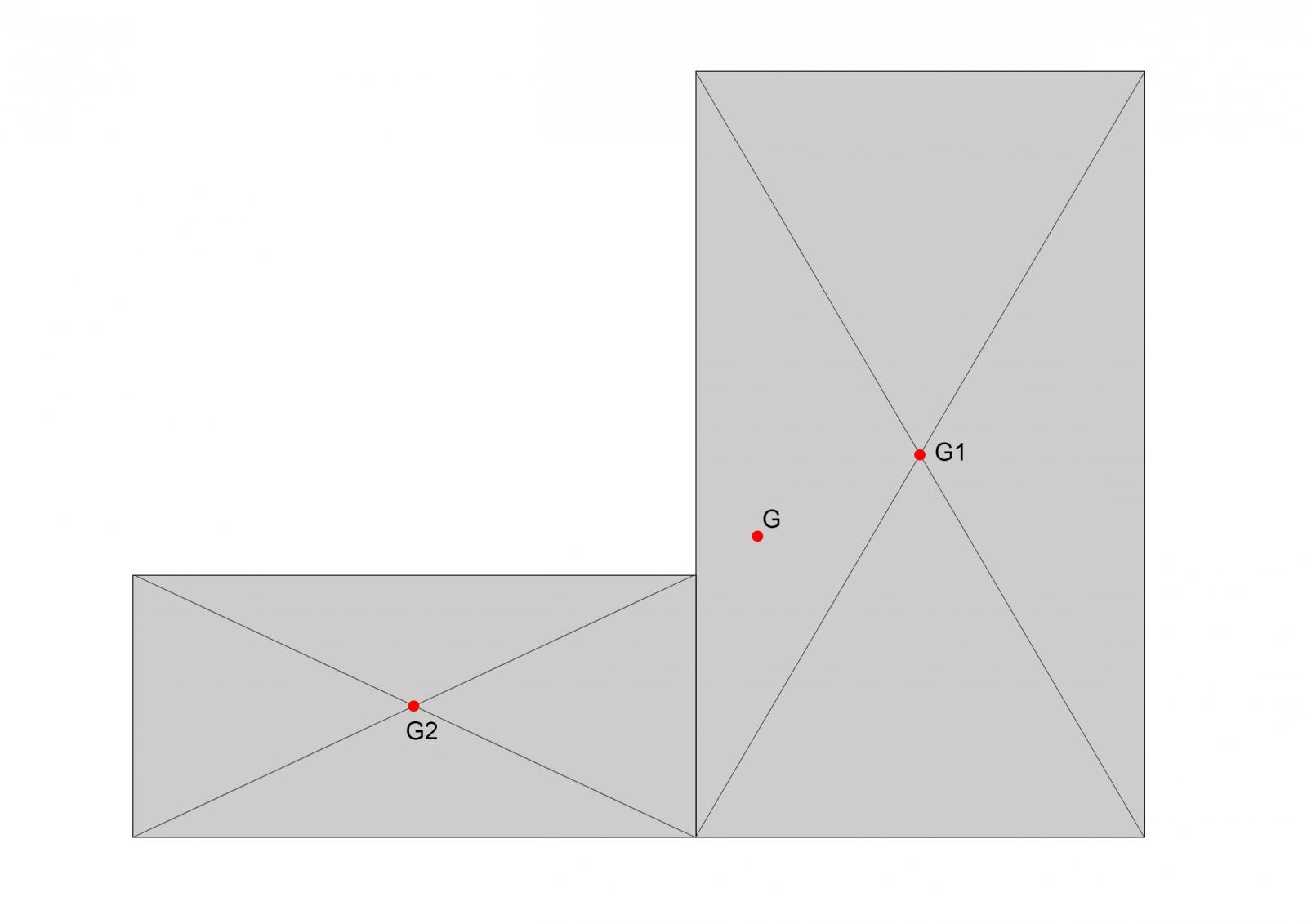
Una volta trovato il centro di massa trovo il centro delle rigidezze con la stessa formula precedente dei centri ma adattata per il centro delle rigidezze

 

 

 

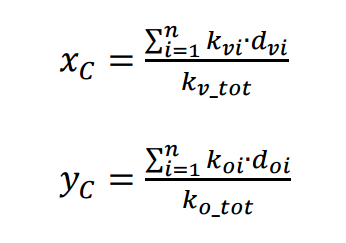
trovo a questo punto anche la rigidezza totale orizzontale, verticale e torsionale dell'impalcato

 

 

 

 

 

 

 

Vediamo dunque il centro di massa e quello delle rigidezze a confronto

 

 

 

 

 

 

 

 

 

 

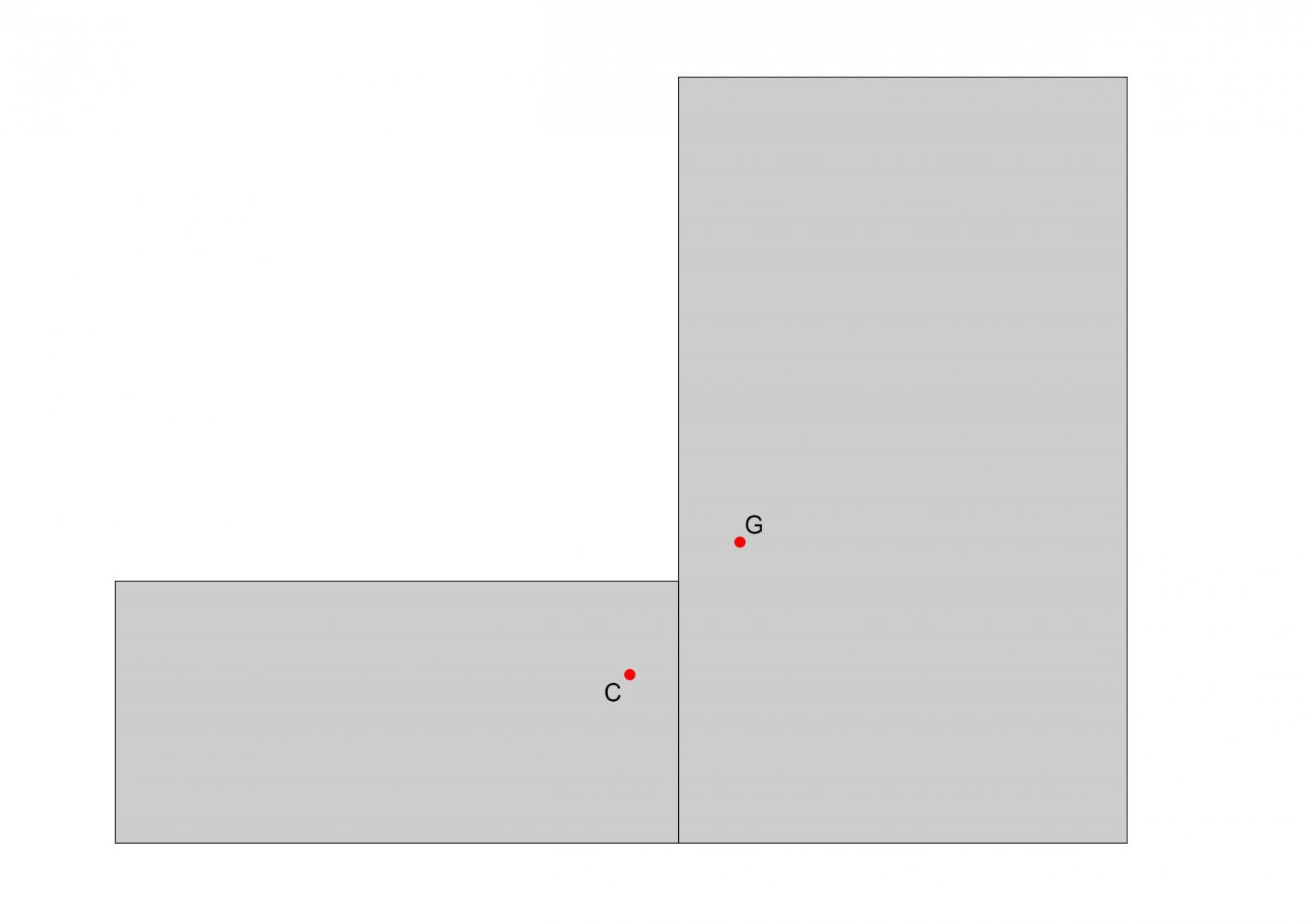
Il fatto che il centro delle rigidezze sia così distante dal centro di massa avrà ripercussioni negative sull'edificio in quanto la forze orizzontali (sia lungo x che lungo y), che agiscono in G, avranno un braccio e dunque provocheranno una rotazione dell'edificio. Sarebbe buona norma riprogettare i controventi in modo da dare maggiore rigidezza nel lato destro e superiore dell'impalcato così da avvicinare il centro delle rigidezze C il più possibile al centro di massa G.

 

Ora andiamo a calcolare il peso dell'impalcato allo SLE, che possiamo identificare come peso sismico W e lo moltiplichiamo per un coefficente c = 0,1, coefficente di intensità sismica che varia a seconda della zona in cui si trova l'impalcato. Così otteniamo la Forza sismica orizzontale.

 

 

 

 

 

La forza sismica quindi la andiamo ad applicare nel centro di massa dell'impalcato prima orizzontalmente (lungo x) e poi verticalmente (lungo y). Avremo quindi che la forza applicata in direzione x comporterà rotazione e traslazione orizzontale dell’impalcato mentre la forza applicata in direzione y comporterà rotazione e traslazione verticale dell’impalcato

Troviamo così lo spostamento orizzontale u = F / k_{o_tot} e lo spostamento verticale v = F / k_{v_tot}

La rotazione φ = M_c / kφ

Dove M_c è il momentro torcente dato dal prodotto tra forsa simica F ed il braccio, ovvero la distanza tra G e C (distanza lungo x e lungo y ovviamente).

 

Possiamo infine ricavarci la forza sui singoli controventi nei due casi di carico.

Quando la forza è applicata in direzione x

la reazione elastica dei controventi orizzontali è pari a F_{o_n} = k_{o_n} (u + φ dd_{o_n})

Mentre nei vericali è F_{v_n} = k_{v_n} φ dd_{v_n}

 

Quando la forza è applicata in direzione y

la reazione elastica dei controventi verticali è pari a F_{v_n} = k_{v_n} (v + φ dd_{v_n})

Mentre negli orizzontali è F_{o_n} = k_{o_n} φ dd_{o_n}